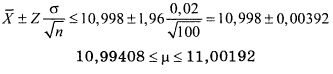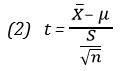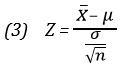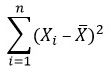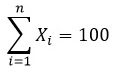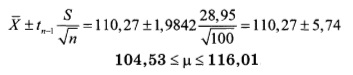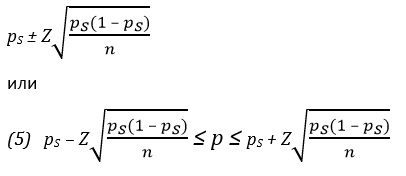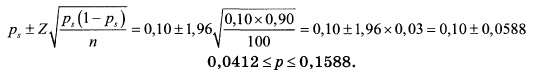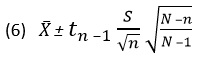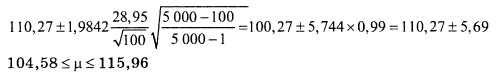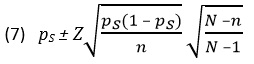В статистике существует два вида оценок: точечные и интервальные. Точечная оценка представляет собой отдельную выборочную статистику, которая используется для оценки параметра генеральной совокупности.[1] Например, выборочное среднее ![]() — это точечная оценка математического ожидания генеральной совокупности, а выборочная дисперсия S2 — точечная оценка дисперсии генеральной совокупности σ2. Ранее было показано, что выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности. Выборочное среднее называется несмещенным, поскольку среднее значение всех выборочных средних (при одном и том же объеме выборки n) равно математическому ожиданию генеральной совокупности.
— это точечная оценка математического ожидания генеральной совокупности, а выборочная дисперсия S2 — точечная оценка дисперсии генеральной совокупности σ2. Ранее было показано, что выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности. Выборочное среднее называется несмещенным, поскольку среднее значение всех выборочных средних (при одном и том же объеме выборки n) равно математическому ожиданию генеральной совокупности.
Для того чтобы выборочная дисперсия S2 стала несмещенной оценкой дисперсии генеральной совокупности σ2, знаменатель выборочной дисперсии следует положить равным n – 1, а не n. Иначе говоря, дисперсия генеральной совокупности является средним значением всевозможных выборочных дисперсий.
При оценке параметров генеральной совокупности следует иметь в виду, что выборочные статистики, такие как ![]() , зависят от конкретных выборок. Чтобы учесть этот факт, для получения интервальной оценки математического ожидания генеральной совокупности анализируют распределение выборочных средних (подробнее см. Выборочные распределения). Построенный интервал характеризуется определенным доверительным уровнем, который представляет собой вероятность того, что истинный параметр генеральной совокупности оценен правильно. Аналогичные доверительные интервалы можно применять для оценки доли признака р и основной распределенной массы генеральной совокупности.
, зависят от конкретных выборок. Чтобы учесть этот факт, для получения интервальной оценки математического ожидания генеральной совокупности анализируют распределение выборочных средних (подробнее см. Выборочные распределения). Построенный интервал характеризуется определенным доверительным уровнем, который представляет собой вероятность того, что истинный параметр генеральной совокупности оценен правильно. Аналогичные доверительные интервалы можно применять для оценки доли признака р и основной распределенной массы генеральной совокупности.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении
Ранее мы применили информацию о распределении и центральную предельную теорему, [2] чтобы вычислить процентную долю выборочных средних, лежащих в окрестности математического ожидания генеральной совокупности на расстоянии, не превышающем заданное. Например, при анализе веса коробок с кукурузными хлопьями, 95% всех выборочных средних лежат в интервале от 362,12 до 373,88 г. Это утверждение получено с помощью дедукции, поскольку свойства выборки определялись на основе данных о генеральной совокупности. Однако теперь нам необходимо применить противоположный способ рассуждения — индуктивный, так как в теории статистического вывода, наоборот, свойства генеральной совокупности определяются на основе параметров отдельной выборки. На практике математическое ожидание генеральной совокупности, как правило, не известно и должно быть оценено. Вернемся к примеру с коробками. Допустим теперь, что математическое ожидание генеральной совокупности μ не известно, а истинное стандартное отклонение генеральной совокупности σ равно 15 г. Тогда в формулах для определения границ интервала μ ± 1,96σ/√n математическое ожидание генеральной совокупности μ следует заменить выборочным средним ![]() . Следовательно, для оценки неизвестного математического ожидания генеральной совокупности можно применить интервал
. Следовательно, для оценки неизвестного математического ожидания генеральной совокупности можно применить интервал ![]() ± 1,96σ/√n. На практике, как правило, из генеральной совокупности извлекают выборку фиксированного объема n и вычисляют выборочное среднее
± 1,96σ/√n. На практике, как правило, из генеральной совокупности извлекают выборку фиксированного объема n и вычисляют выборочное среднее ![]() . Однако, чтобы понять смысл интервальной оценки, необходимо рассмотреть гипотетическое множество всех возможных выборок данного объема.
. Однако, чтобы понять смысл интервальной оценки, необходимо рассмотреть гипотетическое множество всех возможных выборок данного объема.
Допустим, например, что математическое ожидание генеральной совокупности μ равно 368 г. Предположим, что из генеральной совокупности коробок извлекается выборка, состоящая из 25 коробок, средний вес которых равен 362,3 г. Интервал, предложенный для оценки математического ожидания μ, имеет границы: 362,3 ± 1,96×15/√25 = 362,3 ± 5,88. Таким образом, 356,42 < μ < 368,18.
Поскольку математическое ожидание генеральной совокупности μ равно 368, оно попадает в этот интервал, и, следовательно, данная выборка позволяет правильно ее оценить (рис. 1).
Рис. 1. Доверительные интервальные оценки математического ожидания генеральной совокупности, полученные по пяти разным выборкам объема n = 25, извлеченным из генеральной совокупности с параметрами μ = 368 и σ = 15
Допустим, что выборочное среднее некоей выборки объема n = 25, равно 369,5. Доверительный интервал, построенный по этой выборке, имеет границы, равные 369,5 ± 1,96×15/√25 , т.е. 369,5 ± 5,9. Таким образом, 363,62 < μ < 375,38. Поскольку математическое ожидание генеральной совокупности μ равно 368, оно попадает в этот интервал, и, следовательно, данная оценка является правильной. Возникает впечатление, что выборки, имеющие объем n = 25, всегда приводят к правильным оценкам математического ожидания генеральной совокупности μ. Чтобы опровергнуть это, рассмотрим третий гипотетический пример. Допустим, что средний вес коробок равен 360 г. Интервал, предложенный для оценки математического ожидания μ, имеет границы: 360 ± 1,96×15/√25 , т.е. 360 ± 5,88. Таким образом, в данном случае 354,12 < μ < 365,88. Эта оценка неверна, поскольку математическое ожидание генеральной совокупности μ равно 368 и не попадает в этот интервал (см. рис. 1). Таким образом, для некоторых выборок эта оценка верна, а для некоторых — нет. Кроме того, на практике, из генеральной совокупности извлекается только одна выборка. Следовательно, поскольку математическое ожидание генеральной совокупности μ не известно, невозможно сказать, верна полученная интервальная оценка или нет.
Чтобы разрешить эту дилемму, необходимо определить долю выборок, позволяющих правильно оценить математическое ожидание генеральной совокупности μ. Для этого следует исследовать еще две гипотетические выборки, средние значения которых равны 362,12 и 373,88 г соответственно. Если ![]() = 362,12, мы получаем интервал 362,12 ±1,96×15/√25 , т.е. 362,12 ± 5,88. Это приводит к оценке 356,24 < μ < 368,00. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является верхней границей интервала, эта оценка верна. Если
= 362,12, мы получаем интервал 362,12 ±1,96×15/√25 , т.е. 362,12 ± 5,88. Это приводит к оценке 356,24 < μ < 368,00. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является верхней границей интервала, эта оценка верна. Если ![]() = 373,88, мы получаем интервал 373,88 ± 1,96×15/√25 , т.е. 373,88 ± 5,88. Это приводит к оценке 368,00 < μ < 379,76. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является нижней границей интервала, эта оценка верна.
= 373,88, мы получаем интервал 373,88 ± 1,96×15/√25 , т.е. 373,88 ± 5,88. Это приводит к оценке 368,00 < μ < 379,76. Поскольку математическое ожидание генеральной совокупности μ, равное 368, является нижней границей интервала, эта оценка верна.
Таким образом, если выборочное среднее изменяется в диапазоне от 362,12 до 373,88 г, математическое ожидание генеральной совокупности лежит где-то внутри этого соответствующего доверительного интервала. Вероятность того, что это значение лежит в интервале с границами 362,12 и 373,88, равна 95% (об этом говорилось в начале раздела). Следовательно, 95% средних значений всех выборок, имеющих объем n = 25, позволяют правильно оценить математическое ожидание генеральной совокупности, а 5% — нет.
Интервальная оценка, доверительный уровень которой равен 95%, интерпретируется следующим образом: если из генеральной совокупности извлечь все выборки, имеющие объем n, и вычислить их выборочные средние, то 95% доверительных интервалов, построенных на их основе, будут содержать математическое ожидание генеральной совокупности, а 5% — нет. На практике, как правило, из генеральной совокупности извлекается только одна выборка, а математическое ожидание генеральной совокупности μ не известно. По этой причине невозможно гарантировать, что некий конкретный доверительный интервал содержит величину μ. Можно лишь утверждать, что вероятность этого события равна 95%.
В некоторых ситуациях желательно иметь более высокий доверительный уровень, а следовательно, точность оценки величины μ (например, 99%). Но иногда можно ограничиться и менее точной оценкой (например, 90%).
Как правило, доверительный уровень обозначают следующим образом: (1 – α)х100%, где величина α представляет собой площадь, ограниченную хвостом распределения, выходящим за пределы доверительного интервала. (Величину α называют уровнем значимости доверительного интервала. Кроме того, в качестве синонима для доверительного уровня иногда употребляется выражение «доверительная вероятность».) Площади, ограниченные как левым, так и правым хвостами распределения, выходящими за пределы доверительного интервала, равны α/2.
Построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении
где Z — значение стандартизованной нормально распределенной случайной величины, соответствующее интегральной вероятности, равной 1 – α/2, σ — стандартное отклонение генеральной совокупности.
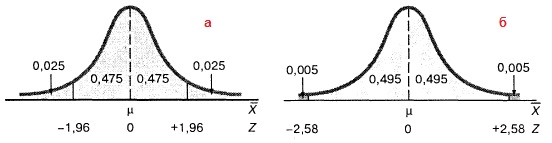
Величина Z, выбранная для построения доверительного интервала, называется критическим значением распределения. Чтобы построить интервал, имеющий 95%-ный доверительный уровень, необходимо выбрать α = 0,05. Половина площади симметричной фигуры, ограниченной концами доверительного интервала и кривой стандартизованного нормального распределения, равна 0,95/2=0,475. Величина Z, соответствующая площади 0,4750, равна 1,96, поскольку площадь фигуры, ограниченной правым хвостом распределения, равна 0,025, а суммарная площадь фигуры, лежащей левее значения Z = 1,96, равна 0,975.
Каждому доверительному уровню 1 – α соответствует свое критическое значение. Например, доверительному уровню, равному 95%, соответствует Z = ±1,96 (рис. 2а). Если требуется построить интервал, доверительный уровень которого равен 99%, следует выбрать α = 0,01. В этом случае величина Z приближенно равна 2,58, поскольку площадь, ограниченная правым хвостом распределения, выходящим за пределы доверительного интервала, равна 0,005, а суммарная площадь фигуры, лежащей левее значения Z, равна 0,995 (рис. 2б).
Рис. 2. Гауссова кривая для определения критического значения Z, соответствующего доверительному уровню, равному: (а) 95%; (б) 99%
Возникает вопрос, почему бы не построить интервал, доверительный уровень которого был бы очень близок к 100%. Это нецелесообразно, поскольку такой доверительный интервал оказался бы слишком широким, а оценка математического ожидания — слишком неточной. Разумеется, вероятность того, что математическое ожидание лежит в этом интервале, очень высока, однако для принятия решения этот факт практически бесполезен.
Пример 1. При производстве бумаги средняя длина листа должна быть равной 11 дюймам, а ее стандартное отклонение — 0,02 дюйма. Периодически из произведенной продукции, чтобы оценить ее качество, извлекаются выборки. Допустим, выборка состоит из 100 листов, а ее выборочное среднее — 10,998 дюйма. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%.
Решение. Подставим в формулу (1) величину Z = 1,96, соответствующую доверительному уровню, равному 95%:
Таким образом, вероятность того, что математическое ожидание генеральной совокупности лежит в интервале от 10,99408 до 11,00192, равна 95%. [3] Поскольку номинальная длина бумаги — 11 дюймов, она попадает в построенный интервал. Следовательно, производственный процесс выполняется правильно.
В Excel до версии 2007 используется функция =ДОВЕРИТ(), начиная с версии 2010 =ДОВЕРИТ.НОРМ(), возвращающая доверительный интервал для среднего генеральной совокупности с использованием нормального распределения. Для приведенного выше примера 1 вычисления в Excel показаны на рис. 3.
Рис. 3. Расчет доверительного интервал для среднего генеральной совокупности в Excel
Построение доверительного интервала для математического ожидания генеральной совокупности при неизвестной дисперсии
На практике как математическое значение генеральной совокупности, так и его стандартное отклонение часто бывают неизвестными. Следовательно, необходимо построить доверительный интервал, содержащий математическое значение генеральной совокупности, используя лишь выборочные статистики ![]() и S.
и S.
В начале 20-го века статистик Уильям С. Госсет, сотрудник ирландского отделения пивоваренной компании Guinness, заинтересовался проблемой оценки математического ожидания при неизвестном стандартном отклонении. Поскольку компания Guinness запрещала своим сотрудникам публиковать работы под собственными именами, Госсет взял псевдоним Стьюдент. По этой причине распределение, предложенное Госсетом, называется t-распределением Стьюдента. Если случайная величина ![]() является нормально распределенной, то следующая статистика имеет t-распределение с n – 1 степенями свободы (о степенях свободы см. ниже):
является нормально распределенной, то следующая статистика имеет t-распределение с n – 1 степенями свободы (о степенях свободы см. ниже):
Обратите внимание на то, что это выражение почти совпадает с формулой (3) определения величины Z для выборочного распределения средних, только вместо величины σ в нем стоит выборочное стандартное отклонение S:
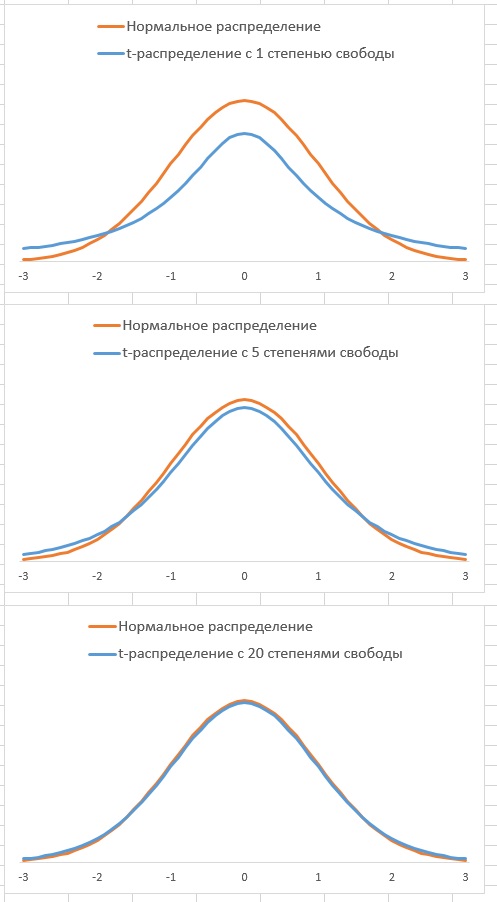
Внешне распределение Стьюдента очень напоминает стандартизованное нормальное распределение (рис. 4).
Рис. 4. Стандартизованное нормальное распределение и t-распределение Стьюдента с различным числом степеней свободы
Оба распределения имеют колоколообразную форму и являются симметричными. Однако хвосты t-распределения «тяжелее» (т.е. ограничивают большую площадь), а площадь фигуры в центре определения меньше, чем у стандартизованного нормального распределения. Это происходит потому, что стандартное отклонение σ не известно, а вместо него используется его выборочная оценка S. Неопределенность значения σ порождает большую изменчивость переменной t по сравнению с величиной Z. Однако при увеличении количества степеней свободы t-распределение становится все ближе к стандартизованному нормальному распределению. Это происходит потому, что при увеличении объема выборки оценка S становится все точнее. При объеме выборки, равном 120 и более, величина S довольно точно аппроксимирует стандартное отклонение σ, так что разница между t-распределением и стандартизованным нормальным отклонением становится минимальной. По этой причине, если объем выборки превышает 120, многие статистики вместо величины t используют переменную Z.
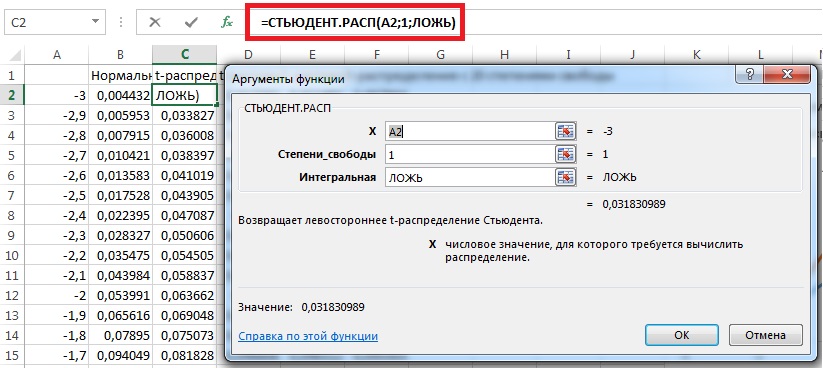
Для построения в Excel графиков t-распределения Стьюдента, начиная с версии 2010 используется функция =СТЬЮДЕНТ.РАСП() (рис. 5). В Excel более ранних версий используется функция =СТЬЮДРАСП(). При этом следует иметь ввиду, что только начиная с версии 2010 с использованием функции =СТЬЮДЕНТ.РАСП() можно построить t-распределения Стьюдента, как для положительных, так и отрицательных значений без дополнительных не вполне очевидных манипуляций…
Рис. 5. Функция Excel =СТЬЮДЕНТ.РАСП() для построения плотности вероятности
Проверка предположений. Напомним, что t-распределение основано на предположении, что изучаемая случайная величина X является нормально распределенной. Однако на практике t-распределение можно применять для оценки неизвестного математического ожидания генеральной совокупности при неизвестном стандартном отклонении при достаточно большом объеме выборки и не слишком асимметричном распределении. При работе с небольшими выборками эти условия уже не выполняются автоматически, поэтому их следует проверять. Для этого необходимо строить гистограмму, диаграмму «ствол и листья», блочную диаграмму или график нормального распределения.
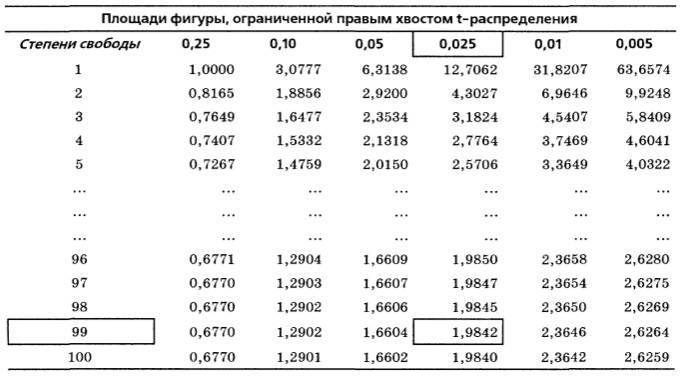
Критические значения для t-распределения с соответствующими степенями свободы можно найти в таблице (рис. 6). В заголовке каждого столбца этой таблицы указана площадь фигуры, ограниченной хвостом t-распределения (поскольку для переменной t указаны только положительные значения, эта площадь ограничена правым хвостом распределения). В заголовке каждой строки указано количество степеней свободы.
Рис. 6. Определение площади фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t
Например, на рис. 6 показано, как найти площадь фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t, если необходимо построить интервал, доверительный уровень которого равен 95%. Этот доверительный уровень означает, что площадь каждой фигуры, ограниченной хвостами t-распределения, равна 0,025. Найдем пересечение столбца, соответствующего величине 0,025, и строки, соответствующей 99 степеням свободы. В этой ячейке записано критическое значение, равное 1,9842. Поскольку t-распределение является симметричным и его математическое ожидание равно 0, площади, ограниченной правым хвостом, соответствует величина +1,9842, а площади, ограниченной левым хвостом, соответствует величина –1,9842. Величина 1,9842 означает следующее: вероятность того, что величина t превосходит +1,9842, равна 0,025, т.е. 2,5% (рис. 7).
Рис. 7. Распределение Стьюдента с 99 степенями свободы
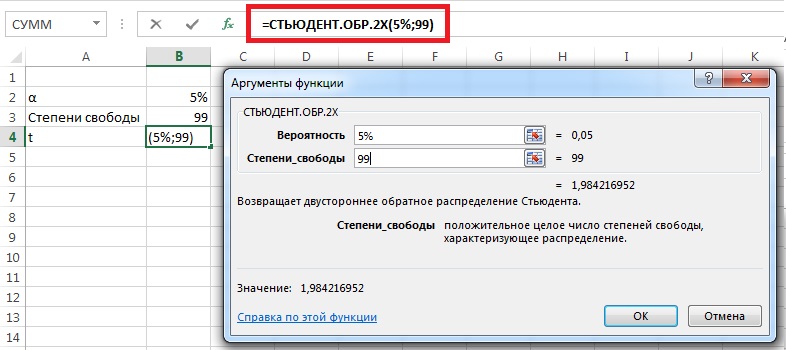
Вместо таблиц удобнее и проще использовать функции Excel (к сожалению, эти функции вуалируют суть расчетов, так что иметь представление о механике расчета всё же полезно). Начиная с версии 2010 вместо таблиц используется функция =СТЬЮДЕНТ.ОБР.2Х() (рис. 8)
Рис. 8. Использование функции =СТЬЮДЕНТ.ОБР.2Х() для определения t-параметра по известной вероятности (обратная задача построению плотности распределения)
Степени свободы. Для вычисления выборочной дисперсии S2 необходимо вычислить величину
Таким образом, для вычисления выборочной дисперсии необходимо знать ![]() . Следовательно, мы можем варьировать лишь n – 1 выборочное значение. Это означает, что величина обладает n – 1 степенями свободы. Допустим, например, что выборка состоит из 5 чисел, а ее выборочное среднее равно 20. Сколько разных значений необходимо знать для того, чтобы однозначно определить остальные? Если n = 5 и
. Следовательно, мы можем варьировать лишь n – 1 выборочное значение. Это означает, что величина обладает n – 1 степенями свободы. Допустим, например, что выборка состоит из 5 чисел, а ее выборочное среднее равно 20. Сколько разных значений необходимо знать для того, чтобы однозначно определить остальные? Если n = 5 и ![]() = 20, то
= 20, то
поскольку
Таким образом, если известны четыре величины, пятое значение уже не свободно, поскольку сумма должна быть равна 100. Например, если нам известны величины 18, 24, 19 и 16, пятая величина должна быть равной 23, поскольку сумма равна 100.
Доверительный интервал. Рассмотрим формулу для вычисления интервала, содержащего математическое ожидание при неизвестном стандартном отклонении с вероятностью (1 – α)х100%.
где tn – 1 — критическое значение t-распределения с n – 1 степенями свободы, соответствующее площади, ограниченной правым хвостом и равной α/2.
Проиллюстрируем применение этой формулы. Предположим, что при аудиторской проверки из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что выборочное среднее равно 110,27долл., а выборочное стандартное отклонение — 28,95 долл. Если компания желает построить интервал, имеющий доверительный уровень, равный 95%, критическое значение t-распределения равно 1,9842 (см. табл. 7.1). Используя формулу доверительного интервала получаем:
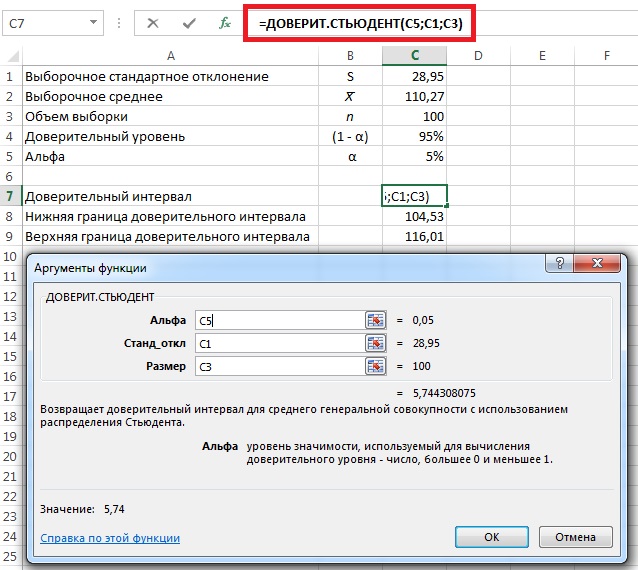
Кроме уже перечисленных в Excel есть еще целый ряд функций, работающих с t-распределением Стьюдента. Например, вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью Excel продемонстрировано на рис. 9. Заметим, что до версии 2010 Excel не содержит функции, непосредственно рассчитывающей доверительный интервал для t-распределения Стьюдента.
Рис. 9. Вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью функции Excel =ДОВЕРИТ.СТЬЮДЕНТ()
Таким образом, вероятность того, что средняя сумма накладных находится в интервале от 104,53 до 116,01, равна 95%.
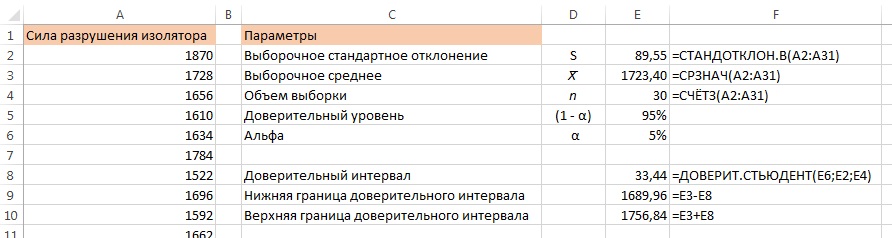
Рассмотрим пример 2. Некая промышленная компания на Среднем Западе производит электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания, в ходе которых определяется максимальная сила, необходимая для разрушения изолятора. Сила измеряется в фунтах нагрузки, приводящей к разрушению изолятора (рис. 10, столбец А). Постройте интервал, содержащий математическое ожидание генеральной совокупности величин силы, необходимой для разрушения изолятора, доверительный уровень которого равен 95%.
Решение. Как показано на рис. 10, выборочное среднее равно ![]() =1723,4 фунта, а выборочное стандартное отклонение равно S = 89,55 фунта.
=1723,4 фунта, а выборочное стандартное отклонение равно S = 89,55 фунта.
Рис. 10. Результаты экспериментов и расчет доверительного интервала
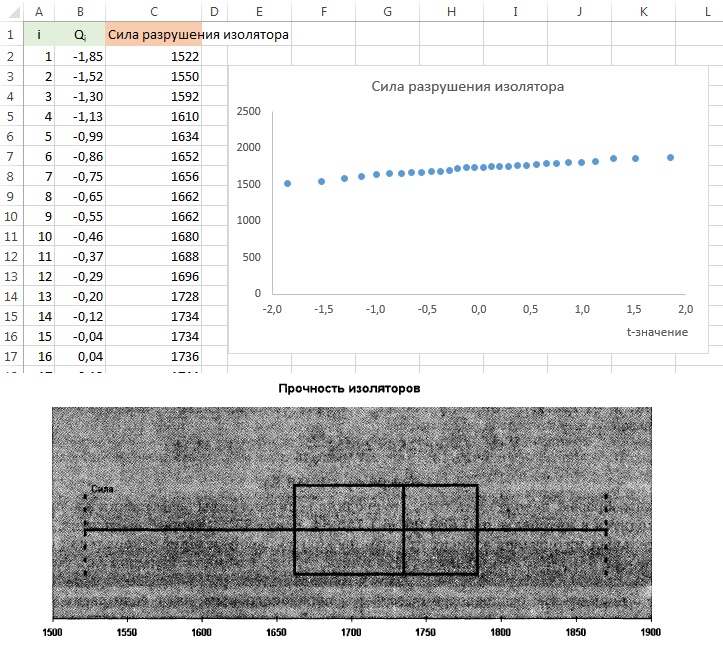
Вероятность того, что средняя величина силы разрушения изолятора находится в интервале от 1689,96 до 1756,84, равна 95%. Корректность этих доверительных интервалов зависит от того, насколько распределение генеральной совокупности близко к нормальному. Напомним, что требование о большом объеме выборки можно ослабить. Таким образом, если объем выборки равен 30, предположение о нормальном распределении остается правдоподобным, даже если распределение силы разрушения слегка асимметрично. График нормального распределения (рис. 11а) и блочная диаграмма (рис. 11б) свидетельствуют о том, что распределение силы разрушения имеет легкую асимметрию, следовательно, для решения задачи можно применять t-распределение.
Рис 11. Средняя величины силы, необходимой для разрушения изолятора: (а) график нормального распределения (подробнее о том, как построить такой график см. Проверка гипотезы о нормальном распределении); (б) блочная диаграмма (подробнее о построении таких диаграмм см. Excel. Биржевая диаграмма, она же блочная, она же ящичная)
Построение доверительного интервала для доли признака в генеральной совокупности
В этом разделе понятие доверительного интервала распространяется на категорийные данные. Это позволяет оценить долю признака в генеральной совокупности р с помощью выборочной доли рS = Х/n. Как указывалось ранее, если величины nр и n(1 – р) превышают число 5, биномиальное распределение можно аппроксимировать нормальным. Следовательно, для оценки доли признака в генеральной совокупности р можно построить интервал, доверительный уровень которого равен (1 – α)х100%.
где pS — выборочная доля признака, равная Х/n, т.е. количеству успехов, деленному на объем выборки, р — доля признака в генеральной совокупности, Z — критическое значение стандартизованного нормального распределения, n — объем выборки.
Пример 3. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что 10 из этих накладных составлены с ошибками. Таким образом, р = 10/100 = 0,1. Доверительному уровню 95% соответствует критическое значение Z = 1,96.
Таким образом, вероятность того, что от 4,12% до 15,88% накладных содержат ошибки, равна 95%.
Для заданного объема выборки доверительный интервал, содержащий долю признака в генеральной совокупности, кажется более широким, чем для непрерывной случайной величины. Это объясняется тем, что измерения непрерывной случайной величины содержат больше информации, чем измерения категорийных данных. Иначе говоря, категорийные данные, принимающие лишь два значения, содержат недостаточно информации для оценки параметров их распределения.
Вычисление оценок, извлеченных из конечной генеральной совокупности
Оценка математического ожидания. Поправочный коэффициент для конечной генеральной совокупности (fpc) ранее использовался для уменьшения стандартной ошибки в ![]() раз. При вычислении доверительных интервалов для оценок параметров генеральной совокупности поправочный коэффициент применяется в ситуациях, когда выборки извлекаются без возвращения. Таким образом, доверительный интервал для математического ожидания, имеющий доверительный уровень, равный (1 – α)х100%, вычисляется по формуле:
раз. При вычислении доверительных интервалов для оценок параметров генеральной совокупности поправочный коэффициент применяется в ситуациях, когда выборки извлекаются без возвращения. Таким образом, доверительный интервал для математического ожидания, имеющий доверительный уровень, равный (1 – α)х100%, вычисляется по формуле:
Пример 4. Чтобы проиллюстрировать применение поправочного коэффициента для конечной генеральной совокупности, вернемся к задаче о вычислении доверительного интервала для средней суммы накладных, рассмотренной выше в примере 3. Предположим, что за месяц в компании выписываются 5000 накладных, причем X̅ =110,27долл., S = 28,95 долл., N = 5000, n = 100, α = 0,05, t99 = 1,9842. По формуле (6) получаем:
Оценка доли признака. При выборе без возвращения доверительный интервал для доли признака, имеющий доверительный уровень, равный (1 – α)х100%, вычисляется по формуле:
Доверительные интервалы и этические проблемы
При выборочном исследовании генеральной совокупности и формулировании статистических выводов часто возникают этические проблемы. Основная из них — как согласуются доверительные интервалы и точечные оценки выборочных статистик. Публикация точечных оценок без указания соответствующих доверительных интервалов (как правило, имеющих 95%-ный доверительный уровень) и объема выборки, на основе которых они получены, может породить недоразумения. Это может создать у пользователя впечатление, что точечная оценка — именно то, что ему необходимо, чтобы предсказать свойства всей генеральной совокупности. Таким образом, необходимо понимать, что в любых исследованиях во главу угла должны быть поставлены не точечные, а интервальные оценки. Кроме того, особое внимание следует уделять правильному выбору объемов выборки.
Чаще всего объектами статистических манипуляций становятся результаты социологических опросов населения по тем или иным политическим проблемам. При этом результаты опроса выносят на первые страницы газет, а ошибку выборочного исследования и методологию статистического анализа печатают где-нибудь в середине. Чтобы доказать обоснованность полученных точечных оценок, необходимо указывать объем выборки, на основе которой они получены, границы доверительного интервала и его уровень значимости.
Предыдущая заметка Выборочные распределения
Следующая заметка
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 448–462
[2] Центральная предельная теорема утверждает, что при достаточно большом объеме выборок выборочное распределение средних можно аппроксимировать нормальным распределением. Это свойство не зависит от вида распределения генеральной совокупности.
[3] На мой взгляд авторы некорректно используют такую точность; если измерения ведутся с точностью до тысячной дюйма, то и вычисления следует округлять до той же точности. Я бы записал ![]() = 10,998 ± 0,004; 10,994 < μ < 11,002
= 10,998 ± 0,004; 10,994 < μ < 11,002