8. Статистика

Я преподаю магистрам курс «Статистическое мышление» и, объясняя термин пространство исходов, в качестве примера рассказываю о парадоксе Монти Холла. Напомню условия задачи в её классическом виде. Вы участник шоу, и вам показывают три одинаковые двери. За одной – авто, за двумя другими – козы. Монти Холл, ведущий шоу, просит вас выбрать одну из дверей. Вы делаете это, но не открываете выбранную дверь. Монти, который знает, где находится авто, открывает одну из двух других дверей. Он выбирает свою дверь в соответствии со следующими правилами:

• Монти всегда открывает дверь, за которой скрывается коза.
• Монти никогда не открывает дверь, которую вы выбрали изначально.
• Если Монти может открыть более одной двери, не нарушив первые два правила, то он выбирает свою дверь случайным образом.

После того, как Монти откроет свою дверь, он предлагает вам остаться с первоначальным выбором или переключиться на другую неоткрытую дверь. Что нужно сделать, чтобы максимизировать свои шансы на выигрыш автомобиля? Обоснуйте свой ответ прежде чем читать далее.

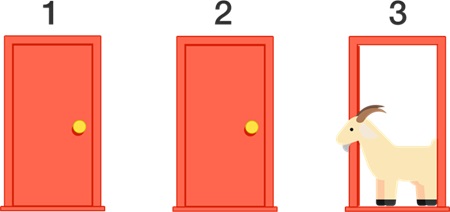
Рис. 1. Классические правила: после вашего выбора Монти Холл открывает одну из двух оставшихся дверей, за которой скрывается коза

Подробнее »Объяснение парадокса Монти Холла

Недавно прочитал книгу Вэй Цзи Ма. Байесовские модели восприятия и действия, и мне понравилось введение в теорию вероятностей, вынесенное в приложение. Кратко и оригинально.

Алгебра помогает понять математику, а теория вероятностей помогает понять жизнь. К сожалению, теория вероятностей не является стандартным компонентом большинства учебных программ бакалавриата. Мы надеемся, что это изменится, а пока предлагаем ознакомиться с некоторыми основами теории вероятностей. Это ни в коем случае не исчерпывающее введение, которое можно найти в учебнике по теории вероятностей. Это краткий справочник, который сосредоточен только на концепциях и расчетах, используемых в книге.

Подробнее »Основы теории вероятностей

Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. В этой серии ранее опубликовал Среднеквадратичное отклонение и среднее абсолютное отклонение, Моделирование сходимости центральной предельной теоремы. В настоящей заметке рассматривается мета-распределение p-значений, относящееся к распределениям с жирными хвостами.

Рис. 1. Распределение вероятностей однохвостого p-значения при математическом ожидании 0,11, сгенерированное как методом Монте-Карло (гистограмма), так и аналитически (график непрерывной линией). Грубая асимметрия распределения делает среднее значение существенно выше большинства наблюдений, создавая многочисленные иллюзии статистической значимости.

Подробнее »Мета-распределение p-значений

Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. В этой серии уже опубликовал Среднеквадратичное отклонение и среднее абсолютное отклонение. Настоящая заметка посвящена экспериментам со сходимостью центральной предельной теоремы (ЦПТ).

Рис. 1. Самая быстрая ЦПТ: равномерное распределение сходится к гауссову за несколько шагов

Подробнее »Моделирование сходимости центральной предельной теоремы

Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. Заметка представляет собой смесь текста Талеба, моих моделей в Excel и кратких замечаний.

Начнем со среднеквадратического отклонения и дисперсии, как свойств высших моментов (точнее, вторых). Есть различие между среднеквадратическим отклонением и средним абсолютным отклонением, и это различие усиливается в случае жирных хвостов.

Рис. 1. Сравним поведение взвешивающих функций корень(K + x²) и K +|x|. При жирном хвосте среднеквадратическое отклонение расходится со средним абсолютным отклонением при больших значениях случайной величины х

Подробнее »Среднеквадратичное отклонение и среднее абсолютное отклонение

Недавно прочитал книгу Майкла Херцога с соавторами Статистика и планирование эксперимента для непосвященных. В ней я в очередной раз встретился со статистической мощностью. До сих пор я относился к этой статистике несколько академически. Что называется, не чувствовал её на кончиках пальцев. Некоторые разделы книги Херцога меня заинтересовали, я построил пару моделей в Excel и осознал, что статистическая мощность – это вероятность получить в эксперименте статистически значимые результаты. Кроме того, я нашел формулу расчета статистической мощности в Excel. Свои выводы я представил в заметке Статистическая мощность эксперимента в Excel. В книге Майкл Херцог также упоминает о калькуляторе статистической мощности G*Power. Предлагаю вам краткий обзор программы G*Power основанный на переводе статьи Susanne Mayr, Edgar Erdfelder, Axel Buchner, Franz Faul. A short tutorial of GPower, опубликованной в журнале Tutorials in Quantitative Methods for Psychology. – 2007, Vol. 3(2), p. 51–59.

Рис. 1. Анализ статистической мощности в GPower: апостериорный t-тест для независимых выборок

Подробнее »Онлайн калькулятор статистической мощности G*Power

Недавно прочитал книгу Майкла Херцога с соавторами Статистика и планирование эксперимента для непосвященных. В ней я в очередной раз встретился со статистической мощностью. До сих пор я относился к этой статистике несколько академически. Что называется, не чувствовал её на кончиках пальцев. Некоторые разделы книги Херцога меня заинтересовали, я построил пару моделей в Excel, и до меня дошла суть статистической мощности. Я понял, что статистическая мощность – вероятность получить в эксперименте статистически значимые результаты. Кроме того, я нашел формулу расчета статистической мощности в Excel.

Рис. 1. Нормально распределенные случайные величины. Выборка 1 – N(0;1), Выборка 2 – N(1;1)

Подробнее »Статистическая мощность эксперимента в Excel

Эта заметка родилась на стыке трех моих увлечений: футбол, Excel и статистика)) Известно, что число голов, забитых каждой командой в одном матче подчиняется распределению Пуассона. Я решил проверить это на результатах матчей английской премьер-лиги сезона 2021/2022. Всего было 38 туров по 10 матчей в туре, по две команды в одном матче. Итого 760 исходных значений.

Рис. 1. Распределение числа забитых голов

Скачать заметку в формате Word или pdf, примеры в формате ExcelПодробнее »Статистический вывод на основе критерия Колмогорова

Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения – чем стандартное отклонение отличается от стандартной ошибки, и в каких случаях, применять ту или иную статистику. А недавно в книге Искусство статистики Дэвида Шпигельхалтера я узнал про бутстрэппинг, и понял, как объяснить различия стандартного отклонения и стандартной ошибки.

Для начала зададим 100 значений стандартной нормально распределенной случайной величины. В этом контексте стандартная означает, что ее матожидание μ = 0, а среднеквадратичное отклонение σ = 1. Поскольку значения в Excel получены с помощью волатильной функции СЛМАССИВ(), после любого действия они пересчитываются. Поэтому диаграммы в заметке и в файле будут отличаться.

Рис. 1. Нормально распределенная случайная величина

Подробнее »Стандартное отклонение и стандартная ошибка

Недавно прочитал Искусство статистики Дэвида Шпигельхалтера. На тему байесовской вероятности очень понравился пример с монетами. Сначала – фрагмент книги, а затем небольшая модель в Excel.

У вас в кармане три монеты: на одной два орла, на другой две решки, третья обычная. Вы наугад вытаскиваете монету, подбрасываете ее, и выпадает орел. Какова вероятность, что на другой стороне монеты тоже орел? Дайте свой ответ, прежде чем читать далее.

Рис. 1. Три монеты

Подробнее »Нетривиальный Байес