В предыдущей заметке χ2-критерий применялся для оценки разностей между несколькими долями признака. Если таблица сопряженности признаков состоит из r строк и с столбцов, χ2-критерий можно использовать для проверки независимости двух категорийных величин. [1] В этом случае нулевая и альтернативная гипотезы формулируются следующим образом: Н0: две категорийные величины независимы (т.е. между ними нет взаимосвязи), Н1: две категорийные величины зависят друг от друга (т.е. между ними есть взаимосвязь).
Для иллюстрации применяемых методов используется сценарий, в котором оценивается степень удовлетворенности постояльцев отелей, принадлежащих компании Т. С. Resort Properties. Если гости удовлетворены обслуживанием, велика вероятность, что они вернутся на следующий год и порекомендуют своим друзьям остановиться именно в вашем отеле. Чтобы оценить качество обслуживания, постояльцев просят заполнить анкету и указать, довольны ли они гостеприимством.
Для проверки независимости, как и прежде, применяется тестовая χ2-статистика:
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
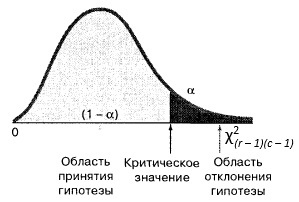
При заданном уровне значимости α нулевая гипотеза отклоняется, если вычисленная χ2-статистика больше верхнего критического значения χU2, присущего χ2-распределению с (r – 1)(с – 1) степенями свободы. Решающее правило выглядит следующим образом: гипотеза Н0 отклоняется, если χ2 > χU2 (рис. 1); в противном случае гипотеза Н0 не отклоняется.
Рис. 1. Критическая область χ2-критерия для проверки независимости двух переменных в факторной таблице r*c
Альтернативой χ2-критерию для проверки гипотезы о равенстве долей служит χ2-критерий независимости. В обоих случаях применяется одна и та же тестовая статистика и одно и то же решающее правило, правда, выводы делаются разные. Так, в задаче о постояльцах двух гостиниц, рассмотренной ранее, между процентными долями гостей, планирующих вернуться в гостиницу в следующем сезоне, обнаружилась значимая разница. С другой стороны, можно сделать вывод, что между отелями и вероятностью, что гости в них вернутся, есть тесная зависимость. Несмотря на это, между двумя этими критериями существуют принципиальные различия. Основное различие заключается в схеме формирования выборок.
При проверке гипотезы о равенстве долей рассматривается один фактор, имеющий несколько уровней. Разным уровням соответствуют разные выборки, извлеченные из независимых генеральных совокупностей. Категориальные ответы в каждой из выборок классифицируются по двум категориям — успех и неудача. Цель критерия — сравнить и оценить разности между долями успеха для разных уровней фактора. В то же время при проверке независимости рассматриваются два фактора, каждый из которых имеет несколько уровней. Из генеральной совокупности извлекается одна выборка, а в ячейки таблицы сопряженности признаков помещаются значения двух категорийных переменных, соответствующие разным уровням факторов.
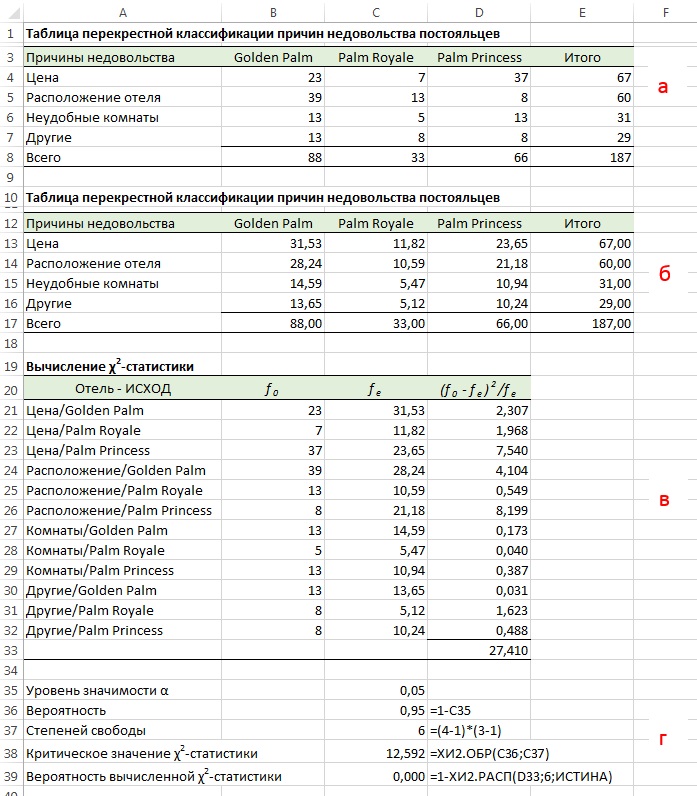
Для того чтобы проиллюстрировать χ2-критерий независимости, предположим, что в ходе опроса постояльцев трех отелей, принадлежащих компании Т. С. Resort Resources, гостей, решивших не возвращаться, просили указать причину. Их ответы приведены на рис. 2а.
Рис. 2. Таблица перекрестной классификации причин недовольства постояльцев: (а) наблюдаемое количество f0; (б) ожидаемое количество f1; (в) χ2-статистика; (г) расчет критического значения χU2
Результаты анкетирования говорят о том, что 67 постояльцев недовольны ценой, 60— расположением отеля, 31 — комнатами и 29 имеют другие причины для недовольства. В таблице сопряженности признаков учтены ответы 88 постояльцев отеля Golden Palm, 33 гостей отеля Palm Royale и 66 отдыхающих из отеля Palm Princess, не планирующих возвращаться на следующий год. Величины, заполнившие ячейки факторной таблицы 4×3, представляют собой количество ответов гостей, недовольных обслуживанием в зависимости от конкретных причин. Нулевая и альтернативная гипотезы таковы: Н0: между недовольством постояльцев и конкретным фактором нет взаимосвязи, Н1: между недовольством постояльцев и конкретным фактором есть взаимосвязь. Для проверки нулевой гипотезы применяется тестовая χ2-статистика:
где f0 — наблюдаемое количество успехов или неудач в конкретной ячейке факторной таблицы r*c, fе — теоретическое, или ожидаемое, количество успехов или неудач в конкретной ячейке таблицы сопряженности признаков при условии, что нулевая гипотеза является истинной.
Для вычисления величины fе используется правило умножения вероятностей независимых событий. Например, если нулевая гипотеза о независимости верна, вероятность, или ожидаемая доля успехов, соответствующих левой верхней ячейке, вычисляется путем умножения двух вероятностей:
Р(цена и отель Golden Palm) = Р(цена) х Р(отель Golden Palm).
Здесь доля постояльцев, указавших в качестве причины своего недовольства слишком высокую цену, равна 67/187, или 0,3583, а доля всех ответов, поступивших от постояльцев отеля Golden Palm, равна 88/187, или 0,4706. Если нулевая гипотеза верна, и основная причина недовольства гостей и характеристика отеля не связаны между собой, ожидаемая доля, или вероятность Р(цена и отель Golden Palm), окажется равной произведению отдельных вероятностей Р(цена) и Р(отель Golden Palm), т.е. 0,3583 х 0,4706 = 0,1686. Тогда ожидаемая величина fе для каждой ячейки должна быть произведением суммарного объема выборок n на эту вероятность: 187 х 0,1686, т.е. 31,53. Величины fе для оставшихся ячеек факторной таблицы 4×3 вычисляются аналогично (рис. 2б). Более простой способ вычисления ожидаемых величин, не требующих сложных вычислений, основан на формуле:
(2) fe = (общая сумма по строке * общая сумма по столбцу) / n
где n — суммарный объем выборок.
Тестовая статистика (1) аппроксимируется χ2-распределением, количество степеней свободы которого равно (r – 1)(с – 1) (рис. 2в). Вычисленная χ2-статистика равна 27,402.
Установим уровень значимости α = 0,05. Поскольку χ2-распределение для факторной таблицы 4*3 имеет 6 степеней свободы, критическое значение χ2-статистики можно определить с помощью функции Excel =ХИ2.ОБР(0,95;6) = 12,592 (рис. 2г). Вычисленная χ2-статистика превышает критическое значение (27,402 > 12,592), следовательно, нулевая гипотеза отклоняется (рис. 3). С другой стороны, p-значение равно 0,000 < 0,05. Следовательно, и по этому критерию нулевая гипотеза о независимости между причиной недовольства и конкретными характеристиками отеля отклоняется. Кроме того, р-значение свидетельствует о том, что обнаружить разность между выборочными долями постояльцев, не удовлетворенных обслуживанием в трех отелях и указавших разные причины, практически невозможно, если причины недовольства постояльцев никак не связаны с характеристиками отеля. Следовательно, между причинами недовольства и характеристиками отелей существует тесная взаимосвязь.
Рис. 3. Проверка гипотезы о независимости переменных в опросе недовольных постояльцев отелей при уровне значимости α = 0,05 и шести степенях свободы
Сравнение наблюдаемых и ожидаемых величин (рис. 2в) показывает, что цена не играет особой роли для постояльцев отеля Golden Palm, а для гостей отеля Palm Princess она кажется слишком высокой. В то же время расположение отеля Golden Palm многие постояльцы сочли неудачным, хотя гости отеля Palm Princess не считают это важным фактором.
Проверка предположений, касающихся факторной таблицы r*с. Для получения точных результатов на основе данных, приведенных в факторной таблице r*с, необходимо, чтобы количество успехов или неудач было достаточно большим. На нее распространяются правила, сформулированные для факторной таблицы 2*с. Иначе говоря, ни одна ячейка не должна содержать нулей. Чтобы удовлетворить это условие, категории, содержащие нули, следует объединить в одну. Эта процедура позволяет увеличить количество успехов или неудач в ячейках таблицы сопряженности признаков и повысить точность критерия.
Предыдущая заметка Применение χ2-критерия для проверки гипотезы о равенстве двух или нескольких долей
Следующая заметка Непараметрические критерии. Ранговый критерий Уилкоксона
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 730–738