Дэвид Шпигельхалтер. Искусство статистики. Как находить ответы в данных

Статистика играла ключевую роль в научном познании мира на протяжении веков, а в эпоху больших данных базовое понимание этой дисциплины и статистическая грамотность становятся критически важными. Дэвид Шпигельхалтер приглашает вас в не обремененное техническими деталями увлекательное знакомство с теорией и практикой статистики.

Эта книга предназначена как для студентов, которые хотят ознакомиться со статистикой, не углубляясь в технические детали, так и для широкого круга читателей, интересующихся статистикой, с которой они сталкиваются на работе и в повседневной жизни. Но даже опытные аналитики найдут в книге интересные примеры и новые знания для своей практики.

Дэвид Шпигельхалтер. Искусство статистики. Как находить ответы в данных. – М.: Манн, Иванов и Фербер, 2021. – 448 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 6% от объема книги)

Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon или Лабиринте

Код на языке R и данные для воспроизведения большей части анализов и рисунков можно найти на сайте.

Введение

Наука о данных и грамотность в работе с ними требуют подхода, направленного на решение основных проблем, где применение конкретных статистических инструментов рассматривается лишь как один из компонентов цикла исследований. Цикл PPDAC (Problem, Plan, Data, Analysis, Conclusion) был предложен как модель решения проблем. Рисунок 1 основан на примере Новой Зеландии, которая считается мировым лидером по преподаванию статистики в школах.

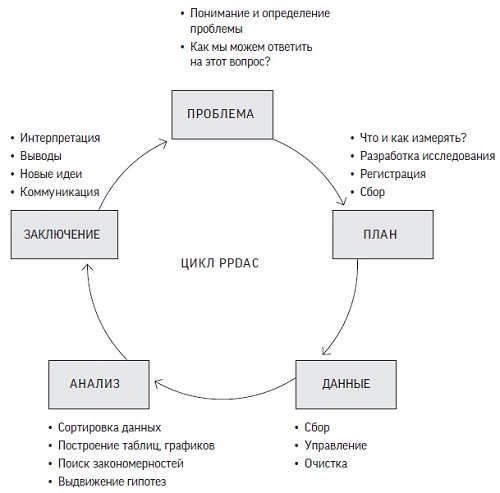
Рис. 1. Цикл решения проблем PPDAC

Глава 1. Расчет долей: качественные данные и проценты

Бинарные переменные могут принимать только два значения (да/нет). Качественная (или категорийная) переменная — это переменная, которая может принимать одно, два или более значений, попадающих в ту или иную категорию. Категории могут быть:

неупорядоченными: страна рождения, цвет автомобиля или больница, где делали операцию;
упорядоченными: воинские звания;
сгруппированными числами: степени ожирения, которые часто определяются в терминах пороговых значений по индексу массы тела (ИМТ) .

Сравнение двух долей. В ноябре 2015 года Международное агентство по изучению рака (МАИР) сообщало, что ежедневное употребление 50 граммов обработанного мяса связано с повышением риска развития рака кишечника на 18%. Звучит тревожно? Статистики представили этот относительный показатель в абсолютных значениях. При нормальном ходе вещей примерно 6 из каждых 100 человек, которые не едят бекон ежедневно, заболеют раком кишечника. Если же 100 таких человек ели бы бекон ежедневно всю жизнь, то можно было бы ожидать, что больных будет на 18% больше, то есть не 6, а 7 человек из 100.

Риски полезно выражать в ожидаемых частотах, то есть вместо того, чтобы обсуждать доли или вероятности, просто спросить: «А что это означает для группы в 100 (или 1000) человек?». Психологические исследования продемонстрировали, что такой метод улучшает понимание. Утверждение, что потребление мяса приводит к «18%-ному повышению риска», можно считать манипулятивным, поскольку такая форма подачи информации создает преувеличенное впечатление о степени опасности. Вот как честно отразить эти данные:

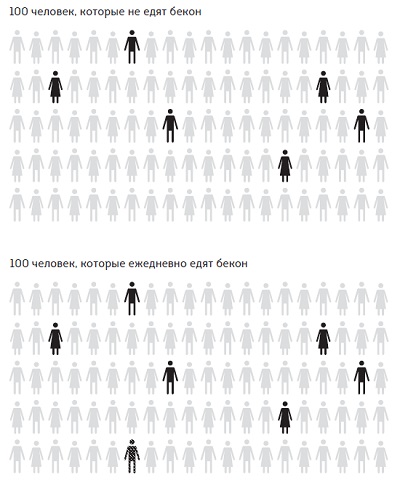
Рис. 2. «Раковые» пиктограммы

Глава 2. Числовые характеристики выборки и представление данных

Альберто Каиро определил четыре признака хорошей визуализации данных.

Содержит достоверную информацию.
Схема выбрана так, чтобы были заметны закономерности.
Выглядит привлекательно, при этом внешний вид не мешает правдивости, ясности и глубине.
Когда это уместно, способ организации позволяет проводить исследования. Например, позволить аудитории взаимодействовать с визуализацией.

Когда мы хотим донести до аудитории важное сообщение, содержащееся в данных, мы можем применить инфографику или визуализацию, чтобы привлечь внимание людей и рассказать хорошую историю.

Еще более продвинутой является динамическая графика, где движение используется для выявления закономерностей изменений с течением времени. Специалистом по такой методике был Ханс Рослинг, чьи выступления на конференция TED и видеоролики установили новый стандарт для выступлений с применением статистики, например демонстрация взаимосвязи между изменениями благосостояния и здоровья с помощью перемещения пузырьков, отражающих прогресс в каждой стране с 1800 года до наших дней. Рослинг использовал графику, чтобы исправить ошибочное представление о различии между развитыми и слаборазвитыми странами: динамические графики показывали, что со временем почти все страны стабильно двигались по одному и тому же пути в сторону улучшения благосостояния и процветания.

Глава 3. Почему мы смотрим на данные? Совокупности и измерение

Выводы из данных — процесс «индуктивного умозаключения». Многие люди имеют некоторое смутное представление о дедукции благодаря Шерлоку Холмсу, использовавшему ее при поиске преступников (на самом деле Шерлок Холмс использовал абдукцию). В реальной жизни дедукция — это процесс применения правил логики для перехода от общего к частному. Если согласно законодательству в стране установлено правостороннее движение, то мы можем прийти к дедуктивному заключению, что в любой ситуации лучше ехать по правой стороне. Индукция работает наоборот: на основании частных случаев предпринимаются попытки сделать общие заключения. Принципиальное отличие индукции от дедукции состоит в том, что дедукция дает истинные заключения, а индукция — в общем случае нет.

Индуктивное умозаключение можно представить в виде шагов, связанных с переходом от данных к конечной цели исследования.

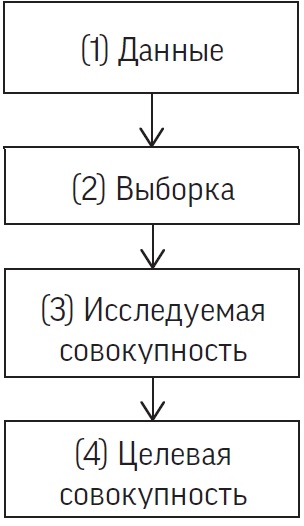
Рис. 3. Процесс индуктивного умозаключения

Существуют три вида генеральных совокупностей, из которых мы можем делать выборки:

Буквальная совокупность. Например, выбор случайным образом человека при опросе.
Виртуальная совокупность. Измерение кровяного давления. Мы можем сделать несколько измерений и получить немного другие результаты. Думайте об этом как о получении наблюдений из виртуальной совокупности всех измерений, которые могли бы сделать, если бы имели достаточно времени.
Метафорическая совокупность. В этом случае никакой большей совокупности нет вообще. Подумайте о количестве ежегодно совершаемых убийств, результатах экзаменов для определенного класса или данных обо всех странах мира — ни в одном из этих случаев мы не можем считать имеющиеся данные выборкой из какой-то фактической совокупности.

О метафорической совокупности предпочтительнее думать, что наши наблюдения берутся из некоего воображаемого пространства возможностей. Например, мировая история такая, какая есть, но мы можем представить, что она развивалась по совершенно иному сценарию, а мы просто оказались в одном из ее возможных состояний. Это множество альтернативных историй можно считать метафорической совокупностью. Когда мы рассматривали детские операции в Соединенном Королевстве за 2012–2015 годы, у нас были полные данные о детях за этот период: мы знали и число смертей, и число выживших. Однако мы можем себе представить истории, в которых выжили бы другие дети вследствие непредвиденных обстоятельств, которые мы склонны именовать «случайностью».

Глава 4. Причины и следствия

Похоже, у людей есть глубокая внутренняя потребность объяснять происходящее в виде простейшей зависимости причина –> следствие. Существует даже специальное слово для склонности конструировать связи между событиями, которые в реальности не связаны, — апофения, причем ее крайнее проявление — объяснять простую случайность или невезение злонамеренностью других и даже колдовством. К сожалению (а, возможно, к счастью), мир несколько сложнее, чем колдовство. И первая сложность появляется при попытке понять, что подразумевается под причиной.

Статистическая идея причинности не строго детерминистская. Когда мы говорим, что X обусловливает Y, мы не имеем в виду, что каждый раз, когда наступает X, наступает и Y. Мы всего лишь подразумеваем: если X происходит чаще, то и Y случается чаще. Мы не можем сказать, что X вызывает Y, а можем лишь утверждать, что X увеличивает долю случаев, когда происходит Y.

Новое в рандомизированных экспериментах — A/B-тестирование в веб-дизайне, при котором пользователей направляют на различные варианты веб-страницы (о чем они не знают). Далее измеряется количество времени, проведенного на том или ином варианте страницы, переходов по рекламным объявлениям и так далее.

Глава 5. Моделирование зависимости с помощью регрессии

В регрессионном анализе зависимой переменной называется величина, которую мы хотим предсказать или объяснить (по оси Y). Независимая переменная – это величина, которую мы используем для прогноза или объяснения (по оси Х). Наклон регрессионной прямой называется коэффициентом регрессии.

Линия регрессии – пример статистической модели. У статистических моделей есть два основных компонента:

математическая формула, которая выражает детерминистский, предсказуемый компонент,
остаточная ошибка – рассеяние реальных данных вокруг регрессионной прямой.

Это классическая идея сигнала и шума.

У нас сильная психологическая склонность приписывать перемены какому-нибудь вмешательству, и это делает сравнения «до и после» ненадежными. Полосы удач и неудач не бесконечны, и в конце концов все возвращается на круги своя — это тоже можно воспринимать как регресс к среднему. Но когда мы убеждены, что полосы везения-невезения отражают постоянное состояние дел, мы ошибочно будем рассматривать возврат к нормальному состоянию как следствие какого-либо нашего вмешательства.

Исследователи используют четыре основные стратегии моделирования:

Простые модели линейной регрессии.
Сложные детерминистские модели, основанные на научном понимании физических процессов, например, используемые при прогнозировании погоды.
Сложные алгоритмы, используемые для принятия решений и прогнозов, основанных на анализе большого количества прошлых случаев — например, для рекомендации книг, которые вы, возможно, хотели бы купить в сетевом магазине. Они часто будут «черными ящиками» в том смысле, что могут делать хорошие прогнозы, но их внутренняя структура в какой-то степени непостижима.
Регрессионные модели, которые делают заключения о причинно-следственных связях; за них выступают экономисты.

Британский статистик Джордж Бокс прославился бесценным афоризмом: «Все модели неверны, но некоторые полезны». Финансовый кризис 2007–2008 годов в значительной степени был вызван чрезмерным доверием к сложным финансовым моделям, которые использовались для определения рисков, например ипотечных пакетов.

Различные виды зависимых переменных

Не все данные являются непрерывными измерениями, такими как рост. В статистическом анализе зависимые переменные часто могут иметь другой вид: доля случаев, когда произошло какое-нибудь событие (например, доля людей, переживших операцию), количество каких-нибудь событий (например, число выявленных случаев рака в год в определенном регионе) или продолжительность времени до определенного события (например, количество лет, которое пациент прожил после операции). Для каждого из таких видов зависимых переменных существуют собственные формы множественной регрессии, и соответственно меняется интерпретация получающихся коэффициентов.

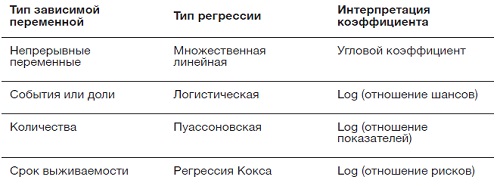
Рис. 3а. Виды множественной регрессии, используемые для различных типов зависимых переменных, а также интерпретация коэффициента для каждой независимой переменной

Глава 6. Алгоритмы, аналитика и прогнозирование

До сих пор мы говорили, как статистика может помочь нам лучше понять, как устроен мир. Или другими словами, что происходит на самом деле, а что – просто остаточная ошибка. Однако основные идеи статистической науки сохраняются, когда мы пытаемся найти сигнал в шуме. У такого алгоритма есть два класса задач:

Классификация: сообщить, с какой ситуацией мы столкнулись. Например, пристрастия и предубеждения онлайн-покупателя или является ли объект в поле зрения робота ребенком или собакой.
Прогнозирование: сообщить, что будет дальше. Например, какая погода будет на следующей неделе, какая может быть завтра цена акций, какие продукты может купить этот клиент и не выбежит ли тот ребенок перед нашим самоуправляемым автомобилем.

Такой метод называется предсказательной аналитикой.

Алгоритм разрабатывается на тренировочных данных, а затем проверяется на тестовых. Чувствительность – это доля истинно положительных наблюдений; специфичность – доля истинно отрицательных наблюдений.

Алгоритмы часто сравниваются с помощью ROC-кривых (Receiver Operating Characteristic — рабочая характеристика приемника). Если алгоритм распределяет числа случайным образом (то есть абсолютно бесполезен), то его ROC-кривая будет диагональной линией. У лучших алгоритмов ROC-кривые подходят близко к левому верхнему краю. Способ сравнения ROC-кривых — измерить площадь под ними. Для бесполезного алгоритма она равна 0,5, а для идеального — 1.

под кривой составляет 0,82. Оказывается, для этой площади есть изящная интерпретация: если мы выбираем истинно выжившего и истинно погибшего случайным образом, то с вероятностью 82% алгоритм дает истинно выжившему большую вероятность выживания, чем истинно погибшему. Области свыше 0,80 представляют весьма хорошую эффективность разделения. Площадь под ROC-кривой — это способ измерить, насколько точно алгоритм отделяет выживших от погибших, но она не отражает сами вероятности. Категория специалистов, которые лучше всего знакомы с вероятностными прогнозами, — это синоптики.

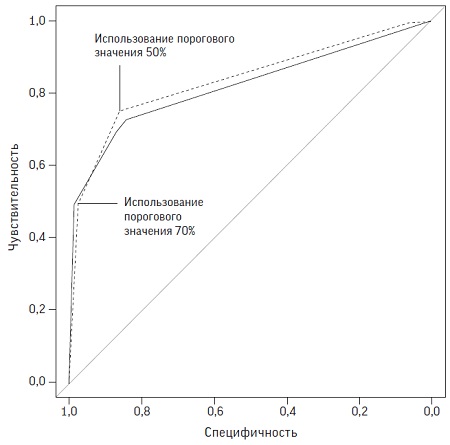
Рис. 4. Примеры ROC-кривых для тренировочного (пунктирная линия) и тестового (сплошная линия) набору данных

Если слишком хорошо подогнать алгоритм под тренировочный набор данных, его прогностическая способность может снизиться. Такое явление называется переобучением, или переподгонкой , и считается одним из самых важных вопросов при конструировании алгоритмов. Слишком усложняя алгоритм, мы фактически начинаем подгонять его под шум, а не под сигнал.

Переобучение происходит, когда мы заходим слишком далеко в стремлении приспособиться к локальным обстоятельствам, в благородном, но ложном порыве устранить смещение и учесть всю имеющуюся информацию. Переобучение приводит к уменьшению смещения, но за счет большей неопределенности или разброса в оценках, поэтому защиту от него иногда называют дилеммой смещения-дисперсии.

Необходимость в контролируемости алгоритмов, влияющих на жизнь людей, растет, и требования, чтобы выводы имели понятное объяснение, включаются в законодательство. Такие требования препятствуют использованию сложных черных ящиков и могут приводить к предпочтению (довольно старомодных) регрессионных алгоритмов, в которых влияние каждого фактора предельно ясно.

Глава 7. Насколько мы можем быть уверены в происходящем? Оценки и интервалы

В статистике важно осознавать неопределенность. Сделать оценку – часть дела, вторая часть – реалистично определить ее возможную погрешность. Предположим, мы собрали какие-то точные данные, возможно, с помощью хорошо спланированного опроса, и хотим обобщить результаты на изучаемую совокупность. Если мы проявляли осторожность и избегали внутренних смещений (скажем, обеспечив случайную выборку), то можем ожидать, что характеристики выборки будут близки к соответствующим характеристикам изучаемой совокупности.

Пусть мы опросили 760 человек. Будем выбирать их ответы по одному с возвращением в исходную выборку. Выбрав 760 раз, мы получим новую выборку. Она целиком состоит из исходных ответов, но некоторые представлены несколько раз, а некоторых нет вовсе. В результате мы получаем представление, как при перевыборках изменяется наша оценка. Процесс известен под названием бутстрэппинг — волшебная идея вытягивания себя за ремешки на обуви сопоставляется со способностью извлекать информацию из самой выборки без предположения о форме распределения всей генеральной совокупности.

Если мы повторим эту процедуру, 1000 раз, то получим 1000 возможных оценок среднего. В соответствии с центральной предельной теоремой независимо от вида распределения случайной величины, средние значения достаточно крупных выборок распределены нормально. Мы можем найти среднее средних и стандартное отклонение средних. Это и будет нашей оценкой для единственного экспериментального среднего, полученного в первоначальном опросе.

Глава 8. Вероятность — язык неопределенности и случайности

Философы и статистики выдвигают разные идеи о том, что на самом деле означают вероятности.

Классическое определение вероятности основано на симметрии монет, костей, перетасованных колод карт и так далее и может быть сформулировано как «отношение числа благоприятных исходов к числу всех исходов, если все исходы равновозможны».
«Перечислительная» вероятность. Предположим, в ящике лежат три белых и четыре черных носка. Если вытаскивать носок случайным образом, то чему равна вероятность, что он белый? Ответ 3/7 можно получить путем простого перечисления всех возможностей.
Вероятность как частота говорит о вероятности как о доле случаев, когда интересующее нас событие наступает в бесконечной последовательности идентичных экспериментов. Для бесконечно повторяющихся событий это может быть разумно, но как насчет уникальных одноразовых событий, например скачек или завтрашней погоды?
Пропенситивная интерпретация вероятности состоит в том, что у каждой ситуации есть объективная склонность порождать какое-то событие. Внешне идея выглядит привлекательно. Однако у нас, простых смертных, похоже, нет возможности оценивать такие скорее метафизические «истинные шансы».
Субъективная, или «личная», вероятность. Это степень веры конкретного человека в какое-либо событие, основанная на его нынешних знаниях. Такой подход лежит в основе байесовской школы статистики.

Если мы все наблюдаем, то откуда появляется вероятность?

Когда несколько экстремальных событий происходят в тесной последовательности (например, череда крушений самолетов или природных катастроф), появляется подозрение, что между ними существует какая-то связь. В этом случае важно выяснить, насколько необычны такие события, в чем нам и поможет следующий пример.

Чтобы оценить, насколько редок «кластер» из как минимум семи убийств в день, давайте изучим данные за три года (1095 дней) между апрелем 2014-го и мартом 2016-го. За этот период в Англии и Уэльсе было совершено 1545 убийств, то есть в среднем 1545/1095 = 1,41 в день. Ни одного дня с семью и более случаями убийства за это время не наблюдалось, однако было бы весьма наивно полагать, что такое событие невозможно. Если мы сумеем построить разумное вероятностное распределение для количества убийств в день, то сможем ответить на поставленный вопрос.

Но каковы обоснования для построения такого вероятностного распределения? Число убийств, регистрируемых в стране, — это просто факт, тут нет никакой случайной выборки и явного случайного элемента, генерирующего каждое преступление. Но какова бы ни была наша личная философия по отношению к удачам и неудачам, оказывается, полезно действовать так, словно все эти события были порождены каким-то случайным процессом, основанным на вероятности.

Давайте представим, что в начале каждого дня у нас есть огромная популяция людей, в которой у каждого ее члена есть очень малая вероятность стать жертвой убийства. Такого рода данные можно считать наблюдениями из распределения Пуассона, предложенного французским математиком Симеоном Пуассоном в 1837 году.

Тогда как нормальное (гауссовское) распределение требует двух параметров (среднее значение и среднеквадратичное отклонение), у распределения Пуассона только один параметр (он имеет смысл среднего). В нашем примере это ожидаемое ежедневное число случаев убийства = 1,41.

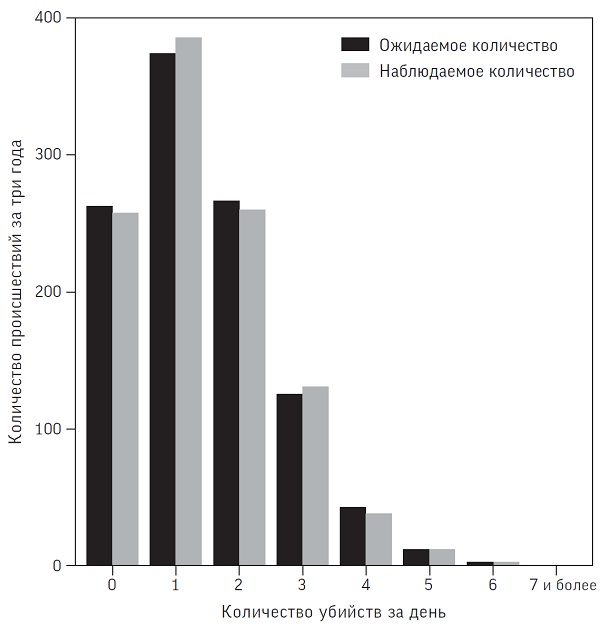
Рис. 5. Наблюдаемое и ожидаемое (по распределению Пуассона) ежедневное количество зарегистрированных убийств за 2014–2016 годы в Англии и Уэльсе

Вероятность семи и более убийств в день, исходя из распределения Пуассона равна 0,07%, а значит, такое событие можно ожидать в среднем раз в 1535 дней, то есть примерно раз в четыре года.

Предположение о «случайности» заключает в себе всю неизбежную непредсказуемость мира или то, что иногда называют естественной изменчивостью. Поэтому вероятность образует надлежащий математический фундамент как для «чистой» случайности, проистекающей из субатомных процессов, монет, костей и так далее, так и для «естественной» неизбежной изменчивости, проявляющейся в весе новорожденных, уровне выживаемости после операций, результатах экзаменов, количестве убийств и других явлениях, которые нельзя точно предсказать.

Глава 9. Объединяем вероятность и статистику

Ранее мы обсуждали идею случайной величины — одного элемента данных, извлеченного из какого-то вероятностного распределения, описываемого определенными параметрами. Но нас редко интересует только один элемент — обычно у нас большой массив данных, для которого мы вычисляем среднее, медиану и другие статистики. Фундаментальный шаг, который мы сделаем в этой главе, — рассмотрим эти статистики как случайные величины, извлеченные из их собственных распределений.

Предположим, что мы составляем выборки разного размера из совокупности, содержащей ровно 20% левшей и 80% правшей, и вычисляем вероятность получения различных возможных долей левшей. Конечно, здесь все наоборот — мы хотим по известной выборке узнать о неизвестной генеральной совокупности. Однако для этого нужно сначала исследовать, как известная совокупность порождает различные выборки.

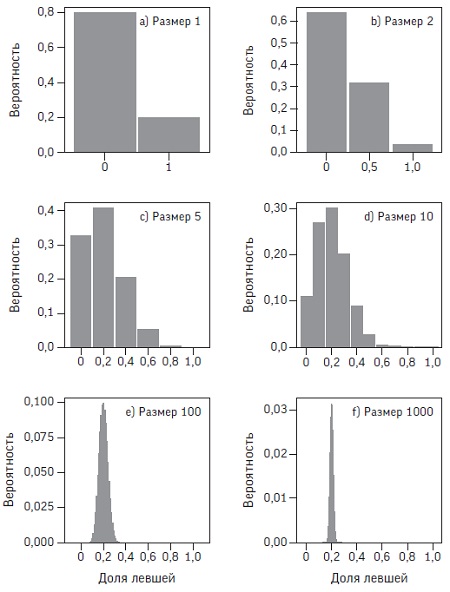
Рис. 6. Вероятностное распределение наблюдаемой доли левшей в случайных выборках по 1,2, 5, 10, 100 и 1000 человек, где истинная доля левшей в генеральной совокупности равна 0,2

Среднее значение случайной величины или математическое ожидание = 0,2, а среднеквадратичное отклонение для каждого из них зависит от размера выборки. Стандартное отклонение статистики называют стандартной ошибкой, чтобы отличить от среднеквадратичного отклонения в распределении, из которого взяты данные.

Зачастую статистические различия в малых выборках пытаются объяснить причинно-следственными связями. Так в 2011 г. на новостном сайте Би-би-си говорилось, что наблюдается трехкратное различие в уровне смертности от колоректального рака в Великобритании. Когда блогер Пол Барден наткнулся на эту статью, он провел исследование и построил диаграмму смертности населения в каждом округе:

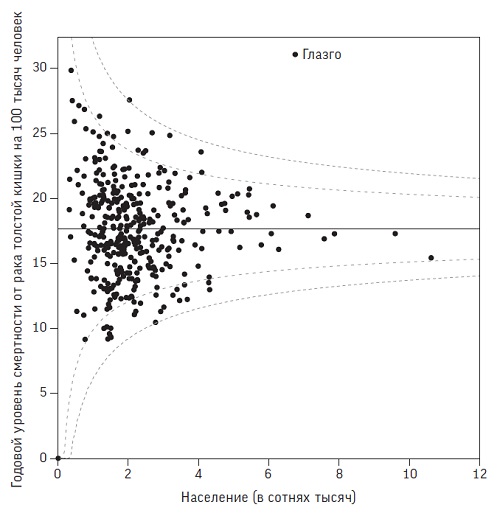
Рис. 7. Ежегодные показатели смертности от колоректального рака на 100 тысяч человек в 380 округах Великобритании в зависимости от численности населения округа

Видно, что точки (за исключением экстремального случая с Глазго-Сити) расположены в форме воронки, причем чем население округов меньше, тем разброс больше. Пол добавил граничные значения, которые показывают, куда могли бы попасть точки, если бы различия определялись естественной изменчивостью, а не какими-то систематическими отклонениями в рисках для различных округов. Эти границы получены из предположения, что число смертей – это наблюдение, взятое из выборки с биномиальным распределением, размер которой равен количеству взрослого населения округа. Вероятность того, что любой конкретный человек умрет от рака в течение года, составляет 0,000176 (это средний риск смерти по всей стране). Граничные значения включают 95% и 99,8% всех наблюдений соответственно. График такого типа называется воронкообразным и широко используется при мета-анализе.

Для больших выборок точки будут расположены ближе к средней линии. Для малых выборок разброс больше, и точки могут располагаться дальше от среднего.

Предположим, у меня есть монета, и я спрашиваю, с какой вероятностью выпадет орел. Вы отвечаете 50%. Я подбрасываю ее и накрываю, пока никто не увидел результат, и снова спрашиваю, с какой вероятностью будет орел. Это простое упражнение показывает различие между двумя типами неопределенности: стохастической неопределенностью до подбрасывания монеты (когда мы имеем дело с будущим непредсказуемым событием) и эпистемической неопределенностью после подбрасывания монеты (выражением недостатка наших знаний об уже произошедшем событии).

Глава 10. Отвечаем на вопросы и заявляем об открытиях

Нулевая гипотеза – это упрощенная форма статус-кво статистической модели. То, что мы готовы принять, пока не докажем обратное. Как говорил великий британский статистик Роналд Фишер, «нулевая гипотеза в ходе экспериментов никогда не доказывается, но, возможно, опровергается. Можно сказать, что любой эксперимент существует только для того, чтобы дать фактам шанс опровергнуть нулевую гипотезу».

Скрестите руки на груди. У вас сверху левая или правая рука? Я исследовал, связано ли это с тем, мужчина вы или женщина? Вот данные по аспирантам моего курса статистики:

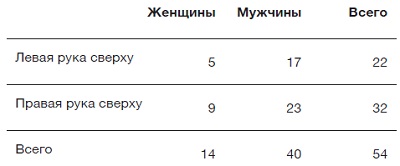
Рис. 8. Таблица сопряженности полов и положения рук при скрещивании для 54 аспирантов (факторная таблица)

У женщин доля «праворуких» (9/14 = 64%) выше, чем у мужчин (23/40 = 57%): наблюдаемая разница между долями составляет 64 — 57 = 7%. Нулевая гипотеза состоит в том, что между скрещиванием рук и полом нет никакой связи, а потому наблюдаемая разница в долях между полами должна равняться 0%. Ключевой вопрос: может ли наблюдаемое отклонение в 7% считаться достаточно большим, чтобы противостоять нулевой гипотезе?

Тест перестановки позволяет ответить на вопрос без сложной математики. Представьте, что все 54 человека выстроились в ряд, сначала 14 женщин, а затем 40 мужчин, и каждому присвоен номер от 1 до 54. Допустим, у каждого есть билет, указывающий, какая рука у него при скрещивании сверху — левая или правая. А теперь вообразите, что все эти билеты смешали в шляпе и раздали присутствующим наугад. Это пример того, каких результатов можно ожидать, если бы нулевая гипотеза была верна, ведь при случайной раздаче скрещивание рук и пол никак не связаны.

Но даже при случайном распределении доля «держащих сверху правую руку» не будет в точности совпадать для мужчин и женщин (просто из-за чистой случайности), и мы можем вычислить наблюдаемую разницу в долях для этой случайной раздачи билетов. Затем мы могли бы повторить процесс, скажем 1000 раз, и посмотреть, какое распределение будет у этой разницы.

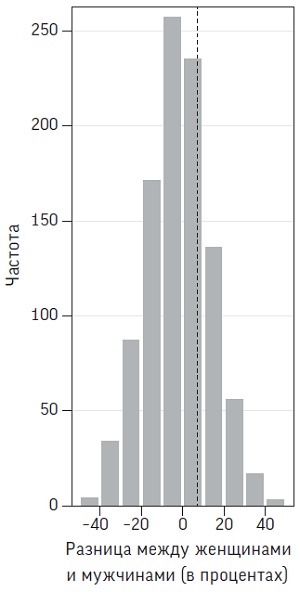
Рис. 9. Эмпирическое распределение разницы между долями женщин и мужчин, которые при скрещивании рук кладут сверху правую руку (для 1000 случайных перестановок). Наблюдаемое различие в пропорциях (7%) обозначено вертикальной пунктирной линией

Мера, характеризующая, насколько близко к центру лежит наблюдаемое значение, – это площадь хвоста распределения. Например, площадь части фигуры, расположенной справа от вертикальной пунктирной линии, составляет 45%. Это число именуется P-значением.

P-значение — это вероятность получить результат, по крайней мере такой же или более экстремальный, чем наблюдаемый, если нулевая гипотеза верна.

Когда P-значение достаточно мало, мы говорим, что результаты статистически значимы.

Алгоритм проверки нулевой гипотезы включает:

Ставим вопрос в терминах нулевой гипотезы H₀.
Выбираем статистику критерия, которая, если ее величина будет достаточно экстремальной, позволит нам поставить под сомнение нулевую гипотезу.
Создаем выборочное распределение этой статистики при условии, что нулевая гипотеза верна.
Проверяем, находится ли наблюдаемая величина в хвостах этого распределения.
Выносим суждение об учете экстремальных величин в одном или обеих хвостах распределения.
Объявляем результат статистически значимым, если P-значение меньше некоторой критической пороговой величины.

Рональд Фишер использовал в качестве удобных порогов значимости P < 0,05 и P < 0,01. И со временем эти значения стали общепринятыми, хотя и остаются произвольно назначенными. Весь этот процесс известен как проверка значимости нулевой гипотезы – Null Hypothesis Significance Testing.

Использование теории вероятностей

В рамках третьего шага мы можем применить компьютерное моделирование, как с тестом перестановки для данных о скрещивании рук на груди. Но удобнее работать с хвостами статистического критерия непосредственно с помощью теории вероятностей, используя гипергеометрическое распределение или классический критерий согласия χ² (хи-квадрат).

Что может быть не так с P-значениями?

Поскольку статистически значимый результат не гарантирует «открытия» в 2016 году Американская статистическая ассоциация предложила шесть принципов, касающихся P-значений (она же альфа α).

P-значения могут указывать на то, насколько несовместимы данные с конкретной статистической моделью.
P-значения не измеряют вероятность того, что изучаемая гипотеза верна или что данные получены исключительно по случайности. Вспомните Байеса! P-значения измеряют вероятность появления экстремальных данных при условии, что нулевая гипотеза верна, но не измеряют вероятность того, что нулевая гипотеза верна, при наличии таких данных.
Научные заключения и процесс принятия решений не должны основываться только на том, переходит ли P-значение определенный порог.
Правильный вывод требует полной отчетности и прозрачности. Только зная план исследования и то, что было на самом деле сделано, можно избежать проблем с P-значениями.
P-значение или статистическая значимость не измеряет величину эффекта или важность результата.
Само по себе P-значение не дает надежного подтверждения модели или гипотезы. Например, P-значение, близкое к 0,05, взятое само по себе, предлагает лишь слабое свидетельство против нулевой гипотезы.

Глава 11. Учимся на опыте – байесовский путь

Томаса Байеса показал, что вероятность может использоваться не только для будущих событий, подверженных случайности, — стохастической неопределенности, но и для реальных событий, известных некоторым людям, просто мы этого пока не знаем, то есть для эпистемической неопределенности.

С байесовской точки зрения для представления нашего личного незнания фактов и чисел удобно использовать вероятности. Байесовские вероятности с необходимостью субъективны — они зависят от наших отношений с окружающим миром, а не являются свойствами самого мира. Такие вероятности должны меняться по мере получения нами новой информации. Это приводит нас ко второму крупному вкладу Байеса — результату, который позволяет постоянно пересматривать текущие вероятности в свете новых доказательств. Он известен как теорема Байеса и фактически предоставляет формальный механизм обучения на опыте.

У вас в кармане три монеты: на одной два орла, на другой две решки, третья обычная. Вы наугад вытаскиваете монету, подбрасываете ее, и выпадает орел. Какова вероятность, что на другой стороне монеты тоже орел? Это классическая задача с эпистемической неопределенностью: как только монета падает после подбрасывания, никакой случайности не остается и любое высказывание о вероятности — всего лишь выражение вашего незнания о другой стороне монеты.

На рис. 10 показано, чего можно ожидать, если проделать такой эксперимент шесть раз. В среднем каждая монета будет выбрана дважды, и каждая из сторон выпадет по разу. Орел выпадает в трех случаях, причем в двух на второй стороне также будет орел. Поэтому вероятность того, что на второй стороне монеты тоже орел, равна 2/3, а не 1/2. По сути, выпадение орла повышает вероятность выбора монеты с двумя орлами, ведь у такой монеты есть два варианта упасть орлом вверх, а у симметричной — только один.

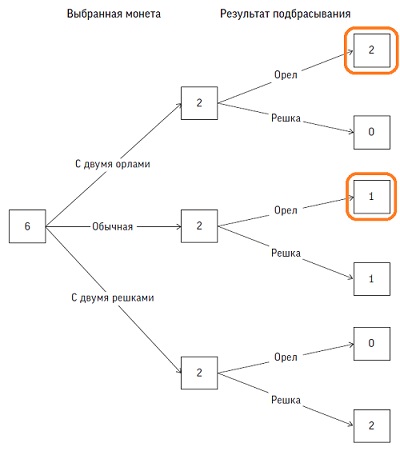
Рис. 10. Дерево ожидаемых количеств для задачи с тремя монетами, показывающее, чего можно ожидать в случае шести экспериментов

Шансы на какое-то событие – это вероятность того, что оно произойдет, деленная на вероятность того, что оно не произойдет. Например, если мы бросаем игральную кость, то шансы на выпадение шестерки равны 1/6 : 5/6 = 1/5 или 1 к 5. Отношение правдоподобия – это вероятность факта при условии гипотезы А, деленная на вероятность факта при условии гипотезы В.

В этих терминах теореме Байеса говорит, что

начальные шансы гипотезы * отношение правдоподобия = конечные шансы для этой гипотезы

Теорема Байеса выглядит обманчиво простой, но на самом деле в ней заключен чрезвычайно мощный способ получения информации из данных.

Глава 12. Когда дела идут не так

Действия, направленные на получение статистически значимых результатов, известны как P-хакинг – изменение результатов исследований с целью добиться нужного P-значения. Такая практика манипулирования данными служит для того, чтобы показать статистические значения, подтверждающие желаемый результат.

Еще одна недобросовестная практика получила название харкинг – выдвижение гипотез после того, как известны результаты (HARKing, hypothesizing after the results are known).

Основная проблема при освещении в СМИ не в откровенной неправде, а в манипуляции и преувеличении путем некорректной интерпретации «фактов»: они могут быть технически верными, но искажены тем, что мы называем «сомнительными методами интерпретации и коммуникации». Вот краткий список способов, как оживить подачу материалов по статистике в СМИ. И те, чья карьера зависит от привлечения читателей, слушателей и кликов, считают многие из этих сомнительных практик вполне оправданными.

Выбирать тексты, которые идут вразрез с текущим общим мнением.
Популяризировать тексты вне зависимости от качества исследований.
Не сообщать уровень неопределенности.
Предполагать причинность, когда наблюдалась всего лишь связь.
Не предоставлять контекст или долгосрочные тенденцииa.
Преувеличивать важность результатов.
Утверждать, что факты поддерживают какую-то установку или линию.
Использовать положительную или отрицательную подачу в зависимости от цели — успокоить или напугать.
Пренебрегать конфликтами интересов и альтернативными точками зрения.
Использовать яркую, но неинформативную графику.
Информировать только об относительных, но не об абсолютных рисках.

Глоссарий

P-значение: мера расхождения между данными и нулевой гипотезой. Пусть имеется нулевая гипотеза Н₀ и критерий Т, большие значения которого указывают на расхождение с Н₀. Предположим, что мы наблюдаем некоторое значение t. Тогда одностороннее P-значение – это вероятность наблюдения не меньшего экстремального значения при условии истинности Н₀, то есть Р(Т ≥ t|Н₀).

Байеса коэффициент: относительное подтверждение, которое дает какой-то набор данных двум альтернативным гипотезам. Для гипотез Н₀, Н₁ и данных х это отношение равно p(x|H₀)/p(x|H₁)

Дилемма смещения – дисперсии: когда для прогноза используется обучение модели, повышение ее сложности в итоге приводит к тому, что у модели уменьшается смещение (в том смысле, что у нее возрастает потенциал для адаптации к деталям базового процесса), но увеличивается дисперсия, поскольку данных для уверенности в параметрах модели оказывается недостаточно. Чтобы избежать переобучения, нужен компромисс.

Критерий независимости хи-квадрат/критерий согласия хи-квадрат: статистический критерий, показывающий степень несовместимости данных с принятой статистической моделью, заключающей нулевую гипотезу (например, величины независимы или имеют определенное распределение). Критерий сравнивает множества каких-то наблюдаемых величин х₁, …, х_m и ожидаемых при нулевой гипотезе величин y₁, …, y_m. Простейший вариант критерия –

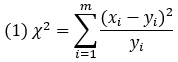
При нулевой гипотезе значение χ² приближенно будет иметь известное χ²-распределение. Это позволяет вычислить соответствующее P-значение.

Мощность критерия: вероятность правильного отклонения нулевой гипотезы при условии справедливости альтернативной гипотезы. Равна 1 — β, где β – вероятность ошибки второго рода для статистического критерия.

Ошибка прокурора: когда малая вероятность факта при условии невиновности ошибочно истолковывается как вероятность невиновности при условии наличия данного факта (Байес).

Переобучение (переподгонка): построение статистической модели, которая чрезмерно адаптирована к тренировочному набору данных, из-за чего ее прогнозные возможности начинают ухудшаться.

Предсказательная аналитика: использование данных в целях создания алгоритмов для прогнозов.

Специфичность: доля «отрицательных» случаев, которые правильно определены при классификации или тестировании. Единица минус специфичность — это доля ложноположительных наблюдений (ошибка первого рода).

Среднеквадратичное (стандартное) отклонение: квадратный корень из дисперсии выборки или распределения. Для хорошо себя ведущих разумно симметричных распределений без длинных хвостов можно ожидать, что подавляющее большинство наблюдений будут лежать в пределах двух стандартных отклонений от выборочного среднего.

Стандартная ошибка: стандартное отклонение выборочного среднего, когда оно рассматривается как случайная величина. Предположим, что Х₁, Х₂, …, Х_n – это независимые одинаково распределенные случайные величины, взятые из распределения со средним μ и среднеквадратичным отклонением σ. Тогда их среднее Y = (Х₁ + Х₂ + … + Х_n)/n имеет среднее μ и дисперсию σ²/n. Стандартное отклонение для Y равно σ/√n и известно как стандартная ошибка. Оценкой будет s/√n, где s – выборочное стандартное отклонение для наблюдаемых величин X.