Функции предсказания в Excel

Excel, как универсальный табличный редактор, давно и неплохо справляется с большинством задач прогнозирования (см. список литературы в конце заметки). Однако, не всегда вычисления в Excel являются простыми и понятными. И вот в версии 2016 года разработчики Microsoft добавили семейство функций ПРЕДСКАЗ (FORECAST), которые позволяют в несколько кликов решать большой круг задач прогнозирования на основе экспоненциального сглаживания.

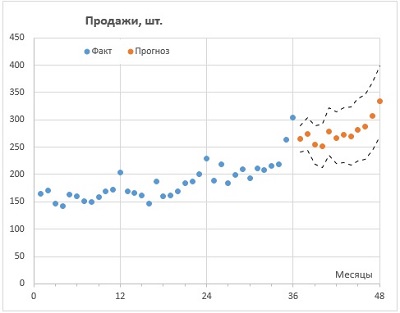
Рис. 1. Прогнозирование продаж в Excel с помощью семейства функций ПРЕДСКАЗ

Скачать заметку в формате Word или pdf, примеры в формате Excel

Об экспоненциальном сглаживании

Экспоненциальное сглаживание также известно, как метод ETS: ошибки (Errors), тренд (Trend), сезонный фактор (Seasonal). Для составления прогноза используются все исторические данные, но коэффициенты, определяющие вклад, убывают в прошлое по экспоненте (отсюда и название). Это позволяет, с одной стороны, чутко реагировать на свежие данных, с другой стороны, сохранять информацию об историческом поведении всего временного ряда. Если данным присущ тренд, он вычисляется в каждой точке данных (а не на основе регрессии всего временного ряда). Наконец, с помощью автокорреляции в данных выявляется сезонность.

Преимущество модели в том, что она не использует никаких предположений относительно характера тренда (или его отсутствия) и периодичности сезонных колебаний (или их отсутствия). Все коэффициенты в модели подбираются на основе минимизации суммы квадратов ошибок, то есть, разности между прогнозом на исторических данных и самих данных. Если вас интересует, как это происходит, рекомендую работу Формана (см. список литературы).

Собственно, оптимизируются три коэффициента:

α – разброс относительно среднего

γ – тренд

δ – сезонность

Разработчики Microsoft не предоставили пользователям возможность влиять на выбор коэффициентов, за исключением периода сезонности (об этом ниже).

Обзор функций семейства ПРЕДСКАЗ

В Excel представлено 5 функций:

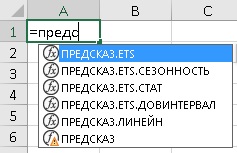
Рис. 2. Семейство функций ПРЕДСКАЗ в Excel

ПРЕДСКАЗ.ETS рассчитывает будущее значение на основе существующих (ретроспективных) данных методом экспоненциального сглаживания. Т.е., дает прогноз одним числом.

ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ возвращает доверительный интервал для прогнозной величины. Доверительный интервал следует отложить по обе стороны от среднего значения. Вместе с ПРЕДСКАЗ.ETS позволяет построить «коридор» прогноза.

ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ возвращает длину повторяющегося фрагмента, обнаруженного в заданном временном ряду. Например, 12, если исторические данные представляют из себя продажи за месяц.

ПРЕДСКАЗ.ETS.СТАТ возвращает восемь статистических значений, являющихся результатом прогнозирования временного ряда. Вряд ли вы будете использовать эту функцию. Она нужна для более тонкого исследования параметров прогнозной модели.

ПРЕДСКАЗ.ЛИНЕЙН вычисляет будущее значение с помощью линейной регрессии исторических данных. До версии 2016 в Excel вместо семейства функций была единственная функция ПРЕДСКАЗ, которая работала также, как и ПРЕДСКАЗ.ЛИНЕЙН. Функция ПРЕДСКАЗ оставлена для обратной совместимости, но скоро перестанет поддерживаться. Далее в заметке ПРЕДСКАЗ.ЛИНЕЙН не рассматривается, так как не относится к функциям, использующим алгоритм экспоненциального сглаживания.

ПРЕДСКАЗ.ETS

Синтаксис:

В качестве примера рассмотрим месячный пассажиропоток в аэропорту (пример от MS). Исторические данные были собраны за период с января 2009 по декабрь 2912 г.

Рис. 3. Исторические данные

Продолжим временную шкалу еще на год, и создадим столбец для прогноза. Обычно прогноз располагают в отдельном столбце для того, чтобы при построении графика представить исторические и прогнозные значения разными линиями.

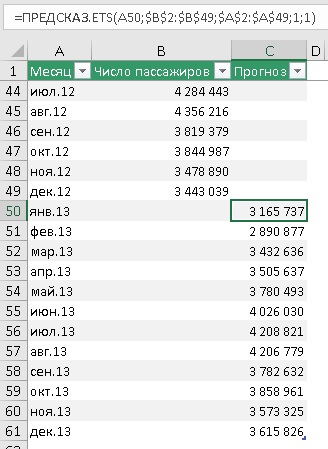
Рис. 4. Прогнозные значения на основе функции ПРЕДСКАЗ.ETS

Подробнее о формуле в ячейке С50:

=ПРЕДСКАЗ.ETS(A50;$B$2:$B$49;$A$2:$A$49;1;1)

Первый аргумент – целевая_дата = А50 – янв.13, т.е., в ячейке С50 ищется прогноз пассажиропотока для января 2013 г. Ссылка относительная, что позволит при протягивании функции вниз по столбцу ссылаться на новое значение: в С51 – на А51, в С52 – на А52 и т.д.

Второй аргумент – значения = $B$2:$B$49. Здесь расположены исторические данные пассажиропотока. Ссылка абсолютная, чтобы при протягивании формулы ячейки, на которые ссылаются не изменились.

Третий аргумент – временная_шкала = $A$2:$A$49. Здесь расположены даты временной шкалы или номера периодов. Важно чтобы они отстояли друг от друга на фиксированный интервал. Если интервал не будет фиксированным, Excel всё еще будет исходить из гипотезы, что интервал фиксированный, а некоторые данные пропущены. Как обрабатываются такие ситуации описано ниже. Сортировать массив по значениям временной шкалы не обязательно, так как ПРЕДСКАЗ.ETS сама отсортирует данные прежде, чем выполнить расчеты.

Четвертый аргумент – [сезонность] = 1. Это необязательный аргумент. Значение по умолчанию равно 1. Для него Excel автоматически определяет сезонность и использует положительные целые числа в качестве длины сезонного шаблона. Значение 0 предписывает не использовать фактор сезонности, в результате чего прогноз будет линейным. Если для этого параметра задано положительное целое число, алгоритм использует его в качестве длины шаблона сезонности. Например, вы знаете, что сезонность равна 4 (квартальная периодичность), но предполагаете, что она слабая, и автоматический алгоритм Excel может ее не выявить, и будет считать, что сезонности нет. Для начала я рекомендовал бы использовать значение по умолчанию.

Пятый аргумент – [заполнение_данных] = 1. Это необязательный аргумент. Хотя временная шкала требует постоянный шаг между точками данных, FORECAST.ETS поддерживает до 30% отсутствующих данных и автоматически настраивает их. 0 указывает, что алгоритм учитывает отсутствующие точки в качестве нулей. Если задано значение 1 (вариант по умолчанию), функция определяет отсутствующие значения как среднее между соседними точками.

Шестой аргумент – [агрегирование] – в нашем примере опущен. Это необязательный аргумент. Он нужен, если даты временной шкалы или номера периодов содержат дубли. Функция ПРЕДСКАЗ.ETS выполнит агрегирование точек с одинаковой меткой времени. Параметр агрегирования — это числовое значение, определяющее способ агрегирования нескольких значений с одинаковой меткой времени. Для значения по умолчанию 0 используется метод СРЗНАЧ; также доступны варианты СУММ, СЧЁТ, СЧЁТЗ, МИН, МАКС и МЕДИАНА.

ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ

Синтаксис:

Здесь один новый аргумент – вероятность. Он необязательный. И принимает значения от 0 до 1 (не включительно). Например, для значения 95% выполняется расчет доверительного интервала, в который с вероятностью 95% попадут прогнозные точки. Функция ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ возвращает значение в тех же физических единицах, что и ПРЕДСКАЗ.ETS. Например, 50±8. Здесь 8 – доверительный интервал, возвращаемый функцией ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ. Он откладывается от среднего прогнозного значения по обе стороны.

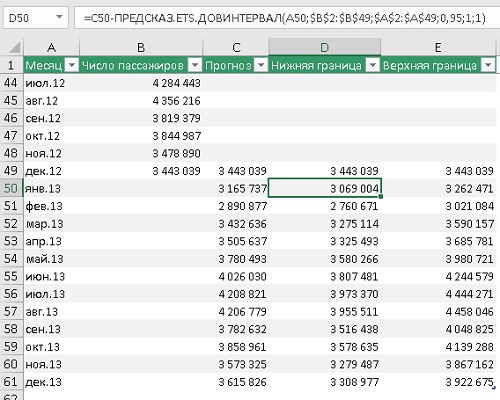
Рис. 5. Расчет границ коридора прогноза

Теперь на основании расчета среднего прогноза, возвращаемого функцией ПРЕДСКАЗ.ETS и границ коридора, возвращаемого формулами…

=C50±ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ(A50;$B$2:$B$49;$A$2:$A$49;0,95;1;1)

… можно построить график прогноза с доверительными границами:

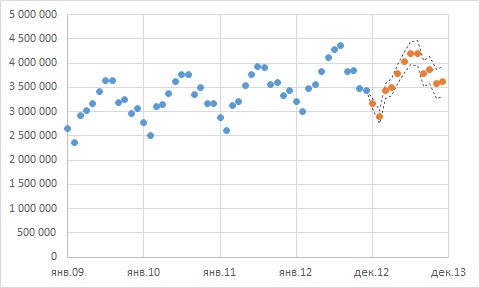
Рис. 6. Исторические и прогнозные данные пассажиропотока с 95%-ными доверительными границами

Благодаря тому, что исторические данные демонстрируют четкие закономерности, прогнозные границы получились довольно узкими.

ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ

Синтаксис:

Здесь нет новых для нас аргументов. В простейшем случае функция ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ принимает исторические данные и временную шкалу, и возвращает целое число, равное сезонности. В нашем примере – 12:

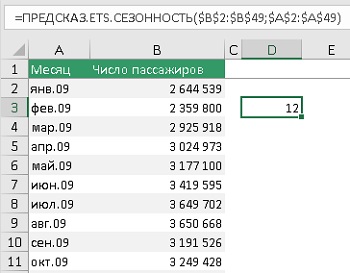
Рис. 7. Значение сезонности

ПРЕДСКАЗ.ETS.СТАТ

Синтаксис:

Новый аргумент один – тип_статистики. Является обязательным. Принимает целые значения от 1 до 8. Я использовал вложенную функцию ПОСЛЕД(8), которая задала массив целых чисел: 1, 2, … , 8. И функция ПРЕДСКАЗ.ETS.СТАТ отработала как функция динамического массива, создав столбец из 8 значений статистики:

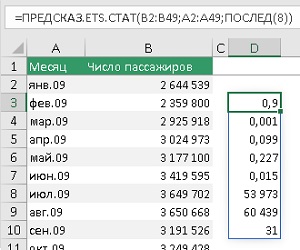
Рис. 8. Статистики экспоненциального сглаживания

Первый параметр – альфа = 0,9. Чем он больше, тем больше вес более новых точек данных. Не следует путать коэффициенты, оптимизируемые в модели ETS (α, γ и δ), и значения, возвращаемые функцией ПРЕДСКАЗ.ETS.СТАТ. Это – о разном. Второй параметр – бета = 0,001. Возвращает значение параметра тренда: чем оно больше, тем больше вес более нового тренда. Третий параметр – гамма. Возвращает значение параметра сезонности: чем оно больше, тем больше вес более нового сезонного периода. С четвертого по седьмой параметр – это различные показатели точности прогноза. Восьмой параметр – величина шага, определенную во временной шкале ретроспективных значений. В нашем случае 31 день.

Лист прогноза

Вишенкой на торте является кнопка на ленте, доступная по меню Данные –> Прогноз –> Лист прогноза. Эта кнопка на основе исторических данных создает новый лист Excel с колонками прогноза, границ доверительного интервала, статистикой модели и довольно сносной диаграммой. Итак, встаньте курсором на любую клетку умной таблицы с исходными данными (как на рис. 3) и кликните Лист прогноза. Откроется окно Создание листа прогноза.

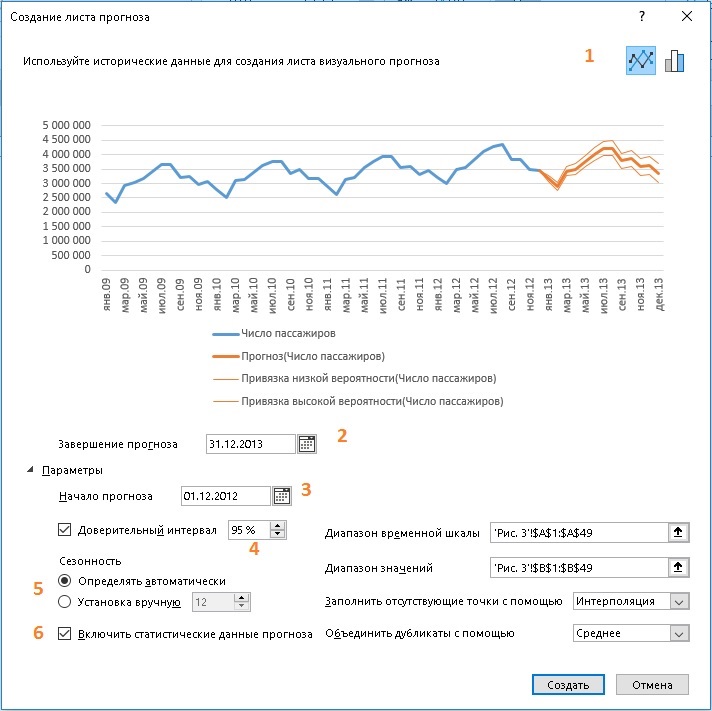
Рис. 9. Настройка параметров листа прогноза

Здесь (1) можно выбрать тип диаграммы: график или гистограмма, (2) задать период прогнозирования, (3) выбрать на временной шкале начало прогноза; (4) выбрать величину доверительного интервала, (5) использовать параметр сезонности (число), определяемый функцией ПРЕДСКАЗ.ETS автоматически, или установить сезонность принудительно, (6) указать, выводить ли статистику прогнозной модели.

Если выбрать дату начала прогноза внутри временной шкалы исторических данных, то прогноз для каждой точки будет использовать только данные, предшествующие ей (это называется «ретроспективным прогнозированием»).

Если начать прогнозирование перед последней точкой, можно получить оценку точности прогноза, сравнив прогнозируемый ряд с фактическими данными. Но если начать прогнозирование со слишком ранней даты, построенный прогноз может отличаться от созданного на основе всех статистических данных. При использовании всех статистических данных прогноз будет более точным.

Если в ваших данных прослеживаются сезонные тенденции, то рекомендуется начинать прогнозирование с даты, предшествующей последней точке статистических данных.

Если вы хотите задать сезонность вручную, не используйте слишком короткие ряды исторических значений. Нужно как минимум два полных цикла статистических данных. На коротких исторических данных лучше довериться автоматическому определению сезонности. Если алгоритм не выявит сезонность, прогноз примет вид линейного тренда.

Настроив параметры в окне Создание листа прогноза, нажмите Создать. В нашем примере Excel создаст новый лист, расположенный слева (перед) листом с историческими данными:

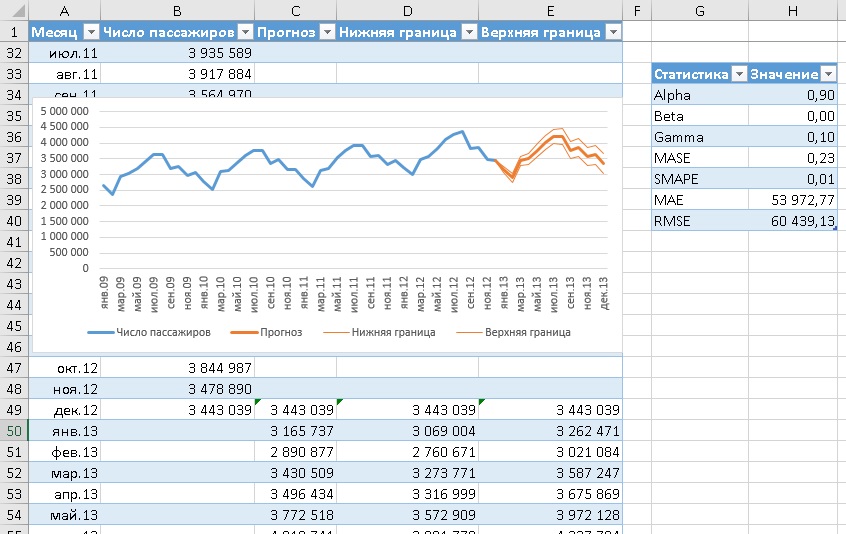
Рис. 10. Лист прогноза

Литература

Джон Форман. Много цифр: Анализ больших данных при помощи Excel. Глава 8. Прогнозирование на основе экспоненциального сглаживания.  В заметке на сквозном примере в Excel рассмотрено простое экспоненциальное сглаживание, ПЭС (simple exponential smoothing, SES); экспоненциальное сглаживание Холта с корректировкой тренда; анализ автокорреляций в данных; мультипликативное экспоненциальное сглаживание Холта-Винтерса; построение доверительного интервала прогноза методом Монте-Карло.

Левин и др. Статистика для менеджеров. Глава 15. Анализ временных рядов. В заметке: что такое временные ряды; компоненты классической мультипликативной модели временных рядов; сглаживание временных рядов; скользящее среднее; экспоненциальное сглаживание; вычисление трендов с помощью метода наименьших квадратов; модели линейной, квадратичной и экспоненциальной регрессии; выбор модели на основе разностей первого и второго порядка; вычисление тренда с помощью авторегрессии; прогнозирование временных рядов на основе сезонных данных; ловушки, связанные с анализом временных рядов; индексы.

Прогнозирование спроса и продаж. Записки дилетанта. В заметке: общие рассуждения о прогнозировании; постановка задачи прогнозирования; наивные методы прогнозирования (простое среднее, скользящее среднее, взвешенное скользящее среднее); простое экспоненциальное сглаживание; составляющие прогнозной модели (тренд, сезонность); классическая сезонная декомпозиция; экспоненциальное сглаживание с учетом тренда и сезонности (метод Холта-Винтерса); прогнозирование редких продаж (метод Кростона и метод Виллемейна); метод Кростона и страховой запас; функция распределения спроса.