Недавно я прочитал книгу Ричард Талера Новая поведенческая экономика. Книга мне очень понравилась. Она, в частности, опирается на труды Амоса Тверски и Даниэля Канемана, идеи которых мне очень симпатичны (см., например, Канеман, Словик, Тверски. Принятие решений в неопределенности: Правила и предубеждения и Даниэль Канеман. Думай медленно… решай быстро). Талер является одним из родоначальников экономического изучения обычных (реальных) людей, а не полностью рациональных и осведомленных агентов, как это принято в традиционной экономике. Поэтому один из разделов книги Талера я решил опубликовать почти полностью.
Скачать заметку в формате Word или pdf
Глава 21. Конкурс красоты
Сложно передать словами, насколько скептически люди относились к изучению поведенческой экономики финансовых рынков. Можно говорить о странных поступках, совершаемых обычными потребителями, но финансовые рынки считались местом, где неразумное поведение не смогло бы повлиять на биржевой курс. Большинство экономистов полагали – и это была отличная исходная гипотеза, – что, даже если некоторые люди совершали ошибки в обращении со своими деньгами, другие умные люди могли скорректировать цены таким образом, чтобы рыночный курс никак не страдал. Теория эффективного рынка считалась среди профессионалов доказанной. На самом деле, когда я впервые начал изучать психологию финансовых рынков в начале 1980-х, Майкл Дженсен, мой коллега по бизнес школе в Рочестере, написал: «Я считаю, что нет никакого другого исходного положения в экономике, которое имело бы более солидные эмпирические доказательства, чем гипотеза эффективного рынка».
Термин «гипотеза эффективного рынка» придумал экономист Юджин Фама из Университета Чикаго. Фама – живая легенда не только для финансовых экономистов, но также и для Высшей католической школы Малден, что возле Бостона, штат Массачусетс, где его выбрали для галереи славы легкой атлетики – это стало одним из самых дорогих его сердцу достижений. После окончания местного Университета Тафтса, где он специализировался по направлению «французский язык», Фама отправился в университет Чикаго, чтобы продолжить образование. Его блистательный талант был настолько очевиден, что университет предложил ему работу на факультете сразу по окончании (небывалый случай), и он уже никогда не покидал этот университет. Недавно в Школе бизнеса им. Бута при Чикагском университете отметили пятидесятую годовщину работы Фама.
Фама и Мертон Миллер были ведущими финансовыми экономистами в Чикаго, пока не умер Мертон, и до сего дня Фама продолжает преподавать первый курс, который слушают все аспиранты финансисты, чтобы не сомневаться, что они сделают правильный старт.
Гипотеза эффективного рынка состоит из двух компонентов, которые некоторым образом взаимосвязаны, но концептуально различаются. Один компонент относится к рациональности цен; другой касается вопроса, возможно ли переиграть рынок.
Первый компонент я называю «корректная цена», используя термин, который впервые услышал от Клиффа Смита, коллеги из университета Рочестера, который описывал рынок ценных бумаг. Из аудитории доносился рев Клиффа с сильным южным акцентом: «Цена корректна»! По сути, идея состоит в том, что любой актив продается весь за свою «объективную» стоимость. Если рациональная стоимость компании составляет 100 000 000 $, тогда ее акции будут торговаться так, что рыночная капитализация фирмы будет равна 100 000 000 $. Этот принцип, работает и для индивидуальных ценных бумаг, и в целом для рынка.
На протяжении многих лет финансовые экономисты жили с ложным чувством защищенности, которое было основано на мысли о том, что компонент «корректная цена» гипотезы эффективного рынка невозможно проверить напрямую, – это одна из причин, почему мы говорим о гипотезе. Объективная стоимость, по утверждению экономистов, не поддается наблюдению. В конце концов, кто должен определять, какой является рациональная, или корректная, цена для таких компаний, как «General electric», «Apple» или «Dow Jones Industrial Average»? Нет лучшего способа обосновать состоятельность теории, чем считать, что ее невозможно проверить. Фама не заостряет внимания на этом компоненте теории, хотя во многих аспектах это более чем просто важная часть гипотезы эффективного рынка. Если цены «корректны», тогда никакие ценовые пузыри попросту невозможны, опровержение этого компонента теории стало бы сенсацией.
Большинство первых научных исследований, посвященных теории эффективного рынка, фокусируются на втором ее компоненте, который я назову принципом «бесплатных обедов не бывает», – идея состоит в том, что нет никакого способа победить рынок. Если говорить конкретно, этот принцип утверждает, что из-за отражения общедоступной информации на текущем биржевом курсе невозможно с уверенностью предсказать изменение цен и заработать на этом.
Аргумент в защиту этой гипотезы интуитивно кажется убедительным. Предположим, бумаги продаются по цене 30 $ за акцию, и я знаю наверняка, что скоро они будут стоить 35 $ за акцию. В этом случае я смог бы легко разбогатеть, купив эти акции по цене ниже 35 $, а затем перепродав их, когда мой прогноз сбудется. Но, разумеется, если информация, которую я использую, чтобы сделать этот прогноз, является публичной, тогда маловероятно, что я буду единственным, обратившим на это внимание. Как только информация становится доступной, любой, кто владеет ею, начнет покупать акции и цена практически мгновенно вырастет до 35 $, что означает упущение возможности выгодной сделки. Эта логика кажется убедительной, и первые проверки теории подтвердили ее. В некотором смысле Майкл Дженсен в своей диссертации представил самый убедительный анализ. Он показал, что профессиональные финансовые менеджеры в лучшем случае могут рассчитать средний рыночный курс, этот факт остается актуальным по сей день. Если профессионалы не могут победить рынок, то кто может?
Меня немного удивляет, что гипотеза эффективного рынка была формально выдвинута только в 1970-х, учитывая, что она исходит из тех же самых принципов оптимизации и равновесия, которые были сформулированы в других областях экономики значительно раньше. Одно из возможных объяснений состоит в том, что финансовая экономика как область знания развивалась немного медленнее, чем другие области экономики.
Финансы на сегодняшний день – это высоко уважаемая область экономики, и многочисленные Нобелевские премии были присуждены экономистам, чья основная работа относилась к сфере финансов, включая недавнюю награду 2013 года. Но это не всегда было так, хотя некоторые интеллектуальные гиганты из этой сферы, такие как Кеннет Эрроу, Пол Самуэльсон и Джеймс Тобин, сделали важный вклад в развитие финансовой экономики в 1950-х и 1960-х, финансы не были одним из основных направлений на факультетах экономики, и вплоть до 1970-х в бизнес школах финансы были чем-то неизведанным с точки зрения науки. Курсы по финансам часто были похожи на бухгалтерские курсы, где студенты учились тому, как лучше вычислить, в какие акции стоит вкладывать деньги. Мало что было сделано в области теории, и еще меньше – в области эмпирических исследований.
Современная история финансовой экономики началась с имен таких теоретиков, как Гарри Маркович, Мертон Миллер и Уильям Шарп, но эта область как академическая дисциплина возникла благодаря двум ключевым событиям: снижению цен на вычислительные ресурсы и открытию доступа к большим данным. Прорыв в области данных произошел в университете Чикаго, где бизнес школа получила грант в размере 300 000 $ на разработку базы данных по курсу ценных бумаг начиная с 1926 года. Так появился Центр исследований котировок ценных бумаг известный как CRSP (произносится «крисп»).
Первая база данных была выпущена Центром в 1964 году, и немедленно начались исследования, причем местные исследователи из Университета Чикаго были в ряду первых. Главными среди них были Миллер и Фама, а также группа одаренных студентов выпускников, включая Майкла Дженсена, Ричарда Ролла (выдающийся исследователь и профессор Калифорнийского университета в Лос-Анджелесе) и Майрона Шоулза, соавтора модели ценообразования опционов Блэка–Шоулза. Исследования быстро развивались. К 1970 году теоретическая и эмпирическая базы, подтверждающие гипотезу эффективного рынка, уже были достаточно хорошо сформированы, так что Фама смог опубликовать солидный обзор литературы, остававшегося на протяжении многих лет библией эффективного рынка. Всего лишь восемь лет спустя после того, как Фама задокументировал основные постулаты гипотезы эффективного рынка, в одной из публикаций Дженсена появилась фраза о том, что гипотеза эффективного рынка доказана. Ирония состоит в том, что эта фраза появилась в предисловии к специальному выпуску журнала по финансовой экономике, который был посвящен аномалиям, то есть собранные в нем статьи описывали исследования об отклонениях от гипотезы эффективного рынка.
Уверенность Дженсена и остальных в гипотезе эффективного рынка была, возможно, основана во многом на убедительной логике самой идеи, а также на эмпирических данных. Кроме того, 1970-е были временем, когда похожая революция происходила в области макроэкономики. Модели, основанные на рациональных допущениях, пользовались огромной популярностью, а популярность кейнсианской экономики среди научных экономистов падала. Возможно, по этой причине студенты больше не читали Кейнса. Это чрезвычайно печально, ведь, если бы Кейнс был жив, он мог бы добавить беспристрастности в эти дебаты. Он был истинным пионером в области поведенческих финансов.
В наши дни Кейнса вспоминают в основном за его вклад в макроэкономику и особенно за его противоречивое утверждение о том, что правительство должно использовать налоговую политику для стимулирования спроса в период рецессии или депрессии. Независимо от того, что вы думаете о кейнсианской макроэкономике, было бы неосмотрительно упустить из виду его рассуждения о финансовых рынках. Для меня самая любопытная глава из его известной книги Общая теория занятости, процента и денег посвящена именно этому предмету. Наблюдение Кейнса основаны частично на его богатом опыте инвестора. На протяжении многих лет он успешно управлял портфелем своего колледжа в Кембридже, где был лидером в продвижении идеи инвестирования эндаумента[1] в акции.
Кейнс считал, что эмоции, или то, что он называл «животный дух», играли важную роль в процессе принятия индивидом решений, включая решения об инвестициях. Любопытно, что Кейнс считал рынки более «эффективными», выражаясь современным языком, в свои первые дни в начале XX века, когда финансовые менеджеры являлись собственниками большинства акций компании и знали, сколько стоила эта компания. Он полагал, что, когда акции получили большее распространение, «доля истинного знания в оценке инвестиций теми, кто являлся их собственником или обладал правом их покупки… значительно снизилась».
Когда в середине 1930-х Кейнс писал «Общую теорию», он уже сделал вывод о том, что рынки немного сошли с ума. «Изо дня в день колебания доходности по существующим инвестициям, которые, со всей очевидностью, лишь эфемерный и малозначимый фактор, становятся все более частым явлением, и даже абсурдными в том, как они влияют на рынок». Чтобы подкрепить это утверждение, Кейнс обращает внимание на тот факт, что акции производителей льда выше в цене в летние месяцы, когда продажи также на подъеме. Этот факт удивителен, потому что в условиях эффективного рынка рыночный курс отражает долгосрочную стоимость компании, которая не должна зависеть от теплой погоды летом и холодной погоды зимой. Настолько предсказуемая сезонная модель рыночного курса строго запрещается в рамках гипотезы эффективного рынка.
Кейнс также скептически относился к тому, что профессиональные фондовые менеджеры могут выполнять роль «умных денег», на которые полагаются защитники гипотезы эффективного рынка в выравнивании ситуации на рынке. Кейнс, наоборот, считал, что профессионалы сами скорее склонны к иррациональному поведению, чем к его предотвращению. Одна из причин состояла в том, что «плыть против течения» всегда довольно рискованно. «Общепризнанная истина заключается в том, что для сохранения репутации лучше иногда ошибаться, чем беспрестанно быть правым» (Насим Талеб, основываясь на глубоком понимании риска, применил выигрышную стратегию… на длинном отрезке времени, но денег дождаться окончания этого отрезка не хватило; см. Малкольм Гладуэлл о Нассиме Николасе Талебе). Кейнс полагал, что фондовые менеджеры играли в сложную игру на угадывание. Он сравнил выбор лучших акций с обычной конкуренцией в финансовой среде Лондона 1930-х, в которой доминировали мужчины… Они выбирали самые хорошенькие лица из пачки фотографий.
Профессиональное инвестирование можно сравнить с конкурсами красоты, которые проводит газета, где участникам предлагается выбрать шесть самых красивых лиц из сотни фотографий, при этом приз получает тот, чей выбор почти соответствует средним предпочтениям всех участников в целом: таким образом каждый участник должен выбрать не те лица, которые он лично считает самыми красивыми, а те, которые, по его мнению, с наибольшей вероятностью привлекут внимание его соперников, и все участники рассматривают свою задачу с той же самой позиции. Цель состоит не в выборе самых красивых лиц согласно собственному суждению и даже не в выборе красивых лиц по общему усредненному мнению. Здесь речь идет уже о третьем уровне сложности, где мы тратим свои умственные способности на выяснение того, каким в среднем будет среднее мнение. Я полагаю, существуют также те, кто практикует четвертый, пятый и более высокий уровень сложности игры на угадывание.
На мой взгляд, аналогия с конкурсом красоты, которую провел Кейнс, является самым точным описанием того, как работают финансовые рынки, а также того, как поведенческие факторы играют здесь ключевую роль, хотя, возможно, во всем этом довольно сложно разобраться. Чтобы понять суть этой аналогии и оценить ее тонкость, попробуйте решить следующую задачку.
Загадайте число от 0 до 100 так, чтобы загаданное вами число было как можно ближе или равнялось двум третям от средней величины чисел, которые загадывают все те, кто решает такую задачку.
Чтобы помочь вам в решении, предположим, что есть три игрока, которые загадали числа 20, 30 и 40. Среднее значение загаданных чисел равняется 30, две трети от тридцати – 20, значит, тот игрок, который загадал 20, выиграл. Загадайте число перед тем, как читать дальше. Нет, действительно, попробуйте: вам еще больше понравится остальная часть этой заметки, если вы попробуете сами сыграть в эту игру.
Хотели бы вы задать вопрос, перед тем как загадать число? Если так, то какой? Мы вернемся к нему через минуту. А теперь давайте представим, как может рассуждать участник этой игры.
Представим себе игрока, которого я называю мыслителем нулевого уровня. Он говорит: «Не знаю, похоже, здесь какая-то математическая задачка, а я не люблю математику, особенно проблемы со словами. Наверное, я выберу число наугад». Большинство тех, кто выбирает число от 0 до 100 наугад, загадывают 50.
Как насчет мыслителя первого уровня? Он скажет себе: «Остальные не очень любят напрягать мозг, наверное, они выберут число наугад, среднее значение будет равно 50, поэтому мне следует выбрать 33, потому что это две трети от 50».
Мыслитель второго уровня подумает примерно так: «Остальные игроки в большинстве своем – это мыслители первого уровня, они считают, что остальные умом не блещут, поэтому загадают 33. Следовательно, я выбираю 22».
Мыслитель третьего уровня думает: «Большинство игроков поймут, как работает механизм вычисления в этой игре, поэтому решат, что большинство выберут число 33. Значит, сами они решат выбрать 22, так что я выбираю 15».
Конечно, сложно поставить точку в этой цепочке размышлений. Вы хотите поменять загаданное вами число?
Вот еще одна загадка для вас: каково было бы равновесие Нэша для этой ситуации? Названное по имени Джона Нэша, который является героем известной книги (а также фильма биографии) «Игры разума», равновесие Нэша для этой игры возникнет в ситуации, когда участники загадают число, которое никто не захочет менять. И это число – ноль. Чтобы понять почему, предположим, что все загадали число 3. Тогда в средняя величина от загаданных чисел равна трем и вам нужно загадать число, которое равняется двум третям от этого числа, т.е. два. Но если все загадают число 2, тогда вам нужно будет загадать 1,33 и так далее. Только в том случае, если все участники загадают ноль, никто не захочет менять загаданное число.
Может быть, теперь у вас назрел вопрос, который стоило бы задать перед тем, как объявлять свое загаданное число: кто такие другие игроки и каковы их знания в области математики и теории игр? Если вы играете в местном баре, особенно поздно вечером, то другие игроки, вероятно, не станут сильно напрягать мозг, поэтому вы можете загадать число 33 или что-то близкое. И только если вы находитесь среди участников конференции, посвященной теории игр, вам нужно будет загадать число, близкое к нулю.
Давайте теперь посмотрим, какое отношение эта игра имеет к конкурсу красоты, который описал Кейнс. Формально условия идентичные. В игре по угадыванию чисел необходимо угадать, что думают другие люди о том, что думают другие, точно так же, как и в конкурсе Кейнса. На самом деле «игру по угадыванию чисел» экономисты обычно называют «конкурсом красоты».
Эта чудесная игра впервые стала предметом исследования в рамках эксперимента немецкого экономиста Розмари Нагел, которая преподает в Университете Помпеу Фабра в Барселоне. Благодаря газете «Файнэншл таймс» в 1997 году у меня появилась возможность воспроизвести полученные ею результаты уже в рамках крупномасштабного эксперимента. Однажды меня попросили написать короткую статью о поведенческой экономике финансовых рынков для газеты «Файнэншл таймс», и я захотел воспользоваться игрой по угадыванию чисел, чтобы пояснить идею Кейнса про конкурс красоты. Затем у меня появилась идея получше: что, если за несколько недель до выхода моей статьи провести среди читателей газеты эту игру в формате конкурса? Таким образом, я смог бы представить свежие данные, полученные на основе опроса читателей «Файнэншл таймс», в своей статье. Согласие со стороны газеты было получено, а компания «Британские авиалинии» предложила разыграть в качестве приза два билета бизнес классом из Лондона в США. Исходя из того, что вам теперь уже известно, какое, по вашему мнению, число загадали читатели?
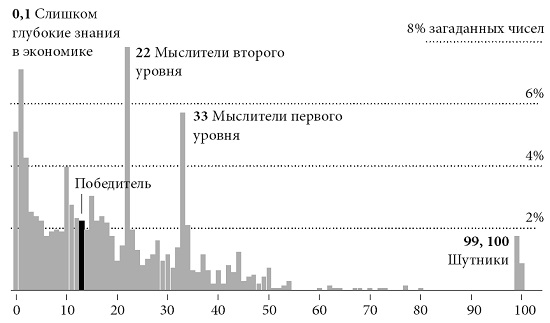
Правильный ответ 13. Распределение полученных ответов показано на рисунке. Как вы видите, многие читатели «Файнэншл таймс» оказались достаточно сообразительны, чтобы вычислить, что ноль обеспечивает равновесие Нэша для этой игры, но им все же не хватило ума додуматься, что это не будет правильным ответом. Несколько человек также загадали число один, допуская возможность, что найдутся болваны, которые не смогут разобраться в сути игры и тем самым поднимут значение средней величины ответов выше нуля.
Многие мыслителя первого и второго уровней загадали 33 и 22. Но как насчет загадочных чисел 99 или 100; о чем думали эти ребята? Оказывается, все эти ответы поступили от студентов одного общежития Оксфордского университета. По правилам, каждый участник мог прислать только один ответ, но нашелся кто-то достаточно ловкий и заполнил открытки от имени всех своих соседей. Мне и моим ассистентам выпала нелегкая задача решить, можно ли засчитывать эти ответы. В итоге мы решили оставить открытки, раз они были подписаны разными именами, таким образом правильный ответ сместился с 12 на 13. К счастью, никто из этих ребят не загадал число 13.
Рис. Ответы читателей «Файнэншл таймс» в игре «Конкурс красоты»
Мы попросили участников коротко описать ход своих рассуждений и потом использовали эти пояснения в качестве решающего аргумента. Это принесло нам дополнительный бонус. Некоторые из этих объяснений были очень разумны. Среди ответивших был один поэт, который загадал ноль и прислал ответ в стихах: «Бихевиористы изучают людей, читателей «Файнэншл таймс», а значит, умных людей, мы знаем правила и будем сражаться по чести, поэтому выбираем число бесконечности». Был один представитель Тори, который, решив, что мир нельзя считать рациональным, загадал 1: «Правильным ответом должен быть ноль… но победили Лейбористы».
Студент, загадавший число 7, так объяснил свой выбор: «Потому что мой отец разбирается в вычислении среднего значения для чисел и рынков, и его ответ был 10». Обратите внимание, что – это свойственно молодежи – парень переоценил своего отца. Если бы он переместил своего родителя на один уровень ниже среднего игрока, то мог бы выиграть!
Наконец, еще один поэт загадал 10: «Число больше 67 загадают дураки; число больше 45 означает, что надо снова в школу идти. Случайное число между 45 и единицей – это 23. Логика подсказывает 15, и я выбираю 10».
Как показывают ответы читателей «Файнэншл таймс», при разном уровне сложности игры на угадывание аналогия, проведенная Кейнсом между конкурсом красоты и тем, как работают профессиональные инвестиционные менеджеры, все еще очень актуальна. Многие инвесторы называют себя «дисконтными менеджерами», имея в виду, что они стараются покупать дешевые ценные бумаги. Другие называют себя «менеджерами роста», имея в виду, что покупают акции, которые быстро вырастут в цене. Но, разумеется, никто не стремится покупать дорогие ценные бумаги, так же, как и те акции, которые упадут в цене. Так что же на самом деле делают все эти менеджеры? Они стараются скупить акции, которые вырастут в цене, – или, другими словами, те акции, которые, по их мнению, другие инвесторы вскоре оценят выше, полагаясь, в свою очередь, на свои собственные оценки того, как другие оценят в будущем эти бумаги.
Нет ничего предосудительного в покупке акций, которые сегодня рынок не оценивает слишком высоко, при условии, что рано или поздно остальные игроки на рынке также придут к мнению, что эти бумаги будут стоить дороже. Вспомните известное изречение Кейнса: «В конечном счете все мы умрем». Этот конечный счет для портфельного инвестора измеряется всего лишь несколькими годами – возможно, даже несколькими месяцами!
См. также Кейнсианский конкурс красоты.
[1] Эндаумент — сформированная за счёт пожертвований часть имущества некоммерческой организации, переданная в доверительное управление управляющей компании для получения дохода, используемого для финансирования уставной деятельности некоммерческих организаций.

Спасибо, очень познавательно! Недавно наткнулся на Ваш ресурс и, признаться честно, очень рад этому! Спасибо, что продвигаете знания