На русском языке вышла еще одна книга основоположника теории ограничений Элияху Голдратта[1] – «Я так и знал!» М.: Издательство «Манн, Иванов и Фербер». 2010 г. 240 с.
Если несколько лет назад кроме Цели на наших прилавках ничего не было, то сегодня книг по теории ограничений (ТОС) Голдратта не менее десяти. Ранее я уже представил вашему вниманию книгу Джеральда И. Кендалла «Действенное видение». В ближайшее время я обязательно расскажу и о других работах по ТОС, изданных на русском языке.
Скачать краткий конспект в формате Word2007 Голратт Я так и знал
Что привлекает читателей в теории Голдратта? На мой взгляд, это – эффективные и относительно простые решения, которые способны преобразовать компании в различных сферах деятельности. Это и производство, и дистрибуция, и розничная торговля. Сам Голдратт пишет в стиле бизнес-романов, а вот его последователи используют классическое научное строгое изложение. Поэтому, если представляемая книга является для вас первым знакомством с ТОС, то вы упустите, так сказать, подводную часть айсберга. Не переживайте! Во-первых, кое о чем скажу ниже. Во-вторых, можете почитать упоминавшегося выше Кенделла.В-третьих, и надводная часть очень даже полезна! J Годратт предлагает настолько очевидные решения, что после знакомства с ними возникает вопрос: «как же я не додумался до них сам!?»
Итак, в чем суть инновационного решения ТОС для розничной торговли?
- Непосредственно в магазинах следует хранить такое количество запасов, которое достаточно для обеспечения продажи от одного до нескольких дней.
- Пополнять запасы магазина следует с регионального склада малыми партиями ежедневно; если требуется, то даже поштучно! При этом надо ориентироваться на реальные результаты продаж.
- Запасы регионального склада следует пополнять с центрального склада относительно малыми партиями также ежедневно; при этом номенклатура пополнения может быть широкой; пополнять следует только те позиции, запас которых снизился ниже установленной нормы; например, ниже среднего недельного уровня продаж по всему региону + страховой запас (на случай значительного отклонения уровня продаж от среднего).
- Заказывать товар у поставщиков следует часто малыми партиями; в случае изменения текущих продаж, оперативно менять объемы заказов по конкретным артикулам; для этого надо выстраивать долгосрочные отношения с поставщиками, а не «метаться» от одного поставщика к другому.
- Благодаря сокращению запасов в каждом магазине, можно увеличить ассортимент товаров, что положительно скажется на объеме продаж.
- Снижение запасов и рост продаж позволяют значительно увеличить ROI – возврат на инвестиции: ROI пропорционален прибыли и обратно пропорционален стоимости запасов.
Очень важный момент – стремление разместить больше всего запасов как можно дальше от конечного потребителя, как можно ближе к основанию цепочки поставок. Это связано с тем, что отклонение ежедневных продаж от средних (в процентном выражении) больше в отдельных магазинах, чем по региону, и уж тем более по всей сети. Это следует из законов статистики: если средние значения продаж по магазинам надо просто суммировать, чтобы найти средние продажи по региону:
Х среднее по региону = Х среднее по первому магазину + Х среднее по второму + … + Х среднее по n-му
то среднеквадратичное отклонение определяется по формуле:
Например, если у нас 10 магазинов продают в среднем в день по 10 одеял, при этом с вероятностью 99% они продают не более 30 одеял, то:
1) если располагать дневные запасы в магазинах, нам потребуется 10*10 (среднее для одного магазина умножить на число магазинов) + 20*10 (страховой запас умножить на число магазинов) = 300 одеял
2) если располагать запасы на региональном складе с возможностью
ежедневного пополнения запасов магазинов, нам потребуется 10*10 (среднее) +![]()
(число магазинов умножить на квадрат страхового запаса) = 163 одеяла!
Ситуация с поставками мелкими партиями выгодна и поставщику! Во-первых, он может формировать график производства, заранее зная сроки поставки партий и ориентировочный объем. Во-вторых, он сокращает объем оборотных средств: оплата за отгруженную продукцию поступает ритмично; нет потребности накапливать на складе готовую продукцию для формирования большой партии. Для того чтобы логистика малых партий не стала дороже, необходимо увеличить ассортимент, так чтобы суммарный объем поставки был экономически эффективен (например, равнялся объему контейнера).
* * *
Помимо основной идеи – решения ТОС для розничной торговли – Голдратт освещает еще два полезных метода:
1) преодоление сопротивления переменам;
2) решение ключевой (корневой) проблемы.
Сопротивление переменам включает в себя несколько «эшелонов обороны»:
- несогласие с определением проблемы
- «да… но» существуют препятствия на пути реализации (отсутствие ПО, финансирования, компетенций…)
- несогласие с направлением действий по осуществлению решения
- несогласие с тем, что предложенное решение поможет преодолеть проблему
- «да… но» возможны негативные последствия
Для преодоления сопротивления переменам инициатор должен заранее подготовить аргументы. Люди сопротивляются переменам не по своей природе, а из-за того, что не видят личной пользы от перемен и видят риски для себя. Люди рассматривают плюсы и минусы как самих перемен, так и сохранения статус-кво, взвешивая риски, связанные с каждой из четырех составляющих. Только тогда они решают, принять изменения или нет. Покажите пользу и уменьшите риски! Склонить людей к переменам не так уж и сложно. Если, конечно, они им и в самом деле выгодны!
А начать следует с согласования ключевой проблемы и демонстрации путей ее решения. Голдратт использует метод (диаграмму) «Грозовая туча». Вот как она выглядит в случае розничной торговли:
Читают диаграмму следующим образом: «Для того чтобы быть успешным розничным продавцом, нужно много продавать и эффективно управлять запасами. Для того чтобы много продавать, нужно иметь значительные запасы. Для того чтобы эффективно управлять запасами, их объем нужно сокращать. Итак, чтобы быть успешным розничным продавцом нужно, с одной стороны увеличивать запасы, а с другой – сокращать. Имеется противоречие».
Диаграмма «грозовая туча» рисуется для ключевой проблемы. Для разрешения противоречия (для разгона тучи :)) необходимо «атаковать» связи 1 и 2. То есть, нужно показать, что одно из этих логических построений неверно:
1) Для того чтобы много продавать надо иметь большие запасы
2) Для того чтобы не «вылететь в трубу» надо иметь низкий уровень запасов
Какое логическое построение более сомнительно? Какое из них мы будем опровергать? Первое! Для того чтобы много продавать совсем не обязательно иметь высокий уровень запасов. Достаточно при малом уровне запасов часто их пополнять!
Если вам понравилась «туча», и вы хотели бы ее использовать в своей работе, предлагаю вам Шаблон Туча
[1] Сколько «т» писать в фамилии автора ТОС, вопрос тонкий… 🙂 Удвоение согласных в русском написании – «калька» с английского, где удвоение используется для превращения открытого слога в закрытый… По крайней мере, на сайте школы Голдратта используется написание с двумя «т».



Добрый день!
Что-то не совсем понятно с средним квадратичным отклонением: почему у Вас под корнем сумма дисперсий? по идее же надо брать сумму среднеквадратичных отклонений. Или я чего-то не понимаю? Просто тогда не очень понятен эк.смысл расчета. Поясните, пожалуйста!
Спасибо!
Максим, если х и у независимы, то дисперсия их суммы равна сумме их дисперсий. Именно дисперсий. См., например,
правило D5. Поэтому под знаком корня с складываю дисперсии. А чтобы найти суммарное скреднеквадратичное отклонение извлекаю квадратный корень.Спасибо за ответ! Я имел ввиду вот что: корень квадратный из 4 + корень квадратный из 4 будет равно 4. Так ведь? А вот корень квадратный из 4+4 (из 8) не будет равен 4. Поэтому я и спрашиваю, зачем под корень добавлять сумму дисперсий, когда надо бы искать сркв откл как корень квадратный из каждой дисперсии?
Максим, еще раз. У нас есть несколько случайных величин. Среднее значение суммы этих случайных величин равно сумме средних значений. Дисперсия суммы случайных величин равна сумме дисперсий каждой из них. А вот утверждение «среднеквадратичное отклонение суммы случайных величин равно сумме среднеквадратичных отклонений каждой из них» неверно.
Вас понял, видимо я где-то чего-то не понимаю. Вполне допускаю это. Однако, чисто по логике, какова дисперсия по 2 магазинам из примера? Я правильно задал вопрос? Спасибо!
Дисперсию принято обозначать символом «сигма в квадрате». Ответ на ваш вопрос:
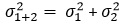
Доброе утро! Идея, описанная у Голдратта, очень интересна, но у меня появились сомнения. И вот почему. Дисперсия, как я думал равна Ơ²=Σn(x¡-x¯)²/n, где ¡ от 1 до n. Тогда дисперсия второго магазина будет равна ((30-10)^2 + (30-10)^2)/2 = 400. Дисперсия первого магазина — также равна 400. Тут-то у меня и возникает вопрос: среднеквадратичное отклонение по двум магазинам не будет ли равно сумме среднеквадратичных отклонений по каждому магазину? То есть Ơ = √Ơ1²+√Ơ2², а не √Ơ1²+Ơ2². Вот в чем был мой вопрос. Потому что «корень квадратный из 4 + корень квадратный из 4 будет равно 4…. А вот корень квадратный из 4+4 (из 8) не будет равен 4». Или я слишком смело трактую математические соотношения? Спасибо!
Но математически все верно же… А цифры разные получаются!
Ладно, видимо я разобрался. не судите строго! Мы же находим сигму по региону, а не по каждому магазину. А Вы где преподаете, если не секрет? Спасибо!