В рамках подготовки курса для бакалавров МФТИ я понял, что в моем блоге не так много заметок по использованию Excel в математике и физике. Каково же было мое удивление, что книг по теме на русском языке буквально единицы. Поэтому я не оставил без внимания даже издание 1999 г.!
В конспекте я не стал упоминать общие принципы работы в Excel, а сконцентрировался на предметной области: ряд Тейлора, функция Бесселя, Гамма-функция, интегрирование по правилу прямоугольников, решение нелинейных алгебраических уравнений методом последовательных приближений, решение систем линейных уравнений матричным методом, решение обыкновенных дифференциальных уравнений: задачи Коши методом рядов Тейлора, решение гиперболических дифференциальных уравнений в частных производных.
Вильям Дж. Орвис. Excel для ученых, инженеров и студентов. – Киев: Юниор, 1999. – 528 с.

Скачать краткое содержание в формате Word или pdf, примеры в формате Excel (конспект составляет около 4% от объема книги)
Глава 7. Суммирование радов
Многие функции, используемые в научных и инженерных расчетах, представляются только в виде рядов. В особенности это касается дифференциальных уравнений — их решения зачастую невозможно представить в виде замкнутого выражения, только в виде ряда. Примерами рядов, являющихся решениями дифференциальных уравнений, могут служить функции Бесселя, полиномы Лежандра и Лагерра.
Сумму ряда в Excel можно вычислить тремя способами:
- вычислить значение каждого члена ряда и затем сложить эти значения,
- создать итерационную формулу, вычисляющую за один проход значение одного слагаемого и добавляющую его к решению,
- написать функцию на VBA.
Суммирование членов рядов
Простейшим способом вычисления суммы ряда является расположение всех членов в соседних ячейках и их суммирование. Такой способ является наиболее понятным, поскольку позволяет увидеть, как происходит суммирование, и оценить сходимость ряда.
Встроенная функция Excel РЯД.СУММ может суммировать только степенные ряды следующего вида:
![]()
Все аргументы являются обязательными. Здесь x – значение переменной степенного ряда, n – показатель степени x для первого члена степенного ряда, m – шаг, на который увеличивается показатель степени n для каждого следующего члена степенного ряда, коэффициенты: а1, a2, a3, …, aj – набор коэффициентов при соответствующих степенях x. Количеством значений в аргументе коэффициенты определяет количество членов степенного ряда. Например, если в аргументе коэффициенты три значения, то степенной ряд содержит три слагаемых.
Известно, что синус можно приблизительно вычислить с помощью ряда Тейлора[1]
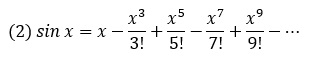
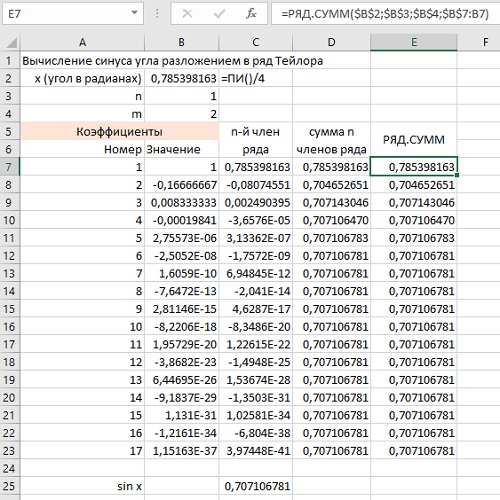
Рис. 1. Вычисление sin(π/4) различными методами (формулы см. в файле Excel)
Для большинства рядов, используемых на практике, обычно существуют рекуррентные соотношения, связывающие между собой последовательные члены ряда. Зачастую такая связь состоит в существовании специального сомножителя, произведение которого с любым членом ряда дает следующий член. Использование рекуррентных соотношений упрощает вычисления. Покажем работу рекуррентной формулы на примере функции Бесселя.
Функции Бесселя
Функции Бесселя Jn(x) являются решением дифференциального уравнения Бесселя:
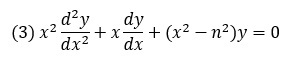
при у = Jn(x).
Это уравнение встречается во многих физических задачах, например, при решении волнового уравнения в цилиндрических координатах. Хотя функции Бесселя определены для произвольных значений n, чаще всего встречаются функции целого порядка. Для целых значений n функция Бесселя представляется в виде ряда:
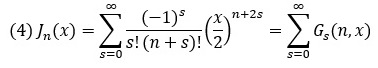
Для нахождения величин Gs(n,x), являющихся членами ряда для функции Бесселя целого порядка, можно воспользоваться рекуррентным соотношением:
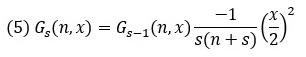
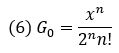
При использовании рекуррентных соотношений факториал вычисляется только один раз для первого слагаемого (G0). Остальные члены ряда получаются путем умножения предыдущего члена на рекуррентный множитель.
В следующем примере вычисляются значения функции Бесселя целого порядка n. Суммирования первых десяти членов ряда оказывается достаточным для получения ошибки менее одного процента для значений x, не превышающих восьми. Кроме того, в Excel имеется встроенная функция Бессель.J. Она используется для проверки точности вычислений членов ряда. равных 7,8. Если нужно провести вычисления для больших значений x или увеличить точность текущих значений, необходимо увеличить число слагаемых.

Рис. 2. Нахождение функции Бесселя различными методами
Используя данный метод, можно вычислять функцию Бесселя для целого набора значений х:
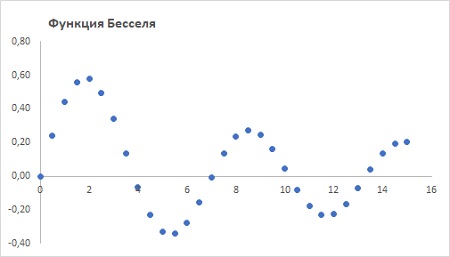
Рис. 3. Функция Бесселя для нескольких значений х
Метод итераций
Вторым способом вычисления рядов является использование итерационных возможностей Excel. Формула в рабочем листе создается таким образом, что при каждом вычислении определяется следующий член ряда и прибавляется к накопленной сумме. Для этого необходимо отключить автоматический пересчет листа и включить режим итераций. Также необходимо научиться запускать подсчет суммы, начиная с нулевого члена.
В качестве примера вновь рассмотрим задачу нахождения функции Бесселя. Создайте лист:
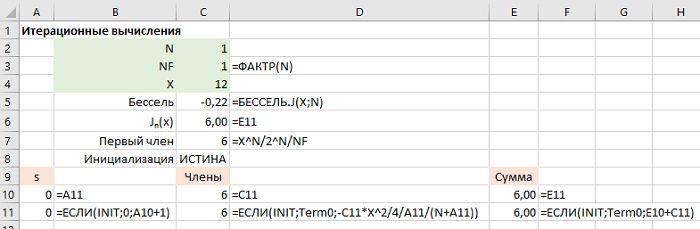
Рис. 4. Расчет функции Бесселя итерационным методом
Формулы показаны справа от ячеек. Поименованные ячейки выделен салатным цветом. Пройдите по меню Файл –> Параметры. В окне Параметры Excel перейдите на закладку Формулы и настройте Параметры вычислений как показано ниже:
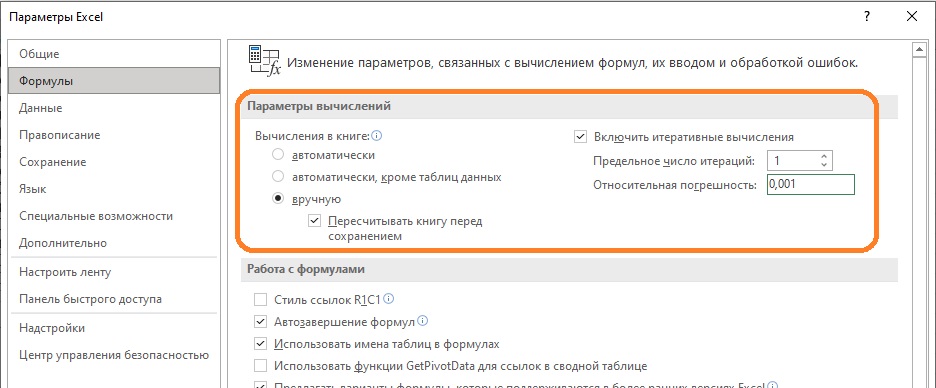
Рис. 5. Настройка итерационных вычислений; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Для использования этого листа необходимо ввести значения х и n и нажать клавишу <F9> для пересчета формул листа. Затем изменить значение ячейки С8 на ЛОЖЬ и нажать <F9> несколько раз. Номер члена отображается в ячейке А10, значение следующего члена, который будет прибавляться, — в ячейке С11 и текущее значение суммы ряда отображается в ячейках Е11 и С6. Ниже показан результат вычислений после 16 итераций для х = 12 и n = 1.
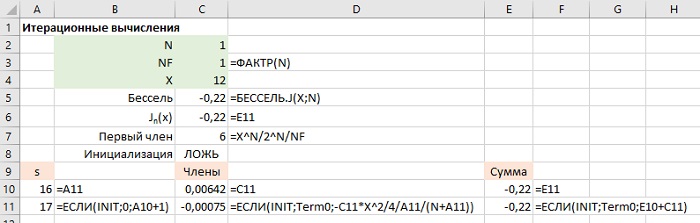
Рис. 6. Значение функции Бесселя для х = 12 и n = 1 после 16 итераций
Работа листа основана на трех циклических ссылках: между ячейками А10 и А11, С10 и С11 и Е10 и Е11. Формулы в ячейках А10, С10 и Е10 хранят текущие значения, в то время как формулы в ячейках А11, С11 и Е11 используют эти текущие значения для вычисления следующих номера итерации, члена ряда и суммы рядя. Функция ЕСЛИ в ячейках А11, С11 и Е11 запускают вычисление с нулевого члена в случае, если значение INIT (С8) равно ИСТИНА.
Для вычисления значения функции Бесселя при других значения параметров, необходимо ввести новые значения х и n, заменить С8 на ИСТИНА, нажать на клавишу <F9>, заменить значение С8 на ЛОЖЬ и нажимать на <F9> до тех пор, пока ряд не сойдется.
Увеличив значение поля Предельное число итераций (см. рис. 5), можно выполнять несколько итераций после одного нажатия на клавишу <F9>. Вычисления будут производиться или указанное число раз или пока изменения всех величин рабочего листа не станут меньше значения, указанного в поле Относительная погрешность. Будьте внимательны! После окончания подобных вычислений верните настройки Параметров вычисления в первоначальное состояние. Эти настройки относятся не к книге, а к приложению Excel. После этого Excel предупредит, что на листе содержатся циклические ссылки.
Глава 8. Интегрирование и дифференцирование
Интегрирование дискретных данных включает в себя аппроксимацию этих данных известной функцией с последующим ее интегрированием. В большинстве случаев не удается подобрать одну функцию для аппроксимации на всем интервале, поэтому область интегрирования разделяется на большое количество подынтервалов, на каждом из которых используется простая функция типа линейной, квадратической или кубической. После чего результаты для отдельных подынтервалов складываются вместе для получения полного интеграла.
Наиболее часто при численном интегрировании используются правило прямоугольников, правило трапеций, интегрирование по Ромбергу, правило Симпсона и квадратура Гаусса. Каждый из этих методов является более точным, чем предыдущий, поскольку производит аппроксимацию данных более сложной кривой.
Правило прямоугольников
Согласно правилу прямоугольников, область между точками заполняется прямоугольником, высота которого соответствует координате у одной из точек, а ширина равна расстоянию между точками. Значение интеграла определяется формулой:
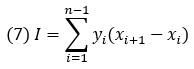
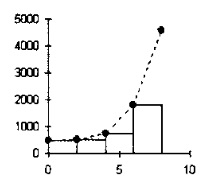
Рис. 7. Интегрирование по правилу прямоугольников
Такое приближение может показаться очень грубым, например для случая, указанного на рисунке, однако при малой ширине интервала и гладкой функции результаты получаются достаточно точными. Кроме того, такой метод очень просто реализовать, поскольку достаточно просто перемножить данные в каждой точке на ширину интервала и сложить результат.
Чтобы воспользоваться одним из методов интегрирования, в ячейках Excel вычислите значения интеграла между двумя точками. В последней ячейке все эти значения суммируйте.
Гамма-функция
Гамма-функция – специальная функция науки и техники. Она появляется в физических задачах, например, при вычислении вероятностей в статистической механике или при нормировке волновых функций в кулоновском поле. Гамма-функция может использоваться в виде сомножителя в выражении для функции Бесселя Jn(x) в случае нецелого значения n. При целых значениях аргумента гамма-функция становится обычным факториалом.
(8) Г(n + 1) = n!
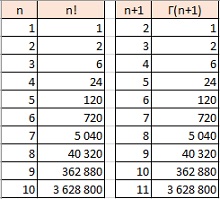
Рис. 8. Гамма-функция и факториал в Excel
Гамма-функция определяется следующим интегралом…
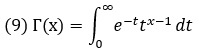
…не имеющим аналитического выражения. Значения гамма-функции обычно задаются таблично или находятся в Excel с помощью функции ГАММА(). Ниже приведен график подынтегральной функции для х = 1,5. Обратите внимание, что выражение быстро стремится к нулю, поэтому интеграл можно оборвать при t = 10.
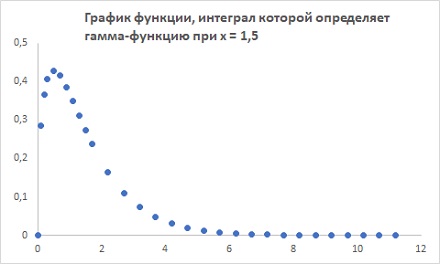
Рис. 9. График функции, интеграл которой определяет гамма-функцию при х = 1,5
Вычислим гамма-функцию с помощью численного интегрирования методом прямоугольников. Точное значение гамма-функции в точке х = 1,5 в Excel задается формулой =ГАММА(1,5). Используем это значение, как эталон для наших вычислений. Поименованные переменные выделены салатным цветом. В ячейках А11 и В11 формулы используют функции динамических массивов (доступны в Excel 365). В диапазоне D10:E26 расположена Таблица данных. Если вы ранее не сталкивались с этим инструментом Excel, рекомендую посмотреть здесь. Вы можете поиграть со значением TMAX. Выше упоминалось, что интеграл можно оборвать при t = 10, так вот, этого недостаточно. Значение, не отличающееся от эталонного в пятом знаке после запятой, можно получить при TMAX = 20.
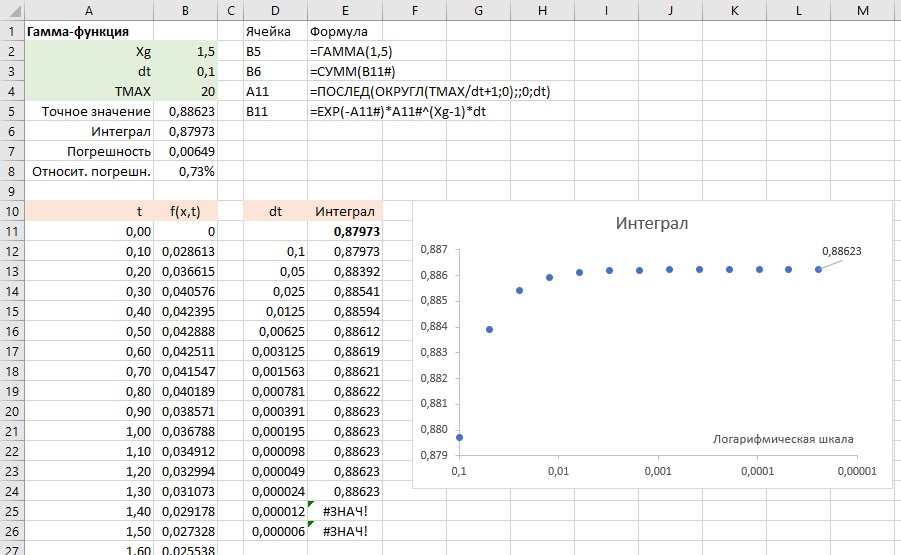
Рис. 10. Значение интеграла, полученное методом прямоугольников
Глава 9. Решение нелинейных алгебраических уравнений
Большинство нелинейных алгебраических уравнений не допускает аналитического решения. Численные методы решения нелинейных уравнений основаны на угадывании начального приближения к решению и последовательном улучшении этой догадки. Очередное приближение вносится в уравнение, а результат используется для построения следующего приближения. Эта процедура повторяется до тех пор, пока не будет достигнута удовлетворительная точность приближенного решения. Итерационный процесс может оказаться расходящимся…
Хотя для нахождения корней нелинейных уравнений существует целый ряд методов, лучше всего для реализации в Excel подходит метод последовательных приближений. Для его применения уравнение необходимо переписать в виде:
(10) x = f(x)
Записать уравнение в таком виде можно несколькими способами. Из них нужно выбрать тот способ, который приводит к сходимости. Далее необходимо выбрать начальное значение х — первое приближение к решению. В принципе может подойти любое значение, но чем ближе оно к точному решению, тем быстрее к нему сойдется итерационный процесс. Если уравнение имеет несколько решений, различные начальные приближения могут привести к различным корням.
Подставьте начальное значение х в функцию f(х) и вычислите новое значение х. Это значение будет являться вторым приближением, которое снова подставляется в f(х). Продолжайте вычисление новых приближений х до тех пор, пока последовательность не сойдется к пределу с удовлетворительной точностью.
Ниже показана последовательность приближений к решению нелинейного уравнения. График иллюстрирует поиск решения уравнения х = cos(x), которое находится в точке пересечения кривых у = х и х = cos(x). Итерационный процесс напоминает приближение к решению по сужающейся спирали; вычисления прекращаются тогда, когда очередное приближенное значение оказывается достаточно близким к точному решению.
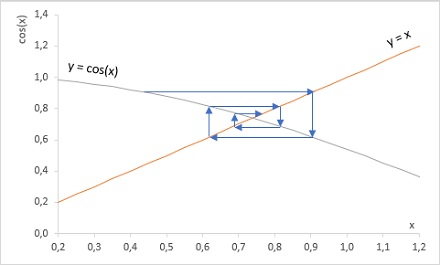
Рис. 11. Последовательные приближения к решению нелинейного уравнения
Решим это уравнение с использованием итераций в Excel. Для реализации метода отключите автоматический пересчет листа и введите формулы с рекурсией (циклическими ссылками).
Как правило, ячейки листа пересчитываются в нормальном порядке. Это означает, что аргументы ячейки (то есть те ячейки, от которых зависит ее значение) вычисляются до того, как пересчитывается значение самой ячейки. Это правило применяется ко всем ячейкам листа, пока все они не будут пересчитаны. При изменении значения ячейки пересчитываются все ячейки, значения которых зависят от нее прямо или косвенно. Рекурсия, или циклическая ссылка, имеет место в том случае, когда значение ячейки зависит от нее самой, как прямо, так и косвенно через значения других ячеек. В нормальном порядке такое значение вычислить нельзя, поскольку нельзя определить аргументы ячейки, в число которых входит она сама — получается, что для определения значения ячейки необходимо сразу знать его заранее!
В итерационном режиме вначале пересчитываются только те ячейки листа, которые не содержат циклических ссылок. Затем ячейки, содержащие циклические ссылки, итерируются один или несколько раз, в зависимости от значения, установленного в окне Параметры Excel (см. рис. 5). Ячейки, содержащие циклические ссылки, вычисляются с текущими значениями аргументов без их предварительного пересчета. Пересчет прекращается после выполнения указанного в окне количества итераций. Чтобы заново пересчитать все ячейки, щелкните на кнопке Вычислить или нажмите <F9>. Этот способ используется для последовательного вычисления значения по заданной формуле и подстановки его в ту же формулу.
Установим количество итераций равным 1, чтобы наблюдать за изменением значений при пересчете листа. На практике для более быстрого нахождения решения лучше выбрать большее количество итераций. Создайте таблицу с начальным значением и флагом инициализации. Флаг инициализации переводит лист в заданное начальное состояние.
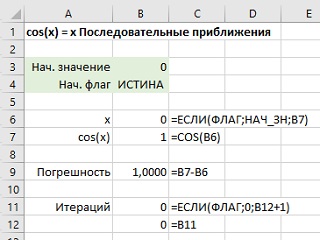
Рис. 12. Применение метода последовательных приближений для решения уравнения cos(x) = х
Присвойте ячейке В3 имя НАЧ_ЗН и введите в нее 0, а ячейке В4 имя ФЛАГ и введите значение ИСТИНА. В ячейке В6 будет выполняться проверка ФЛАГ = ИСТИНА. Если это так, х будет установлено равным НАЧ_ЗН, в противном случае — равным ячейке В7, т.е. cos(х). В ячейке В7 вычисляется косинус ячейки В6, и тем самым организуется циклическая ссылка. Далее следует вычислить погрешность — разницу между х и cos(x) — которая будет служить критерием сходимости процесса последовательных приближений.
Теперь в ячейках В11:В12 организуйте вторую циклическую ссылку — для подсчета количества итераций.
Для начала расчетов установите значение флага в ячейке В4 равным ИСТИНА, и нажмите <F9> для запуска решения задачи. Измените значение начального флага на ЛОЖЬ и снова нажмите <F9>. При каждом нажатии <F9> выполняется одна итерация и вычисляется следующее приближенное значение х. Нажимайте <F9> до тех пор, пока значение х не достигнет необходимой точности.
Точность полученного приближенного значения х проверяется путем его сравнения со значением cos(х); разность между ними отображается в ячейке В9. После 25 итераций погрешность стала менее 0,0001.
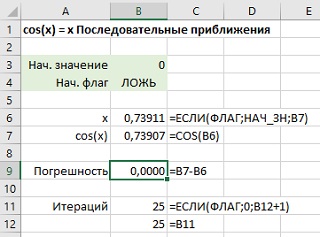
Рис. 13. После 25 итераций погрешность стала меньше 0,0001
Отслеживание значений х и прекращение вычислений после достижения нужной точности может выполняться в Excel автоматически. В окне Параметры Excel (см. рис. 5) установите Предельное число итераций = 100, Относительная погрешность = 0,001, в области Вычисления в книге установите Автоматически. Инициализируйте вычисления путем ввода значения ИСТИНА в ячейку В4. Значения пересчитаются автоматически. Запустите процесс последовательных приближений путем ввода в ячейку В4 значения ЛОЖЬ.
Если процесс сходится медленно, предельное количество итераций (100), будет достигнуто раньше, чем заданная точность. В этом случае нажмите клавишу <F9> для выполнения еще ста итераций. Повторяйте эту процедуру столько раз, сколько необходимо.
Глава 10. Решение систем уравнений
Многие встречающиеся на практике вычислительные задачи сводятся к решению систем линейных уравнений. Они могут быть решены с помощью встроенных матричных функций Excel, поддерживающих обращение и умножение матриц.
Физические задачи сводятся к системам линейных уравнений, как правило, не благодаря какому-нибудь общему физическому закону, а ввиду упрощения математических моделей реальных процессов. При замене исследуемой физической системы ее математический моделью область определения решения разбивается на достаточно мелкие фрагменты, внутри каждого из которых функции, описывающие поведение системы, аппроксимируются линейными функциями. В результате получается система линейных уравнений, соответствующих каждому из фрагментов области.
Матричные методы
Для их применения систему необходимо записать в матричной форме:
(11) Ax = b
Здесь А — матрица коэффициентов, х — вектор неизвестных, а b — вектор правой части уравнений. Для решения этого матричного уравнения обе его части умножаются на матрицу, обратную к А:
(12) A-1Ax = A-1b
По определению, произведение матрицы на обратную к ней дает единичную матрицу, а произведение единичной матрицы на любой вектор равно этому же вектору, поэтому предыдущее уравнение преобразуется к следующему виду:
(13) x = A-1b
Это и есть решение системы уравнений. Хотя в абстрактном виде все выглядит очень просто, нахождение обратной матрицы — задача достаточно нетривиальная. К счастью, в Excel есть функция МОБР().
Краткая справка по матричной алгебре
Вкратце напомним основные правила матричной алгебры — действия с числовыми матрицами и векторами. Чтобы умножить одну квадратную матрицу на другую, для вычисления каждого элемента результата с индексами (m,n) берется m-я строка из левой матрицы и n-й столбец из правой, все элементы строки умножаются на соответствующие по порядку элементы столбца, и результаты умножения складываются:
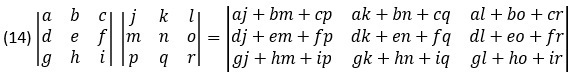
Произведение матрицы на вектор — это произведение квадратной или прямоугольной матрицы на матрицу, состоящую из одного столбца:
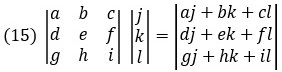
Матрица, обратная к данной матрице — это, по определению, матрица, в результате умножения которой на данную получается единичная матрица, то есть такая квадратная матрица, на диагонали которой стоят единицы, а на всех остальных местах — нули:
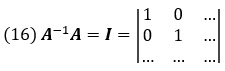
Умножение единичной матрицы на любую матрицу или вектор дает в результате ту же матрицу или вектор, что аналогично умножению любого числа на единицу:
(16а) Ix = x
Матрица называется вырожденной, если какая-либо из ее строк является линейной комбинацией других строк. Вырожденная матрица не содержит достаточной информации для решения соответствующей линейной системы. Матрица вырождена тогда и только тогда, когда ее определитель равен нулю.
Система из трех уравнений с тремя неизвестными
В качестве примера рассмотрим следующую систему линейных уравнений:
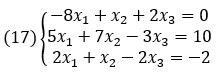
В матричной форме эти уравнения записываются следующим образом:
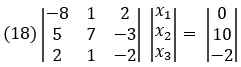
Такую систему можно решить в Excel с использованием двух функций массива: МОБР() и МУМНОЖ().
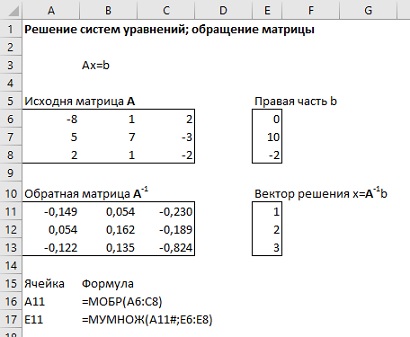
Рис. 14. Решение системы линейных уравнений с помощью матричных функций
Глава 11. Решение обыкновенных дифференциальных уравнений
Благодаря динамической связи ячеек и итерационным возможностям в Excel можно решать самые разные дифференциальные уравнения. Численному решению поддаются два основных типа задач для обыкновенных дифференциальных уравнений: задачи Коши (или начальные задачи) и краевые задачи. Отличие между этими двумя типами задач состоит не в типе рассматриваемых дифференциальных уравнений, а в локализации граничных условий.
Решение задач Коши
В задачах Коши, или начальных задачах, для однозначного определения решения дифференциального уравнения на одном из концов рассматриваемой области определения решения задают начальные (граничные) условия. Целью приближенного решения является интегрирование уравнения от конца с известными граничными условиями до другого конца интервала, на котором они неизвестны. Такого типа задачи обычно возникают для уравнений с производными по времени: известно значение искомой функции и некоторых ее производных в данный момент времени (определенная граница), и требуется найти ее значения для всех или некоторых моментов в будущем (на неизвестной границе).
Рассмотрим следующее обыкновенное дифференциальное уравнение первого порядка:
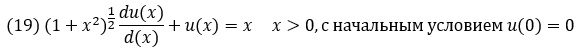
Это задача Коши, поскольку граничное условие известно только в одной точке. Задачи для уравнений первого порядка не должны содержать более одного дополнительного условия, так как в противном случае задача оказалась бы переопределенной и, скорее всего неразрешимой. Для уравнений второго и более высокого порядка необходимо задавать большее количество начальных или граничных условий.
Для понимания того, зачем для решения дифференциальных уравнений необходимо задавать одно или несколько граничных условий, рассмотрим следующее функциональное уравнение:
(20) y=f(x)
Имея это уравнение, можно начертить график значений у для всех требуемых значений независимой переменной х. Это уравнение полностью определено, и для однозначного определения значений у не требуется присоединять к нему дополнительные условия. Теперь рассмотрим другое уравнение:
(21) y’=f(x)
Это уравнение является дифференциальным и имеет первый порядок, определяя для каждого х значение производной функции y’. Производная описывает тангенс угла наклона касательной к графику функции; зная ее, можно начертить форму кривой, однако нельзя сказать, где именно кривая расположена. Все кривые на приведенном ниже рисунке удовлетворяют этому уравнению — поэтому для выбора решения необходимо знать значение функции хотя бы в одной точке, например, в черной точке на левом краю рисунка. Значение функции в этой точке и будет представлять собой граничное условие.
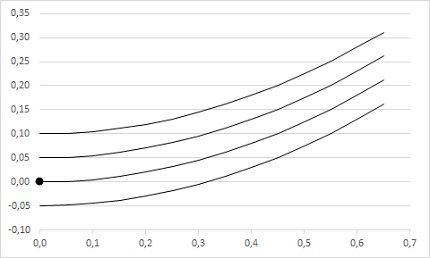
Рис. 15. Для выбора конкретной кривой из семейства требуется задать значение функции в точке х = 0
Далее рассмотрим вторую производную функции:
(22) y’’=f(x)
Из этого уравнения нам известна кривизна графика функции для каждого значения х. Определить по ней всю недостающую информацию о функции можно только в том случае, если в одной точке заданы значение функции и ее производной (начальная задача) или значения функции в двух точках (краевая задача). Эти условия и будут краевыми условиями для данной задачи. Итак, для получения однозначного решения дифференциального уравнения необходимо присоединить к нему столько граничных условий, каков порядок уравнения. Если в уравнение входит более одной независимой переменной (например, две для плоских задач математической физики), граничные условия должны задаваться на границах изменения каждой из переменных.
Наша цель – найти значения функции u(x), являющейся решением уравнения (19), для х от 0 до 0,2. Для уравнения (19) известно аналитическое решение:
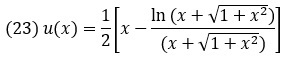
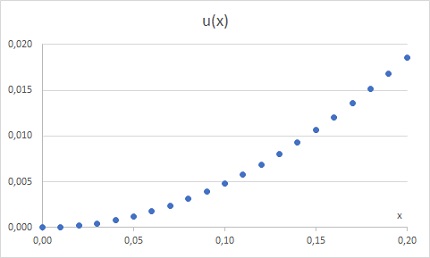
Рис. 16. Функция аналитического решения в диапазоне от 0 до 0,2
Эту функцию будем использовать для оценки эффективности приближенного метода.
Метод рядов Тейлора
Одним из распространенных методов решения начальных задач является метод рядов Тейлора. Рассмотрим разложение некоторой функции u(х) в ряд Тейлора в окрестности точки х0.
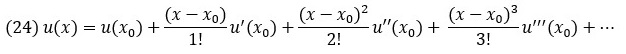
где
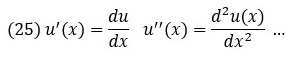
Положим h = (х – x0). Уравнение (24) примет вид:
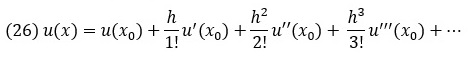
В точке x0 известны значения двух первых членов ряда Тейлора: первый — из граничного условия, а второй — из дифференциального уравнения: u(0) = 0, u’(0) = 0. Последовательно дифференцируя уравнение, которое представляет собой выражение для первой производной, получаем выражения для производных более высокого порядка. Из этих выражений получаем следующие коэффициенты: u’’(0) = 1, u’’’(0) = –1, u’’’’(0) = –2.
Подставим эти коэффициенты в первые пять членов ряда Тейлора и отбросим остальные члены ряда. Усечение ряда Тейлора допустимо только в том случае, если отброшенные члены в сумме достаточно малы, что в свою очередь справедливо только при малых h. Получим для решения следующее приближение:
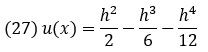
Это решение может использоваться для вычисления значений искомой функции для различных h. Вычислим значения u(х) для от 0 до 0,2.
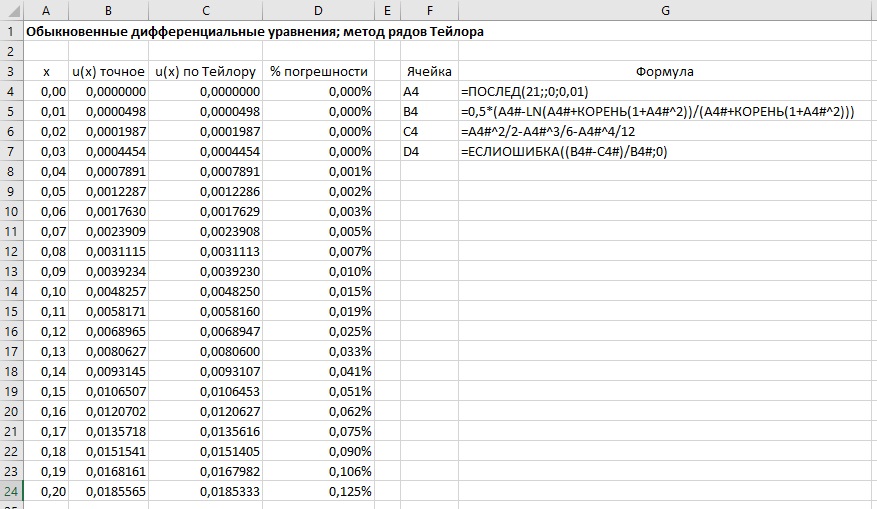
Рис. 17. Решение задачи Коши методом рядов Тейлора
Обратите внимание, что для малых значений х приближенное решение является точным. С ростом х погрешность возрастет. Следует обратить внимание, что в примере h — это расстояние от х до х0, а не шаг численного интегрирования. Для вычисления значений u на больших расстояниях от х0 необходимо пересчитывать значения производных в конце текущего шага, чтобы выполнить следующий шаг уже от этой точки.
Глава 12. Решение дифференциальных уравнений в частных производных
Дифференциальные уравнения в частных производных – наиболее распространенный аппарат математического моделирования физических процессов. Во многих случаях по причине независимости пространственных и временных координат вместо обыкновенных дифференциальных уравнений используются уравнения в частных производных. Как и обыкновенные дифференциальные уравнения, уравнения в частных производных обычно не имеют аналитических решений, или же эти решения очень трудно отыскать. Поэтому, как и в случае обыкновенных дифференциальных уравнений, для решения уравнений в частных производных чаще всего применяются численные методы.
Для дважды непрерывно дифференцируемой функции u, зависящей от двух независимых переменных х, у, можно записать пять различных частных производных:
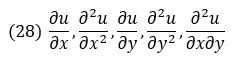
Из них можно составить следующее общее линейное уравнение в частных производных:
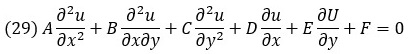
Каждый из коэффициентов A–F также может представлять собой функцию двух независимых переменных х, у.
Различие между обыкновенными дифференциальными уравнениями и уравнениями в частных производных состоит отнюдь не в употреблении символов d или ∂ для обозначения производных. В обыкновенное дифференциальное уравнение входит одна независимая переменная, функции этой переменной и производные функций по ней же. Так, следующее уравнение содержит независимую переменную х, функции этой переменной u(х) и Зх, а также первую и вторую производные неизвестной функции по независимой переменной. Оно является обыкновенным, несмотря на символ частной производной:
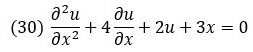
В дифференциальное уравнение в частных производных входит две или более независимые переменные, функции этих переменных и частные производные функций по этим переменным. Например, следующее уравнение содержит две независимые переменные (х и у), функции независимых переменных (u(х, у) и Зх+5у), а также частные производные по одной или обеим независимым переменным:
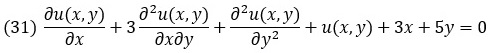
Классификация типов уравнений в частных производных
Линейные дифференциальные уравнения в частных производных второго порядка подразделяются на три типа: эллиптические, параболические и гиперболические уравнения. Тип уравнения определяется соотношениями между коэффициентами при вторых производных искомой функции. Например, для уравнений с двумя независимыми переменными тип определяется следующими условиями на знак дискриминанта:
- эллиптический: B2 – 4AC < 0
- параболический: B2 – 4AC = 0
- гиперболический: B2 – 4AC > 0
Поскольку коэффициенты сами являются функциями независимых переменных, в разных точках области определения искомой функции уравнения могут иметь различный тип.
Решение гиперболических уравнений в частных производных
Поскольку дискриминант положителен, в уравнении присутствуют вторые производные по обеим переменным. Гиперболические уравнения возникают при исследовании механических колебаний и волн, процессов переноса (например, излучения), а также в задачах диффузии и газовой динамики. Наиболее важным для современной физики и техники является волновое уравнение. Оно используется, например, для моделирования электромагнитных волн в вакууме и электронных свойств твердых полупроводников. Это уравнение содержит вторые производные по пространственной координате и времени с коэффициентом пропорциональности между ними в виде квадрата скорости волны:
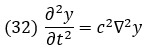
Здесь с — скорость бегущей волны. Волновым уравнением описывается как электромагнитная волна в пространстве, так и волна в колеблющейся струне. Рассмотрим одномерную форму этого уравнения:
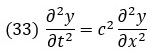
Вначале заменим производные центральными разностями:
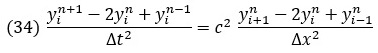
Теперь решим это уравнение относительно значения искомой функции в будущем времени:
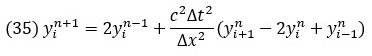
Для определения следующего значения функции необходимо знать ее значения на двух предыдущих шагах. Это представляет некоторую проблему только на первых двух шагах, когда у нас нет предыстории процесса, позволяющей определить значения . Для запуска итерационного процесса необходимо каким-то образом найти два недостающих значения. Если в качестве начальных значений заданы значение функции у и ее производной, то для определения значения функции в момент –∆t можно воспользоваться экстраполяционной формулой:
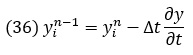
Для определения недостающего значения функции можно воспользоваться и другими видами начальных условий.
Колебания струны
Колебания тонкой упругой струны описываются одномерным волновым уравнением. Граничные условия заключаются в равенстве нулю перемещений закрепленных концов струны. Начальные условия определяются амплитудой и положением точки, в которой струну дергают в нулевой момент времени. Предположим, струна имеет длину 70 см и ее оттянули на 0,1 см в точке, отстоящей на 20 см от одного конца. В таком случае начальные условия будут иметь следующий вид:
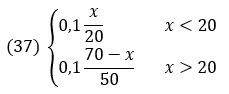
Для устойчивости разностной схемы коэффициент в разностном уравнении должен быть равен 1:
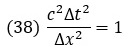
Замена этого коэффициента единицей также упрощает само разностное уравнение:
![]()
Сила натяжения струны определяет скорость бегущей в ней волны, которая в свою очередь задает соотношение между шагами по времени и по пространственной координате. Например, если растяжение струны задает скорость волны равной 5×104 см/с, шаги по времени и пространству будут соотноситься следующим образом:
![]()
Так, если шаг по пространственной координате ∆x составляет 10 см, то шаг по времени ∆t должен быть равен 2х10-4 с.
Из начальных условий известно, что в нулевой момент времени струну оттянули на некоторую величину, не придавая начальной скорости. Поэтому значение функции на первом шаге ∆t должно быть равно ее значению в момент –∆t:
![]()
Внесем это значение в разностное уравнение для первого шага:
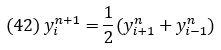
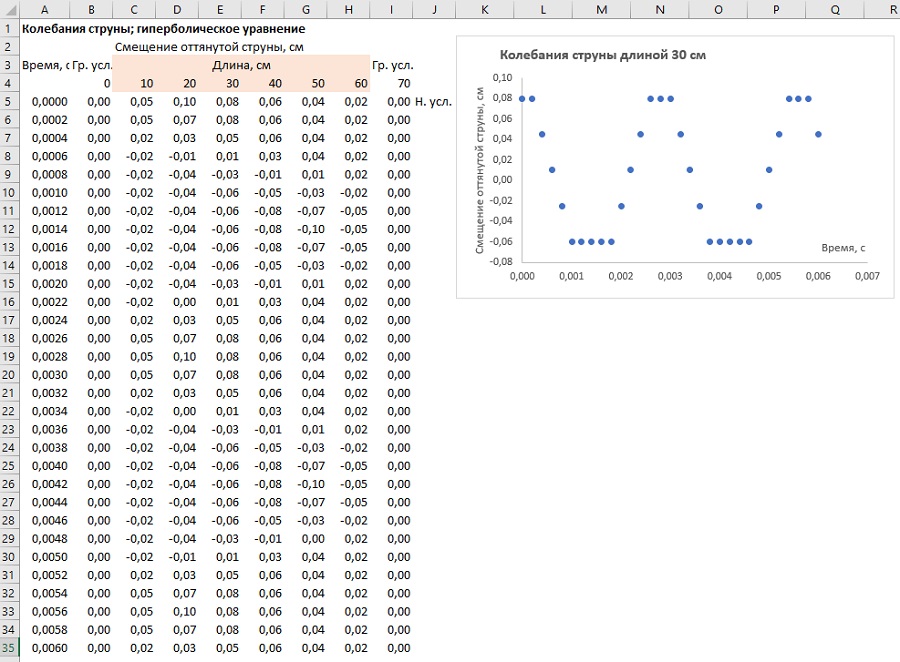
Рис. 18. Колебания струны: решение гиперболического уравнения в частных производных (формулы см. файл Excel)
Если проследить изменения в положении струны, можно заметить, что она колеблется с периодом 2.8×10-3 с, или частотой 357 Гц. Аналитическое выражение для частоты колебаний дает тот же результат:
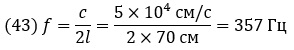
Здесь f – частота, а l — длина струны.
[1] При разложении функции в окрестностях точки х0 = 0 ряд Тейлора принято называть рядом Маклорена