Краткий конспект этой книги я подготовил еще в 2010 г. За это время качество моих конспектов выросло (я надеюсь :)), к тому же появился отличный повод перечитать книгу – Альпина выпустила второе издание (полностью идентичное первому). На самом деле, я считаю, что тема статистического управления недооценена в российском менеджменте. В то же время, она явилась одним из столпов японского чуда второй половины XX века. Лично на меня идеи Шухарта – Деминга оказали очень большое влияние. Это первая книга на русском языке, в которой ясно, наглядно и профессионально изложены принципы и методы статистического управления процессами на основе контрольных карт, разработанных Уолтером Шухартом в Bell Laboratories, и показаны недостатки традиционного подхода к контролю качества, основанного только на соблюдении допусков.
По теме см. также: У. Эдвардс Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами, Генри Р. Нив. Организация как система: Принципы построения устойчивого бизнеса Эдвардса Деминга.
Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. М.: Альпина Паблишер, 2016. – 410 с. (на английском языке книга впервые вышла в 1986 г.)
Скачать конспект (краткое содержание) в формате Word или pdf
Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon или Лабиринте
Предисловие к русскому изданию
Основная идея теории Шухарта очень проста: мир сложен, и точно предсказать результат большинства реальных процессов невозможно в принципе. Но для практики этого и не нужно: достаточно научиться предсказывать результаты с той степенью уверенности, которая экономически оправданна на данном этапе развития человечества и при данном уровне последствий принимаемых решений. Чтобы это сделать, следует принять во внимание, что большая часть результатов любого процесса определяется системой, в которой этот процесс проходит, и лишь небольшая их часть вызвана внешними по отношению к этой системе причинами.
Поэтому нам надо научиться определять, какие результаты принадлежат системе, а какие — внешним или внутренним внесистемным силам. Результатами, обусловленными системой, можно управлять, только изменяя саму систему. Но сначала надо устранить все внесистемные воздействия, поскольку они по определению неуправляемы и, следовательно, непредсказуемы. Инструментом, помогающим понять, какие воздействия принадлежат системе, а какие нет, и служат контрольные карты Шухарта (ККШ).
Что же такое особенное не разглядели статистики в работах Шухарта? Он обнаружил, что система, если она находится в стабильном, управляемом, устойчивом состоянии, ведет себя так, что ее результаты можно предсказывать с определенной точностью до тех пор, пока что-то или кто-то не выведет ее из этого состояния. Такую систему принято называть статистически управляемой. Предсказуемость позволяет управлять процессом, а значит, и улучшать его. Без предсказуемости никакое совершенствование невозможно.
Напротив, если есть какие-то внешние вмешательства в систему, то о предсказаниях можно забыть. Система становится не только непредсказуемой, но и неуправляемой. Тогда надо как можно быстрее выявить и устранить источник внешнего вмешательства и вернуть ее в управляемое состояние. Дело за малым. Нужно научиться различать состояния, в которых находится система, а затем решать, что и кому надо с ней делать (или не делать).
ККШ — это и есть диагностический инструмент для ответа на вопрос: надо или не надо вмешиваться в систему, и если надо, то кому? Он построен с помощью статистических методов, но сам не имеет статистической природы. Это сделано для того, чтобы модели могли избежать «смирительной рубашки» теоретической статистики. В условиях накопления информации система может и сама служить себе эмпирической моделью, гораздо более естественной, чем теоретические модели, навязанные извне. Их призвана заменить концепция операциональных определений.
За рассуждениями У. Шухарта скрывались не столько статистика, сколько экономика и его соображения о том, оправдаются ли расходы, связанные с выявлением признаков неуправляемости процесса, теми выгодами, которые мы получим благодаря их обнаружению и устранению.
Новый подход в середине прошлого века предложил Г. Тагути в Японии. Допуск остается рабочим инструментом проектировщика, конструктора и рабочего, но уходит из жизни продавца и потребителя. Ему на смену приходят индексы воспроизводимости. Они определяются соотношением между шириной поля допуска и естественной вариацией вашего процесса. Естественную вариацию процесса можно оценить. Обычно она выражается шестью квадратичными ошибками (плюс-минус три сигмы относительно среднего арифметического). Деление ширины поля допуска на шесть сигм как раз и дает величину индекса воспроизводимости Ср.
Но расчет и оценка индексов воспроизводимости возможны только для стабильных, т. е. управляемых процессов, а для этого надо вести ККШ — инструмент мониторинга и диагностики. Что же касается непрерывного совершенствования, то для него есть масса инструментов, которые в Японии объединены под «зонтиком кайдзен», а в США на той же основе разработана ныне весьма популярная методология «шести сигм». В рамках этой методологии ставится задача сжать естественную вариацию процесса настолько, чтобы она укладывалась в половину поля допуска.
Есть еще одна важная проблема, связанная с применением методов статистического управления процессами. Иногда кажется, что их внедрение чисто техническая задача. Сначала надо обучить людей, а затем предложить им использовать полученные знания на практике. При полной поддержке руководства. Но в действительности всякая работа с цифрами требует существенного изменения человеческих отношений в организации. Самое главное — категорически отказаться от идеи наказания и убедить сотрудников в искренности и необратимости такого отказа. Поскольку страх всегда порождает ложь, вы получите такие цифры, которые, как думают сотрудники, вы хотите получить.
Статистическое мышление — основа качества. Статистическое мышление — часть складывающейся на наших глазах более широкой концепции, призванной объединить время, деньги и вариабельность в новую парадигму менеджмента. Там-то статистическое мышление и развернется во всей красе.
Для кого предназначена эта книга? Прежде всего для менеджеров всех уровней, работающих в любых компаниях и организациях. Ведь, по сути, идея Шухарта-Деминга, если изложить ее простым языком, сводится к следующему: мы живем в мире, где результаты любого процесса подвержены вариабельности, т. е. случайным колебаниям. В таком мире нельзя принимать решения, основываясь на сравнении двух (трех, четырех) точек, вырванных из процесса. Надо обязательно смотреть на весь процесс в целом и отделять случайные колебания от возмущающих внешних воздействий.
Пока не стерты «случайные черты», нельзя даже говорить о разумных решениях. Если этого не делать, то мы обречены на то, что применительно к оценке людей называется наказанием невиновных и награждением непричастных. К сожалению, именно так принимаются сегодня многие управленческие решения. Большинство российских (и не только российских) менеджеров смотрит на любое отклонение от целевого значения как на проблему, требующую немедленного реагирования. А поскольку причина отклонения обычно неясна, то принимается простейшее решение, имитирующее активную реакцию, — наказание непосредственного исполнителя.
Ю. Адлер, В. Шпер
Литература
Адлер Ю.П., Шпер В.Л. Истоки статистического мышления // ММК, 2003, № 1, с. 34-40. (Это первая статья серии из восьми публикаций в журнале «Методы менеджмента качества», посвященных пониманию и применению ККШ. См. также: ММК, 2003, № 3, 5, 7, 11; 2004, № 2, 3, 6.)
Shewhart W. (1931, reprint 1980). Economic Control of Quality of Manufactured Product. — Milwaukee, WI: ASQ Quality Press. — P. 501.
Shewhart W.A. (1939, reprint 1986). Statistical Method from the Viewpoint of Quality Control. — N.Y., Dover Publications, Inc. — 163 р.
Деминг Э. Выход из кризиса: Новая парадигма управления людьми, процессами и системами: Пер. с англ. — М.: Альпина Бизнес Букс, 2007. — 370 с.
Деминг Э. Новая экономика: Пер. с англ. — М.: Эксмо, 2006. — 208 с.
Глудкин О.П., Горбунов Н.М., Гуров А.И. и др. Всеобщее управление качеством. — М.: Радио и связь, 1999. — 600 с.
Ильенкова С.Д. и др. Управление качеством. — М.: ЮНИТИ, 1998. — 199 с.
Жулинский С.Ф., Новиков Е.С., Поспелов В.Я. Статистические методы в современном менеджменте качества. — М.: Фонд «Новое тысячелетие», 2001. — 208 с.
Мердок Дж. Контрольные карты: Пер. с англ. — М.: Финансы и статистика, 1986.
Шиндовский Э., Шюрц О. Статистические методы управления качеством. Контрольные карты и планы контроля: Пер. с нем. — М.: Мир, 1976.
Миттаг Х.-Й., Ринне Х. Статистические методы обеспечения качества: Пер. с нем. — М.: Машиностроение, 1995. — 616 с.
ГОСТ Р 50779.42-99. Статистические методы. Контрольные карты Шухарта.
Кумэ Х. Статистические методы повышения качества: Пер. с англ. — М.: Финансы и статистика, 1990. — 302 с.
Wheeler D. Understanding variations. The Key to Managing Chaos. — SPC Press. — 168 p.
Wheeler D. Advanced Topics in Statistical Process Control. — SPC Press, 1995. — 470 р.
Глава 1. Два подхода к вариации
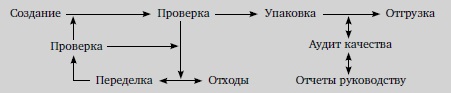
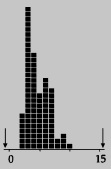
Суть инженерной концепции вариации состояла в попытке провести четкую линию между «хорошими» и «плохими» деталями (рис. 1). Однако, если производственный процесс производит практически однородную продукцию, то процесс выглядит иначе (рис. 2).
Рис. 1. Типичный западный производственный процесс
Рис. 2. Производственный процесс, при котором выпускается практически однородная продукция
Эта идея знаменует собой новый подход в менеджменте и производстве. Изучение максимально возможного числа источников вариации, влияющих на качество конечного продукта, а также принятие мер по ее снижению должны стать ежедневными задачами менеджеров. Пока это не так, устаревший метод сортировки, переделки и повторной сортировки будет гарантированно приводить к отсутствию прогресса, низкой производительности и все возрастающей неконкурентоспособности. Шухарт разработал простой способ классификации вариабельности процесса. Эта классификация служит первым шагом на пути уменьшения вариации продукции.
Д-р Шухарт рассматривал вариабельность с точки зрения того, находится ли она внутри некоторых пределов, определяемых случаем, или вне их. Если вне, считал он, то источник вариабельности можно определить:
Любые процессы подвержены вариабельности, но некоторые из них обладают управляемой вариабельностью, а некоторые — неуправляемой.
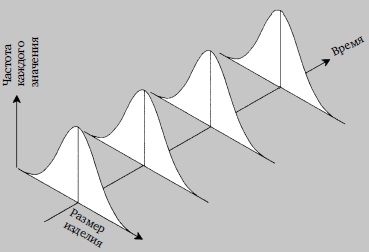
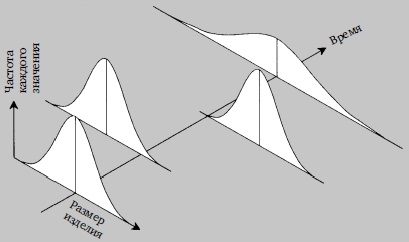
Управляемая вариабельность характеризуется тем, что ее структура стабильна и устойчива во времени. Д-р Шухарт объяснял такую вариабельность действием «случайных» причин (рис. 3). Неуправляемая вариабельность характеризуется тем, что ее структура переменна во времени. Д-р Шухарт объяснял такую вариабельность действием причин, какие могут быть установлены (рис. 4).
Рис. 3. Пример управляемой вариации
Рис. 4. Пример неуправляемой вариации
Явление следует называть управляемым тогда, когда, используя прошлый опыт, мы можем предсказать, по крайней мере в некоторых пределах, каких его вариаций можно ожидать в будущем.
Согласно классификации Шухарта, есть два разных пути улучшения производственного процесса. С одной стороны, если процесс демонстрирует управляемую вариацию, его следует воспринимать как стабильный и устойчивый. Вариация, присутствующая в процессе, отражает только то, что присуще самому процессу. Следовательно, чтобы снизить вариацию, нужно изменить сам процесс! Говоря словами Шухарта,
состояние управляемости — некий предел, которого мы можем стремиться достичь экономически выгодными методами, выявляя и ликвидируя причины вариабельности, не меняя основу… процесса.
С другой стороны, если процесс демонстрирует неуправляемую вариацию, то он время от времени изменяется. Он и неустойчив, и нестабилен во времени. Эта нестабильность создает избыточную вариацию, которая не имеет ничего общего с нормальным режимом работы процесса. Следовательно, первым шагом на пути улучшения поведения «выхода» процесса служит определение особых причин излишней вариации. Если особая причина наносит ущерб, ликвидируйте ее. Если она приносит выгоду, сделайте ее частью процесса. Шухарт дает несколько примеров того, как удаление наносящих ущерб специальных причин ведет к последовательному улучшению поведения процесса.
Заметим, что эти два подхода к улучшению процесса принципиально различны. Один из них выглядит механизмом улучшения устойчивого и хорошо организованного процесса, другой сам создает устойчивый процесс.
В качестве философского принципа производства инженерная концепция вариации не имеет ничего общего с концепцией Шухарта. У них разные цели и разные результаты. Цель инженерной концепции — соответствие допускам. В итоге характеристики изделия могут сколь угодно варьировать внутри установленных допуском пределов: все, что внутри, считается «достаточно хорошим». Цель концепции Шухарта — устойчивость процесса, в результате характеристики продукции получаются близкими, насколько это возможно. Следовательно, поиски компромисса между этими концепциями не имеют никакого смысла. Менеджмент просто должен выбрать одну из них. Японский опыт доказал эффективность постоянного улучшения производственных процессов.
Возможно четыре состояния, в которых находится любой производственный процесс.
- Идеальное состояние – процесс управляем и 100% продукции соответствует допускам.
- Пороговое состояние – процесс управляем, но не 100% продукции соответствует допускам.
- На грани хаоса – процесс неуправляем, хотя вся выпускаемая продукция соответствует допускам.
- Состояние хаоса – процесс неуправляем, и периодически производится брак.
Энтропия постоянно воздействует на все процессы, вызывая ухудшение качества, разрушение, износ и разрывы, аварии и отказы.
Статистическое управление процессами (SPC, Statistical Process Control) в конечном счете — это образ мышления, использующий контрольные карты в качестве катализатора мыслительного процесса.
Глава 2. Свертка данных
Свертка данных — это способ выудить из таблицы с цифрами наиболее любопытную информацию, пропустив все ненужные подробности (в оригинале было Summarizing Data, что лучше было бы перевести, как сводка данных; я оставил, как у переводчика. — прим. Багузина). В этой главе мы определим наиболее общие меры положения и рассеяния данных, а также проиллюстрируем некоторые из наиболее мощных графических инструментов свертки и анализа данных.
Меры положения. Среднее — это наиболее общая мера положения множества чисел, показывающая «центр масс» этих значений, точку его равновесия. Если элементы выборки обозначить через X, то среднее будет обозначаться X̅. Медиана определяет так называемый 50-й процентиль данных. Одна половина данных больше или равна медиане, другая половина — меньше или равна медиане. В то время как среднее показывает точку равновесия, медиана делит ряд данных пополам. Медиана обозначаться X̃.
Меры рассеяния. Размах — это разность между наибольшим и наименьшим значениями и обозначается символом R. Так как размах зависит только от двух значений, его очень легко вычислять. К сожалению, размах практически не отражает «срединных» значений, поэтому он неэффективен для описания больших массивов данных и используется для описания множеств, число элементов которых не превосходит 15.
При вычислении корня из среднего квадрата отклонения sn, в отличие от размаха, используется вся информация об имеющихся данных. Для ряда, состоящего из n элементов:
Стандартное отклонение рассчитывается по формуле:
Несмотря на то что некоторые учебники говорят о применении s для «генеральных совокупностей», а sn — для выборок, и то, и то — статистики, они обе — просто арифметические функции данных. (В Excel есть две функции: СТАНДОТКЛОН.В – оценивает стандартное отклонение по выборке, и использует в формуле знаменатель (n – 1); СТАНДОТКЛОН.Г – вычисляет стандартное отклонение по генеральной совокупности, и в знаменателе – n. Подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?)
Помимо численных методов свертки данных, существует и целый ряд графических. Гистограмма — это такой вид графика, при котором вдоль одной из координатных осей откладываются значения переменной, а вдоль другой — их частоты. Графики всегда служат наиболее мощным и эффективным способом передачи информации, содержащейся в данных. Численные обобщения могут дополнять гистограммы или графики хода процесса, но никогда не заменят их.
График «стебель и листья» служит еще одной формой отображения сгруппированных данных, показывающей в отличие от обычной гистограммы не только частоту попадания значения в заданные интервалы, но и сами значения (подробнее см. Как упорядочить массив данных).
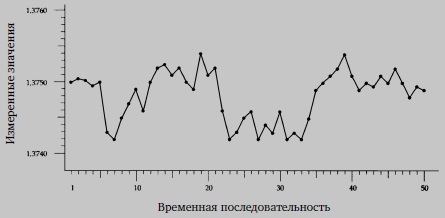
В описанных выше методах отсутствует один аспект анализируемых данных, а именно очередность их появления. Между тем временная последовательность данных очень важна во многих ситуациях, поэтому нужна графическая свертка таких данных. График хода процесса — как раз то, что надо (рис. 5).
Рис. 5. График хода процесса для размера подшипника распределительного вала
Глава 3. Контрольные карты Шухарта
Контрольные карты решают не те вопросы, какие ставятся обычно перед статистическими процедурами. Вместо того чтобы искать теоретическую модель для данных, полученных для какого-нибудь хорошо определенного явления, с помощью контрольной карты решают, можно ли использовать последовательность данных для предсказания того, что произойдет в будущем.
Когда предсказание возможно и делается подходящим образом, контрольные карты становятся основой такого предсказания. Когда же предсказание невозможно или непригодно из-за неуправляемой вариации, контрольные карты предупредят об этой нестабильности.
Рассмотрим некое явление, генерирующее поток чисел. Как можно использовать этот поток чисел для выводов о самом явлении? Шухарт предложил выделять подгруппы. Если к некоторому моменту времени сделано несколько измерений, их результаты можно сгруппировать и рассматривать как отдельное множество данных.
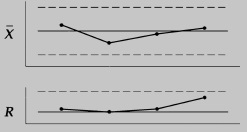
Предположим, что процесс стабилен во времени (статистически управляем). Пусть кривые, (рис. 6), отражают общий выход процесса каждый час. Так как процесс стабилен, эти кривые остаются во времени неизменными, час за часом. Если каждый час отбираются четыре изделия, и они измеряются, то в разных подгруппах будут получены различные результаты. Пусть крестики (×) показывают эти результаты. По каждой подгруппе вычисляются статистические свертки — групповое среднее и групповой размах. Эти итоговые статистики наносятся затем на контрольные карты (рис. 7). Эти контрольные карты представляют собой графики хода процесса с отмеченными на них контрольными пределами.
Рис. 6. Четыре подгруппы, отобранные из идеального стабильного процесса
Рис. 7. Карта среднего и размаха для стабильного процесса
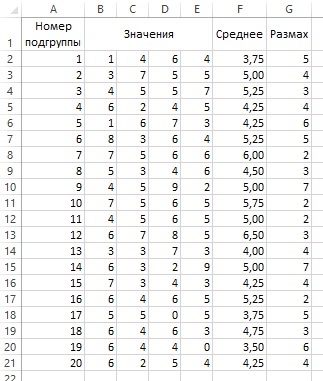
Рассмотрим расчет контрольных границ на примере. Измерения (рис. 8; см. также Excel-файл) — это толщины деталей. Приведенные числа показывают число тысячных дюйма, на которое превышено значение 0,300 дюйма.
Рис. 8. Измерение толщины деталей: 20 подгрупп по 4 измерения
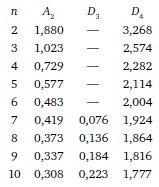
Контрольные пределы рассчитываются так. Непосредственно из данных: среднее средних X̿ = 4,7625; средний размах R̅ = 4,05; объем подгруппы n = 4. Из табл. на рис. 9: A2 = 0,729, D3 = 0 и D4 = 2,282.
Получаем:
UCLX̅ = X̿ + A2R̅ = 4,763 + 0,729 · 4,05 = 7,715 – верхняя граница карты средних;
CLX̅ = X̿ = 4,763 – центральная линия карты средних;
LCLX̅ = X̿ – A2R̅ = 4,763 – 0,729 · 4,05 = 1,811 – нижняя граница карты средних;
UCLR = D4 R̅ = 2,282 · 4,05 = 9,24 – верхняя граница карты размахов;
CLR = R̅ = 4,05 – центральная линия карты размахов;
LCLR = D3 R̅ = (не существует для n = 4) – нижняя граница карты размахов.
Рис. 9. Константы для расчета контрольных границ карт среднего и размаха, основанные на среднем
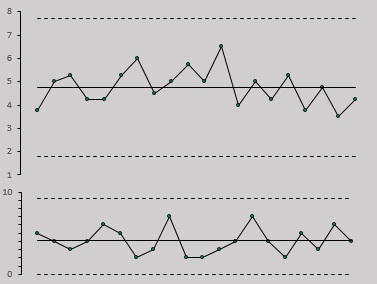
Рис. 10. Карта среднего и размаха для данных о толщинах деталей (построение этой карты можно найти в Excel-файле)
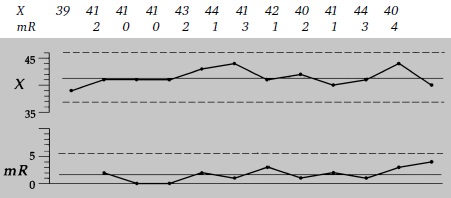
При n = 1 нельзя вычислить групповой размах, поэтому строится карта индивидуальных значений и скользящих размахов. Допустим, у нас есть 12 измерений (рис. 11). Внизу на строку ниже запишем размах между вторым измерением и первым, третьим и вторым, и т.д.
Рис. 11. Исходные данные, расчет границ и ХmR-карта (mR – скользящее среднее)
Глава 4. Теория и мифы контрольных карт
При расчете контрольных границ сначала следует вычислить средние значения и стандартные отклонения для подгрупп, и лишь затем на их основе находить среднее средних и среднее стандартное отклонение. Неправильное построение контрольных границ может быть связано с использованием для расчета стандартного отклонения s:
- всех индивидуальных значений
- средних значений подгрупп
Неправильные методы используют единственную статистику рассеяния. Правильные же методы основаны на применении средней из двух статистик рассеяния. Использование среднего статистик рассеяния — это один из фундаментальных принципов контрольных карт Шухарта.
Решение применять трехсигмовые пределы на контрольных картах не было основано только на теории вероятностей. Этот момент регулярно не понимается теми, кто пытается использовать теорию вероятностей для «корректировки» пределов контрольных карт.
Поскольку находящиеся в управляемом состоянии данные демонстрируют по определению разумную однородность, трехсигмовые пределы (вмещающие почти 100% всех точек) редко поднимают «ложную тревогу». В то же время, если некая точка оказывается за трехсигмовыми пределами, то это, скорее всего, обусловлено появлением особых причин. Например, если случайная величина распределена по нормальному закону, 99,7% всех точек будут в пределах трехсигмовой окрестности центральной линии (подробнее см. Нормальное распределение. Построение графика в Excel. Концепция шести сигм).
Контрольные карты будут хорошо работать даже в том случае, если данные не распределены по нормальному закону. И даже в том случае, когда распределение измеренных величин подчиняется закону, отличающемуся значительной асимметрией или «тяжелыми хвостами», число «фальшивых сигналов» о возникновении неустойчивости не становится чрезмерным. Следовательно, вне зависимости от того, как ведут себя данные, любые выбросы, по всей вероятности, свидетельствуют о появлении особых причин нестабильности процесса. Итак, карты средних и размахов робастны [1] по отношению к тем отклонениям от нормальности, которые встречаются на практике.
Мифы о картах Шухарта. Первый миф. Говорят, что контрольные карты можно использовать только для нормально распределенных данных. Миф о нормальности — следствие непонимания отношений между контрольной картой и методами статистического вывода. Как отмечал Шухарт, «нам безразлична функциональная форма генеральной совокупности, нам достаточно того, что она существует».
Второй миф. Говорят, что контрольные карты работают благодаря центральной предельной теореме. В случае, когда мы практически насильно «запихали» в контрольные пределы от 99 до 100% данных, нет надобности апеллировать к каким бы то ни было теориям, чтобы понять, что точка, выпадающая из этой группы, скорее всего, служит сигналом о нарушении стабильности процесса. Консервативная природа трех сигм делает центральную предельную теорему ненужной. Этот миф, несомненно, одно из главных препятствий на пути эффективного использования контрольных карт для анализа управленческих и промышленных данных. Всякий раз, когда есть только одно измерение в единицу времени, логично использовать подгруппы единичного объема (n = 1). Однако, если кто-то верит в миф о центральной предельной теореме, ему требуется каждый раз что-либо усреднить, чтобы получить ее благословение, и рациональность анализа данных будет принесена в жертву предрассудкам.
Третий миф. Говорят, что наблюдения должны быть независимыми — автокоррелированные данные неприемлемы для контрольных карт. Четвертый миф. Говорят, что процесс должен находиться в состоянии статистической управляемости, прежде чем наносить данные на контрольную карту.
Четыре «кита» карт Шухарта:
- Контрольные пределы карт Шухарта всегда устанавливаются на расстоянии три сигмы по обе стороны от центральной линии. Расчет контрольных 3σ-пределов всегда основывается на данных. Их нельзя определить с помощью вычислений, основанных на допусках. Трехсигмовые пределы — это пределы действия, они показывают, когда надо действовать в процессе. Они обеспечивают экономический баланс между двумя видами ошибок, которые можно сделать при интерпретации данных процесса. Они никогда не поднимают слишком много ложных тревог и не пропускают слишком много сигналов.
- При вычислении трехсигмовых контрольных пределов всегда используется среднее статистик рассеяния. Выбор статистик рассеяния не так уж и важен: можно использовать размах, стандартное отклонение или корень из среднего квадрата отклонений.
- Концептуальной основой карт Шухарта служит рациональный отбор данных и правильное выделение подгрупп.
- Контрольные карты эффективны только тогда, когда организация правильно использует получаемые с их помощью знания. Если вы не можете адекватно отреагировать на предоставленное контрольной картой знание, SPC не будет столь эффективным инструментом в ваших руках, каким мог бы быть. Пока на предприятии есть великое множество внутренних барьеров и препятствий для использования контрольных карт, ничего не произойдет само собой. Вот почему многие из знаменитых 14 пунктов доктора Деминга связаны с этим основополагающим принципом (подробнее см. У. Эдвардс Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами).
Глава 5. Эффективное применение контрольных карт
Пока результаты остаются в пределах трех сигм и варьируют относительно центральной линии случайным образом, можно уверенно сказать, что наш процесс стабилен. Но что, если текущие данные не варьируют относительно центральной линии случайным образом? Что, если в текущих данных проявляется некоторая структура? Чтобы не обращать внимания на структуру, которая образуется по случайным причинам, следует определить критерии, какую структуру данных считать неслучайной.
Серии — одна из неслучайных структур в текущих данных. Если восемь или более точек подряд оказываются по одну сторону от центральной линии карты средних значений, они могут рассматриваться в качестве свидетельства устойчивого смещения среднего процесса, даже если все точки лежат внутри контрольных пределов
Четыре правила определения отсутствия управляемости (подробнее см. Контрольные карты Шухарта. Правила определения отсутствия управляемости):
- Выход одной точки за трехсигмовые пределы.
- Выход хотя бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за двухсигмовые пределы.
- Выход по меньшей мере четырех из пяти последовательных точек, лежащих по одну сторону от центральной линии, за пределы одной сигмы.
- Расположение по меньшей мере восьми последовательных точек по одну сторону от центральной линии.
В принципе, этот список бесконечен. Но добавление каждого нового критерия отсутствия управляемости увеличивает вероятность ложных тревог. Чем больше критериев используется, тем чаще возникает что-то, что кажется сигналом. Типичный путь характеризации данного набора правил обнаружения — вычисление средней длины серии (ARL) между ложными тревогами. При использовании правила 1 теоретическое расстояние между сигналами ложной тревоги на карте средних равно 370 подгруппам. Если правило 1 сочетается с правилом 4, то ARL = 153. Если одновременно применяются все четыре правила, то ARL = 92.
Хотя теоретическая величина, равная 92, вполне приемлема, дополнительные критерии будут ее понижать, доводя до неприемлемо малой величины. Поэтому, пока многие призывают к одновременному применению более дюжины критериев, авторы этой книги рекомендуют ограничиться правилами, описанными в этом разделе.
Важный аспект эффективного использования контрольных карт — их способность отвечать на правильные вопросы. Для этого способ распределения данных по подгруппам должен соответствовать структуре данных. Обычно это означает, что в каждую подгруппу следует группировать данные из некоторой «малой области» — пространства, времени, партии продукции, чтобы внутри подгруппы данные были как можно более однородными (подробнее см. Рациональная группировка данных при построении контрольной карты Шухарта).
Принципы группировки:
- Никогда сознательно не собирайте в одну подгруппу непохожие вещи. Например, количества обрезанного справа (одна операция) и слева (другая операция) не могут принадлежать к одной и той же подгруппе, так как эти два значения представляют два разных процесса. Их смешивание попросту скроет различия между ними. Напомним, что, в соответствии с эмпирическими правилами, 2/3 точек должны находиться в пределах полосы X̅±σ, а примерно 95% точек — в пределах X̅±2σ. Если же точки лежат чересчур плотно к центральной линии, это может свидетельствовать о неправильном разбиении на подгруппы.
- Минимизируйте вариацию внутри каждой подгруппы. Именно вариация внутри каждой подгруппы задает основной уровень шума для наших данных. Помните, что карта размахов отвечает за внутригрупповые различия.
- Максимизируйте возможную вариацию между подгруппами. Если существует какая-нибудь возможность того, что две вещи могут различаться, убедитесь, что они в разных подгруппах.
- Усредняйте шумы, а не сигналы.
- Обрабатывайте карту в соответствии с тем, как будете использовать данные
- Сформулируйте операциональное определение процедуры сбора данных. Вполне вероятно, что на свойства собранных данных существенно влияет смена наблюдателей. Систематическая, стабильная процедура измерения — важное условие получения качественных данных.
Глава 6. Воспроизводимость, стабильность и качество мирового класса
Самый простой и легкий способ оценить воспроизводимость стабильного процесса — построить гистограмму индивидуальных значений прямо с контрольной карты, и нанести границы допуска на горизонтальную ось (рис. 12).
Рис. 12. Гистограмма для толщины муфт (это те же муфты, что и в статье Рациональная группировка данных при построении контрольной карты Шухарта)
Помимо графических оценок воспроизводимости устойчивого процесса, есть и численные. Эти численные значения можно использовать независимо, но они становятся более эффективными, если их совместить с гистограммой. Естественные границы процесса (NPL) можно использовать для определения фактической воспроизводимости стабильного процесса. Их можно вычислить прямо из среднего средних и среднего размаха:
NPL для индивидуальных значений = X̿ ± 3σ(X) = X̿ ± 3R̅/d2
NPL — это «голос процесса», поэтому вполне естественно оценивать воспроизводимость, сравнивая NPL с полем допуска. Если естественные границы стабильного процесса полностью попадают в поле допуска, то можно сказать, что процесс находится в идеальном состоянии: он управляем и выпускает 100% годной продукции. Такой процесс и стабилен, и воспроизводим.
Индексы воспроизводимости — это простой способ выражения отношения «голоса процесса» к «голосу потребителя». Результат обычно выражается в безразмерных единицах или процентах. Один из вариантов расчета индекса воспроизводимости, обозначаемого символом Cp, — это деление расстояния между границами допуска на расстояние между NPL:
Ср = (Верхняя граница допуска – Нижняя граница допуска)/6σ(Х)
Заметим, что Cp — это поле допуска, выраженное в сигма-единицах и деленное на 6,0.
Существует еще одна величина, обозначаемая Cpk (и тоже называемая индексом воспроизводимости), определяемая как расстояние до ближайшей границы (в σ-единицах), деленное на 3,0:
Cpk = DNS/3
Здесь DNS (от англ., the distance to the nearest specification) – расстояние от среднего до ближайшей границы (в σ-единицах). Cpk характеризует центрированность процесса относительно допусков. По определению Cpk меньше или равным Cp. Причем равно только в случае, если распределение центрировано относительно границ допуска.
Если процесс статистически неуправляем, его индексы вопросизводимости не вычисляют. Так как они лишены прогностической ценности. Нестабильные процессы, в отличие от стабильных, непредсказуемы, и никакие вычисления и никакие манипуляции с данными не могут обойти этот факт.
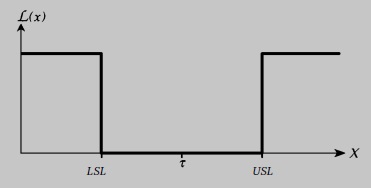
Качество мирового уровня. Вариация всегда порождает затраты. Традиционный подход к решению проблемы вариации неразрывно связан с понятием допуска (рис. 13). Однако пределы допуска — это на самом деле искусственные границы, которые используются для произвольных решений о том, как будет работать изделие.
Рис. 13. Функция потерь L(x) для концепции соответствия допуску; здесь τ – номинал, а LSL и USL – нижняя и верхняя границы допуска соответственно
Если следовать концепции допусков, вполне естественно пренебрегать вниманием к вариации в благоприятный период и резко повышать свой интерес к процессу, лишь когда он выходит за пределы допуска. В благоприятные периоды глубокое понимание процесса обычно теряется, совершенствование процесса не производится, а качество продукции начинает уходить от номинала снова и снова. Вот почему концепция допусков теперь уже не конкурентоспособна в сегодняшнем мире. Она не порождает постоянства цели настойчиво учиться у процесса и непрерывно его совершенствовать. Пока соответствие допускам рассматривается как главная цель любой операции, непрерывное улучшение процесса невозможно.
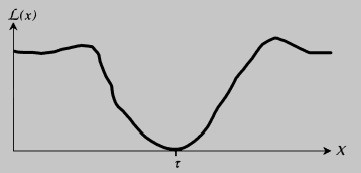
В 1960 г. доктор Генити Тагути предложил весьма элегантный подход к решению проблемы вариации (рис. 14). Простейший вид функции потерь — это:
L(x) = К(х — τ)2, где K — некоторая константа.
Рис. 14. Функция потерь Тагути
Несмотря на то, что реальная функция потерь может быть значительно более сложной, чем рассмотренная выше, этой аппроксимации должно быть вполне достаточно, чтобы описать потери в окрестности τ.
Представим, что нам известна функция плотности вероятностей f(x) некоего процесса. Тогда эта функция определит вероятность каждого из значений X, отложенных на горизонтальной оси. А функция потерь будет определять потери, L(x), соответствующие каждому X. Следовательно, средние потери на единицу продукции можно найти интегрированием произведения L(x) и f(x). Этот интеграл называется ожидаемым значением L(x):
где интегрирование ведется по всем Х. Если вместо L(x) использовать функцию потерь Тагути K(x – τ)2, то уравнение для средних потерь можно переписать следующим образом:
E = K[σ2 + (μ – τ)2],
где σ2 — квадрат стандартного отклонения (или дисперсия) распределения X, (μ – τ)2 — это квадрат смещения распределения Х, μ – среднее значение f(X). Этот результат не зависит от формы распределения Х. Таким образом, если процесс абсолютно стабилен, средние потери на единицу продукции можно выразить через параметры распределения X. В частности, можно заметить, что средние потери, обусловленные вариацией, пропорциональны квадрату стандартного отклонения (т.е. дисперсии) и квадрату величины, на которую среднее процесса отклоняется от номинала. Это означает, что средние потери будут всегда минимальны, если работать в номинале с минимальной дисперсией.
Концепция доктора Тагути, основанная на анализе функции потерь, неизбежно ведет к новому определению понятия качества мирового класса: точно в соответствии с номиналом при минимальной дисперсии!
Глава 7. Применение контрольных карт для непрерывного улучшения
В любой компании возможность начать перемены зависит от корпоративной культуры. Если менеджмент активно не поддерживает такие усилия, результата не будет. Иные специалисты внедряют изменения спорадически и непоследовательно. Иногда же изменения возможны, только если информация получена и понята правильными людьми.
Таким образом, сила контрольных карт зависит от того, насколько эффективно компания использует уникальную способность контрольных карт проникать в самую суть процессов. Если эта способность используется полностью, пределов для улучшения процесса практически нет. Проходя шаг за шагом через один или несколько циклов, контрольная карта будет непрерывно отслеживать процесс и накапливать информацию о его природе, позволяя осуществлять непрерывные улучшения.
Если же информация, предоставляемая контрольной картой, используется неэффективно, бесконечный цикл совершенствования разрывается. Такие разрывы позволяют энтропии разрушить процесс и, так как при этом продолжают появляться все новые и новые особые причины, бессистемные улучшения не помогут справиться с негативными факторами. Процесс медленно деградирует.
Далее приведен большой пример использования ККШ для непрерывного совершенствования процесса производства автомобильного прикуривателя.
Не стоит пытаться устанавливать цель для нестабильного процесса — неизвестно, на что он способен. Точно так же не стоит пытаться устанавливать цель для стабильного процесса — он уже достиг всего, на что он способен. Задание целей менеджерами — это обычно способ переложить ответственность на других, когда они не знают, как изменить нечто.
Глава 8. Установка цели процесса
«Цель процесса» — это то значение или значения, на которые процесс настроен. Таким образом, цель — это параметр, который корректирует оператор при настройке. «Среднее процесса» — это среднее значение некоторой характеристики продукции, усредненной для всей продукции, произведенной при заданной цели. «Номинал» — это желаемое значение среднего. Проще говоря, цель — это то, что вы задали, среднее — то, что вы получили, а номинал — то, что хотели получить. Суть процедуры наладки — задать цель так, чтобы среднее оказалось достаточно близко к номиналу. Процедура установки цели процесса будет совершенно бесполезной, если процесс статистически неуправляем.
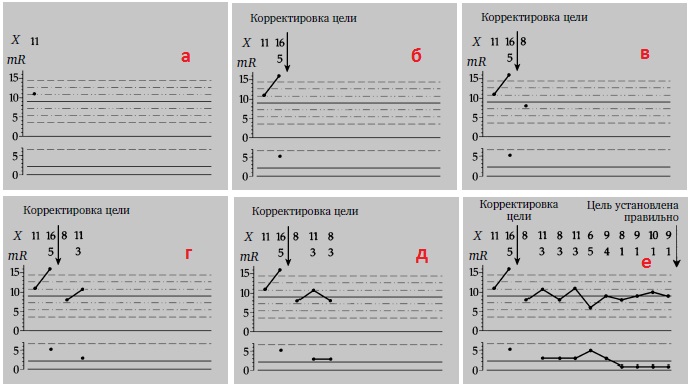
При установке цели процесса мы будем работать с картой индивидуальных значений. Карта скользящих размахов в данном случае представляет лишь дополнительную информацию. На карту индивидуальных значений наносим верхнюю и нижнюю естественные границы процесса, верхний и нижний 2σ-пределы и 1σ-пределы, а также центральную линию (рис. 15).
Рис. 15. Установка цели; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Первое значение равно 11 (а). Само по себе это значение ничего не говорит об отклонении среднего от номинала, поэтому никакие действия не предпринимаются. Второе значение равно 16 (б). Оно явно свидетельствует о потребности в корректировке цели. Среднее из двух значений определяет величину поправки: (11+16)/2 = 13,5. Цель процесса сдвинута вниз примерно на 4 единицы. Следующее после корректировки значение равно 8 и наносится на карту (в). В этот момент карта не показывает необходимости корректировок. Следующее значение равно 11 (г). Ни само это значение, ни его объединение с предыдущим не указывает на потребность в дальнейшей корректировке. Следующее значение равно 8 (д). Оно наносится на карту. Оно также находится вблизи от центральной лини и, поэтому коррекция не нужна. Последующие семь значений равны 11, 6, 9, 8, 9, 10 и 9 (е). Ни одно из них не свидетельствует о необходимости дальнейшей корректировки.
Корректировка цели процесса всегда будет ошибочной, если не получен четкий сигнал, что среднее процесса отклонилось от номинала.
Глава 9. Особенности контрольных карт для непрерывных переменных (факторов)
Неадекватные единицы измерения. Избыточное округление измерений может привести к тому, что контрольная карта укажет на выход процесса из-под статистического контроля даже в том случае, если процесс стабилен. Если внутри контрольных пределов лежат всего 1, 2 или 3 возможных значения размахов, то единицы измерения слишком велики для целей этой контрольной карты. Если округление слишком грубое, большая часть информации о рассеивании теряется при округлении. Проблема неадекватных единиц измерения (начинает негативно влиять на контрольную карту тогда, когда единица измерения превосходит стандартное отклонение процесса.
Когда стоит использовать XmR-карту? Чтобы понять, когда использовать XmR-карту, полезно различать две категории данных для контрольных карт: 1) регулярно собираемые и 2) периодически собираемые. Периодически собираемые данные — первые кандидаты для использования при построении XmR-карты. Вместо того чтобы ждать, пока пройдут два или больше интервалов времени между последовательными подгруппами, мы просто можем наносить на XmR-карту одно измерение за другим. Таким образом, периодически собираемые данные естественным образом представляются в виде подгрупп с n = 1. О том, как правильно строить карту индивидуальных значений и размахов см. Пример построения контрольной карты Шухарта в Excel.
Трехсторонние контрольные карты. На практике часто приходится иметь дело с данными, описывающими процессы с более чем одним источником вариации. Ранее мы рассматривали данные о параметрах шаровых муфт, содержащие несколько источников вариации, и эти данные наносились на контрольную карту тремя различными способами (см. Рациональная группировка данных при построении контрольной карты Шухарта). Если, например, собирать данные о прочности на разрыв образцов стали бессмысленно ожидать, что различные партии будут так же однородны, как и одна отдельно взятая партия. Использование внутригрупповой вариации для построения контрольных пределов неминуемо приведет к непомерному сужению контрольных пределов карты средних.
Итак, мы подходим к самому важному. Если резонно предположить, что вариацию от партии к партии можно уменьшить до уровня вариации в пределах одной партии, то традиционная контрольная карта средних и размаха — правильная. Если же уменьшить вариацию от партии к партии нельзя (для данного процесса), то эта контрольная карта может только ввести в заблуждение. Решение проблемы – в получении таких контрольных пределов, которые будут учитывать обычные вариации от партии к партии. Тогда карта размахов будет следить за вариацией внутри партии, а карта средних (с пересмотренными контрольными пределами) сможет отразить вариацию от партии к партии, если она превысит обычный уровень.
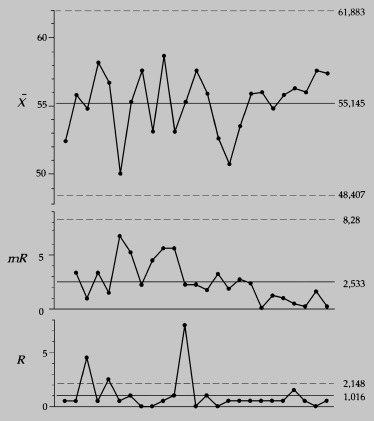
Наилучший способ установить вариацию от партии к партии — прямо измерить ее. Это можно сделать построением карты на основе групповых средних (группа = партии) и скользящих размахов. Карты средних и скользящих размахов непрерывно следят за вариацией от партии к партии, а обычная карта размахов — за внутригрупповой вариацией (рис. 16).
Рис. 16. Трехсторонняя контрольная карта для данных о прочности на разрыв стали
Обновление контрольных пределов. Как только вы найдете особые причины и ликвидируете их, вам потребуется собрать новые данные и заново рассчитать контрольные пределы. Как правило, контрольные пределы обновляются после перемен в процессе. Использовать контрольную карту только для подтверждения того, что уже известно, — не лучший путь ее применения. Карта нужна для познания неизвестного. Поэтому, если сделаны продуманные изменения процесса, вполне логично накопить новые данные и пересчитать контрольные пределы.
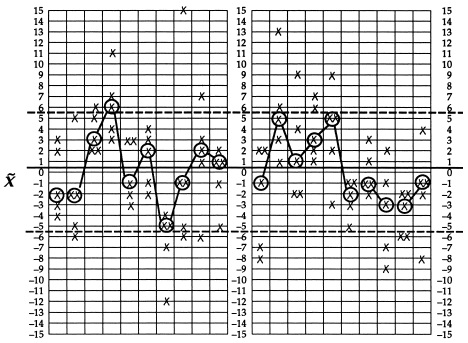
Карты для групповых медиан и групповых размахов. Карта медиан может использоваться, когда рабочие не могут (или не хотят) иметь дело с вычислениями для работы с картами средних и размахов. Карты медиан могут строиться непосредственно на листе бумаги (рис. 17). Однако карта медиан менее чувствительна и дает меньше сигналов, чем карта средних.
Рис. 17. Карты медиан для данных о весе резиновых деталей; здесь крестики – индивидуальные значения, а кружочки – медианы
Глава 10. Контрольные карты для дискретных величин
Большинство атрибутов (дискретных величин) можно успешно описывать обычными XmR-картами. Но можно использовать и контрольные карты, специально разработанные для атрибутов (p-, np-, c-, u-карты).
Глава 11. Эффективное использование дискретных величин
Сначала надо признать внутреннее несовершенство дискретных данных. Чем лучше процесс, тем больше должна быть область определения для получения чувствительных контрольных карт. Далее, дискретные данные не заменяют результатов измерений. Даже если шаблон «проходит — не проходит» можно использовать для эффективной 100%-ной проверки, он не дает удовлетворительных данных для использования в контрольных картах. Более того, всегда, когда можно использовать такой шаблон, возможны и измерения. Измерения нескольких изделий гораздо содержательнее, чем доля несоответствий в большой выборке. Наконец, третья общая характеристика дискретных данных заключается в том, что трудно идентифицировать вариацию из разных источников. Эта характеристика обусловлена внутренней структурой данных.
Брайан Джойнер перечисляет три способа достижения цепей: улучшение системы, искажение системы, искажение данных.
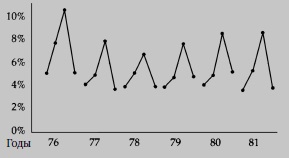
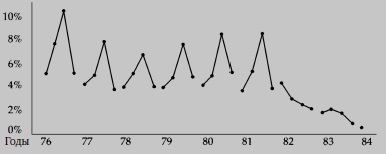
Одна компания, производящая крепления для мотора, постоянно сталкивалась с отказами из-за адгезии. Из каждой партии креплений некоторое число испытывалось на отказы. Значением, которое определялось в этом испытании, было усилие, при котором наступает отказ. Квартал за кварталом испытания показывают, что не менее 4% опор отказывают при расчетной нагрузке. Эти результаты становятся еще хуже весной и летом. Такой высокий уровень сохраняется годами, несмотря на те многократные усилия, что предпринимали инженеры в надежде на улучшения (рис. 18).
Рис. 18. Процент отказов при расчетной нагрузке за 1976-1981 гг.
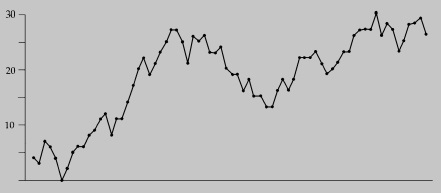
Компания по производству креплений начала внедрять методы, приведенные в этой книге, в конце зимы 1982 г. Уже весной того же года только 3% креплений отказали при той же нагрузке. А к лету отказы снизились до 2,5%. Такое непредвиденное улучшение привлекло всеобщее внимание. Когда директор завода спросил, что было сделано, инженеры и мастера не смогли сказать ничего конкретного. Единственным явным изменением было использование контрольных карт на каждом шаге производства. Эти карты показали, что на каждом шаге процесса была слегка снижена вариация. Снижение доли отказов стало результатом кумулятивного действия этих уменьшенных вариаций. Более того, улучшения продолжались и в следующих кварталах (рис. 19).
Небольшие, но постоянные улучшения на каждом шагу производственного процесса дают эффект. Как только вариация снизится на одном шаге, улучшать следующие шаги становится легче. Материал, поступающий на каждую стадию, имеет меньшие средние потери по Тагути. Это позволяет тратить меньше времени на подготовку процесса к работе и больше — на улучшение процесса. При продолжении этого цикла сквозь весь процесс конечный продукт можно существенно улучшить.
Рис. 19. Процент отказов при расчетной нагрузке за 1976-1984 гг.
Эти рисунки — это карты-отчеты. Фактически они не указывают причину перемен, имеющих место. Тем не менее они отмечают кумулятивный эффект улучшения, достигнутый благодаря контрольным картам на каждом из 14 шагов процесса. Информация на этих рисунках слишком обобщена, чтобы указать на конкретные проблемы. Наконец, заметим, что в этом процессе не было никакой «магической пилюли». Не было ничего, что надо было бы изменить для улучшения результатов. Вместо этого надо было делать все то же самое, только с меньшей вариацией. Все это стало возможным благодаря эффективному использованию контрольных карт на каждом шаге процесса.
Глава 12. Начало работы
Поскольку большинство проблем в промышленности возникает из-за неясной структуры факторов, влияющих на процесс, первый шаг к использованию данных заключается в том, чтобы выбрать переменные для мониторинга. Такой выбор легче сделать с помощью одного или нескольких из трех основных графических методов: блок-схемы, диаграммы причин и результатов и диаграммы Парето.
Блок-схемы — это инструменты визуализации процесса. Блок-схемы жизненно важны на первом этапе процесса непрерывного совершенствования, поскольку они помогают понять процесс, который мы хотим улучшить.
Диаграмма причин и результатов впервые была применена в связи со статистическим управлением процессами в Японии. Доктор Каору Исикава обнаружил, что многих сотрудников предприятий пугает большое число факторов, которые могут повлиять на продукцию или процесс. Поэтому в 1950 г. он начал использовать «дерево отказов» для решения проблем. Этот подход оказался столь эффективным, что мгновенно распространился по всей Японии. Гибкость диаграммы делает ее полезным инструментом решения проблем в любой области производства или обслуживания.
Хотя эту диаграмму и называют «рыбьим скелетом», завершенная диаграмма вовсе не похожа на скелет рыбы. Если она будет похожа на скелет, это означает, что диаграмма построена плохо, так как указание только базовых факторов без детализации не дает возможности определить, с чего начать улучшения.
Диаграмма Парето — еще один простой инструмент, помогающий сосредоточить усилия на проблемах, имеющих наибольший потенциал для улучшений. Поскольку ресурсы у всех компаний ограниченны, очевидно, что следует направлять их на решение самых важных проблем. Она была названа в честь Парето, который сформулировал «принцип Парето»: 20% проблем дают 80% головной боли. Другими словами, основные возможности для улучшений обычно связаны с очень малым числом проблем. И именно эти проблемы и нужно решать организации в первую очередь (подробнее см. Семь основных инструментов контроля качества).
Глава 13. Вопросы дальнейших исследований
В дополнение к среднему и стандартному отклонению набора данных некоторые специалисты используют также асимметрию и эксцесс. Параметр асимметрии измеряет относительный размер двух хвостов. У симметричных распределений параметр асимметрии равен нулю. Если правый хвост тяжелее левого, то параметр асимметрии будет положительным. А если тяжелее левый хвост — отрицательным. Более того, чем больше разница между хвостами, тем больше будет величина параметра асимметрии.
Параметр эксцесса измеряет совместный вес хвостов относительно остального распределения. По мере утяжеления хвостов распределения эксцесс будет расти. А по мере их облегчения — уменьшаться (у нормального распределения эксцесс равен 3).
Шухарт отказался от использования этих статистик. Он писал, что статистики положения и рассеивания дают практически все, что полезно, все, что можно извлечь из численных сводок данных. Использование дополнительных статистик, таких как асимметрия и эксцесс, излишне.
Влияние вариации на сбалансированные системы. Цель балансировки системы заключается в согласовании мощностей различных шагов (или стадий), с тем чтобы нигде в системе не было избыточной мощности. К сожалению, объекты никогда не работают точно так, как запланировано. Всегда есть некоторая вариация.
До тех пор, пока операции замкнуты и зависят друг от друга, некоторое количество материалов, поступивших на вход процесса, неизбежно создаст запасы в процессе. По мере накопления в процессе незавершенной продукции, эти запасы будут стремиться разъединить операции процесса, благодаря чему эти операции смогут выполняться независимо друг от друга. В этот момент произойдут две вещи. Случайные простои, которые неизбежны, когда операции зависят друг от друга, исчезнут, а выход процесса будет расти до состояния средней мощности сбалансированных шагов (подробнее см. Моделирование в Excel сбалансированной производственной линии). Пока запасы в процессе не вырастут до уровня, который сделает операции независимыми, выход системы всегда будет ниже, чем средняя мощность отдельных шагов (рис. 20).
Рис. 20. Запасы в процессе за 72 цикла (моделирование)
Один из способов обойти накопление запасов в процессе — это увеличение средней мощности некоторых операций, — так, чтобы только одна из операций оставалась узким местом. Если поток материалов будет планироваться по узкому месту, запасов возникать не будет. Если спрос будет равен средней производительности для одного узкого места, система сможет работать по графику (подробнее см. Моделирование в Excel производственной линии с участком–ограничением).
Библиография на русском языке
Исикава К. Японские методы управления качеством. — М.: Экономика, 1988.
Нив Г. Организация как система: Принципы построения устойчивого бизнеса Эдвардса Деминга. — М.: Альпина Бизнес Букс, 2007.
Тьюки Дж. Анализ результатов наблюдений. Разведочный анализ. — М.: Мир, 1981
[1] Робастность (англ. robustness, от robust — «крепкий», «сильный», «твёрдый», «устойчивый») — свойство статистического метода, характеризующее независимость влияния на результат исследования различного рода выбросов, устойчивости к помехам.
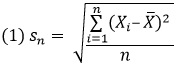
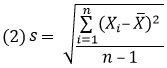

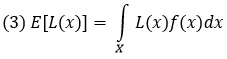
Сергей, здравствуйте! Подскажите: насколько, по Вашему мнению, применимы идеи Шухарта-Деминга для анализа и повышения эффективности работы торговой компании (продажа промышленно оборудования)? Есть ли подходящие примеры из Вашей практики?
Мне кажется, что продажи имеют сходство например с обработкой деталей на станках, т.к. оба процесса имеют цикличную природу и подвержены влиянию случайности. И в обоих случаях наступает момент, когда кнут и пряник становится бесполезен (для рабочих и менеджеров по продажам) и возникает необходимость в улучшении системы.
Спасибо!
Николай, я работаю в оптовой торговой компании, и по мере сил использую ККШ в повседневной практике. В качестве примера см.
Управление логистическими издержками с использованием контрольных карт Шухарта. Полностью разделяю ваши взгляды на ограниченность «кнута и пряника», и стараюсь совершенствовать систему…Сейчас считаю работу сайта по этой формуле:
NPL для индивидуальных значений = X̿ ± 3σ(X) = X̿ ± 3R̅/d2
Смотрю как меняется посещаемость, отказы на сайте и тд. Играюсь.
Но не могу понять когда и нужно ли использовать другую формулу:
UCLX̅ = X̿ + A2R̅
CLX̅ = X̿
LCLX̅ = X̿ – A2R̅
UCLR = D4 R̅
CLR = R̅
LCLR = D3 R̅
Что вы посоветуете. Книгу сейчас читаю, но ответа пока не нашёл. Только начала. Можете мне помочь разобраться чуть ранее)
Владимир, на мой взгляд, использовать ККШ для анализа сайта не вполне корректно. Скорее, всего у вас присутствует сезонная составляющая, и иные естественные колебания, и тренды. Например, у меня посещаемость падает летом, а также в выходные дни. Кроме того, посещаемость растет из года в год. ККШ — инструмент принятия решения, когда процесс становится статистически неуправляемым. Какие решения вы хотите принять, если точки выйдут за границы!?
Сергей Викторович!
Подскажите пожалуйста, существуют ли какие либо курсы по статистическому управлению и инструментам статистического управления заслуживающие доверия?
Не продвигающие какой то конкретный программный продукт, а описывающие общие методики, проблематику и применимость + некий практикум.
Руслан, я не интересовался курсами. Но в Интернете они широко представлены.