Эта заметка основана на моем мастер-классе, проведенном в рамках конференции «Системный анализ в экономике», прошедшей 9–11 ноября 2016 г. в Финансовом университет при Правительстве РФ. Сохранен стиль выступления.
Позвольте вопрос: что вы понимаете под словами «системный подход»?
Наверное, следует начать с общей теории систем, получившей развитие в трудах Людвига фон Берталанфи, Норберта Винера, Уильяма Эшби, Стаффорда Бира. Теория систем — научная и методологическая концепция исследования объектов, представляющих собой системы. Основная идея теории состояла в признании изоморфизма законов, управляющих функционированием системных объектов, независимо от их природы. В настоящий момент, пожалуй, находится в упадке.
Скачать заметку в формате Word или pdf, скачать презентацию
Далее, я бы упомянул системную динамику — направление в изучении сложных систем, исследующее их поведение во времени и в зависимости от структуры элементов системы и взаимодействия между ними. В том числе: причинно-следственных связей, петель обратных связей, задержек реакции, влияния среды и других. Это направление получило развитие в работах Джея Форрестера, Денниса и Донеллы Медоуз, Питера Сенге. Особенное внимание уделяется компьютерному моделированию таких систем, в том числе и в экономике (см., например, Игорь Цисарь. Моделирование экономики в iThink_STELLA). На мой взгляд, пик интереса к теме пришелся на 60-е–70-е годы. Я считаю, что неточность прогнозов на основе моделирования связана с излишней самоуверенностью исследователей, которые берут слишком узкие рамки параметров модели.
Заслуживает упоминания также теория ограничений — популярная методология управления производством, разработанная в 1980-е годы Элияху Голдраттом, в основе которой лежит нахождение и управление ключевым ограничением системы, которое предопределяет успех и эффективность всей системы в целом. Основной особенностью методологии является то, что, управляя небольшим числом аспектов системы (в идеале – одним), достигается эффект, намного превышающий результат одновременного воздействия на все или большинство проблемных областей системы сразу.
И, наконец, предмет более подробного сегодняшнего обсуждения – статистическое управление процессами (SPC) – метод мониторинга производственного процесса с использованием статистических инструментов с целью управления качеством продукции «непосредственно в процессе производства». В дальнейшем парадигма была расширены на любые организации (не только производственные). Ключевым инструментом метода является контрольная карта Шухарта. Решающий вклад в разработку идей внес Уильям Э. Деминг.
Сегодняшнее обсуждение будет вращаться вокруг следующих тем:
- Менеджмент на основе статистического управления процессами
- Вариабельность
- Два типа управленческих ошибок
- Контрольные карты Шухарта
- Качество мирового уровня
Допустим, вы финансовый директор и изучаете логистические издержки, выраженные в процентах, как доля стоимости товаров. Перед вами данные по двум партиям товаров:
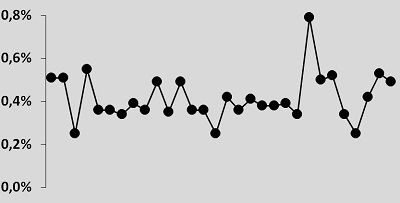
Что можно сказать о столь значительном (более, чем в два раза) различии? Возможно, ваша рука потянулась к телефону, чтобы «взгреть» нерадивых подчиненных… Но, если вы на минутку остановитесь, и попросите показать данные по последним 30 поставкам, то увидите следующую картину:
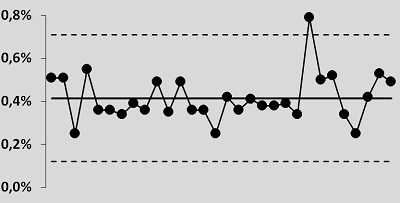
Точки, изображенные на первом рисунке, соответствуют третьей и четвертой точкам на этом рисунке. Ничего особенного! Точки лишь незначительно выделяются в ряду прочих, и есть одна точка, гораздо больше отклонившаяся от воображаемой средней линии (ближе к концу ряда).
Основная идея теории Шухарта очень проста: мир сложен, и точно предсказать результат большинства реальных процессов невозможно в принципе. Но для практики этого и не нужно: достаточно научиться предсказывать результаты с той степенью уверенности, которая экономически оправданна на данном этапе развития человечества и при данном уровне последствий принимаемых решений. Чтобы это сделать, следует принять во внимание, что большая часть результатов любого процесса определяется системой, в которой этот процесс проходит, и лишь небольшая их часть вызвана внешними по отношению к этой системе причинами.
Поэтому нам надо научиться определять, какие результаты принадлежат системе, а какие — внешним внесистемным силам. Результатами, обусловленными системой, можно управлять, только изменяя саму систему. Но сначала надо устранить все внесистемные воздействия, поскольку они по определению неуправляемы и, следовательно, непредсказуемы. Инструментом, помогающим понять, какие воздействия принадлежат системе, а какие нет, и служат контрольные карты Шухарта.
Шухарт предложил правила нанесения контрольных границ, которые отделяют сигнал от шума. Шухарт обнаружил, что система, если она находится в стабильном, управляемом, устойчивом состоянии, ведет себя так, что ее результаты можно предсказывать с определенной точностью до тех пор, пока что-то или кто-то не выведет ее из этого состояния. Такую систему принято называть статистически управляемой. Предсказуемость позволяет управлять процессом, а значит, и улучшать его. Без предсказуемости никакое совершенствование невозможно.
Под системным решением Шухарт предложил подразумевать основанный на теории вариабельности способ принятия решений о том, надо ли вмешиваться в процесс… и кому.
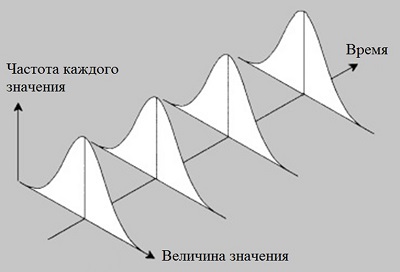
Если в момент времени t0 система демонстрирует некую вариабельность, например, как на рисунке выше, то и в последующие моменты времени при измерении параметров системы, мы будем наблюдать аналогичное распределение (в данном примере, нормальное).
Напротив, если есть какие-то внешние вмешательства в систему, то о предсказаниях можно забыть. Система становится не только непредсказуемой, но и неуправляемой. Тогда надо как можно быстрее выявить и устранить источник внешнего вмешательства и вернуть ее в управляемое состояние. Дело за малым. Нужно научиться различать состояния, в которых находится система, а затем решать, что и кому надо с ней делать (или не делать).
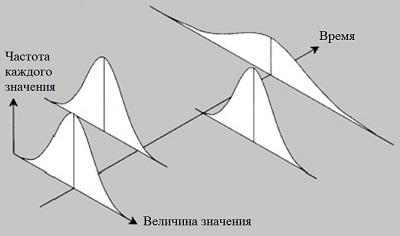
А здесь, то что в момент времени t0 система демонстрирует некую вариабельность, подчиняющуюся нормальному распределению, совершенно не гарантирует, что поведение во времени сохранится. В последующие интервалы времени система вполне способна показывать иные виды вариабельности.
Контрольные карты Шухарта — это и есть диагностический инструмент для ответа на вопрос: надо или не надо вмешиваться в систему, и если надо, то кому? Он построен с помощью статистических методов, но сам не имеет статистической природы. Это сделано для того, чтобы модели могли избежать «смирительной рубашки» теоретической статистики. В условиях накопления информации система может и сама служить себе эмпирической моделью, гораздо более естественной, чем теоретические модели, навязанные извне.
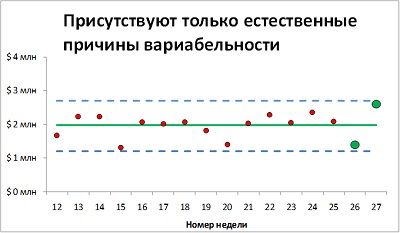
В июне 2015 г. «небывалый» всплеск рекламаций, поиск виновных и причин ухудшения ситуации. На самом деле процесс остается статистически управляемым. Контрольные карты меняют восприятие – мы не реагируем на шум, и ждем сигнала системы. Это не значит, что мы вовсе остаемся пассивными. Если вариабельность статистически управляемого процесса нас не устраивает, мы можем заняться совершенствованием системы, с тем чтобы изменить ее параметры. Но мы точно не будем искать виновного!
Вот еще один пример на эту тему. На 27-й неделе задолженность выросла почти в два раза по сравнению с предыдущей неделей: с $1,4 млн. до $2,6 млн. Мы видим, что показатели не требуют немедленного вмешательства.
Первая типичная ошибка менеджмента – отклонение параметра процесса приводит к поиску причин «аномального» значения. В то время, как это значение укладывается в рамки естественной вариации. Никто не виноват! Выявление причинно-следственной связи не требуется для объяснения данных. Точки укладываются в естественные границы процесса! Не нравятся отклонения, работайте над совершенствованием процесса (системы)!
Любопытный пример описан Демингом. На заводе Ford на станке был установлен компенсатор. После изготовления каждой детали, ее размеры измерялись, и, если они были больше или меньше номинала, то компенсатор изменял настройки станка в сторону, противоположную отклонению. Оказалось, что если не использовать компенсатор, то размеры партии деталей ложатся более кучно, чем с использованием компенсатора.
За рассуждениями У. Шухарта скрывались не столько статистика, сколько экономика и его соображения о том, оправдаются ли расходы, связанные с выявлением признаков неуправляемости процесса, теми выгодами, которые мы получим благодаря их обнаружению и устранению.
Давайте рассмотрим два примера иного рода, когда данные «кричат» о необходимости действий, но менеджмент не спешит вмешиваться…
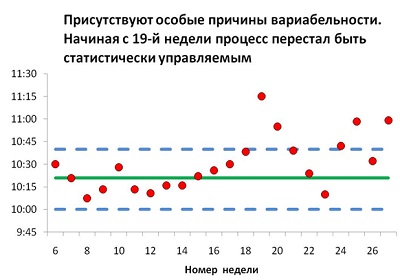
Задержки с отправкой машин со склада. Процесс был стабилен, но вышел из-под контроля, начиная с 19-й недели. Необходимы управленческие решения для возвращения процесса в статистически управляемое состояние. Однако, ни руководство, ни исполнители, не ищут причины проблем. (Оказалось, что из-за начала периода отпусков склад не успевал вовремя собрать грузы, поэтому их отправка и задерживалась.)
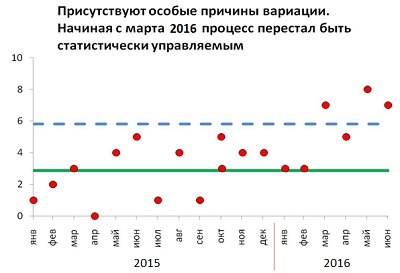
Число уволившихся. Процесс был стабилен с января 2015 по февраль 2016. С марта 2016 появились особые причины, приведшие к выходу показателя за контрольные границы.
Требуется найти причину и осуществить управленческое воздействие, чтобы вернуть ситуацию к управляемому состоянию. (Последующий анализ показал, что тарифная сетка давно не пересматривалась, и уровень заработных плат постепенно опустился ниже средней по рынку суммы.)
Вторая типичная ошибка менеджмента – отклонение параметра процесса не воспринимается как критически важное (как сигнал), и вместо принятия мер, менеджмент продолжает наблюдать за процессом.
Итак, что вы узнали (запомнили) о вариациях и управлении?
Я считал бы, что добился поставленной цели, если вы в том или ином виде укажете следующее:
- Всем процессам свойственны вариации
- Вариации могут быть обусловлены естественными и особыми причинами
- Для определения типа причины вариации используются контрольные карты Шухарта
- Пока показатель находится в пределах контрольных границ, процесс статистически управляем, вариации обусловлены естественными причинами, управленческое воздействие в ответ на конкретную вариацию может только навредить
- Если показатель выходит за контрольные границы, процесс перестает быть статистически управляемым, вариации обусловлены особыми причинами, требуется управленческое воздействие
Что дальше?
- Необходимо собирать информацию по критически важным процессам
- Строить контрольные карты
- Рассчитывать контрольные границы, чтобы отличать естественные и особые причины вариаций
- Выявлять и устранять особые причины вариаций
- Совершенствовать статистически управляемые процессы, чтобы уменьшать вариации
Какой смысл вы вкладываете в термин «качество мирового уровня»?
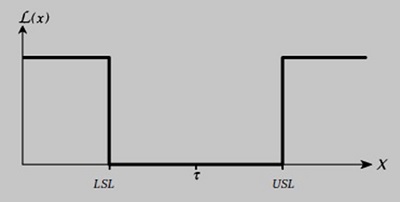
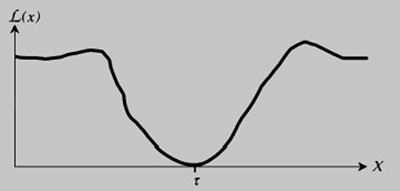
Традиционный подход к решению проблемы вариации неразрывно связан с понятием допуска. Однако пределы допуска — это на самом деле искусственные границы, которые используются для произвольных решений о том, как будет работать изделие. Функция потерь L(x) для концепции соответствия допуску:
здесь τ – номинал, а LSL и USL – нижняя и верхняя границы допуска.
Если следовать концепции допусков, вполне естественно пренебрегать вниманием к вариации в благоприятный период и резко повышать свой интерес к процессу, лишь когда он выходит за пределы допуска. На самом деле, понятие «допуска» может быть расширено за рамки производства. Например, установив норматив на некую процедуру – 2 часа, менеджмент может не обращать внимание на случай, когда процедура выполнена за 1 час 59 минут, и устраивать шумиху, в случае исполнения за 2 часа 3 минуты…
В благоприятные периоды глубокое понимание процесса обычно теряется, совершенствование процесса не производится, а качество продукции начинает уходить от номинала снова и снова. Вот почему концепция допусков не конкурентоспособна в сегодняшнем мире. Она не порождает постоянства цели настойчиво учиться у процесса и непрерывно его совершенствовать. Пока соответствие допускам рассматривается как главная цель любой операции, непрерывное улучшение процесса невозможно.
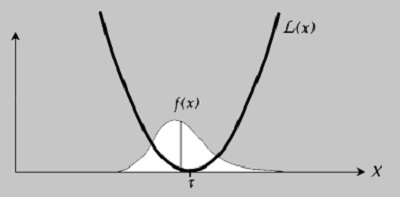
В 1960 г. доктор Генити Тагути предложил весьма элегантный подход к решению проблемы вариации:
Теперь функция потерь возрастает при увеличении отклонения от номинала: L(x) = К(х — τ)2, где K — некоторая константа.
Несмотря на то, что реальная функция потерь может быть значительно более сложной, чем рассмотренная выше, этой аппроксимации вполне достаточно, чтобы описать потери в окрестности τ. Представим, что нам известна функция плотности вероятностей f(x) некоего процесса. Тогда эта функция определит вероятность каждого из значений X, отложенных на горизонтальной оси. А функция потерь будет определять потери, L(x), соответствующие каждому X. Следовательно, средние потери на единицу продукции можно найти интегрированием произведения L(x) и f(x).
Концепция доктора Тагути, основанная на анализе функции потерь, неизбежно ведет к новому определению понятия качества мирового класса: точно в соответствии с номиналом при минимальной дисперсии!
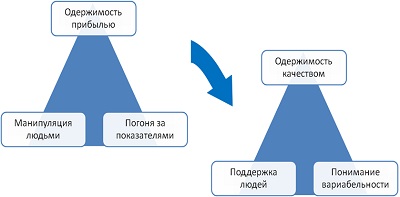
Если Уолтер Шухарт был инженером (статистиком), и свои идеи ориентировал в первую очередь на инженеров и технологов, то Доктор Деминг первым понял, что новый подход может быть реализован лишь при полной смене парадигмы управления:
Деминг предложил 14 принципов, которыми должен руководствоваться менеджмент компании, если хочет достичь качества мирового уровня. Вот некоторые из них:
- Цель — непрерывное улучшение
- Качество создается не проверкой, встраивайте качество в процесс.
- Изгоняйте страх, разрушайте барьеры между подразделениями.
- Устраните KPI, замените их лидерством.
- Создайте условия, которые позволят сотрудникам гордиться своим мастерством.
Рекомендованная литература:
Уильям Э. Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами.
Д. Уилер, Д. Чамберс. Статистическое управление процессами: Оптимизация бизнеса с использованием контрольных карт Шухарта.