Ранее была рассмотрена диаграмма разброса, иллюстрирующая распределение двумерных числовых данные (см. последний раздел Изображение двумерных числовых данных заметки Представление числовых данных в виде таблиц и диаграмм). В настоящей заметке мы изучим два количественных показателя, характеризующих силу зависимости между двумя переменными — ковариацию и коэффициент корреляции. [1] Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Рассмотрим пятилетнюю среднегодовую доходность и долю затрат в фондах с очень низким уровнем риска (рис. 1). Для расчета ковариации двух выборок в Excel до 2007 года используется функция =КОВАР(), начиная с версии 2010 – функция КОВАРИВЦИЯ.В().
Рис. 1. Пятилетняя среднегодовая доходность и доля затрат взаимных фондов с очень низким уровнем риска
Любопытно, что ковариация случайной величины с собой равна дисперсии:
Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.
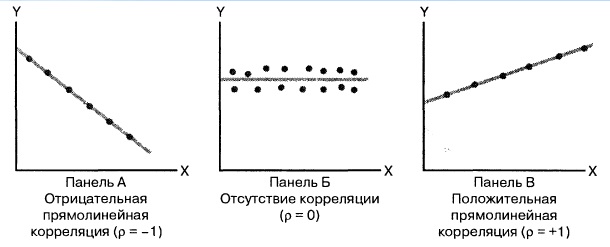
Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой (рис 2). На панели А изображена обратная линейная зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен –1, т.е., когда переменная X возрастает, переменная Y убывает. На панели Б показана ситуация, в которой между переменными X и Y нет корреляции. В этом случае коэффициент корреляции ρ равен 0, и, когда переменная X возрастает, переменная Y не проявляет никакой определенной тенденции: она ни убывает, ни возрастает. На панели В изображена линейная прямая зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен +1, и, когда переменная X возрастает, переменная Y также возрастает.
Рис. 2. Три вида зависимости между двумя переменными
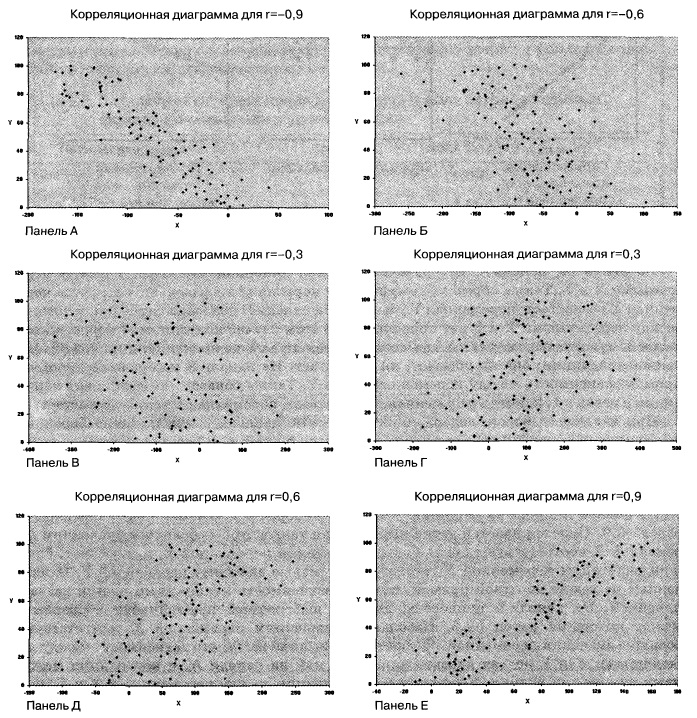
При анализе выборок, содержащих двумерные данные, вычисляется выборочный коэффициент корреляции, который обозначается буквой r. В реальных ситуациях коэффициент корреляции редко принимает точные значения -1, 0 и +1. На рис. 3 приведены шесть диаграмм разброса и соответствующие коэффициенты корреляции r между 100 значениями переменных X и Y.
Рис. 3. Шесть диаграмм разброса и соответствующие коэффициенты корреляции, полученные с помощью программы Excel
На панели А показана ситуация, в которой выборочный коэффициент корреляции r равен –0,9. Прослеживается четко выраженная тенденция: небольшим значениям переменной X соответствуют очень большие значения переменной Y, и, наоборот, большим значениям переменной X соответствуют малые значения переменной Y. Однако данные не лежат на одной прямой, поэтому зависимость между ними нельзя назвать линейной. На панели Б приведены данные, выборочный коэффициент корреляции между которыми равен –0,6. Небольшим значениям переменной X соответствуют большие значения переменной Y. Обратите внимание на то, что зависимость между переменными X и Y нельзя назвать линейной, как на панели А, и корреляция между ними уже не так велика. Коэффициент корреляции между переменными X и Y, изображенными на панели В, равен –0,3. Прослеживается слабая тенденция, согласно которой большим значениям переменной X, в основном, соответствуют малые значения переменной Y. Панели Г–Е иллюстрируют положительную корреляцию между данными — малым значениям переменной X соответствуют большие значения переменной Y.
Обсуждая рис. 3, мы употребляли термин тенденция, поскольку между переменными X и Y нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и Y, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.
Выборочный коэффициент корреляции:
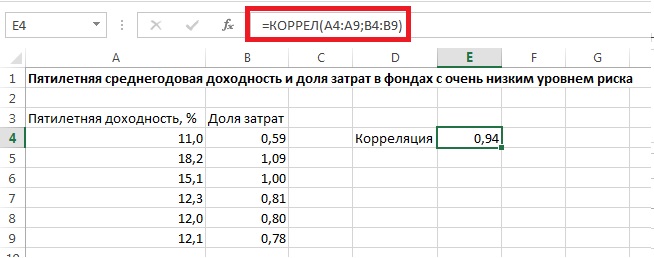
В Excel для вычисления коэффициента корреляции используется функция =КОРРЕЛ() (рис. 4).
Рис. 4. Функция КОРРЕЛ в Excel
Итак, коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.
Предыдущая заметка Анализ данных. Пять базовых показателей распределения случайной величины
Следующая заметка Основные понятия теории вероятностей
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 221–227
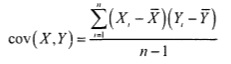

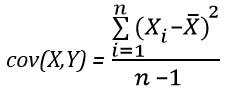
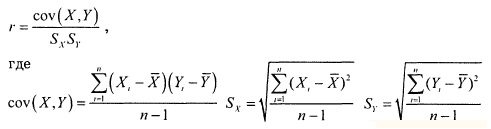
не нашли ответа на свои вопросы