В настоящей заметке χ2-распределение используется для проверки согласованности набора данных с фиксированным распределением вероятностей. В критерии согласия частоты, принадлежащие определенной категории, сравниваются с частотами, которые являются теоретически ожидаемыми, если бы данные действительно имели указанное распределение. [1]
Проверка с помощью критерия согласия χ2 выполняется в несколько этапов. Во-первых, определяется конкретное распределение вероятностей, которое сравнивается с исходными данными. Во-вторых, выдвигается гипотеза о параметрах выбранного распределения вероятностей (например, о ее математическом ожидании) или проводится их оценка. В-третьих, на основе теоретического распределения определяется теоретическая вероятность, соответствующая каждой категории. В заключение, для проверки согласованности данных и распределения применяется тестовая χ2-статистика:
где f0 — наблюдаемая частота, fе — теоретическая, или ожидаемая частота, k — количество категорий, оставшихся после объединения, р — количество оцениваемых параметров.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Использование χ2-критерия согласия для распределения Пуассона
Ранее распределение Пуассона использовалось для моделирования количества клиентов, прибывающих в отделение банка в течение минуты. Предположим, что в течение недели фактическое количество клиентов, приходящих в отделение банка в течение минуты, измерялось 200 раз (рис. 1).
Рис. 1. Распределение частоты прибытий в минуту во время ланча
Для того чтобы определить, имеет ли количество прибытий в минуту распределение Пуассона, формулируются нулевая и альтернативная гипотеза. Н0: количество прибытий в минуту подчиняется распределению Пуассона, Н1: количество прибытий в минуту не подчиняется распределению Пуассона. Поскольку распределение Пуассона имеет один параметр — математическое ожидание λ, в нулевую и альтернативную гипотезы можно включать либо величину λ, либо ее выборочную оценку. В нашем примере для оценки среднего количества прибытий клиентов необходимо воспользоваться формулой (подробнее об этой формуле см. Описательные статистики):
Для расчета по этой формуле в Excel удобно воспользоваться функцией =СУММПРОИЗВ() (рис. 1).
Для оценки параметра λ можно воспользоваться оценкой ![]() . Теоретическую частоту X успехов (Х = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и более), соответствующую параметру λ = 2,9 можно определить с помощью функции =ПУАССОН.РАСП(Х;
. Теоретическую частоту X успехов (Х = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и более), соответствующую параметру λ = 2,9 можно определить с помощью функции =ПУАССОН.РАСП(Х;![]() ;ЛОЖЬ). Умножив пуассоновскую вероятность на объем выборки n, получим теоретическую частоту fe (рис. 2).
;ЛОЖЬ). Умножив пуассоновскую вероятность на объем выборки n, получим теоретическую частоту fe (рис. 2).
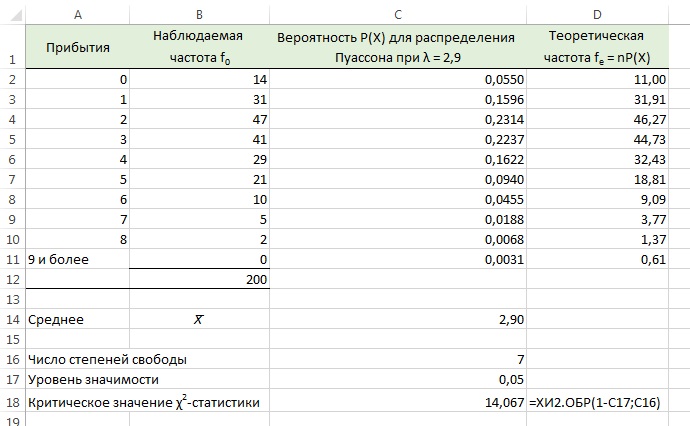
Рис. 2. Фактические и теоретические частоты прибытий в минуту
Как следует из рис. 2, теоретическая частота девяти и более прибытий не превосходит 1,0. Для того чтобы каждая категория содержала частоту, равную 1,0 или большему числу, категорию «9 и более» следует объединить с категорией «8». То есть, остается девять категорий (0, 1, 2, 3, 4, 5, 6, 7, 8 и более). Поскольку математическое ожидание распределения Пуассона определяется на основе выборочных данных, количество степеней свободы равно k – р – 1 = 9 – 1 – 1 = 7. Используя уровень значимости, равный 0,05 находим критическое значение χ2-статистики, имеющей 7 степеней свободы по формуле =ХИ2.ОБР(1-0,05;7) = 14,067. Решающее правило формулируется следующим образом: гипотеза Н0 отклоняется, если χ2 > 14,067, в противном случае гипотеза Н0 не отклоняется.
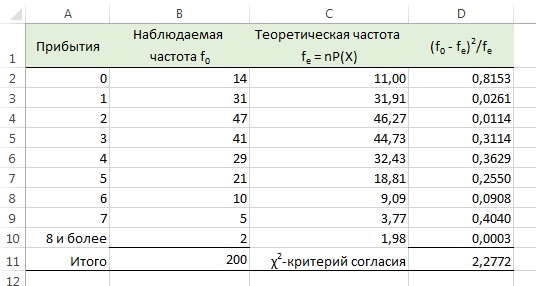
Для расчета χ2 воспользуемся формулой (1) (рис. 3).
Рис. 3. Расчет χ2-критерия согласия для распределения Пуассона
Так как χ2 = 2,277 < 14,067, следует, что гипотезу Н0 отклонять нельзя. Иначе говоря, у нас нет оснований утверждать, что прибытие клиентов в банк не подчиняется распределению Пуассона.
Применение χ2-критерия согласия для нормального распределения
В предыдущих заметках при проверке гипотез о числовых переменных использовалось предположение о том, что исследуемая генеральная совокупность имеет нормальное распределение. Для проверки этого предположения можно применять графические средства, например, блочную диаграмму или график нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). При больших объемах выборок для проверки этих предположений можно использовать χ2-критерий согласия для нормального распределения.
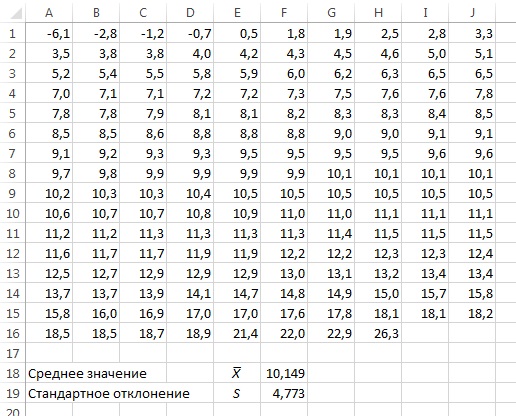
Рассмотрим в качестве примера данные о 5-летней доходности 158 инвестиционных фондов (рис. 4). Предположим, требуется поверить, имеют ли эти данные нормальное распределение. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: 5-летняя доходность подчиняется нормальному распределению, Н1: 5-летняя доходность не подчиняется нормальному распределению. Нормальное распределение имеет два параметра — математическое ожидание μ и стандартное отклонение σ, которые можно оценить на основе выборочных данных. В данном случае ![]() = 10,149 и S = 4,773.
= 10,149 и S = 4,773.
Рис. 4. Упорядоченный массив, содержащий данные о пятилетней среднегодовой доходности 158 фондов
Данные о доходности фондов можно сгруппировать, разбив, например на классы (интервалы) шириной 5% (рис. 5).
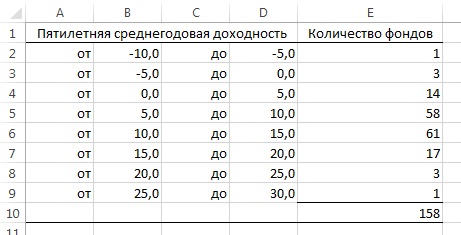
Рис. 5. Распределение частот для пятилетней среднегодовой доходности 158 фондов
Поскольку нормальное распределение является непрерывным, необходимо определить площадь фигур, ограниченных кривой нормального распределения и границами каждого интервала. Кроме того, поскольку нормальное распределение теоретически изменяется от –∞ до +∞, необходимо учитывать площадь фигур, выходящих за пределы классов. Итак, площадь, лежащая под нормальной кривой слева от точки –10, равна площади фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z, равной
Z = (–10 – 10,149) / 4,773 = –4,22
Площадь фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z = –4,22 определяется по формуле =НОРМ.РАСП(-10;10,149;4,773;ИСТИНА) и приближенно равна 0,00001. Для того чтобы вычислить площадь фигуры, лежащей под нормальной кривой между точками –10 и –5, сначала необходимо вычислить площадь фигуры, лежащей слева от точки –5: =НОРМ.РАСП(-5;10,149;4,773;ИСТИНА) = 0,00075. Итак, площадь фигуры, лежащей под нормальной кривой между точками –10 и –5, равна 0,00075 – 0,00001 = 0,00074. Аналогично можно вычислить площадь фигуры, ограниченной границами каждого класса (рис. 6).
Рис. 6. Площади и ожидаемые частоты для каждого класса 5-летней доходности
Видно, что теоретические частоты в четырех крайних классах (два минимальных и два максимальных) меньше 1, поэтому проведем объединение классов, как показано на рис 7.
Рис. 7. Вычисления, связанные с применением χ2-критерия согласия для нормального распределения
Используем χ2-критерий согласия данных с нормальным распределением с помощью формулы (1). В нашем примере после объединения остаются шесть классов. Поскольку математическое ожидание и стандартное отклонение оцениваются на основе выборочных данных, количество степеней свободы равно k – p – 1 = 6 – 2 – 1 = 3. Используя уровень значимости, равный 0,05, находим, что критическое значение χ2-статистики, имеющее три степени свободы =ХИ2.ОБР(1-0,05;F3) = 7,815. Вычисления, связанные с применением χ2-критерия согласия, приведены на рис. 7.
Видно, что χ2-статистика = 3,964 < χU27,815, следовательно гипотезу Н0 отклонять нельзя. Иначе говоря, у нас нет оснований утверждать, что 5-летняя доходность инвестиционных фондов, ориентированных на быстрый рост, не подчиняется нормальному распределению.
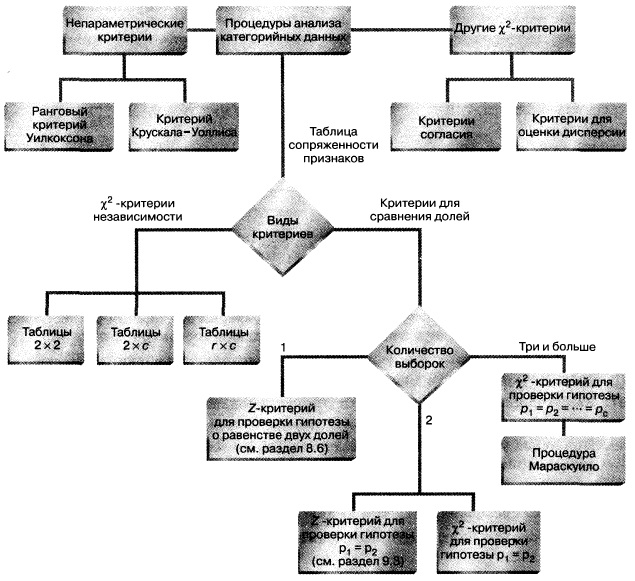
В нескольких последних заметках рассмотрены разные подходы к анализу категорийных данных. Описаны методы проверки гипотез о категорийных данных, полученных на основе анализа двух или нескольких независимых выборок. Кроме критериев «хи-квадрат», рассмотрены непараметрические процедуры. Описан ранговый критерий Уилкоксона, который используется в ситуациях, когда не выполняются условия применения t-критерия для поверки гипотезы о равенстве математических ожиданий двух независимых групп, а также критерий Крускала-Уоллиса, который является альтернативой однофакторному дисперсионному анализу (рис. 8).
Рис. 8. Структурная схема методов проверки гипотез о категорийных данных
Предыдущая заметка Критерий «хи-квадрат» для дисперсий
Следующая заметка Простая линейная регрессия
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 763–769


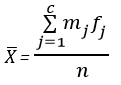


Здравствуйте! В расшифровке величин к формуле (1), наверное, ошибка. Вместо f1 — fe?
Ольга, спасибо. Поправил.
Здравствуйте, а можете рассказать, как работает критерий Пирсона для распределений с убывающей плотностью?