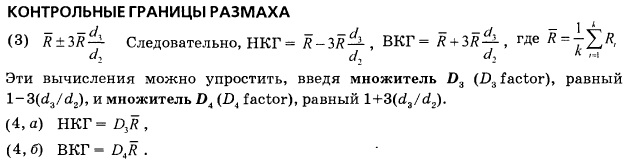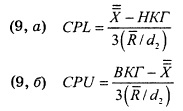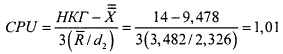В этой главе мы сосредоточимся на управлении качеством и производительностью труда. Компании, производящие товары и оказывающие услуги, понимают, что качество и производительность труда становятся жизненно важными в глобальной экономике. Начнем изучение методов управления качеством и производительностью труда с исторического обзора. Сформулируем 14 принципов Деминга, которые образуют основу для применения карт качества. Кроме того, изложим весьма поучительную притча о красных шарах, которая иллюстрирует изменчивость, присущую наборам данных, и подчеркивает ответственность менеджера за постоянное улучшение работы. [1]
Материал будет проиллюстрирован сквозным примером: управление качеством обслуживания в отеле Beachcomber. Поставьте себя на место управляющего отелем Beachcomber, прошедшего курс обучения методу Six Sigma. Стремясь улучшить качество обслуживания постояльцев, вы желаете произвести на них приятное первое впечатление. Существуют два важных фактора, характеризующих качество обслуживания — готовность комнат к приему гостей и скорость доставки багажа. Значит, в номерах должны быть все необходимые аксессуары (мыло, полотенца и т.п.). Не менее важно, чтобы в номерах исправно работали телевизор, радиоприемник и телефон. Кроме того, постояльцы, как правило, требуют, чтобы их багаж был доставлен в номер достаточно быстро. Для того чтобы удовлетворить потребности клиентов, администрация отеля должна собирать данные о степени готовности номеров и времени доставки багажа. Управляющий отелем должен постоянно анализировать эти данные и принимать необходимые решения. Например, вовремя ли доставляется багаж? Не изменяется ли время доставки багажа от случая к случаю? Если изменяется, то в какую сторону: увеличивается или уменьшается? Чем объясняются причины задержки — случайным стечением обстоятельств или серьезными недостатками в обслуживании? Если причины коренятся в плохой организации труда, необходимо принять экстренные меры, сократив время доставки багажа и улучшив качество обслуживания клиентов.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Тотальный контроль качества
В середине 1980-х годов стало ясно, что в условиях глобальной экономики компании вступают в конкуренцию не только с национальными производителями, но и с иностранными компаниями во всем мире. Глобализация экономики стала результатом стечения многих обстоятельств, в частности, быстрого роста средств коммуникации и доступности мощных компьютерных систем. В этой экономической среде чрезвычайно важно, чтобы организация бизнеса гибко реагировала на изменение рыночных условий и внедрение новых эффективных методов менеджмента.
Развитие глобальной экономики возродило интерес к повышению качества продукции в США. Свидетельством этого стало соревнование за приз Малкольма Балдриджа, который ежегодно присуждается компаниям, достигшим наивысших результатов в процессе улучшения качества своих товаров и услуг. К числу этих компаний относятся корпорации Motorola, Xerox, Federal Express, Cadillac Motor Company, Ritz-Carlton Hotels, AT&T Universal Card Services, Eastman Chemical Company и Los Alamos National Bank.
Принципы управления качеством были впервые сформулированы в 1950 году У. Демингом (подробнее см. У. Эдвардс Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами), Джозефом Джураном и Каору Ишикава, принимавшими участие в процессе возрождения экономики Японии. В основе этого подхода лежат методы улучшения качества и системной оптимизации. Системный подход к управлению часто называют тотальным контролем качества (total quality management — TQM). Он характеризуется следующими свойствами:
- Основное внимание уделяется улучшению процесса производства.
- Основной причиной изменчивости характеристик процесса являются особенности системы, а не случайные обстоятельства.
- Коллективная работа является неотъемлемой частью контроля качества.
- Основной целью организационных усилий является удовлетворение потребностей клиентов.
- Все организационные преобразования направлены на повышение качества работы.
- Из организации необходимо изгнать страх.
- Повышение качества требует затрат на обучение персонала.
Наибольшее влияние на развитие теории TQM оказал известный статистик У. Деминг. Подводя итоги своей работы в Японии и США, он сформулировал 14 основных принципов:
- Постоянно стремитесь к улучшению качества товаров и услуг.
- Овладевайте новым образом мышления.
- Не полагайтесь на контрольные проверки.
- Не ориентируйтесь на минимальную цену при закупке товаров. Вместо этого минимизируйте общие расходы, работая с одним поставщиком.
- Постоянно совершенствуйте планирование, производство и обслуживание.
- Обучение должно стать неотъемлемой частью работы.
- Поощряйте лидерство.
- Избавьтесь от страха.
- Устраните барьеры между подразделениями.
- Избегайте лозунгов, призывов и наставлений.
- Не устанавливайте количественные нормативы.
- Устраните барьеры, лишающие людей гордости за свою работу. Отмените ежегодный рейтинг и систему оценки работника по заслугам.
- Внедряйте интенсивную программу обучения и самосовершенствования каждого сотрудника.
- Вовлекайте каждого сотрудника в процесс преобразований.
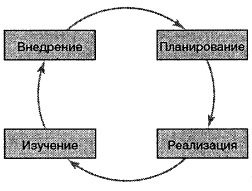
Первая рекомендация описывает процесс решения насущных и перспективных задач, стоящих перед организацией. Основное внимание уделяется постоянному улучшению качества продукции или услуг. Процесс улучшения качества продукции иллюстрируется циклом Шухарта-Деминга (рис. 1). Непрерывный цикл Шухарта-Деминга состоит из этапов планирования, реализации, изучения и внедрения. Планирование представляет собой первую фазу изменений производственного процесса. В него вовлекаются работники из разных подразделений организации. Второй этап — реализация — описывает процесс внедрения запланированных изменений, желательно в небольшом масштабе. Третий этап — изучение — сводится к анализу результатов с помощью статистических инструментов. Четвертый этап — внедрение — означает принятие или отклонение предложенных изменений, а также дальнейшее изучение последствий преобразований при разных условиях. Отличительной чертой этого процесса является ориентация на клиента, представляющего собой наиболее важный элемент производства или обслуживания.
Рис. 1. Цикл Шухарта-Деминга
Второй пункт, рекомендующий осваивать новый образ мышления, отражает необходимость осознания новых экономических реалий в условиях глобальной конкуренции. Лучше предугадать кризис, чем реагировать на его негативные последствия. Рекомендация отвергает принцип «не сломалось — не ремонтируй», а, напротив, понуждает постоянно работать над улучшением качества продукции и услуг, предупреждая дорогостоящий ремонт.
Третий пункт, призывающий не полагаться на контрольные проверки, основан на понимании того, что любые проверки, направленные на улучшение качества продукции, бессмысленны, поскольку проводятся слишком поздно — ведь продукция уже создана. Все нужно делать правильно с самого начала. Проверки качества порождают массу проблем — кроме высокой стоимости, они часто не позволяют отделить качественную продукцию от бракованной. Эти трудности иллюстрирует пример, описанный Шеркенбахом. Подсчитайте количество вхождений буквы F в предложении, приведенном на рис. 2.
Рис. 2. Проверка предложения
Как правило, люди обычно видят три или шесть вхождений буквы F. Правильный ответ— шесть букв. Количество обнаруженных вхождений зависит от метода, которым пользуются испытуемые. Скорее всего, читатели найдут три буквы F, если прочитают предложение вслух, и шесть — если тщательно пересчитают все буквы. Смысл этого примера заключается в том, что даже простейшая проверка может привести к неправильным результатам, что уж говорить о сложных процессах, протекающих в условиях неопределенности.
Четвертый пункт, рекомендующий отказаться от ориентации на цену товара, представляет собой полную противоположность подходу, в котором поощряются производители, предлагающие наиболее дешевый товар. Эта рекомендация означает, что в долговременной перспективе цена товара не может характеризовать его качество. Подход, в котором предпочтение отдается наиболее дешевой продукции, игнорирует преимущества, которые дает уменьшение колебаний цен в результате выбора одного поставщика, и не поощряет долговременные отношения между покупателем и поставщиком. Такие отношения стимулируют внедрение новшеств и делают покупателя и продавца партнерами, стремящимися к общему успеху.
Пятый пункт, подчеркивающий важность постоянного стремления к совершенствованию организации труда, ориентирует менеджеров на непрерывное улучшение процессов, описанных циклом Шухерта-Деминга. В основе этой рекомендации лежит твердое убеждение, что качество продукции закладывается уже на этапе планирования производства. Улучшение качества — бесконечный процесс, в котором уменьшение колебаний приводит к сокращению экономических потерь, являющихся следствием непостоянства характеристик продукции.
Шестой пункт, призывающий внедрять процесс обучения, касается всех сотрудников — начиная с рабочих и заканчивая инженерами и менеджерами. Руководство компании должно понимать разницу между случайными и неслучайными причинами отклонений (см. ниже). Это позволит адекватно реагировать на различные ситуации.
Пункты 8–12 рекомендуют руководителям избавиться от страха, устранить барьеры между подразделениями, избегать лозунгов, призывов и наставлений, не устанавливать количественные нормативы, устранить барьеры, лишающие людей гордости за свою работу (отменив ежегодный рейтинг и систему оценки работников по заслугам). Все эти рекомендации относятся к способам оценки производительности труда.
Тринадцатая рекомендация, призывающая заниматься образованием и самосовершенствованием, отражает общеизвестное мнение, что наиболее важным ресурсом любой компании являются ее сотрудники. Повышение квалификации персонала приводит к улучшению работы всей организации в целом.
Четырнадцатый пункт рекомендует вовлекать всех сотрудников в процесс улучшения производства. Он основан на убеждении, что процесс совершенствования бесконечен.
Весьма важным инструментом контроля качества являются карты контроля, позволяющие оценить изменчивость системы и принять правильное решение. Мы рассмотрим их далее.
Метод Six Sigma
Метод Six Sigma был изобретен компанией Motorola в середине 1980-х годов. Последние 10 лет он успешно используется компаниями General Electric и Allied Signal для сокращения затрат и повышения эффективности производства. Как и метод полного контроля качества, разработанный Демингом и другими исследователями, метод Six Sigma® использует статистику для выявления брака и уменьшения отклонений от нормы. Метод Six Sigma разбивает процесс на последовательные стадии. Он полностью исключает брак и приводит к практически идеальным результатам (см. также Концепция шести сигм, Джефф Кокс. Новая цель. Как объединить бережливое производство, шесть сигм и теорию ограничений, Пит Панде, Ларри Холп. Что такое «шесть сигм»? ).
Метод называется Six Sigma, потому что в результате его применения количество брака сокращается до 3,4 случаев на миллион единиц произведенной продукции. Отличительной чертой метода Six Sigma является стремление достичь итогового результата за период от трех до шести месяцев. Благодаря этому метод был горячо одобрен высшим руководством многих компаний. Модель, используемая в методе Six Sigma для улучшения производственных процессов, имеет пять компонентов: определение, измерение, анализ, улучшение и контроль (Define, Measure, Analyze, Improve and Control — DMAIC):
- Определение. Необходимо четко сформулировать поставленную задачу, определить затраты, возможную прибыль и воздействие на клиента.
- Измерение. Необходимо дать определение важнейших качественных характеристик. Кроме того, процедура измерения должна верифицироваться, чтобы все повторяющиеся измерения были непротиворечивы.
- Анализ. Необходимо обнаружить коренные причины брака, а также особенности производственного процесса, которые могут привести к браку. Данные, собранные для оценки производственных процессов, часто анализируются с помощью контрольных карт.
- Улучшение. С помощью спланированного эксперимента оценивается важность каждой изучаемой характеристики производственного процесса. Целью этого этапа является определение наилучшего уровня каждой характеристики, который можно поддерживать долгое время.
- Контроль. Цель этого этапа — долговременный контроль производственного процесса и предотвращение потенциальных проблем, которые могут возникнуть при изменении его характеристик.
Метод Six Sigma требует постоянного сбора и статистического анализа данных с помощью контрольных карт и спланированных экспериментов. Кроме того, необходимо обучить персонал. Как правило, на освоение этого метода уходит несколько месяцев.
Контрольные карты [2]
При сборе данных на протяжении определенного интервала времени необходимо изобразить график интересующей нас переменной. Одним из наиболее распространенных способов построения такого графика являются контрольные карты, предложенные Шухартом.
Контрольная карта позволяет следить за колебаниями качества продукции и услуг с течением времени, а также выявлять причину этой изменчивости. Ее можно использовать как для ретроспективного анализа эффективности работы, так и для оценки текущего положения дел. Данные, на основе которых строятся контрольные карты, образуют фундамент для улучшения системы. Контрольные карты используются для разнообразных переменных — категорийных, например, для доли номеров отеля, не соответствующих установленным нормам, дискретных, например, для количества постояльцев отеля, зарегистрированных в течение недели, и непрерывных, например, для времени, затраченного на доставку багажа. Кроме того, для облегчения анализа данных контрольная карта предусматривает средства, позволяющие отделить случайные вариации от неслучайных.
Неслучайные вариации представляют собой крупномасштабные или закономерные колебания данных, несвойственные процессу. Эти колебания часто объясняются изменениями самой системы, которые следует либо устранить, либо использовать. Случайная вариация представляет собой колебание, присущее процессу. Она является результатом действия многих незначительных и случайных причин.
Различие между случайными и неслучайными вариациями является принципиальным. Неслучайные вариации не являются частью процесса, поэтому их можно устранить или использовать, не изменяя саму систему. В то же время случайные вариации изначально присущи процессу и не могут быть ликвидированы без изменения системы. Систематические изменения, направленные на устранение случайных вариаций качества продукции, относятся к компетенции руководства компании.
Контрольные карты позволяют осуществлять мониторинг процесса и определять существование неслучайных вариаций. Это позволяет предотвратить ошибки двух видов. Ошибка первого типа возникает, когда исследователь считает, будто вариация является неслучайной, в то время как она имеет случайный характер. Это приводит к ненужной перестройке организации производства, что в результате вызывает еще большие отклонения. Ошибка второго типа возникает, когда исследователь считает случайную вариацию неслучайной и не вносит в производство необходимых корректив. Контрольные карты значительно снижают вероятность таких ошибок, хотя и не исключают их полностью.
Наиболее типичная разновидность контрольных карт устанавливает контрольные границы, находящиеся на расстоянии трех стандартных отклонений от среднего значения интересующей нас величины. Напомним, что для случайной величины, имеющей нормальное распределение, в интервале μ ± Зσ находится 99,73% наблюдений.
(1) Контрольные границы: Среднее значение ± 3 стандартных отклонения
Карта контроля показывает, находятся ли наблюдаемые величины внутри контрольных границ (рис.
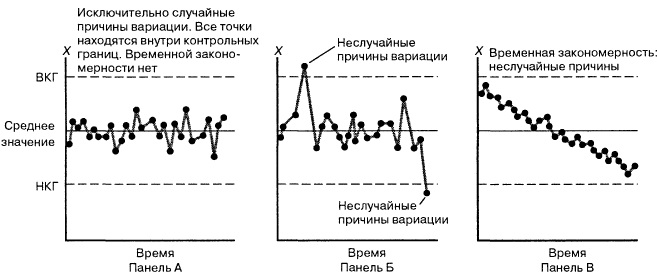
Рис. 3. Примеры карт контроля
На панели А в распределении величин не наблюдается никакой зависимости и все точки лежат внутри контрольных границ. Следовательно, процесс является устойчивым и подвержен лишь случайным вариациям. Панель Б представляет собой полную противоположность панели А. На ней две точки выходят за контрольные границы, что может свидетельствовать о существовании неслучайных причин вариации. Несмотря на то что на панели В все точки графика находятся внутри контрольных границ, и количество точек, расположенных над средним значением и под ним, приблизительно одинаково, график демонстрирует долговременный убывающий тренд. Эта ситуация требует энергичного вмешательства. Прежде чем приступать к изменениям системы, необходимо определить причины наблюдаемого явления.
Обнаружить тренд не всегда просто. Были сформулированы два простых правила, позволяющих распознать тренд: данные содержат тренд, если восемь последовательных точек лежат выше (ниже) средней линии или восемь последовательных точек расположены в убывающем (возрастающем) порядке.
Процесс, карта контроля которого свидетельствует о нарушениях границ контроля (точки лежат вне контрольных границ или образуют тренд), называется неконтролируемым. Неконтролируемый процесс имеет как случайные, так и неслучайные вариации. Поскольку неслучайные причины вариации являются внешними по отношению к процессу, неконтролируемые процессы невозможно предсказать. Когда процесс выходит из-под контроля, необходимо идентифицировать неслучайные причины. Если они отрицательно влияют на качество продукции или услуг, следует разработать мероприятия, направленные на их ликвидацию. Если же неслучайные причины повышают качество, их нужно использовать как составную часть процесса. В этой ситуации неслучайная причина становится источником случайных вариаций, а эффективность процесса повышается.
Процесс, контрольная карта которого не выявляет нарушений контрольных границ, называется контролируемым. Контролируемый процесс имеет только случайные вариации. Поскольку случайные вариации изначально присущи процессу, его можно прогнозировать. Иногда контролируемые процессы называются процессами, поддающимися статистическому контролю. Если процесс является контролируемым, необходимо определить величину случайной вариации. Требуется, чтобы она была невелика. Если величина случайной вариации достаточно мала, контрольную карту можно использовать для постоянного мониторинга процесса. В противном случае необходимо изменить сам процесс.
Процентные контрольные карты
Для мониторинга процесса и выявления неслучайных и случайных вариаций применяются различные типы контрольных карт, в частности, карты контроля качественных признаков. Эти карты используются в ситуациях, когда единицы продукции разделены на бракованные и качественные. Рассмотрим р-карты, показывающие долю бракованных изделий в выборке. Напомним, что выборочная доля р = Х/n (где Х – значение случайной величины, n – объем выборки), а стандартное отклонение пропорции вычисляется по формуле: . Используя формулу (1), можно вычислить контрольные границы для бракованных изделий:
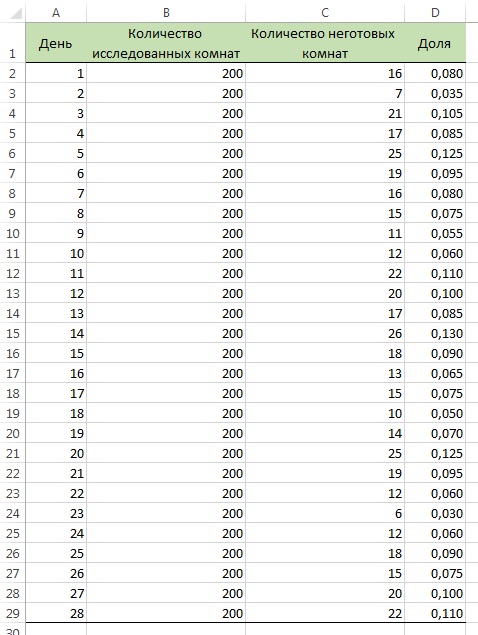
Отрицательное значение нижней контрольной границы означает, что ее вообще не существует. В качестве иллюстрации рассмотрим сценарий, изложенный в начале заметки. Чтобы применить р-карту для изучения готовности номеров в течение четырех недель, администрация отеля ежедневно формировала подгруппы, состоящие из 200 номеров. По методу Six Sigma на этапе измерения для каждого номера, входящего в выборку, определялась степень его готовности к приезду гостей. На этапе анализа количество номеров и доля комнат, не готовых к приезду гостей, были занесены в таблицу (рис. 4).
Рис. 4. Количество номеров и доля комнат, не готовых к приему гостей
Поскольку все величины ni равны, получаем:
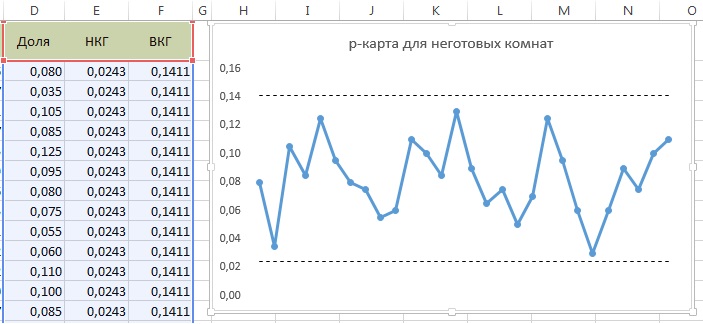
На рис. 5 показана карта контроля, соответствующая данным рис. 4. Анализ этой карты показывает, что процесс поддается статистическому контролю, все точки распределены вокруг значения р без какой бы то ни было закономерности и находятся внутри контрольных границ. Таким образом, на этапе контроля любое улучшение процесса подготовки комнат к приему гостей должно сопровождаться уменьшением случайных колебаний. Как указано выше, управление этим процессом находится в компетенции руководства компании. Помните: улучшения не наступят, пока весь процесс не будет успешно перестроен.
Рис. 5. Контрольная р-карта для неготовых номеров отеля; о методике построения подобных карт см. подробнее Пример построения контрольной карты Шухарта в Excel
В данном примере объемы подгрупп оставались постоянными, однако, как правило, со временем они изменяются. Если отклонение объемов подгрупп ni от среднего значения n̅ не превышает 25%, для вычисления контрольных границ применяется формула (2). Если же отклонение объемов подгрупп превышает указанный предел, используются альтернативные формулы.
Эксперимент с красными шарами: вариация процесса
В начале заметки были рассмотрены 14 принципов Деминга, метод Six Sigma, а также описаны случайные и неслучайные причины вариации. Для иллюстрации карт контроля мы изучили р-карты. Теперь перейдем к исследованию двух типов вариации — случайной и неслучайной. В качестве примера, демонстрирующего их сущность, рассмотрим знаменитый эксперимент Деминга с красными шарами.
В ходе эксперимента шары извлекаются из урны, содержащей 4000 шаров. Испытуемый не знает, что в урне 3200 (80%) белых шаров и 800 (20%) красных. Существует несколько сценариев эксперимента. Один из них начинается с того, что экспериментатор, играющий роль бригадира, приглашает не менее четырех добровольцев на роль рабочих. Затем бригадир приглашает добровольцев на роли контролеров (два человека), главного контролера (один человек) и регистратора (один человек). Рабочий должен погрузить в урну решето, состоящее из пяти рядов, образованных десятью отверстиями. Таким образом, рабочий может извлечь из урны 50 шаров.
Пригласив добровольцев, бригадир разъясняет им их обязанности. Рабочий должен отбирать только белые шары, красные считаются бракованными. Стандарты качества для рабочих весьма строги — рабочий должен извлечь 50 белых шаров, ни больше ни меньше. Кроме того, руководство установило, что каждый рабочий не должен извлекать более 2 красных шаров (4% брака). После того как решето погружается в урну, из нее извлекаются 50 шаров. Затем решето передается двум контролерам. Каждый из них независимо от другого записывает количество красных шаров. После этого главный контролер сравнивает результаты проверки и объявляет аудитории окончательный результат. Регистратор записывает количество и долю красных шаров, извлеченных каждым рабочим.
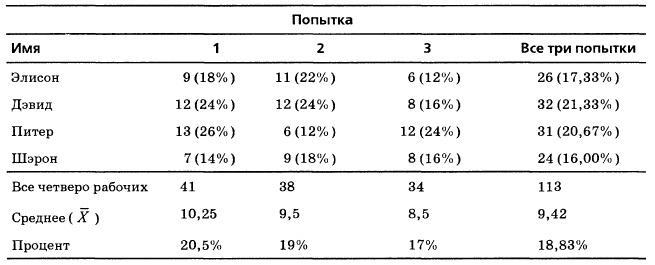
Уяснив свои обязанности, рабочие приступают к «работе». Предположим, что в первой попытке количество шаров, извлеченных каждым рабочим (назовем их Элисон, Дэвид, Питер и Шэрон), равно 9, 12, 13 и 7. Как руководство «компании» должно реагировать на эти результаты, учитывая, что допускаются не более двух красных шаров? Следует ли сделать выговор всем рабочим, или предупреждения должны получить только Дэвид и Питер? Предположим, что эксперимент состоит из трех попыток (рис. 6).
Рис. 6. Результаты трех попыток, выполненных четырьмя рабочими
В каждой попытке результат некоторых рабочих был выше среднего, а других — ниже среднего. В первой попытке лучшей была Шэрон, а во второй — Питер (при том, что в первой попытке он имел наихудший результат). В третьей попытке лучшей оказалась Элисон. Как объяснить все эти вариации? Ответ дает формула (2), выведенная для р-карт:
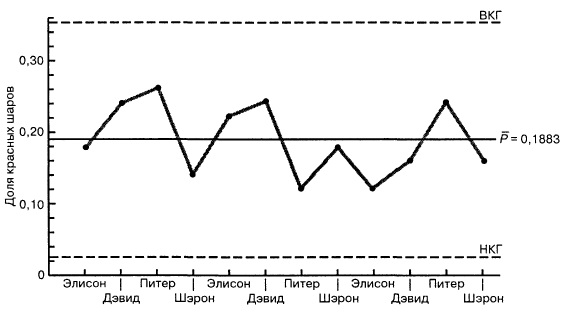
На рис. 7 приведена контрольная р-карта, построенная на основе данных рис. 6. Как видим, все точки лежат в пределах контрольных границ и не содержат каких-либо закономерностей. Разница в качестве работы сотрудников объясняется случайными причинами, присущими самой системе.
Рис. 7. Контрольная р-карта для эксперимента с красными шарами
Выводы из эксперимента с красными шарами:
- Вариация представляет собой неотъемлемую часть производственного процесса.
- Сотрудники работают внутри слабо управляемой системы. Результаты их работы определяются самой системой и от рабочих не зависят.
- Изменить систему может только руководство.
- Всегда существуют рабочие, результаты которых превышают среднее значение, и рабочие, качество труда которых ниже среднего.
Контрольные карты для размаха и среднего значения
Если исследователя интересуют числовые характеристики, для мониторинга можно использовать карты контроля переменных. Поскольку числовые характеристики более информативны, чем доля или количество бракованных изделий, карты контроля переменных более чувствительны к случайным вариациям. Такие контрольные карты обычно применяются попарно. Одна карта используется для мониторинга вариации процесса, а вторая — для контроля за его средним значением. Первая карта должна анализироваться в первую очередь, поскольку именно она позволяет определить, не вышел ли процесс из-под контроля. Карта среднего значения для этой цели не подходит. Если необходимо исследовать как среднее значение, так и размах процесса, используются несколько карт контроля.
Контрольная карта для размаха: R-карта. Прежде чем вычислять контрольные границы для среднего значения, необходимо построить карту контроля размаха, или R-карту. Это позволит определить, контролируема ли вариация процесса и нет ли сдвига результатов по времени. Если процесс является контролируемым, эту карту можно использовать при построении карты контроля для среднего значения.
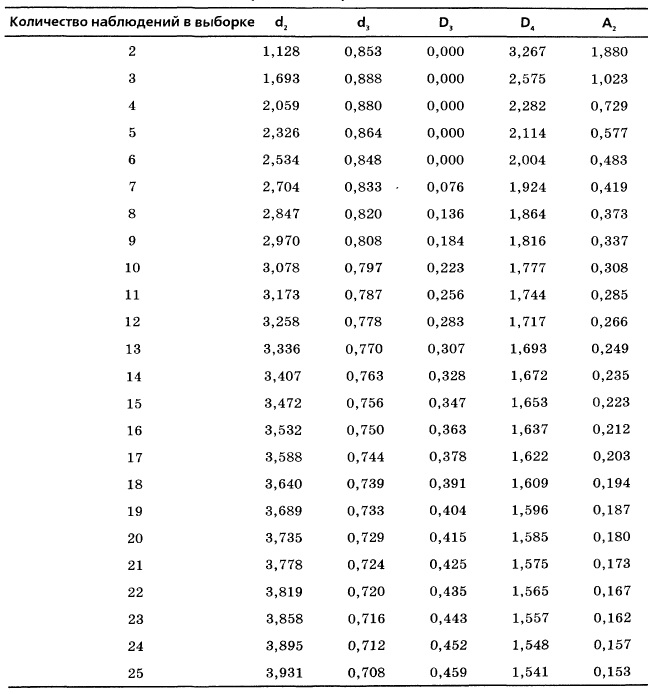
Из формулы (1) следует, что при построении контрольной карты необходимо получить оценку среднего размаха и стандартное отклонение размаха. Формула (4) показывает, что контрольные границы зависят от двух переменных — множителя d2, описывающего отношение между стандартным отклонением и размахом при переменном объеме выборки, и множителя d3, описывающего отношение между стандартным отклонением и стандартной ошибкой размаха при переменном объеме выборки (рис.8).
Рис. 8. Множители контрольных карт
Контрольные границы для размаха k соседних последовательностей или периодов вычисляются по формулам:
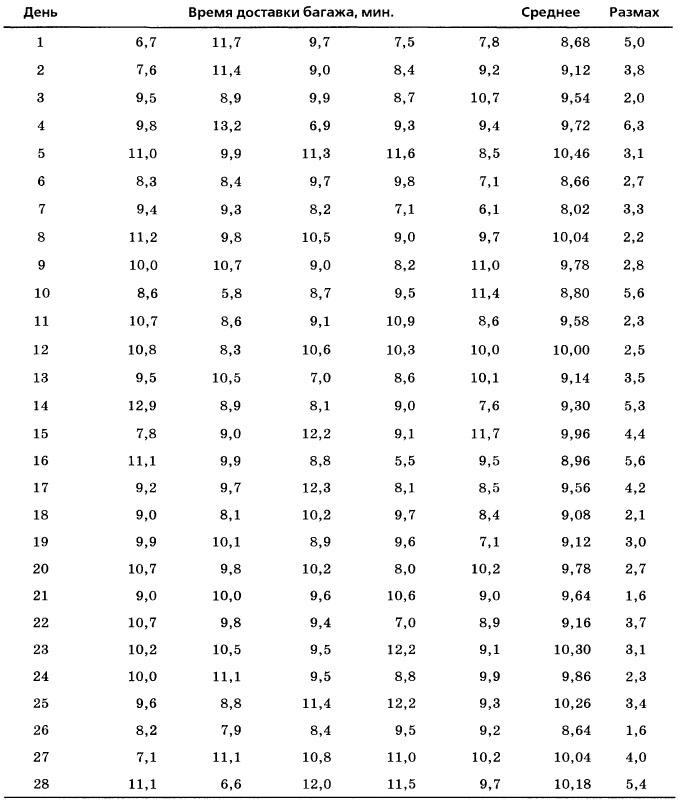
Вернемся к сценарию, описанному в начале заметки. Для того чтобы оценить качество обслуживания, менеджер отеля на протяжении четырех недель записывал время, затрачиваемое на доставку багажа (от регистрации до вручения). Для контроля были отобраны подгруппы, состоящие из пяти курьеров, работавших в вечернюю смену (рис. 9).
Рис. 9. Средние значения и размах времени доставки для каждой из подгрупп
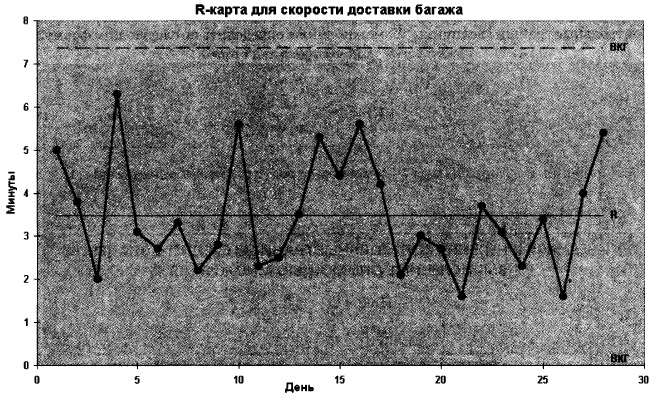
Обратите внимание на то, что нижняя контрольная граница для R не существует, поскольку размах не может быть отрицательным (рис. 10). Видно, что все точки находятся внутри контрольных границ.
Рис. 10. Контрольная карта размаха (R-карта), построенная для оценки времени доставки багажа
Контрольная ![]() -карта. Рассмотрим карту контроля среднего значения процесса, так называемую
-карта. Рассмотрим карту контроля среднего значения процесса, так называемую ![]() -карту. Карта контроля для величины
-карту. Карта контроля для величины ![]() использует подгруппы одинакового объема n, полученные в течение k последовательных периодов времени. Из формулы (1) следует, что при вычислении контрольных границ для среднего значения необходимо оценить средние значения в каждой из подгрупп
использует подгруппы одинакового объема n, полученные в течение k последовательных периодов времени. Из формулы (1) следует, что при вычислении контрольных границ для среднего значения необходимо оценить средние значения в каждой из подгрупп ![]() и стандартное отклонение среднего
и стандартное отклонение среднего ![]() . Эти контрольные границы являются функциями множителя d2, описывающего отношение между стандартным отклонением и размахом при переменном объеме выборки. В качестве оценки стандартного отклонения генеральной совокупности используется величина
. Эти контрольные границы являются функциями множителя d2, описывающего отношение между стандартным отклонением и размахом при переменном объеме выборки. В качестве оценки стандартного отклонения генеральной совокупности используется величина ![]() , а в качестве оценки стандартного отклонения среднего — величина
, а в качестве оценки стандартного отклонения среднего — величина ![]()
Контрольные границы среднего значения:
Возвращаясь к сценарию, изложенному в начале заметки, получаем:
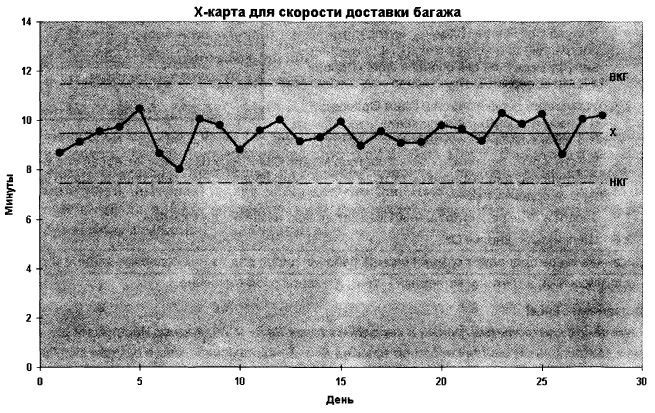
Результаты совпадают с точностью до ошибки округления. Анализ рис. 11 показывает, что все точки находятся внутри контрольных границ, причем никакого тренда не существует, хотя в 28-й день наблюдалась сильное колебание средних значений. Поскольку R— и X̅-карты показывают, что процесс находится под контролем, колебание времени доставки багажа объясняется случайными причинами. Если руководство отеля решит сократить время доставки багажа, оно должно изменить сам процесс.
Рис. 11. Контрольная ![]() -карта для оценки времени доставки багажа
-карта для оценки времени доставки багажа
Характеристики процесса
Иногда возникает необходимость оценить величину случайных вариаций, возникающих в контролируемом процессе. В частности, требуется знать, достаточно ли мала величина случайных вариаций, чтобы удовлетворить большинство потребителей. Если случайная вариация слишком велика, многие клиенты могут быть недовольны качеством продукции, т.е. процесс необходимо изменить. Для того чтобы ответить на эти вопросы, следует проанализировать характеристики процесса. Существует много методов анализа характеристик производственного процесса. Начнем с относительно простого способа, основанного на оценке процента качественных изделий.
Удовлетворение клиентов и допускаемые пределы. Качество определяется потребителем. Если клиент считает, что изделие или услуга соответствуют его ожиданиям, он остается удовлетворенным. Руководство компании должно прислушиваться к пожеланиям клиентов и устанавливать допустимые пределы колебания характеристик продукции. Допускаемые пределы — это технические характеристики продукции, устанавливаемые руководством компании в соответствии с пожеланиями клиентов. Верхняя контрольная граница (ВКГ) — наибольшее допустимое значение характеристики продукции. Нижняя контрольная граница (НКГ) — наименьшее допустимое значение характеристики продукции.
Например, производители мыла должны понимать, что клиенты ожидают от мыла определенного количества пены. Потребители будут разочарованы, если мыло будет мылиться либо слишком сильно, либо слишком слабо. Специалисты знают, что количество пены зависит от уровня свободных жирных кислот. Следовательно, менеджер должен установить верхнюю и нижнюю контрольные границы концентрации свободных жирных кислот, содержащихся в мыле. Сценарий, изложенный в начале заметки, представляет собой пример процесса, для которого установлена лишь одна допустимая граница. Поскольку постояльцы желают, чтобы их багаж был доставлен как можно быстрее, менеджеры отеля должны установить лишь верхнюю контрольную границу. Как видим, в обоих случаях допустимая граница зависит от пожеланий клиентов. Если процесс полностью соответствует их требованиям, он называется удовлетворительным.
Мощность процесса (process capability) — это способность процесса удовлетворять потребности клиентов. Для того чтобы оценить мощность процесса, можно оценить процент изделий или услуг, удовлетворяющих требованиям клиентов. В этом случае процесс должен быть контролируемым, поскольку предсказать мощность неконтролируемого процесса невозможно. Перед тем как приступить к анализу потенциала неконтролируемого процесса, необходимо установить и устранить причину неслучайной вариации. Любой неконтролируемый процесс считается неудовлетворительным и, следовательно, не может соответствовать ожиданиям клиентов. Для того чтобы оценить количество изделий, соответствующих установленным спецификациям, следует вычислить среднее значение и стандартное отклонение всех изделий или услуг. Оценка математического ожидания генеральной совокупности обозначается как ![]() . Она представляет собой среднее значение всех выборочных средних в формуле (5). Стандартное отклонение генеральной совокупности равно величине
. Она представляет собой среднее значение всех выборочных средних в формуле (5). Стандартное отклонение генеральной совокупности равно величине ![]() , деленной на число d2. Величины
, деленной на число d2. Величины ![]() и
и ![]() вычисляются по контрольным
вычисляются по контрольным ![]() — и R-картам, а число d2 можно найти в таблице (рис. 8). Допустим, что процесс является контролируемым, а величины X имеют нормальное распределение. Оценить вероятность того, что процесс выйдет за пределы допустимых границ, можно по формулам (7).
— и R-картам, а число d2 можно найти в таблице (рис. 8). Допустим, что процесс является контролируемым, а величины X имеют нормальное распределение. Оценить вероятность того, что процесс выйдет за пределы допустимых границ, можно по формулам (7).
Выше мы выяснили, что процесс доставки багажа является контролируемым. Предположим, что руководство отеля постановило, что 99% багажа должно доставляться за время, не превышающее 14 мин. Вычисления показывают, что
Вероятность Р(Z<3,02) =НОРМ.СТ.РАСП(3,02;ИСТИНА) = 0,99874. Итак, вероятность того, что багаж будет доставлен вовремя, равна 99,874%. Следовательно, процесс доставки багажа удовлетворяет требованиям руководства отеля.
Показатели мощности. Для оценки процесса можно воспользоваться показателем мощности — суммарным показателем, характеризующим соответствие процесса установленным спецификациям. Чем выше этот показатель, тем лучше. Чаще всего показатель качества обозначают символом Ср и вычисляют по формуле:
Числитель в этой формуле представляет собой расстояние между верхней и нижней контрольными границами, или размах спецификации. Знаменатель равен шести стандартным отклонениям данных и называется разброс процесса. (Напомним, что 99,73% всех нормально распределенных случайных величин лежит в интервале, концы которого отстоят на три стандартных отклонения от среднего значения.) Поскольку идеальный процесс должен полностью лежать в допустимом диапазоне, разброс процесса должен быть как можно меньше. Следовательно, чем больше значение Ср, тем выше качество процесса.
Величина Ср оценивает потенциал процесса, а не фактическую мощность, поскольку он не зависит от текущего среднего значения. Допустим, что Ср = 1. Тогда, если процесс является центрированным, т.е. лежит посередине между границами НКГ и ВКГ, приблизительно 99,73% наблюдений попадут внутрь допустимых границ. Если Ср > 1, значит, потенциал процесса настолько высок, что более 99,73% всех его значений может лежать внутри допустимых границ. Если Ср < 1, значит, потенциал процесса невысок, и даже если он идеально центрирован, не более 99,73% всех его значений может лежать внутри допустимых границ. Многие компании требуют, чтобы величина Ср была больше или равна единице. По мере развития глобальной экономики, требующей повышения качества продукции, некоторые компании стали требовать, чтобы показатель Ср превышал 1,33, 1,5 и даже 2,0 (Six Sigma).
Предположим, что компания, выпускающая безалкогольные напитки, разливает лимонад в 12-унциевые бутылки. Каждый час контролер извлекает одну бутылку, а затем вычисляет среднее значение и размах процесса. Нижняя допустимая граница равна 11,82 унции, а верхняя— 12,18 унций. Допустим, карта контроля показывает, что процесс находится под контролем, причем n = 4, ![]() = 12,02,
= 12,02, ![]() = 0,10. Для того чтобы вычислить показатель Ср, предположим, что данные имеют нормальное распределение. По таблице (рис.8) для n = 4 находим, что d2 = 2,059. Используя формулу (8), получаем:
= 0,10. Для того чтобы вычислить показатель Ср, предположим, что данные имеют нормальное распределение. По таблице (рис.8) для n = 4 находим, что d2 = 2,059. Используя формулу (8), получаем:
Поскольку показатель Ср превышает единицу, процесс разлива безалкогольных напитков имеет высокий потенциал, причем более 99,73% бутылок могут удовлетворять установленным спецификациям.
Итак, показатель Ср представляет собой суммарную меру потенциала процесса. Чем выше показатель Ср, тем лучше для потребителя. Иначе говоря, чем выше показатель Ср, тем меньше количество случайных вариаций и тем лучше процесс соответствует спецификациям. Для того чтобы достичь максимального потенциала, процесс должен колебаться вокруг среднего значения допустимого диапазона.
Показатели CPL, CPU и Сpk. Для измерения фактического потенциала процесса часто применяют показатели CPL, CPU и Сpk:
Поскольку при вычислении показателей CPL и CPU используется фактическое среднее значение, они характеризуют реальные свойства процесса, в отличие от показателя Ср, оценивающего лишь потенциал процесса. Если величина CPL (или CPU) равна единице, значит, среднее значение процесса отстоит от нижней (верхней) допустимой границы на три стандартных отклонения. Если процесс имеет только нижнюю допустимую границу, показатель CPL измеряет характеристики процесса и должен быть как можно больше. Если процесс имеет только верхнюю допустимую границу, показатель CPU измеряет характеристики процесса и тоже должен быть как можно больше.
Руководство отеля Beachcomber в нашем сценарии постановило, что 99% багажа должно доставляться за время, не превышающее 14 мин. Следовательно, характеристики качества процесса ограничены сверху числом 14, а нижней границы не существует. Поскольку ранее мы показали, что процесс доставки багажа является контролируемым, остается определить показатель CPU. Вычисления показывают, что ![]() = 9,478,
= 9,478, ![]() = 3,482, d2 = 2,326. Таким образом,
= 3,482, d2 = 2,326. Таким образом,
Итак, показатель мощности процесса равен 1,01. Поскольку эта величина ненамного больше единицы, расстояние от верхней допустимой границы до среднего значения процесса слегка отличается от трех стандартных отклонений. Следовательно, необходимо изучить процесс доставки багажа и увеличить показатель CPU.
Наиболее распространенным показателем качества процесса является величина Срk. Этот показатель измеряет фактическое качество процесса, имеющего нижнюю и верхнюю допустимые границы. Величина Срk представляет собой минимальное из двух показателей CPU и CPL:
(10) Срk = MIN[CPL,CPU]
Если величина Срk равна единице, значит, среднее значение процесса отстоит на три стандартных отклонения от ближайшей допустимой границы. Если к тому же характеристика является нормально распределенной, значит, 99,73% текущих результатов лежат в допустимом диапазоне. Как и для всех остальных показателей качества, чем больше величина Срk, тем лучше.
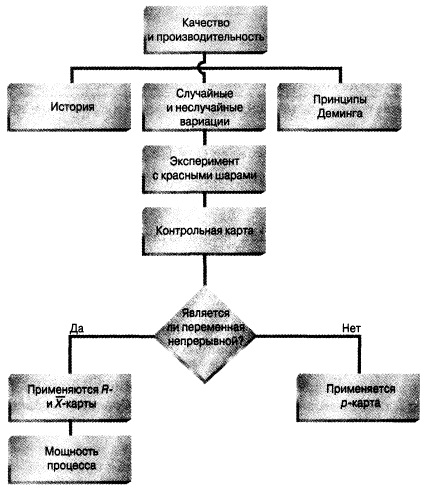
Резюме. В заметке рассмотрена теория контроля качества и принципы Деминга. Изучены различные типы карт контроля, позволяющие выделять случайные и неслучайные вариации. Кроме того, мы научились оценивать характеристики процесса, вычисляя процент качественной продукции и показатели мощности. В качестве иллюстрации рассмотрен сценарий, описывающий обслуживание постояльцев отеля Beachcomber. Показано, как выявлять проблемы и непрерывно улучшать качество обслуживания (рис. 12).
Рис. 12. Структурная схема заметки
Предыдущая заметка Принятие решений
Это последняя заметка из книги
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 1113–1168
[2] Подробнее см. замечательную книгу Д. Уилер, Д. Чамберс «Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта»