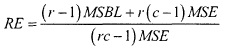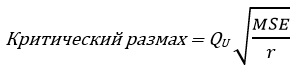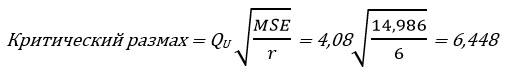Ранее был рассмотрен F-критерий однофакторного дисперсионного анализа для оценки разностей между математическими ожиданиями с групп. Этот критерий применяется в ситуациях, когда n однородных элементов (так называемых экспериментальных объектов) случайным образом распределяются по с уровням исследуемого фактора (так называемые группы условий факторного эксперимента. Такие эксперименты называются полностью рандомизированными. [1]
Кроме того, в заметке Проверка гипотез: двухвыборочные критерии был описан t-критерий для оценки разностей между математическими ожиданиями, который используется в ситуациях, связанных с повторяющимися измерениями или согласованными выборками. Этот критерий позволяет оценить различия между условиями проведения двух экспериментов. Предположим, что мы исследуем несколько групп условий или уровней исследуемого фактора. В таких ситуациях совокупности неоднородных объектов или индивидуумов, подлежащих сравнению (или повторным измерениям), называются блоками. Допустим, мы получили числовые результаты измерений для каждой группы условий и комбинаций блоков.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Эксперименты, в которых используются блоки, называются блочными рандомизированными экспериментами. Хотя в таких схемах используются как условия, так и блоки, основное внимание уделяется оценке разностей между с разными группами условий. Целью объединения условий в блоки является максимально возможное исключение изменчивости экспериментальной ошибки с тем, чтобы разности между с групп условий проявились как можно отчетливее. Блочные рандомизированные эксперименты часто оказываются более эффективными, чем полностью рандомизированные эксперименты и, следовательно, позволяют получать более точные результаты.
Для сравнения полностью рандомизированных и блочных рандомизированных экспериментов вспомним сценарий, посвященный компании Perfect Parachute Company («Идеальный парашют»), использованный в предыдущей заметке. Парашюты изготавливаются из синтетических волокон, поставляемых четырьмя разными поставщиками. На фабрике используется два вида ткацких станков: Jetta и Turk. Одной из основных характеристик парашюта является его прочность. Предположим, что в полностью рандомизированном эксперименте используются 12 наблюдений — по одному виду ткани на каждую из 12 смен. Любая изменчивость результатов испытаний становится частью экспериментальной ошибки, и, следовательно, различия между четырьмя поставщиками труднее уловить. Для того чтобы уменьшить экспериментальную ошибку, разработаем блочный рандомизированный эксперимент, в котором исследуются три смены, в течение каждой из которых ткутся четыре парашюта (один парашют — из волокон, полученных от первого поставщика, второй — из волокон, полученных от второго поставщика, и т.д.). Три смены рассматриваются как блоки, а условием факторного эксперимента является поставщик. Преимущество блочного рандомизированного эксперимента заключается в том, что из экспериментальной ошибки исключается изменчивость между тремя сменами. Следовательно, этот эксперимент часто обеспечивает более точные оценки различий между четырьмя поставщиками.
Критерии для оценки эффектов условий факторного эксперимента и блоков
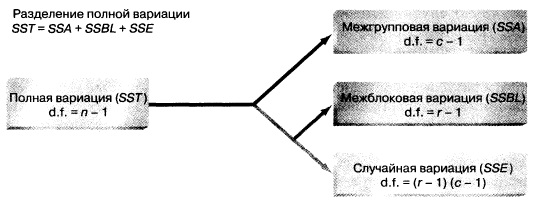
Напомним, что в полностью рандомизированном эксперименте полная вариация (SST) подразделяется на межгрупповую (SSA) и внутригрупповую (SSW). Внутригрупповая вариация считается экспериментальной ошибкой, а межгрупповая вариация возникает вследствие различий между условиями факторного эксперимента. Для того чтобы отделить эффект блокировки от экспериментальной ошибки блочного рандомизированного эксперимента, необходимо подразделить внутригрупповую вариацию на межблочную вариацию (SSBL) и случайную ошибку (SSE) (рис. 1). Следовательно, в блочном рандомизированном эксперименте полная вариация результатов измерений представляет собой сумму межгрупповой вариации (SSA), межблочной вариации (SSBL) и случайной ошибки (SSE).
Рис. 1. Разделение полной вариации в блочном рандомизированном эксперименте
Для того чтобы разработать процедуру дисперсионного анализа для блочного рандомизированного эксперимента, введем следующие обозначения: r — количество блоков, с — количество групп или уровней фактора, n — общее количество наблюдений (n = rс), Хij — величина в i-м блоке и j-группе, ![]() i — среднее всех величин из i-гo блока,
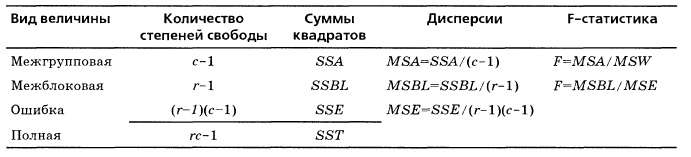
i — среднее всех величин из i-гo блока, ![]() j — среднее всех величин из j-й группы. Основные параметры блочного рандомизированного эксперимента представлены на рис. 2.
j — среднее всех величин из j-й группы. Основные параметры блочного рандомизированного эксперимента представлены на рис. 2.
Рис. 2. Сводная таблица дисперсионного анализа для блочного рандомизированного эксперимента
Проиллюстрируем блочный рандомизированный эксперимент следующим примером. Предположим, что сеть ресторанов быстрого питания, имеющая четыре подразделения в определенном географическом регионе, желает оценить качество обслуживания в этих ресторанах. Для этой цели директор нанял шесть экспертов, имеющих разный опыт. Чтобы уменьшить эффект вариации между экспертами, был разработан блочный рандомизированный эксперимент, в которых блоками считались эксперты. В свою очередь, четыре ресторана образовали группы условий факторного эксперимента. Шесть экспертов в случайном порядке инспектировали каждый из четырех ресторанов. Для оценки использовалась шкала баллов от 0 (низшая оценка) до 100 (рис. 3).
Рис. 3. Рейтинги четырех ресторанов быстрого питания
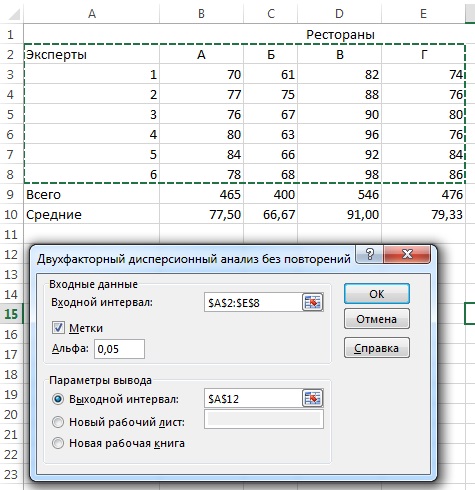
Как следует из рис. 3, r = 6, c = 4, n = rc = 24. Для проведения анализа пройдите по меню Данные → Анализ данных и в открывшемся окне выберите строку Двухфакторный дисперсионный анализ без повторений (рис. 4). Результаты анализа представлены на рис. 5.
Рис. 4. Использование Пакета анализа для блочного рандомизированного эксперимента
Рис. 5. Результаты инспекции сети ресторанов быстрого питания, полученные с помощью Пакета анализа Excel
Если установить уровень значимости критерия для проверки гипотезы о существовании различий между подразделениями сети ресторанов равным 0,05, решающее правило примет следующий вид: нулевая гипотеза Н0 (μ1 = μ2 = μ3 = μ4) отклоняется, если F > 3,287. Число 3,287 представляет собой верхнее критическое значение F-распределения, имеющего три степени свободы в числителе и 15 степеней свободы в знаменателе (строка Столбцы колонка F критическое таблицы Дисперсионный анализ на рис. 5). Поскольку F = 39,758 > FU = 3,29 (кроме того, р = 0,000 < 0,05), мы можем отклонить гипотезу Н0 и утверждать, что средние рейтинги ресторанов статистически значимо различаются между собой. Чрезвычайно малое значение р означает, что, если бы средние рейтинги четырех подразделений были одинаковыми, вероятность обнаружить разности между их выборочными средними, была бы крайне малой. Итак, нулевая гипотеза практически невероятна. Следовательно, альтернативную гипотезу можно считать корректной.
Для проверки эффективности блокировки, можно проверить разность между экспертами. При 5%-ном уровне значимости решающее правило можно сформулировать следующим образом: нулевая гипотеза Н0 (μ1 = μ2 = μ3 = μ4 = μ5 = μ6) отклоняется, если вычисленная статистика F > 2,901. Число 2,901 представляет собой верхнее критическое значение F-распределения, имеющего пять степеней свободы в числителе и 15 степеней свободы в знаменателе. Поскольку F = 3,782 > FU = 2,901 (а р = 0,02 < 0,05), мы может отклонить гипотезу Н0 и утверждать, что средние рейтинги ресторанов статистически значимо различаются между собой. Итак, применение блоков уменьшает экспериментальную ошибку.
Кроме обычных ограничений, принятых в однофакторном дисперсионном анализе, необходимо также предположить, что между условиями факторного эксперимента и блоками нет взаимодействия. Иначе говоря, необходимо, чтобы все различия между условиями эксперимента (ресторанами) были согласованы со всеми блоками (отмечались всеми экспертами). После разработки схемы блочного рандомизированного эксперимента и анализа данных о рейтингах ресторанов возникает вопрос: какой эффект оказывает блокирование на дисперсионный анализ? Иначе говоря, получаем ли мы более точные результаты, применяя блокирование при анализе разных групп условий факторного эксперимента? Для того чтобы ответить на этот вопрос, следует вычислить оценку относительной эффективности блочного рандомизированного эксперимента по сравнению с полностью рандомизированным экспериментом.
Оценка относительной эффективности
Подставляя наши данные, получаем
Это означает, что для получения такой же точности при сравнении средних по группам в рамках однофакторного дисперсионного анализа нам понадобилось бы в 1,6 раза увеличить количество наблюдений в каждой группе.
Множественные сравнения: процедура Тьюки
Как и в полностью рандомизированном эксперименте, отклонив нулевую гипотезу о равенстве всех средних по группам, мы можем определить, какая группа условий значительно отличается от остальных. Для блочного рандомизированного эксперимента такая процедура была разработана Джоном Тьюки. Критический размах в процедуре Тьюки вычисляется по формуле:
где статистика QU представляет собой верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и (r – 1)(с – 1) степеней свободы в знаменателе. К сожалению, для вычисления стьюдентизированного размаха нет функций в Excel (по крайней мере, я ее не нашел). Приходится пользоваться таблицами. Каждая из с(с – 1)/2 пар средних сравнивается с одним критическим размахом. Пара, например, группа j— группа j’ объявляется статистически значимо разными, если модуль разности между выборочными средними |Xj – Xj’| превышает критический размах.
Продемонстрируем применение процедуры Тьюки на примере анализа сети ресторанов. Поскольку проверке подвергаются четыре ресторана, в процедуре Тьюки будет выполнено 4(4 – 1)/2 = 6 попарных сравнений (рис. 6).
Рис. 6. Попарные сравнения средних значений по выборкам отдельных ресторанов
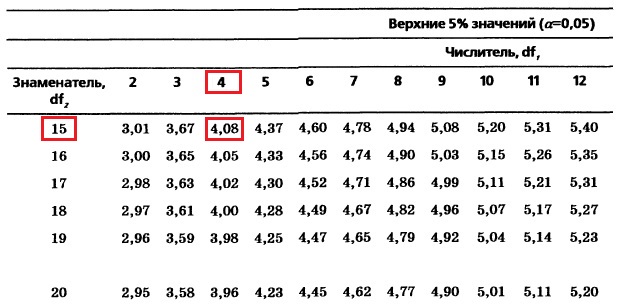
Для того чтобы вычислить критический размах, заметим (см. рис. 5): MSE = 14,986 и r = 6. Для α = 0,05, с = 4 и (r – 1)(с – 1) = 15 по таблице (рис. 7) находим, что величина QU — верхнее критическое значение тестовой статистики, имеющей четыре степени свободы в числителе и 15 степеней свободы в знаменателе— равна 4,08.
Рис. 7. Критическое значение стьюдентизированного размаха QU; к сожалению, в Excel нет функции, рассчитывающей такой размах
Таким образом:
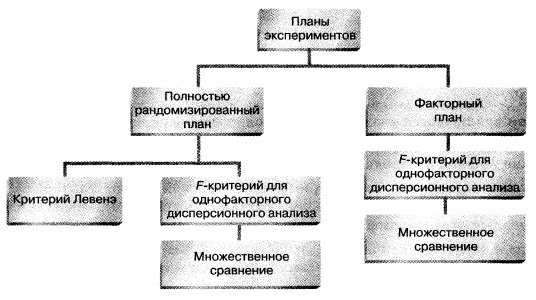
В этой и двух предыдущих заметках (см. Однофакторный дисперсионный анализ и Двухфакторный дисперсионный анализ) описана концепция полностью рандомизированного эксперимента. Приведены различные процедуры анализа эффекта одного и двух факторов. Рассмотрен практический пример, иллюстрирующий применение критериев одно- и двухфакторного дисперсионного анализа. Детально описаны условия выполнения статистических процедур. Напомним, что проверка необходимых условий является неотъемлемой частью статистического анализа и позволяет правильно выбирать критерии. Как показано на структурной схеме (рис. 8), существует несколько подходов к сравнению групп числовых данных на основе экспериментов.
Рис. 8. Структурная схема трех заметок по теме дисперсионного анализа
Предыдущая заметка Двухфакторный дисперсионный анализ
Следующая заметка Применение χ2-критерия для проверки гипотезы о равенстве двух или нескольких долей
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 681–693