Александр Орлов. О методах проверки однородности двух независимых выборок

В последнее время я изучаю решения менеджеров в Fantasy Premier League (FPL). В частности, есть ли отличия в поведении лучших менеджеров, отобранных по результатам предыдущих сезонов, и случайной выборкой. Важный аспект такого исследования – вынесение суждения, однородны ли выборки. Можно ли объяснить различия случайностью, или они закономерны? Ранее я рассказал о критерии Колмогорова и трудностях его использования. Настоящая статья Александра Ивановича Орлова дает современный обзор методов проверки однородности двух независимых выборок. По ходу изложения я применяю критерии к задаче FPL. Этот текст набран с отступом.

Александр Иванович Орлов. О методах проверки однородности двух независимых выборок. – Заводская лаборатория. Диагностика материалов. 2020. Том 86. № 3. Стр. 67–76.

Скачать заметку в формате Word или pdf, примеры в формате Excel

Оригинал статьи (для загрузки требуется авторизация).

Базовая вероятностно-статистическая модель

Постановка задачи в математико-статистических терминах: имеются две выборки x₁, x₂, …, x_m и y₁, y₂, …, y_n, требуется проверить их однородность. Понятием, противоположным однородности, является различие (или наличие эффекта). Можно переформулировать задачу: требуется проверить, есть ли различие между выборками.

При проверке однородности двух выборок общепринята модель, в которой x₁, x₂, …, x_m рассматриваются как результаты m независимых наблюдений некоторой случайной величины X с функцией распределения F(x), неизвестной статистику, а y₁, y₂, …, y_n – как результаты n независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Кроме того, предполагается, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.

В Fantasy Premier League сезона 2022/23 участвует более 10М аккаунтов. Я сформировал две выборки. Элита – ТОП-10К по рейтингу за пять предыдущих сезонов. Поляна – 10К, полученных с помощью генератора случайных чисел из первых 5М аккаунтов.

Основные постановки задачи проверки однородности двух независимых выборок

Однородность достигается, если обе выборки взяты из одной генеральной совокупности, т. е. справедлива нулевая гипотеза H₀: F(x) = G(x) при всех x. Отсутствие однородности означает, что верна альтернативная гипотеза H₁: F(x₀) ≠ G(x₀) хотя бы при одном значении аргумента x₀.

В некоторых случаях целесообразно проверять совпадение не функций распределения, а лишь некоторых характеристик случайных величин X и Y – математических ожиданий, медиан, дисперсий. Например, однородность математических ожиданий означает, что справедлива гипотеза H’₀: M(X) = M(Y), где M(X) и M(Y) – математические ожидания случайных величин X и Y.

Проверка однородности характеристик

Для проверки однородности математических ожиданий традиционно используют двухвыборочный критерий Стьюдента. К настоящему времени этот метод устарел, но по традиции встречается в учебной литературе. Сначала вычисляют выборочные средние арифметические

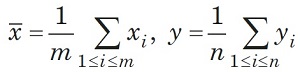
затем — выборочные дисперсии

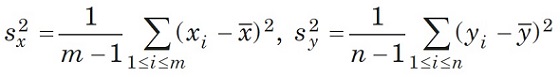
и статистику Стьюдента

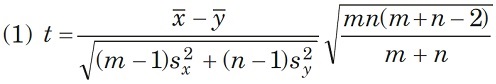
на основе которой принимают решение.

По заданному уровню значимости α и числу степеней свободы (m + n – 2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t| > t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t| < t_кр, то – принимают.

Согласно теории, должны быть выполнены два условия применимости критерия Стьюдента, основанного на использовании статистики t, заданной формулой (1): результаты наблюдений имеют нормальные распределения и дисперсии результатов наблюдений в первой и второй выборках совпадают.

Если эти условия выполнены, то статистика t при справедливости H₀ имеет распределение Стьюдента с (m + n – 2) степенями свободы. Только в этом случае описанный выше традиционный метод обоснован. Если хотя бы одно из условий не выполнено, то нет оснований считать, что статистика t имеет распределение Стьюдента.

Классические условия применимости критерия Стьюдента в подавляющем большинстве технических, экономических, медицинских и иных задач не выполнены. Тем не менее при больших и примерно равных объемах выборок его можно применять. При конечных объемах выборок традиционный метод носит неустранимо приближенный характер.

Я подсчитал очки, набранные менеджерами в двух выборках по итогам девятнадцати игровых недель, среднее х̅ , дисперсию s² и критерий Стьюдента t. Поскольку m = n, (1) можно переписать в виде:

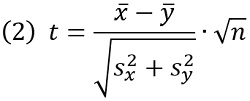
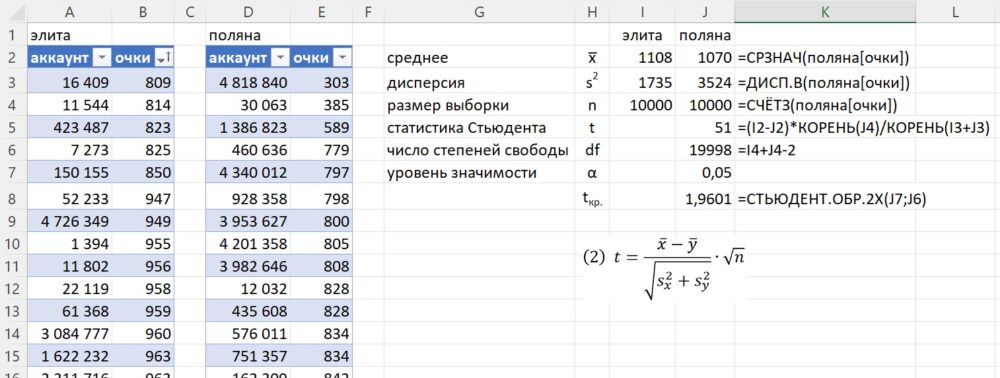
Рис. 1. Двухвыборочный критерий Стьюдента (см. также приложенный файл Excel)

Статистика Стьюдента t = 51 существенно больше t_кр=1,96. Это означает, что гипотезу однородности следует отклонить. Результаты элиты и поляны различаются.

Критерий Крамера – Уэлча равенства математических ожиданий

Вместо критерия Стьюдента для проверки H₀ целесообразно использовать критерий Крамера – Уэлча, основанный на статистике

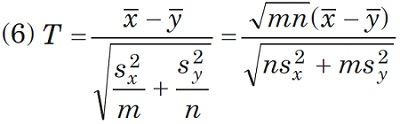
Критерий Крамера – Уэлча имеет прозрачный смысл – разность выборочных средних арифметических для двух выборок делится на естественную оценку среднего квадратического отклонения этой разности. Естественность указанной оценки состоит в том, что неизвестные статистику дисперсии заменены их выборочными оценками. Из Центральной предельной теоремы и из теорем о наследовании сходимости следует, что при росте объемов выборок распределение статистики T Крамера – Уэлча сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1: Φ(x) = N(x; 0, 1).

При m = n, как следует из формул (1) и (6), t = T. Если M(X) ≠ M(У), то при больших объемах выборок

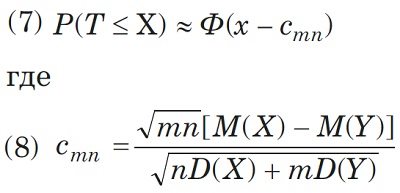
Правило принятия решения для критерия Крамера – Уэлча: если |T| ≤ Ф^-1(1 – α/2), то гипотеза однородности математических ожиданий принимается на уровне значимости α; если |T| > Ф^-1(1 – α/2), то гипотеза однородности математических ожиданий отклоняется на уровне значимости α.

Для α = 0,05 значение модуля статистики T Крамера – Уэлча надо сравнивать с граничным значением Ф^-1(1 – α/2) = 1,96.

Таким образом при анализе организационно-экономических данных более обосновано применение критерия Крамера – Уэлча, чем критерия Стьюдента. Дополнительное преимущество критерия Крамера – Уэлча по сравнению с критерием Стьюдента – не требуется равенства дисперсий D(X) = D(Y). Распределение статистики T не является распределением Стьюдента, однако и распределение статистики t, как показано выше, не является таковым в реальных ситуациях.

Поскольку размер двух выборок FPL одинаков, m = n, как было сказано выше t = T, и статистика Крамера – Уэлча ничего не добавляет к критерию Стьюдента.

Непараметрические методы проверки однородности

В большинстве задач представляет интерес не проверка равенства математических ожиданий или иных характеристик распределения, а обнаружение различия генеральных совокупностей, из которых извлечены выборки, т. е. проверка гипотезы H₀. И здесь статистики t Стьюдента и T Крамера – Уэлча не годятся. Априорное предположение о принадлежности функций распределения F(x) и G(x) к какому-либо определенному параметрическому семейству обычно нельзя достаточно надежно обосновать. Поэтому для проверки H₀ следует использовать методы, пригодные при любом виде F(x) и G(x), т. е. непараметрические методы. Непараметрический означает, что нет необходимости предполагать вид функции распределения результатов наблюдений.

Двухвыборочный критерий Вилкоксона

Этот критерий (в литературе его называют также критерием Манна – Уитни) предназначен для проверки гипотезы

где X — случайная величина, распределенная как элементы первой выборки, а Y — случайная величина, распределенная как элементы второй выборки. Альтернативой является отрицание H_0m: вероятность P(X < Y) отлична от 0,5. Это — непараметрическая гипотеза. Но из нее не следует, что функции распределения двух выборок совпадают.

Критерий Вилкоксона – один из самых известных инструментов непараметрической статистики. При альтернативной гипотезе, когда функции распределения выборок F(x) и G(x) не совпадают, распределение статистики Вилкоксона зависит от величины a = P(X < Y). Если а отличается от 1/2, то мощность критерия Вилкоксона стремится к 1 и он отличает нулевую гипотезу F ≡ G от альтернативной.

Можно переформулировать нулевую гипотезу в терминах равенства медиан двух выборок:

Тогда альтернативная двусторонняя гипотеза, просто отрицает равенство медиан

При равенстве размера двух выборок n₁ = n₂, статистика рангового критерия Вилкоксона T₁ равна сумме рангов одной из выборок (любой). Чтобы применить критерий Вилкоксона, я объединил обе выборки в одной таблице, и ранжировал аккаунты по очкам (столбцы А:С).

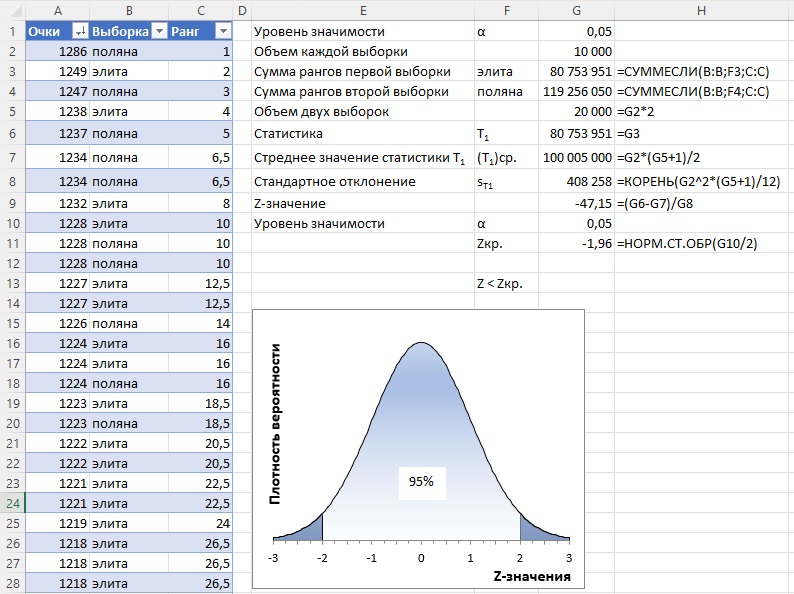
Рис. 2. Расчет критерия Вилкоксона; значения Z, попадающие в светлую область, позволяют принять нулевую гипотезу; границы равны ±1,96 Z; рассчитанное Z = -47,15 лежит далеко в области отклонения нулевой гипотезы

В качестве статистики T₁ я выбрал сумму рангов элиты (ячейка G6). Сумма n последовательных натуральных чисел по определению равна n(2n+1)/2. А выборочное среднее этой суммы задается формулой:

где n₁ – размер одной выборки, а n – размер двух выборок; n = 2∙n₁.

Выборочное стандартное отклонение:

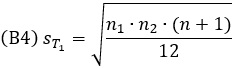
Стандартизованная Z-статистика критерия Вилкоксона для больших выборок:

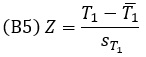
Статистика Z имеет нормальное распределение.

Статистика Z для двух выборок FPL равна минус 47,15, а Z, соответствующее уровню значимости α=0,05, минус 1,96. Z существенно меньше Zкр. Мы отклоняем нулевую гипотезу. Медиана элиты и поляны отличаются.

Состоятельные критерии проверки однородности двух независимых выборок

Это значит, что для любых отличных друг от друга функций распределения F(x) и G(x) (другими словами, при справедливости альтернативной гипотезы H₁) вероятность отклонения гипотезы H₀ должна стремиться к 1 при увеличении объемов выборок m и n. Состоятельными являются критерии Смирнова и типа омега-квадрат.

Критерий Смирнова однородности двух независимых выборок

Предполагается, что функции распределения F(x) и G(x) непрерывны. Значение эмпирической функции распределения в точке х равно доле результатов наблюдений в выборке, меньших x. Критерий Смирнова основан на использовании эмпирических функций распределения F_m(x) и G_n(x), построенных по первой и второй выборкам соответственно. Значение статистики Смирнова…

…сравнивают с соответствующим критическим значением (см., например, Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.) и по результатам сравнения принимают или отклоняют гипотезу H₀ о совпадении (однородности) функций распределения. Здесь sup – супремум – обобщение понятия максимум.

При больших объемах выборок можно воспользоваться доказанной Н. В. Смирновым в 1939 г. теоремой: в случае совпадения непрерывных функций распределения элементов двух независимых выборок

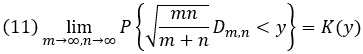
т. е. статистика

в пределе подчиняется распределению Колмогорова K(у) (подробнее см. здесь).

В нашем примере функции F(x) и G(x) являются дискретными, но шаг составляет 1/500 диапазона, так что этим ограничением можно пренебречь. Расположим аккаунты раздельно в обеих выборках по возрастанию (столбцы А:Е рис. 3).

В столбцах G:I подсчитаем количество результатов, приходящихся на очки от 800 до 1300. В столбцах K:L подсчитаем накопленные частоты, а в столбце М – абсолютное значение разности между накопленными частотами. В ячейке Р9 найдем максимум разности |F(x)–G(x)|. Критерий Смирнова рассчитаем по формуле (12) в ячейке Р10. Критическое значение статистики Колмогорова для уровня значимости α = 0,05 найдем из таблицы или в работе.

Критерий Смирнова S_C = 20,393 существенно больше статистики Колмогорова K(S) = 1,358 при α=0,05, гипотезу об однородности двух выборок можно уверенно отклонить. Результаты элиты и поляны отличаются.

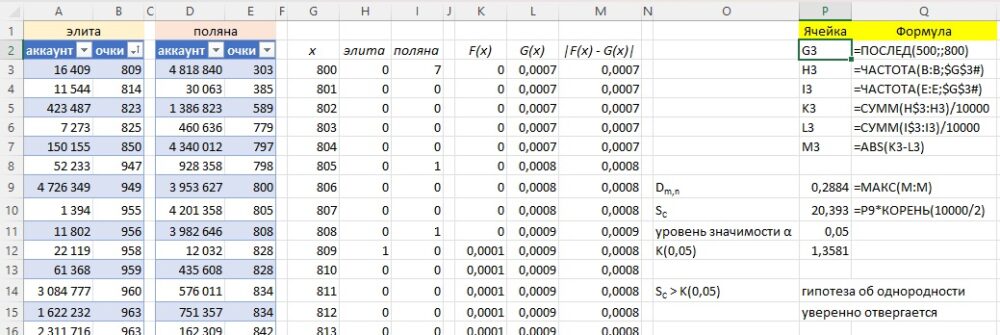
Рис. 3. Критерий Смирнова позволяет отклонить H₀

Критерий типа омега-квадрат (Лемана – Розенблатта)

Статистика критерия типа омега-квадрат для проверки однородности двух независимых выборок имеет вид:

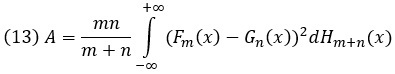
где H_m+n(x) — эмпирическая функция распределения, построенная по объединенной выборке:

Статистика A типа омега-квадрат зависит лишь от рангов элементов двух выборок в объединенной выборке. Данная статистика представляется в виде:

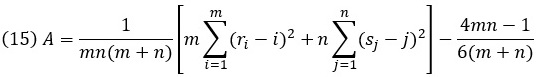
где r_i – ранг x’_i и s_j – ранг у’_j в общем вариационном ряду, построенном по объединенной выборке; здесь x’_i – элементы первой выборки x_i, переставленные в порядке возрастания.

Предел

где a₁(x) – предельная функция распределения классической статистики омега-квадрат (Крамера – Мизеса – Смирнова), используемой для проверки согласия эмпирического распределения с заданным теоретическим.

Для выборок одинакового размера n = m выражение (15) можно записать:

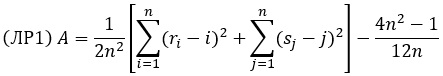
Воспользуемся объединенным рангом двух выборок. Мы сформировали его выше для расчета критерия Вилкоксона (столбцы А:С на рис. 2). Установим фильтр на столбце В – поляна. Скопируем и вставим на новом месте столбцы В и С. Пронумеруем строки – см. столбцы А:С на рис. 4. Вернемся к рис. 2, установим фильтр на столбце В – элита. Повторим копипаст. Теперь в столбцах А:С на рис. 4 у нас есть объединенный ранг двух выборок (столбец В) и раздельный ранг по каждой выборке (столбец С). Осталось реализовать вычисления по формуле (ЛР1). Получим значение статистики А омега-квадрат, равное 221,9. Критическое значение а₁ для уровня значимости α = 0,05 найдем из таблицы. А ≫ а₁, следовательно гипотезу об однородности уверенно отвергаем.

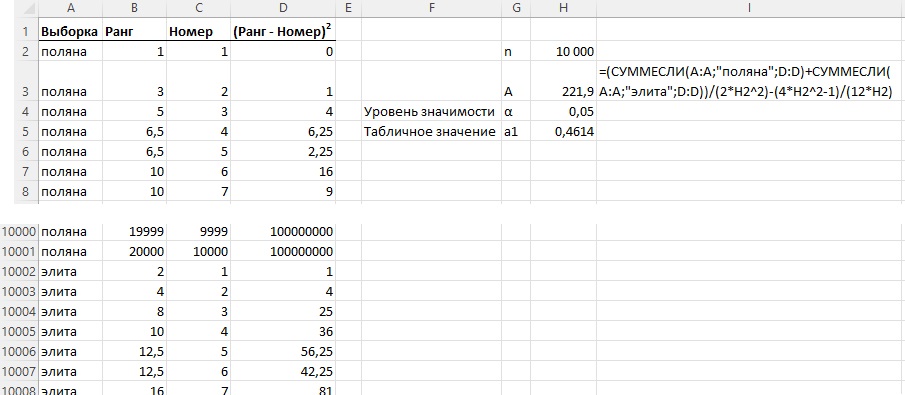
Рис. 4. Статистики омега-квадрат для двух выборок FPL

Когда какую-то мудреную статистику используешь впервые, нельзя быть уверенным, что всё сделал верно. Поэтому я решил проверить результаты. Я взял две случайные выборки по 1k из 10k аккаунтов элиты, и повторил анализ омега-квадрат.

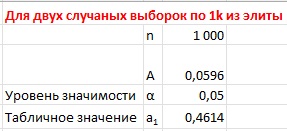
Рис. 5. Статистики омега-квадрат для двух случайных выборок из элиты

Получился ожидаемый результат: А ≪ а₁. Нет оснований отвергнуть нулевую гипотезу Н₀ об однородности выборок.

Напомню, что элита – это отобранные 10k аккаунтов ТОП рейтинга всех менеджеров FPL по итогам пяти предыдущих сезонов. Я задался вопросом: есть ли различия на уровне значимости в результатах текущего сезона между группами ТОП-1k и ТОП-2k? Среднее значение набранных очков по ТОП-1k = 1112,3, по ТОП-2k = 1109,4. Случайно ли это различие? Визуально распределения немного отличаются:

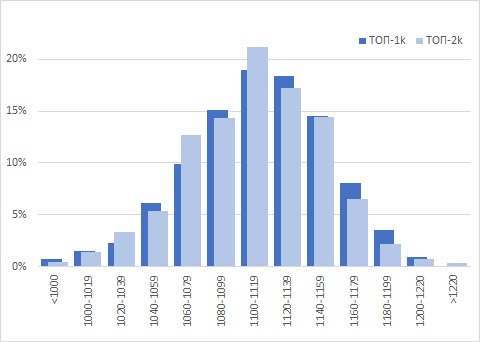
Рис. 6. Распределение текущих результатов сезона 2022/23 в группах ТОП-1k и ТОП-2k

Почти все столбцы справа от медианы более высокие у ТОП-1k. Большинство столбцов слева от медианы выше у ТОП-2k. Анализ омега-квадрат показал, что различия совсем чуть-чуть не дотянули до уровня значимости:

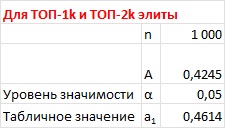
Рис. 7. Статистики омега-квадрат первой и второй подгрупп элиты

Статистика А = 0,4245 < критического а₁ = 0,4614. Выбери мы уровень значимости α = 0,1, и мы смогли бы отвергнуть Н₀. Так что ситуация зыбкая…