В книге на простых примерах рассматриваются основные понятия и теоремы теории вероятностей. В основе лежит комбинаторный подход, однако наряду с классическим определением вероятности вводится также и статистическое определение. Подробно анализируется модель случайного блуждания на прямой, описывающая физический процесс одномерного броуновского движения частиц, а также другие примеры. Обсуждаются несложные статистические задачи.
А.Н. Колмогоров, И.Г. Журбенко, А.В. Прохоров. Введение в теорию вероятностей. – М.: Издательство МЦНМО, 2015. – 168 с. (Библиотечка «Квант». Вып. 135. Приложение к журналу «Квант» №4/2015.)

Скачать краткое содержание в формате Word или pdf, примеры в формате Excel (конспект составляет около 9% от объема книги)
Купить цифровую книгу в ЛитРес
Глава 1. Комбинаторный подход к понятию вероятности
В «классическом» комбинаторном подходе вероятность какого-либо события равна отношению числа исходов, благоприятствующих этому событию, к общему числу равновозможных исходов.
Рассмотрим броуновское движение частицы по плоскости, разделенной на квадратики. Будем считать, что частица перемещается из квадратика, в котором она находится вначале, в один из четырех соседних квадратиков. Из начального положения (рис. 5а) частица может попасть в один из четырех смежных квадратиков, в каждый одним-единственным способом (рис. 5б). За два шага частица может попасть в начальное положение четырьмя способами (выходя в сторону в одном из четырех возможных направлений и возвращаясь обратно), еще в четыре квадрата частица может попасть двумя способами в каждый и в четыре квадрата – одним способом в каждый (рис. 5в). Всего частица может двигаться в течение первых двух шагов шестнадцатью различными способами. На рис. 5г указан результат аналогичного подсчета для трех шагов. Здесь число различных путей равно уже
4 + 4*9 + 8*3 = 64
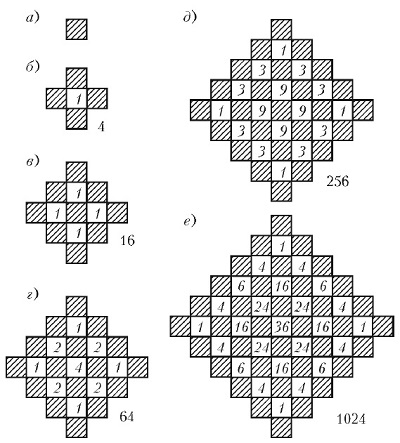
Рис. 1. Числа различных путей в блуждании по плоскости за различные промежутки времени
За t шагов частица может удалиться от начального положения не более чем на расстояние th, где h –длина стороны квадратиков. Но для этого она должна двигаться прямолинейно. При t = 5 это будет только в четырех случаях из 1024. В большинстве же случаев частица окажется в конце пути значительно ближе к своему начальному положению. Например, при t = 5 в 400 случаях (почти 40%) расстояние конечного положения от начального будет равно единице, а еще в 400 случаях это расстояние равно
![]()
Можно показать, что при любом t среднее расстояние
![]()
Здесь и далее текст, набранный с отступом – примечания Багузина. Я смоделировал броуновское движение на плоскости в Excel.
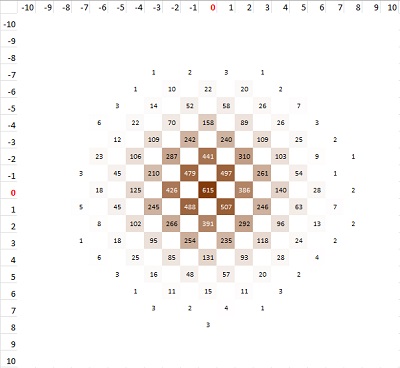
Рис. 2. Модель броуновского движения на плоскости; «частица» стартует из точки (0;0), и на каждом шаге двигается в один из четырех соседних квадратов; показана картина после 10 шагов на основе генератора случайных чисел; числа в ячейках – число испытаний, для которых «путь частицы» закончился в указанной ячейке; всего 10 000 испытаний; можно открыть приложенный Excel-файл и понажимать клавишу F9; при каждом нажатии случайные числа будут пересчитываться, что будет приводить к незначительному изменению картины
Глава 2. Вероятность и частота
Классическое определение вероятностей (комбинаторное) оправдано, когда существует возможность предсказания вероятности на основании симметрии условий, что и приводит к представлению о равновозможности. Классическое определение лишь сводит понятие вероятности к понятию равновозможности. Равновозможность представляет собой объективное свойство испытаний, определяемое условиями их проведения, но как всякое конкретное свойство, может быть установлено только с известной степенью точности. Наше представление о симметричных костях, монетах и т. п. было бы только иллюзией, если бы данные опыта не подтверждали правоту сделанных предположений.
Существует множество примеров испытаний со случайными исходами, которые могут быть повторены большое число раз в одинаковых условиях. В последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик. Назовем частотой какого-либо случайного события А в данной серии из n испытаний отношение m/n числа m тех испытаний, в которых событие А наступило, к общему их числу n. Наличие у события А вероятности, равной р, проявляется в том, что почти в каждой достаточно длинной серии испытаний частота события А приблизительно равна р.
Любая реальная монета не является идеально симметричной. И тем не менее представление об абсолютно симметричной монете очень полезно, так как во многих приложениях теории вероятностей такая модель с двумя равновозможными исходами достаточно точно описывает случайные явления, и даже точнее, чем эксперимент с подбрасыванием монеты. Статистические закономерности такого рода были впервые обнаружены на примере азартных игр. Эти наблюдения открыли путь для статистического подхода к численному определению вероятности, который особенно важен тогда, когда из теоретических соображений, подобных соображениям симметрии, значение вероятности заранее установить нельзя.
При третьем подходе к определению вероятности – аксиоматическом – вероятность задается как числовая функция Р (А) на множестве всех событий, определяемых данным экспериментом, которая удовлетворяет следующим аксиомам:
- 0 < Р (А) < 1;
- Р (А) = 1, если А достоверное событие;
- Р (А U В) = Р (А) + Р (В), где событие А U В означает осуществление или события А, или события В, причем А и В не могут произойти одновременно.
Однако ни аксиомы, ни классический и статистический подходы к определению вероятности не дают исчерпывающего определения реального содержания понятия «вероятности», а являются лишь приближениями ко все более полному его раскрытию.
Решение вопроса о практической достоверности связано с вопросом о том, какими вероятностями можно пренебрегать на практике. Этот последний вопрос решается в каждом отдельном случае по-разному и, как правило, за рамками теории вероятностей. В большинстве случаев пренебрегают уже вероятностями 0,05. Если условия практической задачи позволяют такую долю ошибок (в среднем 5 случаев на каждые 100 экспериментов), то мы считаем событие, происходящее с вероятностью 0,95, практически достоверным. В других, более деликатных, случаях принято пренебрегать лишь вероятностями 0,001, а иногда требовать и еще большего приближения вероятности отсутствия ошибки к единице. Эти рассуждения основаны на практической уверенности в том, что если вероятность события очень мала, то при однократном испытании это событие не осуществляется.
Глава 3. Основные теоремы о вероятностях
Свойства вероятности:
- Для каждого случайного события А определена его вероятность Р (А), причем 0 < Р (А) < 1.
- Для достоверного события имеет место равенство Р (Т) = 1.
- Если события А и В несовместны, то Р (А U В) = Р (А) + Р (В).
- Для противоположных событий А и А̅ имеет место равенство Р (А̅) = 1 – Р (А).
- Для невозможного события ∅ имеет место равенство Р (∅) = 0 . Для несовместных событий А и В верно Р (АВ) = 0.
- Для произвольных событий А и В Р(А U В) = Р(А) + Р(В) – Р(АВ).
Задача. Пять человек пришли в гости и оставили свои шляпы в гардеробе. Уходя, каждый из гостей взял шляпу «наудачу». Чему равна вероятность того, что каждый из гостей надел чужую шляпу?
Решение. Задача меня заинтересовала, но в книге приведен только ответ. Мы ищем вероятность получить перестановку из n элементов, чтобы никакой элемент не стоял на своём месте. Решается она формулой включений/исключений: от всех перестановок вычитаем те, где на одном месте стоит свой элемент, а остальные стоят как угодно, в том числе и на своём. Всего перестановок n! Вычитаем число перестановки, где номер гостя совпадает с номером шляпы. Таких гостей n, но готовясь к написанию рекуррентной формулы, обозначим это число через Сn1. Для каждого гостя мы допускаются любые перестановки оставшихся шляп (n – 1)! После этого имеем:
![]()
Но мы вычли лишнее – перестановки, где два элемента стоят на своих местах, значит, это количество нужно прибавить, получаем:
![]()
Продолжаем этот процесс далее, получаем итоговое количество полностью несовпадающих перестановок
![]()
Для поиска вероятности нужно разделить на количество перестановок n!
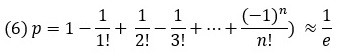
Для случая 5 шляп получаем
![]()
Элементы комбинаторики
Пример. В совокупности из М + N предметов М предметов обладают некоторым свойством А, а N предметов не обладают. Из этой совокупности предметов вынимают наудачу k предметов. Спрашивается: чему равна вероятность того, что будут извлечены m предметов со свойством А и n = k – m предметов, не обладающих этим свойством? Эта задача играет большую роль в применения демографии, статистике населения, статистическом контроле качества продукции.
Извлечь m предметов со свойством А можно СMm различными способами. Но каждый способ извлечения m предметов со свойством А может сочетаться с любым способом извлечения n предметов, не обладающих этим свойством. Следовательно, общее число благоприятствующих исходов равно СMm * СNn, а искомая вероятность равна
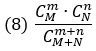
Глава 4. Последовательности испытаний Бернулли. Предельные теоремы
В самом начале формирования основных понятий теории вероятностей выяснилась фундаментальная роль одной математической модели, изученной известным швейцарским математиком Якобом Бернулли (1654–1705). Производятся последовательные испытания, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Последовательность таких независимых испытаний с двумя исходами носит название последовательности испытаний Бернулли. Вероятность ненаступления события А (наступления события А̅) в определенном испытании равна q = 1 – р. Задача найти вероятность того, что событие А наступит ровно m раз.
Вероятность того, что событие А наступит в определенных m испытаниях и не наступит в определенных n – m испытаниях, в силу теоремы умножения вероятностей для независимых событий равна pmqn–m. Но m испытаний, в которых происходит событие А, может быть выбрано из n возможных испытаний Сnm способами. Поэтому, в силу теоремы сложения вероятностей, искомая вероятность, которую мы будем обозначать символом Рn(m), равна
![]()
Эта вероятность называется биномиальной, а формул (9) – формула Бернулли. Формула Бернулли дает, в частности, вероятность того, что событие А произойдет во всех n испытаниях, и она равна
![]()
Вероятность того, что А не произойдет ни разу, равна
![]()
Исследуем теперь вероятность Рn(m) как функцию целочисленного аргумента m. Функция Рn(m) возрастает, зачем достигает максимального значения и после этого начинает убывать. Если обозначить через m* значение m, соответствующее максимальной вероятности, то будет верно неравенство
![]()
Поскольку числа np – q и np + p отличаются на 1, то либо m* равно единственному целому числу, заключенному в пределах (12), либо имеются два целых числа m*1 и m*2 такие, что
![]()
Таким образом, если величина np – q является целой, то имеются два максимальных значения вероятности Рn(nр – q) = Рn(nр + р). Если же np – q нецелое, то имеется единственное максимальное значение Рn(m) при m, равном целому числу m*, большему nр – q и меньшему nр + р.
Пример. Вероятность события А равна 3/5. Найдите наиболее вероятное число появлений события А, если число испытаний равно 19, 21.
При n = 19
![]()
Таким образом, максимальная вероятность достигается для двух значений m, равных 11 и 12. Эта вероятность равна Р19(11) = Р19(12) = 0,1797. При m = 21 максимальная вероятность достигается только для одного значения m, поскольку…
![]()
…не является целым числом. Самое вероятное значение m равно 13. Вероятность его появления равна Р21(13) = 0,1742.
Упражнение 2. В урне 9 белых и 1 красный шар. Какова вероятность того, что при 10 извлечениях (с возвращением каждого вынутого шара) будет извлечен хотя бы раз красный шар? Сколько раз нужно производить извлечение, чтобы вероятность получить хотя бы раз красный шар была не меньше 0,9?
Решение. Вероятность извлечь 10 раз подряд белый шар = (9/10)10, следовательно, вероятность, что при 10 бросках появится хотя бы один красный шар = 1 – (9/10)10 = 0,6513. Для ответа на второй вопрос запишем неравенство
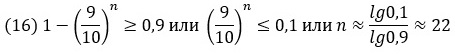
Теорема Бернулли
Мы можем теперь сформулировать и доказать одну из важнейших теорем теории вероятностей, выведенную Якобом Бернулли и опубликованную в сочинении «Искусство предположений» уже после его кончины, в 1713 году. В каждом из n независимых испытаний Бернулли с одной и той же вероятностью р может появиться некоторое событие А. Наиболее вероятное число появлений события А в n испытаниях близко к nр. Обозначим через µ число появлений события А во всех n испытаниях и рассмотрим разность µ/n – р между частотой события µ/n и его вероятностью р. Величина разности зависит от случая, поскольку р может принять любое целочисленное значение от 0 до n. Однако, чем больше n, тем реже эта разность сможет значительно отклониться от нуля. Более того, какое бы малое положительное число ε мы ни взяли, например, 0,0001 или 0,000001, при достаточно большом n разность µ/n – р по абсолютной величине окажется с большой вероятностью меньше, чем ε.
Современная формулировка закона больших чисел (теоремы Бернулли). Если вероятность наступления некоторого случайного события А в последовательности n независимых испытаний постоянна и равна р, то, каково бы ни было положительное число ε, с вероятностью, сколь угодно близкой к 1, при достаточно большом n разность µ/n – р по абсолютной величине окажется меньше, чем ε.
Упражнение 2. Велика ли вероятность того, что при 6000 бросаниях игральной кости «шестерка» выпадет не более 500 раз?
Решение. Всего возможно 66000 последовательностей выпадения кости. Один раз шестерка выпадет в…
![]()
… исходах, где первый сомножитель определяет на каком шаге выпадет шестерка, а второй число вариантов выпадения кости другими гранями. Всего же вероятность, что шестерка выпадет от 0 до 500 раз…
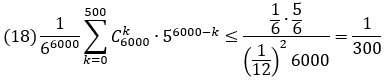
Теорема Пуассона
При n → ∞ можно вывести приближенные варианты формулы Бернулли (9). Их удобно использовать для вычисления вероятностей Рn(m) при больших значениях n. Если p(n) → 0 при n → ∞, а n∙p(n) → λ, где λ > 0, то для любого m при n → ∞
![]()
Формула (19) называется приближенной формулой Пуассона для биномиальной вероятности.
Задача о днях рождения. Найдем вероятность того, что в группе из 500 школьников ровно k родились в один определенный день, скажем, 1 июня. Можно использовать схему испытаний Бернулли с n = 500 и р = 1/365. Тогда искомая вероятность будет определяться по формуле Бернулли:
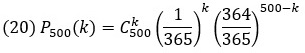
а соответствующее приближение по теореме Пуассона:
![]()
при λ = n∙p(n) = 500/365 = 1,3699.
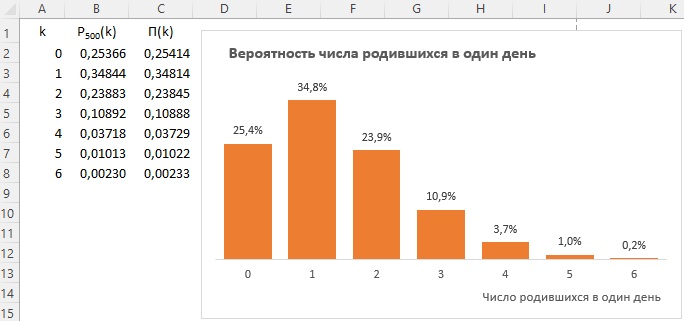
Рис. 3. Биномиальные вероятности и соответствующие приближения Пуассона в задаче о днях рождения
Упражнение 3. Книга объемом 500 страниц содержит 500 опечаток. Считая, что любая буква может быть набрана неправильно с одной и той же вероятностью, найдите вероятность того, что на заданной странице не более двух опечаток.
Решение. λ = n∙p(n) = 500/500 = 1, нас интересуют k = 0, 1 и 2. По теореме Пуассона вероятность
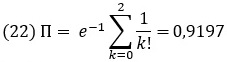
Приближенные формулы для вероятностей в случайном блуждании на прямой
Формула Бернулли (9) для р = q = ½ описывает модель случайного блуждания на прямой как вероятность сделать m шагов за первые n моментов времени. Приближенная формула для такого симметричного биномиального распределения
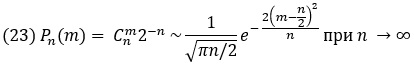
Используя (23), можно получить приближение для суммы для биномиальных вероятностей вида
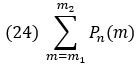
которая выражает вероятность того, что число удач в n испытаниях Бернулли находится в пределах m1 и m2. Это приближение устанавливает так называемая интегральная предельная теорема Муавра-Лапласа:
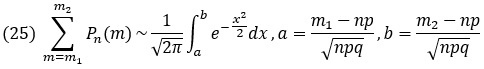
Функция
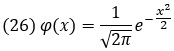
называется плотностью нормального распределения.
Глава 5. Симметричное случайное блуждание
Вернемся к случайному блужданию. Частица перемещается в дискретные моменты времени по целым точкам числовой прямой, расположенной вертикально. Будем считать, что в начальный момент времени n = 0 частица находится в начале отсчета, а в каждый следующий момент времени n = 1, 2, 3, … с равной вероятностью она совершает перемещение на единицу вверх или на единицу вниз.
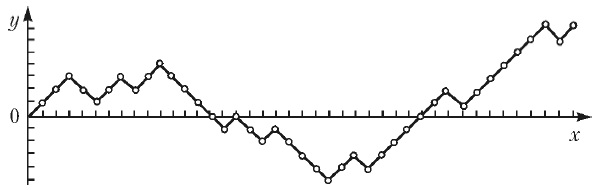
Рис. 4. Траектория движения частицы; по оси абсцисс отложено дискретное время (n шагов), по оси ординат – смещение частицы на прямой от начала координат 0
Заданные таким образом случайные блуждания демонстрируют совершенно неожиданные свойства, противоречащие, на первый взгляд, здравому смыслу.
Частица обязательно вернется в начало координат и побывает там бесконечное число раз, но (среднее) время ожидания даже первого возвращения бесконечно. С увеличением продолжительности блуждания относительное число возвращений убывает, а периоды между возвращениями возрастают по длине. Так, например, за 10 000 шагов частица побывает в нуле в среднем около 40 раз, за 1 000 000 шагов – около 400 раз, а за 100 000 000 шагов – около 4000 раз. Соответственно, среднее время между возвращениями будет меняться от 250 к 2500 и далее до 25 000.
Число возвращений растет в среднем как корень из n, а среднее время от начала блуждания до m-го возвращения в начало координат растет как m2.
Как долго частица будет в течение блуждания находиться выше или ниже оси абсцисс. Естественное, с точки зрения здравого смысла, предположение о том, что относительное время, которое частица проводит выше оси абсцисс, близко к 1/2, не подтверждается экспериментом. Оказывается, что значительную часть времени частица проводит в какой-либо одной полуплоскости. Эти парадоксальные закономерности перехода частицы с положительной стороны прямой на отрицательную и наоборот раскрываются теоремой, получившей название «закона арксинуса».
Вероятность того, что доля времени, проводимого частицей на положительной части, не превосходит α, 0 < α < 1, стремится к
![]()
Так, например, за время n = 1000 частица с вероятностью 0,1 остается на одной стороне более чем 993 момента времени и с вероятностью 0,2 – больше чем 975 моментов времени.
Глава б. Случайные величины, распределения вероятностей
Для задания случайной величины нужно знать ее значения и вероятности, с которыми эти значения принимаются. Совокупность всех различных значений, которые может принимать случайная величина, и вероятностей, с которыми она их принимает, называют распределением вероятностей случайной величины.
Полная характеристика случайной величины дается ее распределением вероятностей. Однако исключительно полезны некоторые постоянные числовые характеристики случайной величины, дающие представление о ее свойствах. Среди таких характеристик особенно большую роль играет математическое ожидание. Сумма значений случайной величины, умноженных на соответствующие вероятности, называется математическим ожиданием или средним значением случайной величины:
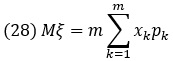
Для общего представления о распределении случайной величины важно знать не только ее математическое ожидание, но и разброс возможных ее значений относительно этого среднего значения. В теории вероятностей для измерения разброса значений случайной величины около среднего значения используют понятие дисперсии (дисперсия в переводе с латинского – «рассеяние»). Дисперсией Dξ случайной величины ξ, называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания Mξ:
![]()
Дисперсия суммы независимых случайных величин равна сумме их дисперсий.
Неравенство Чебышёва. Если случайная величина ξ имеет конечное математическое ожидание Mξ и конечную дисперсию Dξ, то при любом положительном α имеет место неравенство
![]()
Глава 7. Последовательности испытаний Бернулли: случайное блуждание и статистические выводы
Вернемся к схеме Бернулли независимых испытаний с двумя исходами. Обычно один из исходов условно называют «удачей» (событие А), а другой – «неудачей» (событие А̅). Предполагается, что в каждом испытании «удача» происходит с одной и той же вероятностью р, 0 < р < 1, а «неудача» – с вероятностью q = 1 – р. Число удач в n испытаниях Бернулли можно выразить случайной величиной Sn. Эта случайная величина имеет биномиальное распределение
![]()
Математическое ожидание – среднее число удач – равно MSn = np, а дисперсия DSn = npq.
Задача о разорении
Рассмотрим еще одну задачу, возникающую в схеме случайного блуждания. Предположим, что частица, выходящая из начала координат, блуждает на ограниченном интервале оси, а на границах этого интервала исчезает и блуждание прекращается. Какова вероятность того, что частица исчезнет в точке у = –а раньше, чем она достигнет точки у = b? Введем вероятность qn,a достижения частицей точки –a до момента времени n. Вероятности qn,a с ростом n убывают и имеют предел, который мы и называем вероятностью qa. Аналогично можно рассмотреть вероятность ра достижения частицей прямой у = b раньше, чем прямой у = –a.
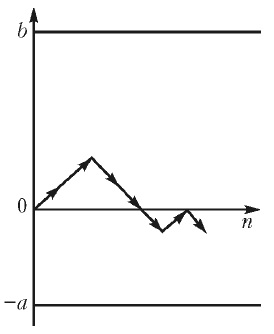
Рис. 5. Иллюстрация к задаче о разорении
Эта задача имеет широкую известность как классическая задача о разорении игрока. Традиционная постановка этой задачи такова. Представим себе, что два игрока, имея начальные капиталы а и b, играют в игру «орел и решка» или в какую-нибудь ей подобную. При этом игрок с капиталом а выигрывает в каждой партии с вероятностью р и проигрывает с вероятностью q, р + q = 1. При выигрыше он увеличивает свой капитал на 1, при проигрыше капитал его становится на 1 меньше. После некоторого числа партий может оказаться, что игрок проиграет весь свой капитал а или на руках у этого игрока будет вся сумма денег а + b. Эта ситуация и называется разорением либо первого, либо второго игрока.
Вероятность разорения игрока с капиталом а в случае одинаковых возможностей на выигрыш в каждой партии (p = q) равна
![]()
в случае неодинаковых возможностей (р ≠ q) равна
![]()
здесь λ = q/р.
В случае р = q большие шансы на разорение имеет игрок с меньшим капиталом, и его шансы на разорение тем более увеличиваются, если он менее искусен (или менее везуч) в игре. Менее тривиальны ситуацию, когда игрок, для которого результаты отдельных партий более благоприятны, играет с более богатым противником (как, например, в последней строке таблички).
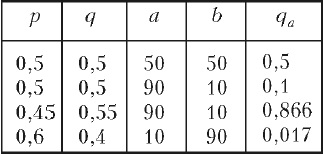
Рис. 6. Вероятность разорения в зависимости от соотношения капиталов (a и b) и шансов на успех в отдельной партии (p – вероятность успеха, q – вероятность неудачи)
Статистические выводы
Задачи, обратные задачам теории вероятностей, составляют содержание математической статистики. Типичной для математической статистики применительно к схеме Бернулли является следующая задача. Предположим, что вероятность «удачи» р заранее неизвестна и нужно определить ее по наблюдениям за исходами испытаний, которые и представляют собой статистические данные.
Пусть имеется урна с шарами двух цветов – белого и черного. Шары в урне хорошо перемешаны и доля белых шаров равна р. Предположим, что значение р неизвестно и мы должны поставить эксперимент по определению р. Будем последовательно выбирать шары из урны по одному, каждый раз возвращая шар в урну и перемешивая шары в урне перед новым извлечением. В результате получим случайную выборку некоторого фиксированного объема. При этом результаты отдельных извлечений будут взаимно независимы. При известном р и указанных условиях эксперимента вероятность получить m белых шаров в выборке объема n равна вероятности m удач (извлечение белого шара из урны – удача) в n испытаниях Бернулли с вероятностью удачи р. В рассматриваемом случае значение р неизвестно, но известно соотношение белых и черных шаров в выборке. Интуиция подсказывает, что если выборка достаточно представительна, то доля белых шаров в выборке должна быть близка к р.
Схема выбора с возвращением является частным случаем схемы Бернулли независимых испытаний. Частота «удачи» в n испытаниях есть случайная величина Sn/m со значениями m/n, где m = 0, 1, …, n.
Математическое ожидание случайной величины M(Sn/m) = р, а ее дисперсия D(Sn/m) = p(1–p)/n. Следовательно, среднее значение частоты успеха есть неизвестная вероятность успеха p, а дисперсия частоты, т. е. мера рассеяния значений частоты около p, стремится к нулю при n → ∞.
Наши выводы имеют важное, но в большей степени теоретическое значение, так как вопрос о точности оценивания неизвестной вероятности с помощью частоты решен лишь принципиально, а в каждом конкретном случае отклонения частоты от вероятности могут быть значительными. Более практичен метод оценивания неизвестной вероятности в схеме Бернулли, при котором указывается не одно, а целый интервал подходящих значений p, называемый доверительным интервалом.
Интервал с границами
![]()
называется доверительным интервалом для p с уровнем значимости α. Смысл его применения заключается в том, что, доверяясь проведенному расчету, мы утверждаем, что неизвестная вероятность p принадлежит интервалу [pнижн, pверх], а вероятность возможной ошибки, имеющей место, если этот интервал не накрывает истинное значение p, не превосходит α.