8. Статистика

Существуют две разновидности случайных переменных, [1] значения которых образуют наборы данных: категорийные и числовые (рис. 1).

Рис. 1. Разновидности данных

Категорийные случайные величины возникают в результате ответов на заданные вопросы, скажем, да или нет. Например, ответить на вопрос «Владеете ли Вы в настоящее время какими-либо акциями или облигациями?» можно лишь положительно или отрицательно. Другим примером подобных данных являются ответы на вопрос о качестве услуг, предоставляемых компанией: «Хотели бы Вы приобрести еще какие-нибудь товары в нашей компании в течение следующих 12 месяцев?». Категорийные переменные могут иметь не только два возможных значения. Например, существуют несколько вариантов ответа на вопрос: «В какой день недели вы предпочитаете обедать в ресторане?».

Подробнее »Типы данных

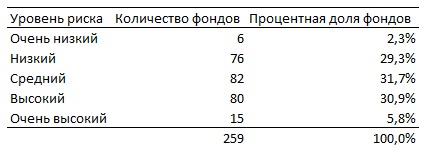
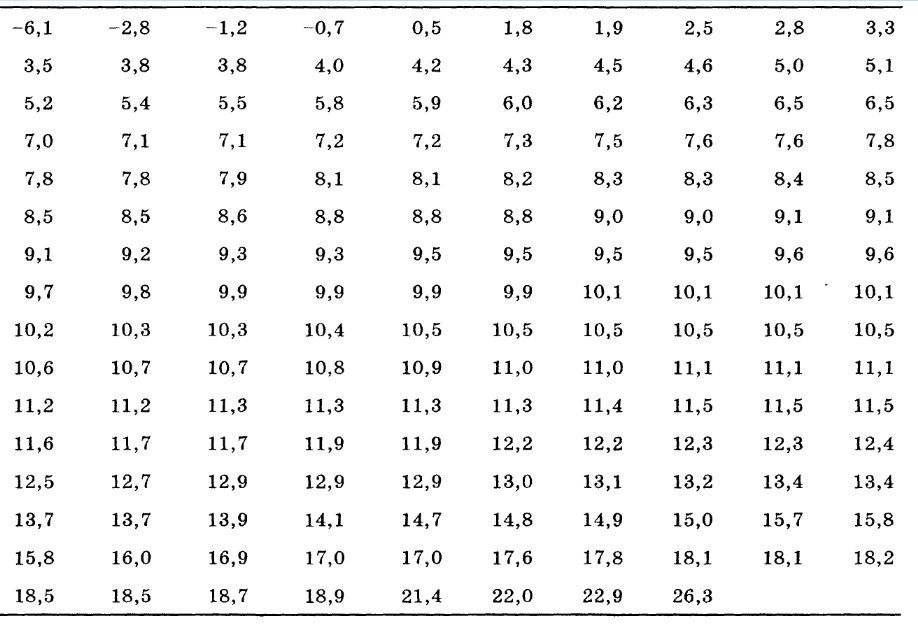
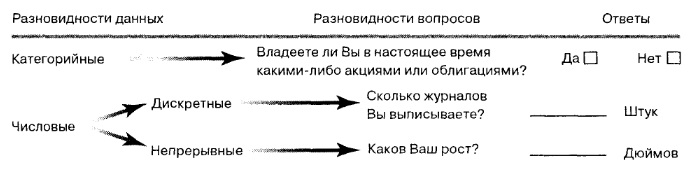
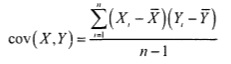Для начала несколько определений: [1] выборка — часть генеральной совокупности, извлекаемая для анализа; генеральная совокупность — множество всех рассматриваемых объектов. Вместо того, чтобы изучать всю совокупность объектов, изучают выборку, а затем результаты, полученные на выборке, распространяют на всю совокупность. Выборочные исследования занимают меньше времени, они дешевле, проще и практичнее, чем полное исследование. Например, вместо осуществления полной переписи населения, статистические процедуры выборочного исследования концентрируют внимание на сборе информации о малой репрезентативной группе, взятой из большой генеральной совокупности. Выборка, полученная в результате этих процедур, содержит информацию, которую можно использовать для оценки свойств всей генеральной совокупности.

Процедура выбора начинается с определения основы, представляющей собой полное или частичное перечисление объектов, содержащихся в генеральной совокупности. Основой могут служить источники данных, например, списки населения, каталоги или карты. Затем из основы извлекаются выборки. Если основа является неадекватной, например, вследствие того, что лица или объекты, принадлежащие генеральной совокупности, выбраны неправильно, то выборки будут неточными и тенденциозными.

Существует два вида выборок: детерминированные и вероятностные (рис. 1).

Рис. 1. Разновидности выборок

Подробнее »Методы выборки