В рамках подготовки заметки о генерировании случайных чисел в Excel обратил внимание на фундаментальный обзор Джонсона с соавторами. Первое издание книги вышло еще в 1970 г., а второе, переведенное на русский язык – в 1994. Это серьезный математический труд, но интересовавшие меня вопросы вполне доступны для понимания)) В книге подробно излагаются свойства большого числа семейств распределений. Часть I: нормальное, логнормальное, Коши, Вейбулла, χ2-, гамма-, обратное гауссовское, Парето, экспоненциальное. Часть II: логистическое, Лапласа, бета-, равномерное, экстремальных значений, F-, t-, нецентральное χ2-, нецентральное F-, нецентральное t-, распределение коэффициента корреляции, времени жизни. Издание снабжено обширной библиографией, таблицами и графиками, необходимыми для активной работы с соответствующими семействами распределений. Я представляю отдельные фрагменты, связанные с моими интересами. Дополнения Excel набраны с отступом.
Н. Л. Джонсон, С. Коц, Н. Балакришнан. Одномерные непрерывные распределения (в 2-х частях). — М.: БИНОМ. Лаборатория знаний, 2017. — 703 с. + 603 с.

Скачать заметку в формате Word или pdf, примеры в архиве (внутри 4 файла Excel)
Купить цифровую книгу в ЛитРес
ГЛАВА 12. Непрерывные распределения (общие сведения)[1]
В случае непрерывных распределений полезно нормирование, т.е. использование случайной величины
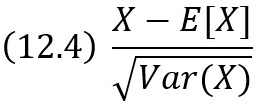
имеющей распределение с нулевым средним и единичным стандартным отклонением. В частности, форму распределения удобно описать заданием нормированных значений нескольких квантилей (т.е. значений случайной величины, в которых функция распределения принимает заданные значения). Следует различать нормированную и стандартную формы распределения. Последняя обычно удобна для получения формул, связанных с функцией плотности. Она может совпасть с нормированной формой, но это необязательно.
Кривая Лоренца
Кривая Лоренца для положительной случайной величины X является графиком отношения
![]()
в зависимости от значений FX(x). Если случайная переменная X представляет годовой доход, то величина L(p) есть доля общего дохода, полученного индивидуумами, имеющими по крайней мере 100р%-й доход. Видно, что L(p) ≤ p, L(0) = 0, L(1) = 1.
Типичная кривая Лоренца показана на рис. 12.1. Если доход всех индивидуумов равномерен, то L(p) = p. Площадь фигуры, ограниченной прямой L(p) = p и кривой Лоренца, можно рассматривать как меру неравномерности дохода или, в более общем виде, как меру изменчивости распределения случайной величины X.
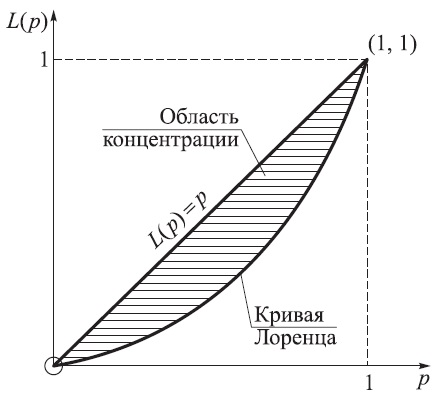
Рис. 12.1. Кривая Лоренца
Порядковые статистики
Порядковые статистики – это последовательность случайных величин, которая получается путем упорядочивания значений из выборки по их величине. Для понимания этого понятия полезно сначала вспомнить, что такое статистика и что такое выборка.
Статистика – это функция от выборки, которая используется для описания или вывода о генеральной совокупности. Примеры статистик: среднее значение, медиана, дисперсия. Выборка – набор наблюдений, полученных из генеральной совокупности.
Порядковые статистики являются функциями от выборки, которые представляют собой упорядоченные значения. Обычно они обозначаются как X1, X2, Xn, где n – размер выборки, а индекс указывает на порядковый номер в упорядоченной последовательности.
Примеры порядковых статистик:
Минимум выборки X1: Это самое маленькое значение в выборке.
Максимум выборки Xn: Это самое большое значение в выборке.
Медиана выборки X(n+1)/2: Это значение, которое делит упорядоченную выборку на две равные части.
Первый квартиль X(n+1)/4 и третий квартиль X3(n+1)/4: Это значения, которые делят упорядоченную выборку на четыре равные части.
n-ый квантиль Xp*n: Это значение, которое делит упорядоченную выборку так, что доля p наблюдений меньше этого значения.
ГЛАВА 13. Нормальное распределение
Датчики случайных чисел
В последнее время были построены многие алгоритмы, порождающие псевдо-случайные числа из нормального распределения. Конечно же для того, чтобы порождать псевдослучайные нормальные числа, можно использовать любой датчик равномерно распределенных псевдослучайных чисел в сочетании с функцией, обратной функции распределения (или ее эффективной аппроксимацией). Но были разработаны и другие, более простые, эффективные и быстрые методы; некоторые из них мы опишем здесь.
Метод Бокса–Мюллера
Исходя из двух независимых стандартных нормальных случайных величин X1 и X2 Бокс и Мюллер рассмотрели преобразование
![]()
и показали, что случайные величины Y1 и Y2 независимы и равномерно распределены в интервале (0,1). С другой стороны, если мы рассмотрим полярное преобразование
![]()
то легко проверить, что плотность совместного распределения случайных величин r и θ имеет вид:[2]
![]()
Случайные величины r и θ статистически независимы. Далее, случайные величины
![]()
независимы и равномерно распределены на (0,1). Обратив преобразование, мы получаем, что величины
![]()
представляют собой пару псевдослучайных стандартных нормальных наблюдений.
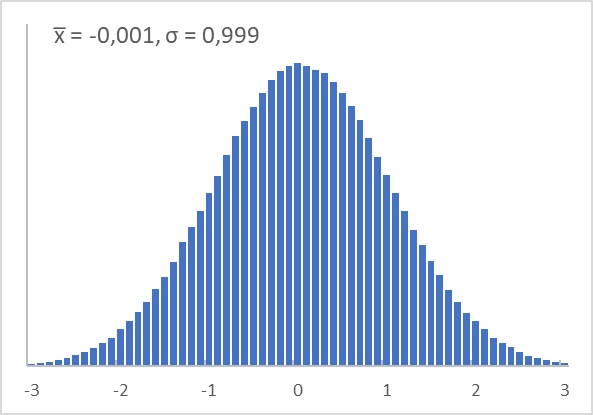
Я использовал первую формулу из (13.126) и сгенерировал 1М случайных значений. Получилось идеальное стандартное нормальное распределение (см. Excel файл 01. Метод Бокса–Мюллера):
ГЛАВА 14. Логнормальное распределение
Случайную переменную X с логнормальным распределением можно задать соотношением
![]()
где U – стандартная нормальная случайная величина, а γ, δ и θ – параметры. Из равенства (14.1) следует, что плотность распределения вероятностей случайной величины X имеет вид
![]()
Можно перейти к другим обозначениям, заменив параметры γ и δ на математическое ожидание ζ и стандартное отклонение σ случайной величины Z = ln(X – θ). Эти два набора параметров связаны соотношениями
![]()
так что равенство (14.1) можно переписать в виде
![]()
а плотность (14.2) принимает форму
![]()
В большинстве приложений «известно», что параметр θ равен нулю (так что Pr[X≤0] = 0, или X есть «положительная случайная величина»). Этот важный случай получил название двухпараметрического логнормального распределения (с параметрами γ и δ или ζ и σ). При этом формула (14.1) приобретает вид
![]()
а равенство (14.1′) выглядит так:
![]()
Для случайной величины X, подчиненной логнормальному распределению, r-й момент относительно нуля имеет вид
![]()
Математическое ожидание случайной величины X равно
![]()
а ее дисперсия составляет
![]()
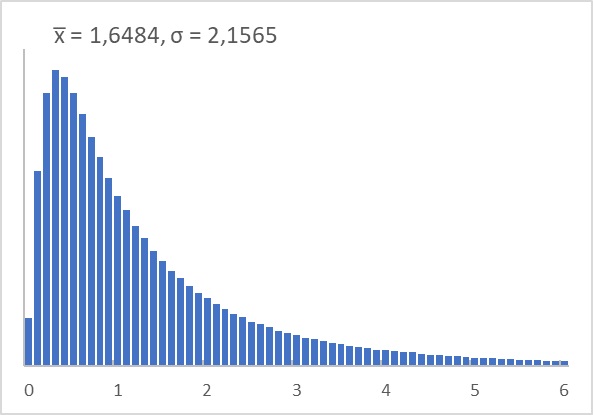
В Excel я воспользовался функцией ЛОГНОРМ.ОБР(p;μ;σ) и с помощью формулы…
=ЛОГНОРМ.ОБР(СЛМАССИВ(n;;0;1;ЛОЖЬ);μ;σ), n – число случайных значений, μ = 0 и σ = 1
…получил 1М случайных логнормальных значений. Разобрав их по карманам с шагом 0,1, получил (см. Excel файл 02. Логнормальное распределение):
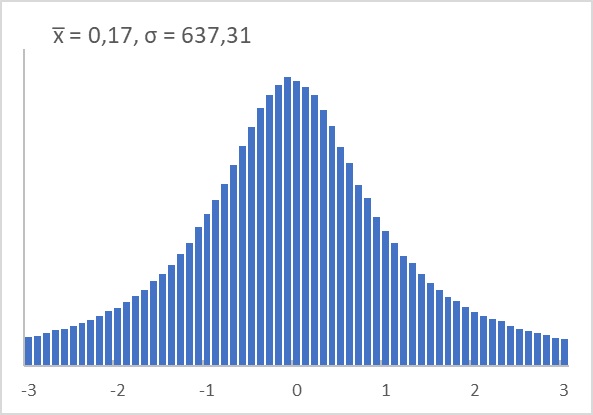
ГЛАВА 16. Распределение Коши
Удобный метод получения выборок из распределения Коши основан на обращении функции распределения F(x). Если переменная U имеет равномерное распределение в интервале (0, 1), то случайная величина tg(π(U – 1/2) подчинена стандартному распределению Коши.
В Excel я воспользовался формулой (см. Excel файл 03. Распределение Коши)
=TAN(ПИ()*(СЛМАССИВ(n;;0;1;ЛОЖЬ)-0,5)), n – число случайных значений
ГЛАВА 21. Распределение Вейбулла
Плотность распределения вейбулловской случайной переменной X:
![]()
Если положить ξ0 = 0 и α = 1, получим плотность стандартного распределения Вейбулла
![]()
и соответствующую функцию распределения
![]()
Математическое ожидание
![]()
Дисперсия
![]()
Так как функция распределения F случайной величины, подчиненной трехпараметрическому распределению Вейбулла, записывается в аналитической форме (21.4), то соответствующие псевдослучайные наблюдения легко моделировать посредством обращения этой функции распределения. А именно, положим
![]()
и, обратив это преобразование, получим
![]()
где U случайная величина равномерно распределенная в интервале (0; 1).
Другой способ моделирования наблюдения из распределения Вейбулла состоит в использовании любого эффективного датчика экспоненциально распределенных случайных чисел. В силу того что случайная величина (X – ξ0)/α имеет стандартное экспоненциальное распределение, требуемое наблюдение X из распределения Вейбулла можно получить посредством преобразования
![]()
где через Z обозначено уже смоделированное псевдослучайное наблюдение со стандартным экспоненциальным распределением.
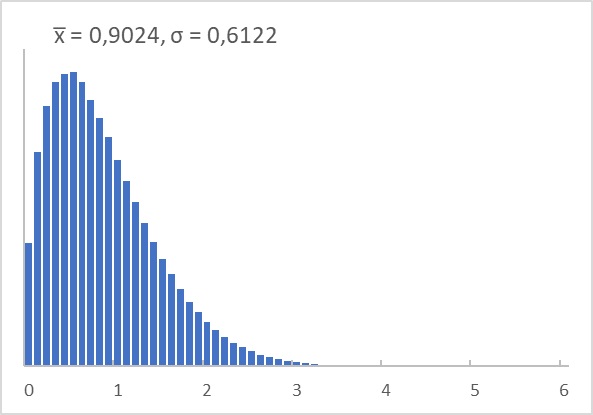
В Excel я воспользовался формулой (см. Excel файл 04. Распределение Вейбулла)
= α *-LN(1-СЛМАССИВ(n;;0;1;ЛОЖЬ))^(1/c), n – число случайных значений
[1] Главы нумеруются непрерывно. Первые 11 глав относятся к книге Одномерные дискретные распределения.
[2] В книге приведена иная формула, мне представляется, что она содержит ошибку, и я исправил.