Я подписан на рассылку издательства ДМК Пресс. Оно специализируется на литературе по программированию, но не только. Меня, в частности, интересует статистика. И книг по этой теме в издательстве немало. В недавней рассылке была анонсирована книга японских авторов Статистика в рисунках. Просматриваю оглавление и обнаруживаю раздел Форма распределения. Асимметрия и куртозис. Как же так – использовать куртозис вместо общеупотребимого русскоязычного термина эксцесс!? Гуглю, и второй ссылкой в выдаче появляется Википедия со статьей Коэффициент эксцесса. А первой – ссылка на работу Александра Цыплакова.[1] Читаю и понимаю, что не всё так однозначно))
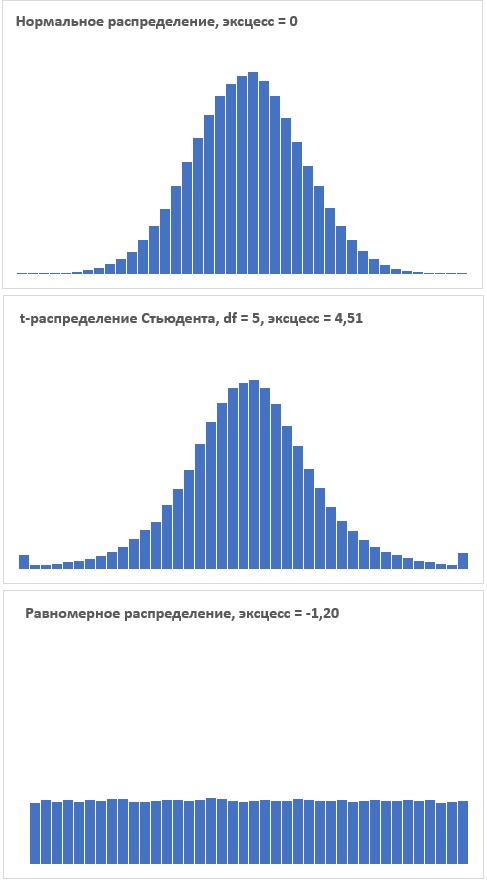
Рис. 1. Некоторые распределения и их эксцесс: а) эталонное нормальное распределение, эксцесс = 0, б) t-распределение Стьюдента, df = 5, эксцесс > 0, в) равномерное распределение, эксцесс < 0
Скачать заметку в формате Word или pdf, примеры в формате Excel
Куртозис (kurtosis) является показателем, отражающим остроту вершины и толщину хвостов одномерного распределения. Термин происходит от греческого слова κυρτός, что означает «выгнутый», «раздутый». Этот показатель строится на основе нормированного четвертого центрального момента распределения (µ4):
![]()
где µ4 = (х – х̅)4, х – случайная величина, х̅ – среднее арифметическое, σ4 – квадрат дисперсии или четвертая степень среднеквадратического отклонения. У нормального распределения k = 3, в связи с чем распространение получил модифицированный показатель:
![]()
… называемый эксцесс, excess kurtosis. Прилагательное excess в английском варианте означает «превышающий норму».
С употреблением и переводом этого слова связан ряд проблем. Во-первых, термин kurtosis может использоваться как родовое название для ряда показателей формы распределения, связанных с остротой вершины и толщиной хвостов. В частности, показатель k – 3 часто тоже называют просто kurtosis. Во-вторых, в качестве перевода термина kurtosis в русскоязычной литературе закрепилось слово эксцесс. Возможно, это связано с переводом на русский язык в 1948 г. известной книги Гаральда Крамера по статистике.[2] Крамер использовал термин excess без добавления kurtosis для показателя k – 3.
В англо-русских словарях для kurtosis предлагается перевод эксцесс. Однако ясно, что показатель k некорректно называть эксцессом, поскольку он не является излишком по отношению к 3. В связи с этим желательно переводить kurtosis на русский язык как куртозис или куртосис, a excess kurtosis как эксцесс. Слово excess в значении k – 3 в английском языке практически не употребляется, и во избежание недоразумений лучше использовать excess kurtosis.
Итак, нормальное распределение взято за эталон. Для него куртозис k = 3, а эксцесс k – 3 = 0. Распределение с положительным (избыточным) эксцессом называется островершинным. Транслитерация английского термина – leptokurtic distribution, лептокуртическое распределение – не прижилось в русском языке (Google выдал всего 134 ссылки). Лепто- означает стройный. С точки зрения формы, островершинное распределение больше чем нормальное сконцентрировано вокруг среднего значения. При этом имеет более толстые хвосты. Островершинными являются: t-распределение Стьюдента, распределение Рэлея, распределение Лапласа, экспоненциальное распределение, распределение Пуассона и логистическое распределение. Такие распределения иногда называют супергауссовыми.
Распределение с отрицательным избыточным эксцессом называется плоским или пологим (platykurtic distribution). Плати- означает широкий. С точки зрения формы плоское распределение имеет более тонкие хвосты. Плоскими являются непрерывное и дискретное равномерные распределения, а также распределение Бернулли с p = ½, для которого избыточный эксцесс равен -2.
В приложенном Excel-файле с помощью генератора случайных чисел эксцесс был рассчитан для трех распределений. Результаты представлены на рис. 1. t-распределение Стьюдента имеет очень широкие хвосты и простирается далеко за пределы, показанной на рис. 1б области по оси абсцисс. Чтобы рисунок 1б по масштабу совпадал другими рисунками, выходящие за область представления значения собраны на границах.
[1] Цыплаков, Александр (2008) «Мини-словарь англоязычных эконометрических терминов, часть 2», Квантиль, №5, стр. 41-48.
[2] Крамер, Гаральд. Математические методы статистики. М.: Мир, 1975.