Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Предыдущая глава Оглавление Следующая глава
В базах данных, первый столбец в таблице – это обычно уникальный список, называемый первичным ключом или идентификатором. Он используется, чтобы убедиться, что данные, собранные для каждого уникального элемента находятся в одном месте, и нет дублей. В Excel, однако, необработанные данные часто входит в большие наборы данных с множеством дублей. Если цель – использование формулы для подсчета уникальных элементов в списке или извлечение уникального списка, вам придется применить фантазию в работе с формулами массива, потому что в Excel нет встроенной функции, которая может выполнить эти две задачи. Эта глава посвящена формулам подсчета уникальных записей, а глава 19 – извлечению и сортировке уникальных записей.
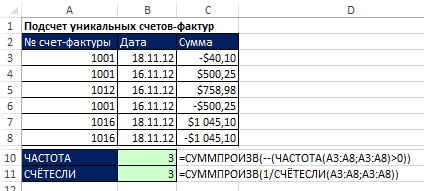
Рис. 17.1. Подсчет уникальных счетов-фактур
Скачать заметку в формате Word или pdf, примеры в формате Excel
Вот несколько типичных ситуаций, когда у вас будет много дублей, и необходимо подсчитать уникальные элементы в списке:
- Бухгалтерская таблица в разрезе артикулов, содержащая дубли в номерах счетов-фактур. Вам нужно подсчитать число уникальных счетов-фактур (любопытно, что такой вопрос был недавно задан в комментарии на сайте).
- Диаграмма Ганта или перечень проектных работ содержит дубли имен сотрудников, и вам нужно подсчитать количество сотрудников, работавших над проектом.
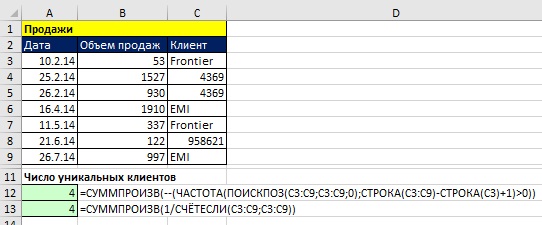
- Продажи в разрезе клиентов также содержит дубли, и вы хотите подсчитать, сколько у вас уникальных клиентов.
В главе 16 вы изучили основы использования функции ЧАСТОТА. В этой главе вы будете использовать эту функцию, как часть больших формул для подсчета уникальных вхождений в списки с дублями. Кроме того, вы увидите, как выполняет аналогичную работу функция СЧЁТЕСЛИ.
Использование формулы в одной ячейке для подсчета уникальных числовых элементов: ЧАСТОТА или СЧЁТЕСЛИ?
На рис. 17.1 показан набор данных включающий дубли счетов-фактур. Цель – подсчитать число уникальных счетов-фактур из диапазона А3:А8. Работу могут выполнить две формулы.
В ячейке В10 подсчет уникальных вхождений выполняет функция ЧАСТОТА, которая использует один и тот же диапазон для аргументов массив_данных и массив_интервалов (рис. 17.2).
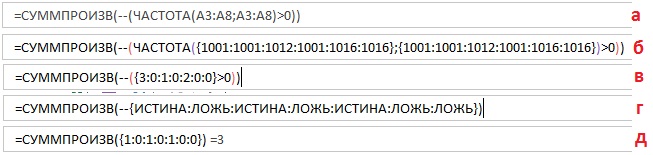
Рис. 17.2. Одинаковые диапазоны аргументов массив_данных и массив_интервалов
Подробнее о работе формулы =СУММПРОИЗВ(-(ЧАСТОТА(A3:A8;A3:A8)>0))
(Чтобы наблюдать работу формулы шаг за шагом, пройдите по меню ФОРМУЛЫ –> Вычислить формулу).
(б) Массив_данных и массив_интервалов возвращают один и тот же массив значений из диапазона А3:А8.
(в) Поскольку массив_интервалов состоит только из чисел, первое появление значения массива интервалов (например, 1001) вернет число вхождений в него из массива данных (три раза). Второе и третье появление массива интервалов (1001) вернет нули.
(д) Двойное отрицание превращает логические значения в числовые.
(е) Функция СУММПРОИЗВ позволяет избежать ввода формулы с помощью Ctrl+Shift+Enter.
Теперь давайте взглянем на формулу СЧЁТЕСЛИ (рис. 17.3). И здесь области аргументов диапазон и критерий одинаковые.
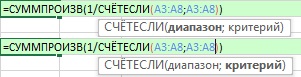
Рис. 17.3. Одинаковые диапазоны аргументов диапазон и критерий функции СЧЁТЕСЛИ
Подробнее о работе формулы =СУММПРОИЗВ(1/СЧЁТЕСЛИ(A3:A8;A3:A8))
(а) Поскольку аргумент критерий функции СЧЁТЕСЛИ ожидает одно значение, а вместо этого вы даете ему несколько значений, функция СЧЕТЕСЛИ возвращает массив.
(б) Вы даете аргументу критерий шесть значений, и поэтому СЧЁТЕСЛИ дает шесть ответов. Поскольку вы ввели одинаковые ссылки в оба аргумента, функция СЧЁТЕСЛИ подсчитывает для каждого элемента аргумента критерий количество вхождений из аргумента диапазон. В том числе, и для дублирующих критериев. Это отличается от работы функции ЧАСТОТА, которая игнорировала дубли. Напоминаю, что несколько значений в аргументе диапазон, не превращает СЧЁТЕСЛИ в функцию массива (такая ситуация для этой функции является стандартной). А вот несколько значений в аргументе критерий делает из СЧЁТЕСЛИ функцию массива.
(в) Функция СЧЁТЕСЛИ возвращает массив количеств вхождения. Например, поскольку счет-фактура №1001 находится в ячейках A3, А4, и А6, результирующий массив содержит значение 3 в этих трех относительных позициях. Операция «1/массив» превращает этот бессмысленно большой подсчет в то, что нужно: 1/3+1/3+1/3 = 1, т.е. «правильное» уникальное число для №1001.
(г) Функция СУММПРОИЗВ возвращает сумму произведений двух массивов: единицы деленной на СЧЁТЕСЛИ.
5000 строк формула с функцией ЧАСТОТА справляется за 0,03 с, а с функцией СЧЁТЕСЛИ – за 1,8 с. В 60 раз медленнее!
Использование формулы в одной ячейке для подсчета уникальных текстовых или смешанных элементов: ЧАСТОТА или СЧЁТЕСЛИ?
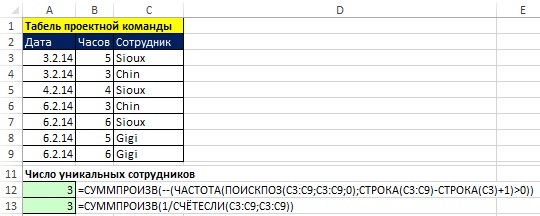
На рис. 17.5 табель содержит повторяющиеся имена сотрудников. Цель – подсчитать количество уникальных имен в диапазон С3:С9. Как и выше задача решена с помощью функций ЧАСТОТА и СЧЁТЕСЛИ. Обратите внимание:
- Формула с функцией СЧЁТЕСЛИ такая же, как и выше для числовых данных (см. рис. 17.3).
- Формула с функцией СЧЁТЕСЛИ намного проще в написании, чем формула с ЧАСТОТА.
- Если бы в столбце Сотрудники были также числовые данные, формулы не изменились бы (рис. 17.6).
Рис. 17.5. Формулы для подсчета уникальных текстовых элементов данных. Столбец Сотрудники содержит текстовые данные
Рис. 17.6. Формулы для подсчета уникальных смешанных элементов данных
Несмотря на то, что формула с функцией ЧАСТОТА длиннее, чем с функцией СЧЁТЕСЛИ, первая формула работает гораздо быстрее.
Подробнее о том, как работает формула
=СУММПРОИЗВ(--(ЧАСТОТА(ПОИСКПОЗ(C3:C9;C3:C9;0);СТРОКА(C3:C9)-СТРОКА(C3)+1)>0))
ПОИСКПОЗ находит относительный номер позиции в массиве, соответствующий первому вхождению каждого элемента (третий аргумент – тип_сопоставления = 0 – определяет точный поиск).
Для нашего набора данных {"Frontier":4369:4369:"EMI":"Frontier":958621:"EMI"}, ПОИСКПОЗ вернет {1:2:2:4:1:6:4}. Обратите внимание, что в возвращаемом массиве значений позиций есть дубли, а уникальных значений – четыре: 1, 2, 4, 6. Вы используете массив {1:2:2:4:1:6:4} в качестве аргумента массив_данных функции ЧАСТОТА.
Фрагмент формулы СТРОКА(C3:C9)-СТРОКА(C3)+1 возвращает массив {1;2;3;4;5;6;7}, который помещен в аргументе массив_интервалов функции ЧАСТОТА.

ЧАСТОТА({1:2:2:4:1:6:4};{1:2:3:4:5:6:7}) возвращает массив {2:2:0:2:0:1:0:0}.
Обратите внимание, что аргумент массив_данных функции ЧАСТОТА содержит две единицы. Именно поэтому первый элемент в результирующем массиве 2. Два – это число единиц.
Массив {2:2:0:2:0:1:0:0} дает вам трафарет: «числа больше нуля указывают на первое вхождение элемента». Единица впервые появляется в первой позиции, двойка – во второй, тройка – отсутствует, четверка – в четвертой, пятерка – отсутствует, шестерка – в шестой, семерка и более чем семерка – отсутствуют.
Сравнение массива {2:2:0:2:0:1:0:0} с нулем позволяет вернуть массив истинных и лживых значений: {ИСТИНА:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ЛОЖЬ}, а двойное отрицание превращает логические значения в численные: {1:1:0:1:0:1:0:0}.
Поскольку функция СУММПРОИЗВ содержит только один массив, ей нечего умножать, и она просто суммирует единицы, возвращая значение 4. Для этого подошла бы и функция СУММ:
{=СУММ(--(ЧАСТОТА(ПОИСКПОЗ(C3:C9;C3:C9;0);СТРОКА(C3:C9)-СТРОКА(C3)+1)>0))}
Но последняя требует ввода с помощью Ctrl+Shift+Enter, чего при случае всегда удобно избегать.
Что делать, если в диапазоне есть пустые ячейки?
Этот пример аналогичен предыдущему, но в ячейке С8 пусто. Предыдущие формулы (см. рис. 17.6) возвращают ошибки, так что нужно исключить из подсчетов пустые ячейки (рис. 17.8).
Рис. 17.8. Формулы подсчета уникальных элементов при наличии пустых ячеек в диапазоне. Эти формулы будут работать, если в ячейке нулевая текстовая строка =»».
Пройдите по меню ФОРМУЛЫ –> Вычислить формулу, и проследите, как работают фрашменты этих двух формул.
Использование формулы в одной ячейке для подсчета уникальных элементов с более, чем одним условием
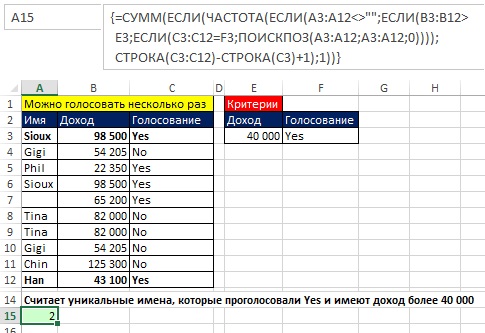
Если вам нужно выбрать не все уникальные имена, а наложить на выбор некоторые условия, формула усложняется. На рис. 17.9 каждый мог проголосовать несколько раз. Цель – подсчет уникальных имен избирателей (пропуская пустые ячейки), доход которых превышает 40 000, проголосовавших «за».
Рис. 17.9. Подсчет уникальных голосов «за», основанный на двух условиях; формула в ячейке А15 отображена в строке формул
Как использовать подстановочные знаки
Вот что сказано в справке Microsoft по функции СЧЁТЕСЛИ в разделе «Использование подстановочных знаков». В критерии можно использовать подстановочные знаки: вопросительный знак (?) и звездочку (*). Вопросительный знак соответствует одному любому символу, а звездочка — любой последовательности знаков. Если требуется найти непосредственно вопросительный знак (или звездочку), необходимо поставить перед ним знак тильды (~). На рис. 17.12 показано, как это работает.
Рис. 17.12. Использование «~» позволяет формуле «увидеть» * как симаол, а не подстановочный знак
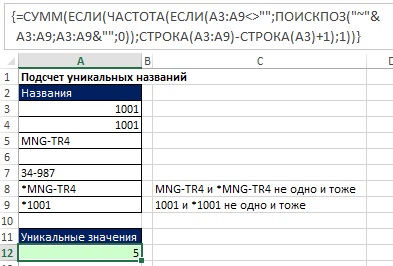
На рис. 17.13 показано, как можно создать формулу подсчета уникальных значений, которая воспринимает «*», как символ, а не подстановочный знак.
Рис. 17.13. Формула подсчета уникальных значений, распознающая *, как знак; формула в ячейке А12 отражена в строке формул
Примечание: Если вы попытаетесь создать формулу типа =СУММПРОИЗВ(--(A3:A9<>"")/СЧЁТЕСЛИ("~"&A3:A9;A3:A9&"")), вы потерпите неудачу, так как аргумент диапазон функции СЧЁТЕСЛИ не поддерживает операторы массива.
Рис. 17.14. Сравнение методов подсчета уникальных значений
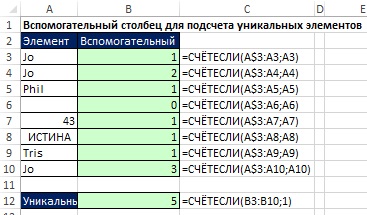
Использование вспомогательного столбца для подсчета уникальных элементов
Сначала во вспомогательном столбце определяется число соответствий значений из всё расширяющегося диапазона критерию. Далее в ячейке А12 просто подсчитывается число единиц во вспомогательном столбце (первое вхождение – уникальное). Это решение легко создать, оно игнорирует пустые ячейки, и работает с различными типами данных. Однако, для больших наборов данных, расчеты занимают много времени, поскольку расширенный диапазон означает наличие большого числа ссылок. Так же не всегда можно создать вспомогательный столбец.
Рис. 17.15. Использование вспомогательного столбца
На рис. 17.16 показан пример подсчет уникальных записей в наборе данных, когда есть несколько дублей.
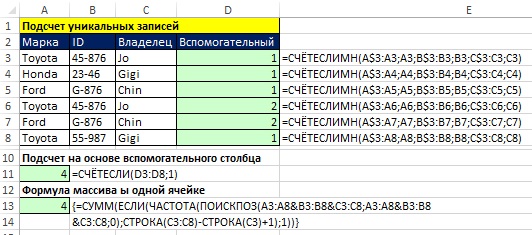
Рис. 17.16. Вспомогательный столбец для подсчета уникальных записей в наборе данных








Добрый день, столкнулся с такой особенность функции ЧАСТОТА, кстати, у вас она [особенность] в статье встречается тоже.
Формула применяется на диапазон размерностью [7:1] (7 строк, 1 столбец), а на выходе у нее 8! значений, которые отрабатывают условие > 0. Так-то в рамках этой функции 8-й элемент всегда = 0, ошибки нет, кол-во уникальных значений посчитает корректно.
Однако, из-за этой «особенности» становится невозможным ее применение с функциями внутри СУММПРОИЗВ, когда предварительно диапазон проверяется на одно, два, три условия, а затем среди отфильтрованного диапазона считается еще кол-во уникальных значений через ЧАСТОТУ, у которой кол-во элементов всегда больше диапазона на +1. Результатом работы такой функции всегда будет #Н/Д.
Может кто-нибудь объяснить логику, почему результат работы функции ЧАСТОТА всегда имеет +1 элемент от заданного диапазона?
>Может кто-нибудь объяснить логику, почему результат работы функции ЧАСТОТА всегда имеет +1 элемент от заданного диапазона?
Посмотрите Глава 16. Функция массива ЧАСТОТА. В начале заметки описано, почему это так.