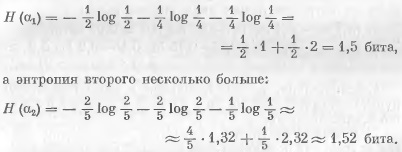Информация не являлась научным понятием, пока ее не научились измерять. Единица информации – бит – это количество информации, содержащееся в вопросе, на который равновероятны два ответа: да и нет. Извлекая информацию, мы уменьшаем энтропию – меру неопределенности системы. Некоторые следствия теории информации не тривиальны, и могут быть полезны менеджерам. Например, если на вопрос существует только два ответа, то максимальная информация может быть получена, если вероятность ответов одинакова. Если у системы много состояний, то существенный вклад в энтропию системы дают только состояния, вероятность реализации которых наибольшая. Книга Вероятность и информация – относительно доступное введением в теорию информации (область математики). Для чтения книги достаточно математической подготовки в объеме школьного курса.
Исаак Яглом, Акива Яглом. Вероятность и информация. М.: Наука, 1973. – 512 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon
Глава I. Вероятность
§ 1. Определение вероятности. Случайные события и случайные величины
Рассмотрим какое-либо событие, определяемое результатами опыта. Если это событие осуществляется при m из n возможных равновероятных исходов опыта и не осуществляется при остальных n – m исходах, то вероятность его принимается равной m/n. Другими словами, вероятность некоторого события равна отношению числа равновероятных исходов, благоприятных для данного события, к общему числу равновероятных исходов.
§ 2. Свойства вероятности. Сложение и умножение событий. Несовместимые и независимые события
Если события А и В несовместимы, т.е. сразу оба они не могут иметь места, то
р(А+В) = р(А) + р(В)
Если события А и В совместимы, т.е. могут реализоваться одновременно
р(А+В) = р(А) + р(В) – р(АВ),
где р(АВ) – вероятность одновременного наступления событий А и В.
Если события А и В независимы, то
Р(АВ) = р(А)∙р(В)
Среднее значение суммы двух случайных величин равно сумме их средних значений:
ср. зн. (α + β) = ср. зн. α + ср. зн. β
Для независимых случайных величин среднее значение их произведения равно произведению средних значений этих величин:
ср. зн. (α∙β) = (ср. зн. α) ∙ (ср. зн. β)
§ 3. Условные вероятности
Вероятность, которую имеет событие В том случае, когда известно, что событие А имело место, мы будем называть условной вероятностью события В при условии А и обозначать через рА(В).
Условная вероятность рА(В) какого-либо события В при определенном условии А может быть и меньше и больше безусловной вероятности р(В) этого события (т.е. вероятности, которую имеет В, если про результат опыта, с которым связано А, ничего неизвестно).
Если события А и В независимы, то, очевидно, рА(В) = р(В). Последнее условие даже можно считать точным математическим определением понятия независимости событий, позволяющим для любой пары событий А и В проверить, являются ли они независимыми или нет.
Для зависимых событий А и В:
(1) р(АВ) = р(А)∙рА(В)
Это и есть общее правило для определения вероятности произведения АВ двух событий; его также часто называют правилом умножения вероятностей (то правило, которое мы называли правилом умножения в § 2, является его частным случаем).
Из формулы (1) следует, что
р(А)∙рА(В) = р(В)∙рВ(А)
ибо события АВ и ВА, разумеется, не отличаются). Отсюда вытекает
р(В) = р(А)∙рА(В) + р(А̅)∙рА̅(В)
Если какой-либо опыт α может иметь k (и только k) попарно несовместимых исходов A1, А2, …, Аk, то любое событие В можно представить в виде суммы событий A1B + А2В + … + АkВ и
Эта формула называется формулой полной вероятности.
§ 4. Дисперсия случайной величины. Неравенство Чебышева и закон больших чисел
Принято характеризовать разброс случайной величины средним значением квадрата ее отклонения от своего среднего значения а. Полученное таким образом число называется дисперсией случайной величины α:
дисп. α = ср. зн. (α – а)2
Если, например, случайная величина а измеряется в км, то и ее среднее значение имеет размерность км, а дисперсия — размерность км2. Поэтому наряду с дисперсией часто рассматривают число, равное корню квадратному из дисперсии случайной величины. Это число называется средним квадратичным уклонением случайной величины. Оно измеряется в тех же единицах, что и сама случайная величина а, и также служит мерой «разброса» ее значений.
Можно показать, что
дисп. α = ср. зн. (α2) – (ср. зн. α)2
Дисперсия суммы двух независимых случайных величин всегда равна сумме их дисперсий.
Если α — число осуществлений некоторого события А в последовательности n взаимно независимых испытаний, причем вероятность осуществления А при каждом испытании равна р, то
ср. зн. α = nр
дисп. α = nр (1 – р)
Отсюда вытекает одно весьма полезное следствие. Дисперсия среднего арифметического в n раз меньше дисперсии каждой из рассматриваемых случайных величин. Это вплотную подводит нас к одному замечательному неравенству. Если α – случайная величина со средним значением а и дисперсией d, то всегда
Здесь ε – произвольное положительное число; запись же P(|α –a| > ε) означает вероятность того, что значение случайной величины α отклонится от среднего значения а той же величины больше чем на ε. Неравенство (4) называется неравенством Чебышева; оно показывает, что чем меньше дисперсия d случайной величины α, тем меньше вероятность значительного отклонения α от числа а = ср. зн. α.
Если α — число осуществлений при n независимых испытаниях некоторого события А, вероятность осуществления которого при одном, испытании равна р, то при любом ε > 0
При любом положительном ε мы можем найти столь большое N, что неравенство n > N «практически гарантирует» то, что отклонение частоты α/n от вероятности р будет меньше ε. Это заключение носит название закона больших чисел.
Глава II. Энтропия и информация
§ 1. Энтропия как мера степени неопределенности
Главным свойством случайных событий является отсутствие полной уверенности в их наступлении, создающее известную неопределенность при выполнении связанных с этими событиями опытов. Для практики важно уметь численно оценивать степень неопределенности самых разнообразных опытов, чтобы иметь возможность сравнить их с этой стороны. За единицу измерения степени неопределенности принимается неопределенность, содержащаяся в опыте, имеющем два равновероятных исхода (например, в опыте, состоящем в подбрасывании монеты и выяснении того, какая сторона ее оказалась сверху, или в выяснении ответа «да» или «нет» на вопрос, по поводу которого мы с равными основаниями можем ожидать, что ответ будет утвердительным или отрицательным). Такая единица измерения неопределенности битом (в немецкой литературе используется также выразительное ее название «Ja-Nein Einheit («да-нет единица»).
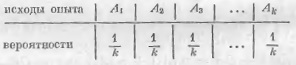
В самом общем случае, для опыта α с таблицей вероятностей
мера неопределенности равна
– р (A1) ∙ log р (A1) – р (A2) ∙ log р (A2) – … – р (Ak) ∙ log р (Ak)
Это последнее число мы, руководствуясь некоторыми глубокими физическими аналогиями, несущественными, впрочем, для всего дальнейшего, будем называть энтропией опыта α и обозначать через Н(α).
Так как –р∙log р равно нулю лишь при р = 0 или р = 1, то ясно, что энтропия Н(α) опыта α равна нулю лишь в том случае, когда одна из вероятностей р(А1), р(А2), …, р(Аk) равна единице, а все остальные равны нулю. Это обстоятельство хорошо согласуется со смыслом величины Н(α) как меры степени неопределенности: действительно, только в этом случае опыт вообще не содержит никакой неопределенности.
Далее, естественно считать, что среди всех опытов, имеющих k исходов, наиболее неопределенным является опыт с таблицей вероятностей:
В этом случае предсказать исход опыта труднее всего. Этому отвечает то обстоятельство, что такой опыт имеет наибольшую энтропию. Для k = 2 функция
H(p) = –p∙log р – (1 – p)∙log (1 – р),
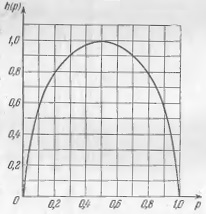
определяющая энтропию опыта с двумя исходами (вероятности которых равны р и 1 – р), принимает наибольшее значение (равное log2 = 1) при р = ½. На рис. 1 изображен график этой функции, показывающий, как меняется энтропия h(р) при изменении р от 0 до 1.
Рис. 1. Зависимость энтропии h(р) от вероятности р для k = 2
Задача 1. Имеются две урны, содержащие по 20 шаров — 10 белых, 5 черных и 5 красных в первой и 8 белых, 8 черных и 4 красных во второй. Из каждой урны вытаскивают по одному шару. Исход какого из этих двух опытов следует считать более неопределенным?
Таблицы вероятностей для соответствующих опытов (обозначим их через α1 и α2) имеют вид: опыт α1 (извлечение шара из 1-й урны):
опыт α2 (извлечение шара из 2-й урны):
Энтропия первого опыта равна
Поэтому, если оценивать степень неопределенности исхода опыта его энтропией, то надо считать, что исход второго опыта является более неопределенным, чем исход первого.
Исторически первые шаги к введению понятия энтропии были сделаны еще в 1928 г. американским инженером-связистом Хартли, предложившим характеризовать степень неопределенности опыта с k различными исходами числом log k. К сожалению, предложенная им мера степени неопределенности, полностью игнорирует различие между характером имеющихся исходов (почти невероятному исходу здесь придается такое же значение, как и исходу весьма правдоподобному).
Ошибочность точки зрения Хартли была показана Клодом Шенноном, предложившим принять в качестве меры неопределенности опыта α с возможными исходами А1, А2, …, Ak величину
Н(α) = – р (A1) ∙ log р (A1) – р (A2) ∙ log р (A2) – … – р (Ak) ∙ log р (Ak)
где р (A1), р (A2), …, р (Ak) – вероятности отдельных исходов; он же предложил называть эту величину энтропией.
Следует, однако, иметь в виду, что мера Шеннона не может претендовать на полный учет всех факторов, определяющих «неопределенность опыта» в любом смысле, какой может встретиться в жизни. Так, например, мера Н(α) зависит лишь от вероятностей р (A1), р (A2), …, р (Ak) различных исходов опыта, но вовсе не зависит от того, каковы сами эти исходы — являются ли они в некотором смысле «близкими» один к другому или очень «далекими».
Особенность энтропии Н(α) объясняется тем, что понятие энтропии первоначально было введено специально для решения некоторых вопросов теории передачи сообщений по линиям связи. При этом, конкретное содержание самого сообщения совершенно несущественно, и проявляется в независимости энтропии Н(α) от значений A1, A2, …, Ak самих исходов опыта.
§ 2. Энтропия сложных событий. Условная энтропия
Пусть α и β — два независимых опыта с таблицами вероятностей: опыт α
Тогда
Н(αβ) = Н(α) + Н(β)
(правило сложения энтропий), которое хорошо согласуется со смыслом энтропии как меры степени неопределенности.
Предположим теперь, что опыты α и β не независимы (например, что α и β — последовательные извлечения двух шаров из одной урны). Тогда:
Н(αβ) = Н(α) + Нα(β)
где Нα(β) – среднее значение случайной величины, принимающей с вероятностями р (A1), р (A2), …, р (Ak) значения НA1(β), НA2(β), …, НAk(β), т. е. значения, равные условной энтропии опыта β при условии, что опыт α имеет исходы A1, A2, …, Ak. Средняя условная энтропия Нα(β), вычисление которой не предполагает известным исход α, глубоко отражает взаимную зависимость опытов α и β.
Условная энтропия Нα(β) заключается между нулем и энтропией Н(β) опыта β (безусловной):
0 ≤ Нα(β) ≤ Н(β)
Таким образом, случаи, когда исход опыта β полностью определяется исходом α и когда опыты α и β независимы, являются в определенном смысле крайними.
§ 3. Понятие об информации
Равенство Н(β) нулю означает, что исход опыта β заранее известен; большее или меньшее значение числа Н(β) отвечает большей или меньшей проблематичности результата опыта. Какое-либо измерение или наблюдение α, предшествующее опыту β, может ограничить количество возможных исходов опыта β и тем самым уменьшить степень его неопределенности. Тот факт, что осуществление α уменьшает степень неопределенности β, находит свое отражение в том, что условная энтропия Нα(β) опыта β при условии выполнения α оказывается меньше первоначальной энтропии Н(β) того же опыта. Таким образом, разность
I (α, β) = Н (β) – Нα (β)
указывает, насколько осуществление опыта α уменьшает неопределенность β, т.е. как много нового узнаем мы об исходе опыта β, произведя измерение (наблюдение) α; эту разность называют количеством информации относительно опыта β, содержащимся в опыте α. Таким образом, мы получаем возможность численного измерения информации.
Информация относительно β, содержащаяся в опыте α, по определению представляет собой среднее значение случайной величины Н (β) – НAi (β), связанной с отдельными исходами Аi опыта α; поэтому ее можно было бы назвать также «средней информацией относительно β, содержащейся в α». При этом рекомендуется начинать с того опыта α0, который содержит наибольшую информацию относительно β, ибо при ином опыте α мы вероятно, добьемся менее значительного уменьшения степени неопределенности β – энтропии H(β). Случайный характер исходов опыта β не позволяет заранее указать кратчайший путь к выяснению результата этого опыта: самое большее, на что мы можем рассчитывать – это указать путь, который вероятнее всего окажется кратчайшим; именно эту возможность и предоставляет теория информации (я решил эту задачу для игры Быки и коровы. – Прим. Багузина).
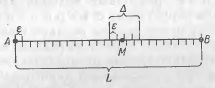
Задача 1. Пусть опыт Р состоит е определении положения некоторой точки М, относительно которой заранее известно только, что она расположена на отрезке АВ длины L (рис. 2), а опыт α — в измерении длины отрезка AM с помощью некоторого измерительного прибора, дающего нам значение длины с точностью до определенной «ошибки измерения» Δ (например, с помощью линейки, на которой нанесена шкала с делениями длины Δ). Чему равна информация I(α, β), содержащаяся в результате измерения, относительно истинного положения точки M?
Рис. 2. Измерение с точностью Δ
Разобьем весь отрезок АВ на маленькие отрезки длины ε, выбранной так, чтобы и на всем отрезке АВ и на отрезке длины Δ уложилось целое число таких малых отрезков (т.е. чтобы отношения L/ε и Δ/ε оба выражались целыми числами). Поставим задачу об определении положения точки М с точностью до величины ε. Так как заранее нам было известно только, что точка М располагается где-то на отрезке АВ, то мы можем считать, что опыт β, состоящий в определении ее положения с точностью до ε, имеет L/ε равновероятных исходов, так что его энтропия равна Н (βε) = log (L/ε).
После того как мы произвели опыт α, т.е. измерили длину AM с помощью нашего измерительного прибора, мы выяснили, что на самом деле точка М помещается внутри меньшего интервала длины Δ (определяющего точность измерения); поэтому при известном исходе α опыт βε будет иметь уже всего Δ/ε равновероятных исходов, так что Нα (βε) = log (Δ/ε). Следовательно,
Приравняв энтропию Н(α) средней информации, содержащейся в исходе опыта α, мы можем, в частности, предположить, что передача сообщений в живом организме во многих случаях происходит так, что за одинаковое время в среднем передается одинаковое количество информации. Понятие информации может быть использовано для количественного описания процессов восприятия и усвоения живыми организмами сигналов разного рода, поступающих к ним из внешнего мира.
Информация относительно опыта β, содержащаяся в опыте α, всегда равна информации относительно α, содержащейся в β:
I (α, β) = H (β) – Hα (β) = H (α) – Hβ (α) = I (β, α)
Равенство информаций I (α, β) и I (β, α) подчеркивается следующей формулой:
I (α, β) = H (α) + H (β) – H (αβ)
Если условная энтропия Hβ (α) равна нулю и, следовательно, информация I (α, β) относительно β, содержащаяся в α, является наибольшей (т.е. ни про какой другой опыт β1 не содержит большей информации об опыте α), то информация относительно любого независимого от β опыта γ, содержащаяся в α, равна нулю — это даст основание говорить, что опыт α «прямо направлен» к выяснению исхода β и не содержит никакой «посторонней» информации. В общем же случае информация относительно любого независимого от β опыта γ, содержащаяся в опыте α, не превосходит величины Hβ (α) = I (α, α) – I (α, β).
При последовательной передаче информации об опыте α, осуществляемой посредством цепочки опытов β, γ, δ, …, где только опыт β непосредственно связан с α, а γ всю содержащуюся в нем информацию об α получает из связи с опытом β (так что βγ уже не содержит об α дополнительной информации по сравнению с β), δ всю информацию об α получает из связи с опытом γ и т.д., информация об α может лишь уменьшаться:
H (α) = I (α, α) ≥ I (β, α) ≥ I (γ, α) ≥ I (δ, α) ≥ …
Наглядной иллюстрацией этого положения может служить известная детская игра в «испорченный телефон».
Глава III. Решение некоторых логических задач с помощью подсчета информации
§ 1. Простейшие примеры
Задача 2. Сколько вопросов надо задать, чтобы отгадать задуманное собеседником целое положительное число, не превосходящее 10, если спрашиваемый на все вопросы отвечает лишь «да» или «нет»?
Опыт β, состоящий в выяснении этого числа, может иметь 10 различных исходов. До ответа на первый поставленный вопрос все эти исходы можно считать равновероятными, так что энтропия H (β) опыта β (т. е. требуемая информация) равна log10 ≈ 3,32 бита. Рассмотрим сложный опыт Ak = α1α2… αk, заключающийся в том, что спрашивающий задает k вопросов. Энтропия опыта α1, заключающегося в постановке одного вопроса, не превосходит одного бита, так как α1, может иметь два исхода (положительный и отрицательный ответы на вопрос); энтропия опыта Ak не превосходит k бит. Для того чтобы исход опыта Ak полностью определял исход β, необходимо, чтобы имело место равенство I (Ak, β) = H (β). Отсюда заключаем, что в этом случае
log 10 = Н (β) = I (Ak, β) ≤ Н (Ak) ≤ k
т.е.
k ≥ log 10 ≈ 3,32,
или, так как k — целое число, k ≥ 4.
Чтобы информация, содержащаяся в ответе на первый вопрос (т.е. энтропия Н (α1)), была возможно большей, т.е. чтобы она действительно равнялась одному биту, надо, чтобы оба исхода нашего опыта α1 были равновероятны. Далее следует потребовать, чтобы информация I (A1, β) относительно β, заключенная в α1, равнялась энтропии Н (α1) опыта α1, а не была бы меньше этой величины. Для этого надо, чтобы ответ на первый вопрос не содержал «посторонней» информации, т.е. чтобы условная энтропия Нβ (α1) равнялась нулю (другими словами: чтобы исход опыта β полностью определял исход α1.
Не нужно, например, интересоваться, может ли число быть больше 10. Эти соображения ясно указывают, как следует поставить первый вопрос. Разобьем множество всех возможных значений х (т.е. множество целых положительных чисел от 1 до 10) на две равные по численности части (так как исходы опыта α1 должны быть равновероятны) и спросим, относится ли х к одной или к другой из них; так, например, можно спросить, будет ли х больше 5. Очевидно, что в этом случае
I (α1, β) = H (β) – Hα1 (β) = 1.
При любом исходе опыта α1, энтропия интересующего нас опыта β уменьшится на 1 бит. Далее следует точно таким же образом разбить новое множество допустимых значений х на две возможно более близкие по численности части и выяснить, к какой из них х принадлежит (если обнаружилось, что х больше 5, то можно спросить, больше ли это число, чем 7).
Альтернативная возможность – записать загаданное число в двоичном виде. Например, число 9 – 101. И спросить, равна ли первая цифра 0, вторая, и т.д.
§ 2. Задачи на определение фальшивых монет с помощью взвешиваний
Задача 3. Имеется 25 монет одного достоинства, 24 из них имеют одинаковый вес, а одна — фальшивая — несколько легче остальных. Спрашивается, сколькими взвешиваниями на чашечных весах без гирь можно обнаружить эту фальшивую монету.
Опыт β, результат которого требуется определить, имеет в этом случае 25 возможных исходов (фальшивой может оказаться любая из 25 монет); эти исходы естественно считать равновероятными, так что H (β) = log 25. Иначе говоря, определение фальшивой монеты в данном случае связано с получением информации, измеряющейся числом log 25. Опыт α1, состоящий в одном (каком угодно) взвешивании, может иметь три исхода (может перевесить левая или правая чашка весов и весы могут остаться в равновесии); поэтому Н (α1) ≤ log 3 и информация I (α1, β), получаемая при проведении такого опыта, не превосходит log 3. Рассмотрим теперь сложный опыт Ak = α1α2… αk, заключающийся в k последовательных взвешиваниях; он дает информацию, не превосходящую k ∙ log 3. Если опыт Ak позволяет полностью определить исход опыта β, то должно быть
Н (Ak) ≥ I (Ak, β) ≥ Н (β) или k ∙ log 3 ≥ log 25
Отсюда заключаем, что 3k ≥ 25, т.е.
или, так как k – целое число, k ≥ 3.
Нетрудно покапать, что с помощью трех взвешиваний всегда можно определить фальшивую монету. Для того чтобы информация, получаемая при проведении опыта α1, была возможно большей, надо, чтобы исходы этого опыта имели возможно более близкие вероятности. Разделим 25 монет на три кучки: 8 + 8 + 9, и положим на весы две кучки по 8 монет. Оставим ту кучку, весы под которой пошли вверх, а в случае равенства, возьмем оставшуюся кучку из 9 монет. Продолжим деление на три кучки, и взвешивание кучек, содержащих равное число монет.
§ 3. Обсуждение
Системы опытов α, приводящие к обнаружению интересующего нас объекта (исхода опыта β), называются вопросниками, а сами опыты α — вопросами; при этом вопросы могут различаться как числом возможных ответов, так и — в ряде случаев — «ценой вопроса», характеризующей затраты, которых требует соответствующий опыт α, или усилия, которые надо приложить для «получения ответа» (т.е. для выяснения исхода α). Задача состоит в том, чтобы отыскать такую процедуру «постановки вопросов» (т.е. такую последовательность опытов α), которая приводит к требуемому ответу (к исходу опыта β) с помощью наименьшей (по числу или по общей «цене») цепочки «вопросов». Фактически требуется наиболее целесообразно использовать ту информацию об исходе опыта β, которая содержится в результатах вспомогательных опытов α.
Если условие равновероятности исходов β не выполняется, следует разбивать множество возможных значений х на две такие части, чтобы вероятности того, что загаданное число принадлежит к одной и к другой из этих частей, были возможно более близки. Такое разбиение обеспечивает наибольшую возможную энтропию опыта α, состоящего в постановке вопроса о том, не принадлежит ли х к одной из этих частей, а следовательно, и наибольшую возможную информацию, содержащуюся в α относительно интересующего пас опыта β. Правда, при этом мы не сможем уже обеспечить минимум наибольшего числа вопросов, которое нам может понадобиться в самом неблагоприятном случае, но зато среднее значение общего числа вопросов здесь будет меньше , чем при любой другой постановке вопросов.
Глава IV. Решение некоторых логических задач с помощью подсчета информации
§ 1. Основные понятия. Экономность кода
Для того чтобы проиллюстрировать пользу введенных в гл. II понятий энтропии и информации, мы разобрали в главе III ряд «занимательных задач» типа тех, которые обычно рассматриваются в школьных математических кружках. В настоящей главе мы рассмотрим некоторые простейшие, но сами по себе достаточно серьезные приложения тех же понятий к практическому вопросу о передаче сообщений по линиям связи.
В технике связи правило, сопоставляющее каждому передаваемому сообщению некоторую комбинацию сигналов, обычно называется кодом, а сама операция перевода сообщения в последовательность различимых сигналов — кодированием сообщения. При этом коды, использующие только два различных элементарных сигнала (на пример, посылку тока и паузу), называются двоичными кодами; коды, использующие три различных элементарных сигнала — троичными кодами и т.д.
В телеграфии, в частности, применяется целый ряд различных кодов, важнейшими из которых являются код Морзе и код Бодо. В коде Морзе каждой букве или цифре сообщения сопоставляется некоторая последовательность кратковременных посылок тока («точек») и в три раза более длинных посылок тока («тире»), разделяемых кратковременными паузами той же длительности, что и «точки»; пробел между буквами (или цифрами) при этом отмечается специальным разделительным знаком — длинном паузой (той же длительности, что и «тире»), а пробел между слонами — еще в 2 раза более длинной паузой.
В настоящее время чаще всего применяется двоичный код Бодо, сопоставляющий каждой букве некоторую последовательность из пяти простейших элементарных сигналов — посылок тока и пауз одинаковой длительности (такой код позволяет не использовать пробелы между словами).
Наиболее экономичный код может быть создан при помощи двоичной системы счисления, в которой число n можно представить и в виде суммы степеней числа 2:
n = bl∙2l + bl-1∙2l-1 + … + b1∙2 + b0
здесь «цифры» bl, bl-1, …, b1, b0 могут принимать лишь значения 1 и 0. В двоичной системе счисления число обозначается последовательностью соответствующих «двоичных цифр»; так, например, поскольку
6 = 1∙22 + 1∙21 + 0∙20, 9 = 1∙23 + 0∙22 + 0∙21 + 1∙20,
то в двоичной системе счисления числа 6 и 9 будут обозначаться, соответственно, как 110 и 1001.
Добавив теперь в начало двоичной записи всех менее чем k-значных чисел некоторое число нулей, мы придем к равномерному двоичному коду для n-буквенного алфавита с минимальной возможной длиной кодовых обозначений. Так, например, при n = 10 соответствующими кодовыми обозначениями будут следующие комбинации, представляющие собой запись в двоичной системе счисления всех чисел от 0 до 9, дополненную, если надо, до четырех знаков нулями в начале: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001.
§2. Коды Шеннона — Фано и Хафмана. Основная теорема о кодировании
Основной результат предыдущего параграфа никак не связан с теоретико-вероятностными рассмотрениями и фактически опирается лишь на элементарный подсчет числа «различных последовательностей из N букв n-буквенного алфавита» и «различных последовательностей из N1 элементарных сигналов». Между тем на практике обычно приходится иметь дело с сообщениями, в которых относительные частоты различных букв значительно отличаются друг от друга (достаточно сравнить, например, частоты букв о и щ в любом русском тексте).
Учет статистических закономерностей сообщения может позволить построить код более экономный, чем наилучший равномерный код, требующий не менее М∙ log n двоичных знаков для записи текста из М букв. Удобно при этом начать с того, что расположить вес имеющиеся n букв в один столбик в порядке убывания вероятностей. Затем все эти буквы следует разбить на две группы — верхнюю и нижнюю — так, чтобы вероятности для буквы сообщения принадлежать к каждой из этих групп были возможно более близки одна к другой; для букв первой группы в качестве первой цифры кодового обозначения используется цифра 1, а для букв второй группы — цифра 0. Далее, каждую из двух полученных групп снова надо разделить на две части и т.д.
Такой метод кодирования сообщений был впервые предложен в 1948–1949 гг. независимо друг от друга Р. Фано и К. Шенноном. Если наш алфавит содержит всего шесть букв, вероятности которых (в порядке убывания) равны 0,4, 0,2, 0,2, 0,1, 0,05 и 0,05, то на первом этапе деления букв на группы мы отщепим лишь одну первую букву (1-я группа), оставив во 2-й группе все остальные. Далее, вторая буква составит 1-ую подгруппу 2-й группы; 2-я же подгруппа той же группы, состоящая из оставшихся четырех букв, будет и далее последовательно делиться на части так, что каждый раз 1-я часть будет состоять из одной лишь буквы (рис. 3).
Рис. 3. Двоичный код для 6-буквенного алфавита
Код Шеннона — Фано является неравномерным. Однако, никакое кодовое обозначение здесь не может оказаться началом другого, более длинного обозначения; поэтому закодированное сообщение всегда может быть однозначно декодировано. Весьма существенно, что буквам, имеющим большую вероятность, в коде Шеннона — Фано соответствуют более короткие кодовые обозначения, чем сравнительно маловероятным буквам. В результате, хотя некоторые кодовые обозначения здесь и могут иметь весьма значительную длину, среднее значение длины такого обозначения все же оказывается лишь немногим большим минимального значения Н, допускаемого соображениями сохранения количества информации при кодировании. Так, для 6-буквенного алфавита наилучший равномерный код состоит из трехзначных кодовых обозначений (ибо 22 < 6 < 23), и потому в нем на каждую букву исходного сообщения приходится ровно 3 элементарных сигнала; при использовании же кода Шеннона — Фано среднее число элементарных сигналов, приходящихся на одну букву сообщения, равно
4∙0,4 + 2∙0,2 + 3∙0,2 + 4∙0,1 + 5∙ (0,05 +0,05) = 2,3.
Это значение заметно меньше, чем 3, и не очень далеко от энтропии
Н = – 0,4∙log 0,4 – 2∙0,2∙log 0,2 – 0,1∙log 0,1 – 2∙0,05∙log 0,05 ≈ 2,22
Достигнутая в рассмотренных выше примерах степень близости среднего числа двоичных знаков, приходящихся на одну букву сообщения, к значению Н может быть еще сколь угодно увеличена при помощи перехода к кодированию все более длинных блоков. Это вытекает из следующего общего утверждения, которое мы будем в дальнейшем называть основной теоремой о кодировании: при кодировании сообщения, разбитого на N-буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близко к Н.
Если использовать не двоичный, а m-ичный код, основанный на m элементарных сигналов, то, по линии связи за единицу времени можно передать L элементарных сигналов (принимающих m различных значений), то скорость передачи сообщений по такой линии не может быть большей, чем
v измеряется в буквах за единицу времени. Величина С = L∙log m зависит лишь от самой линии связи, в то время как Н характеризует передаваемое сообщение. Величина С указывает наибольшее количество единиц информации, которое можно передать по нашей линии за единицу времени (ибо один элементарный сигнал, как мы знаем, может содержать самое большее log m единиц информации). Величина С называется пропускной способностью линии связи.
§ 3. Энтропия и информация конкретных типов сообщений
Письменная речь. Основной результат § 1 этой главы состоял и том, что для передачи M-буквенного сообщения (где М считается достаточно большим) по линии связи, допускающей m различных элементарных сигналов, требуется затратить не меньше чем M log n / log m сигналов, где n — число букв «алфавита», с помощью которого записано сообщение; при этом существуют методы кодирования, позволяющие сколь угодно близко подойти к границе M log n / log m. Так как русский «телеграфный» алфавит содержит 32 буквы (не различаем буквы е и ё, ъ и ъ, но добавляют пробел), то на передачу М-буквенного сообщения надо затратить M log 32 / log m = M Н0 / log m элементарных сигналов. Здесь Н0 = log 32 = 5 — энтропия опыта, заключающегося в приеме одной буквы русского текста (информация, содержащаяся в одной букве), при условии, что все буквы считаются одинаково вероятными.
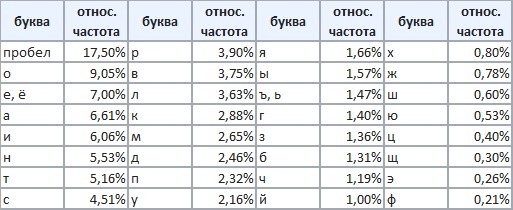
На самом доле, появление в сообщении на русском языке разных букв совсем не одинаково вероятно (рис. 4).
Рис. 4. Относительная частота букв русского алфавита
Приравняй эти чистоты вероятности появления соответствующих букв, получим дли энтропия одной буквы русского текста приближенное значение:
Н1 = Н(α1) = – 0,175∙log 0,175 – 0,09∙log 0,09 – 0,07∙log 0,07 – … – 0,02∙log 0,02 ≈ 4,35
Из сравнения этого значения с величиной Н1= log 32 = 5 бит видно, что неравномерность появления различных букв алфавита приводит к уменьшению информации, содержащейся в одной букве русского текста, примерно на 0,65 бит.
Более того, в осмысленном тексте последовательные буквы вовсе не независимы друг от друга. Наличие в русском языке дополнительных закономерностей приводит к дальнейшему уменьшению степени неопределенности (энтропии) одной буквы русского текста. Но и это еще не всё. Знание двух предшествующих букв еще более уменьшает неопределенность опыта, состоящего в дальнейшем уменьшении Н. В общем случае, с ростом числа N известных предыдущих букв энтропия НN сможет только убывать. НN при N → ∞ стремится к пределу Н∞.
Разность R = 1 – Н∞/H0, показывающую, насколько меньше единицы отношение предельной энтропии Н∞ к величине H0 = log n, характеризующей наибольшую информацию, которая может содержаться в одной букве алфавита с данным числом букв, Шеннон назвал избыточностью языка.
Избыточность русского языка (как и избыточность других европейских языков) заметно превышает 50%. Говоря не совсем точно, мы можем сказать, что выбор следующей буквы осмысленного текста более, чем на 50% определяется самой структурой языка и, следовательно, случаен лишь в сравнительно небольшой степени. Именно избыточность языка позволяет сокращать телеграфный текст за счет отбрасывания некоторых легко отгадываемых слов (предлогов и союзов); она же позволяет легко восстановить истинный текст даже при наличии значительного числа ошибок в телеграмме или описок в книге.
Избыточность R является весьма важной характеристикой языка; однако ее численное значение пока ни для одного языка не определено с удовлетворительной точностью. В отношении русского языка были получены следующие значения (в битах):
Для английского языка Шеннон получил следующий ряд чисел:
Приближенное значение Н(слова) можно вычислить, воспользовавшись законом Ципфа, утверждающим, что при упорядочивании слов языка, в порядке их частот (т.е. вероятностей) частота n-го по порядку слова для всех не слишком больших значений n оказывается примерно пропорциональной 1/n. Этот закон был сформулирован и проверен на большом лингвистическом материале в книге Дж. Ципфа «Поведение человека и принцип наименьшего усилия»; в дальнейшем он многократно обсуждался и уточнялся целым рядом авторов. Так, еще сам Ципф заметил, что в некоторых случаях более точно считать, что частота n-го слова на самом деле пропорциональна 1/na, где постоянная а близка к единице, по все же не равна точно единице (подробнее см. Закон Ципфа и фрактальная природа социальных и экономических явлений). Закон Ципфа широко обсуждается в гл. 5 и 12 книги Джона Пирса Символы, сигналы, шумы.
Заметим, что частоты появления различных букв могут зависеть от характера рассматриваемого текста; точно так же и значения энтропий НN или избыточности R будут различными для текстов, заимствованных из разных источников. При этом любой «специальный язык» (например, научный или технический текст по определенной специальности, деловая переписка, какой-либо жаргон) будет, как правило, иметь избыточность выше средней из-за меньшего количества употребляемых слов и наличии часто повторяющихся специальных терминов и оборотов – весьма благоприятное обстоятельство, очень облегчающее просмотр научной литературы по определенной специальности или чтение такой литературы на недостаточно знакомом языке.
Поэтическая форма (ритм, рифма) накладывает на язык некоторые дополнительные ограничения, т.е. повышает его избыточность. Ориентировочные оценки, проведенные А.Н. Колмогоровым для классического русского четырехстопного ямба (этим стихом написан «Евгений Онегин»), показали, что выполнение требований, накладываемых поэтической формой, снижает неопределенность Н∞ одной буквы текста почти в 2 раза.
Устная речь. В среднем энтропия устной речи несколько выше энтропии письменных текстов, хотя для некоторых типов устной речи (например, для переговоров летчиков с диспетчерами), это будет безусловно не так. Определив среднее число букв, произносимых за единицу времени, можно приближенно оценить количество информации, сообщаемое при разговоре за 1 сек; обычно оно имеет порядок 5–6 бит (это количество информации сильно зависит от скорости разговора).
Однако эта оценка скорости передачи информации при разговоре относится лишь к «смысловой информации». На самом деле живая речь всегда содержит еще довольно значительную дополнительную информацию. Из разговора мы можем судить о настроении говорящего и об его отношении к сказанному; мы можем определить место рождения незнакомого нам человека по его произношению. Количественная оценка всей этой информации представляет собой очень сложную задачу.
Тщательный анализ результатов, касающихся максимальной достижимой скорости разговора, чтения, письма (стенографического) и т.д. показывает, что во всех случаях человек способен усвоить поступающую информацию лишь если скорость ее поступления не превосходит примерно 50 бит/сек.
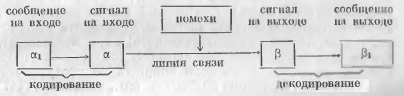
Общая схема передачи по линии связи. Процесс передачи сообщений по произвольной линии связи можно схематически изобразить следующим образом (рис. 5).
Рис. 5. Схема передачи сообщений по линии связи
§ 4. Передача сообщений при наличии помех
Предположим, что последовательные «буквы» сообщения взаимно независимы, причем n букв алфавита характеризуются определенными вероятностями p1, р2, …, рn появления на любом месте сообщения той или иной буквы. Рассмотрим линию связи, в которой для передачи используется m различных элементарных сигналов A1, A2, …, Am, причем за единицу времени может быть передано L таких сигналов (т.е. длительность одного сигнала равна τ = 1/L). Тогда при отсутствии помех сообщение по нашей линии связи можно передавать со скоростью, сколь угодно близкой к величине v = C/H букв/ед. времени, где С = log m – пропускная способность линии связи, а H = –p1 log p1 –p2 log p2 – … –pn log pn – энтропия одной буквы передаваемого сообщения.
При этом для достижения скорости передачи, очень близкой к v, подо лишь разбить передаваемое сообщение на достаточно длинные блоки и воспользоваться кодом, для которого избыточность в закодированном сообщении будет наименьшей.
При наличии помех в линии связи дело будет обстоять несколько иначе. В этом случае только наличие избыточности в передаваемой последовательности сигналов может помочь нам точно восстановить переданное сообщение по принятым данным. Пусть опыт β, состоящий в определении того, какой именно сигнал передастся, будет иметь энтропию Н(β), равную
H (β) = –p(А1)log (А1) –p(А2)log (А2) – … –p(Аm)log (Аm)
Опыт α, состоящий в выяснении того, какой сигнал при этом будет принят на приемном конце, будет, очевидно, опытом с r исходами, зависимым от опыта β; условная вероятность исхода Вj этого нового опыта при условии, что опыт β имел исход Аi (где i = 1, 2, …, m; j = 1, 2, … , r), как раз и равняется pAi(Bj). Средняя информация об опыте р, содержащаяся в опыте α, равна
I (α, β) = Н (β) – Нα (β),
где Нα (β) – условная энтропия опыта β при реализации опыта α. Информация I (α, β) всегда не больше энтропии Н (β) опыта β, т.е. той наибольшей информации об опыте β, которую только можно получить и которая содержится, например, в самом этом опыте. Информация I (α, β) равна энтропии Н (β) только в том случае, когда исход опыта α однозначно определяет исход опыта β, т. е. когда по принятому сигналу всегда можно однозначно выяснить, какой сигнал был передан (с практической точки зрения это означает, что помехи здесь совсем не препятствуют нормальному приему); информация I (α, β) равна нулю в том случае, когда опыт α не зависит от β (т.е. когда принятые сигналы вовсе не зависят от того, какие сигналы передавались – из-за очень сильных помех никакой передачи сообщений фактически вообще не происходит).
Шеннон доказал, что для любой линии связи с помехами всегда можно подобрать специальный код, позволяющий передавать сообщения по этой линии с заданной скоростью, сколь угодно близкой к v = C/H букв/ед. времени, так, чтобы вероятность ошибки в определении каждой переданной буквы оказалось меньше любого заранее заданного числа ε. Это утверждение можно назвать основной теоремой о кодировании при наличии помех. Для этого надо использовать кодирование сразу очень длинных «блоков» из большого числа букв N; поэтому передача сообщений со скоростью, близкой к v, и с очень малой вероятностью ошибки обычно будет сопряжена со значительным запаздыванием при расшифровке каждой переданной буквы.
К сожалению, теорема Шеннона не позволяет указать, как именно надо выбирать кодовые обозначения для того, чтобы сообщения можно было передавать по используемой линии связи с заданной скоростью v1 < v = L∙c/H букв/ед. времени, и притом так, чтобы вероятность ошибки при передаче не превосходила заданного малого числа ε. Из этой теоремы следует лишь, что если разрешить выбирать N сколь угодно большим, то передача со скоростью и вероятностью ошибки, не большей ε, будет возможна.
Так как, однако, при возрастании N существенно возрастает сложность расшифровки кода и увеличивается запаздывание при расшифровке, то для практики небезынтересно уметь оценить также и наименьшее значение вероятности ошибки ε, которое может быть достигнуто при передаче с заданной скоростью v1 с помощью кода, сопоставляющего отдельные кодовые обозначения не более чем N-буквенному блоку.
Отметим, что безошибочная передача информации не может происходить со скоростью v1 > v букв/ед. времени. Для любого фиксированного v1 > v можно найти такое положительное число q0 > 0 (которое, видимо, должно зависни, от v1, и при увеличении v1 возрастать), что в случае передачи информации по линии связи со скоростью v1 вероятность ошибки q при расшифровке каждой переданной буквы сообщения при любом методе кодирования и декодирования будет не меньше, чем q0.
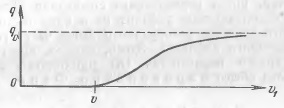
Схематически график зависимости нижней границы q0 вероятности ошибки от скорости передачи v1 изображен на рис. 6. То обстоятельство, что при v1 < v этот график совпадает с осью абсцисс (т.е. q0 = 0), очевидно, соответствует основной теореме Шеннона о кодировании.
Рис. 6. Зависимость вероятности ошибки декодирования q от скорости передачи информации v
§ 5. Коды, обнаруживающие и исправляющие ошибки
Ограничимся простейшими двоичными линиями связи, т.е. будем считать, что по линии можно передавать только два элементарных сигнала (скажем, посылку тока и паузу) и что эти же два сигнала могут быть приняты на приемном конце линии. Будем обозначать используемые сигналы цифрами 0 и 1; в таком случае все кодовые обозначения будут последовательностями этих цифр, т.е. числами, записанными в двоичной системе счисления.
Рассмотрим, например, случай, когда N = 3, а число используемых кодовых обозначений равно двум. В качество кодовых обозначений разумно выбрать тройки 000 и 111; такой выбор с точки зрения использования проверок на четность можно обосновать следующим образом. Сопоставим два кодовых обозначения двум возможным значениям первого элементарного сигнала а0 (т. е. будем считать, что только сигнал а0 реально содержит информацию), а далее условимся вслед за каждым информационным сигналом а0 передавать еще два «контрольных сигнала» а1 и а2, подобранных так, чтобы суммы а0 + а1 и а0 + а2 обе были четными (реально это как раз и сведется к выбору в качестве кодовых обозначений цепочек 000 и 111).
Если при приеме тройки сигналов не произошло сразу двух или трех ошибок (т.е. если считать возможными лишь правильную передачу и передачу с одиночными ошибками), то, проверив четность сумм а’0 + а’1 и а’0 + а’2 в принятой на приемном конце тройке а’0, а’1, а’2, можно будет безошибочно установить, какая же именно тройка была на самом деле передана.
В самом деле, если обе суммы а’0 + а’1 и а’0 + а’2 окажутся четными, то отсюда сразу будет следовать, что ошибок при передаче не было (напомним, что что возможность двойной ошибки мы исключаем); если нечетной будет лишь одна из них, то это будет значить, что ошибочно принят входящий в эту сумму контрольный сигнал а1 или а2, а если обе суммы а’0 + а’1 и а’0 + а’2 — нечетные, то это значит, что неверно принят информационный сигнал а0. Таким образом, ценой уменьшения скорости передачи втрое (по сравнению с максимальной скоростью L бит/ед. времени) мы можем добиться того, чтобы все одиночные ошибки в тройках элементарных сигналов были исправлены.
Сочинения по теории информации и по кибернетике
К. Шеннон. Математическая теория связи, в книге: «Работы по теории информации и кибернетике», М., ИЛ, 1963, стр. 243—332. [В этой книге, рассчитанной, в первую очередь, на специалистов, собраны все основные работы К. Шеннона по теории информации и теории кодирования.]
Л. Бриллюэн. Наука и теория информации, М., Физматгиз, 1959.
Дж. Пирс. Символы, сигналы, шумы, М., «Мир», 1967.
К. Черри. Человек и информация, М., «Связь», 1972.
А. Файнстейн. Основы теории информации, М., ИЛ, 1960.
Р. Фано. Передача информации. Статистическая теория связи, М., «Мир», 1965.
А. Н. Колмогоров. Теория передачи информации, в книге: «Сессия Академии наук СССР по научным проблемам автоматизации производства 15—20 октября 1956 г.; пленарные заседания», М., Изд-во АН СССР, 1957.
Н. Винер. Кибернетика, М., «Советское радио», 1968.
У. Р. Эшби. Введение в кибернетику, М., ИЛ, 1958.
А. Моль. Теория информации и эстетическое восприятие, М., «Мир», 1966.
А. Н. Колмогоров. Три подхода к определению понятия «количество информации», Пробл. передачи информ. 1, № 1, 1965, стр. 3–11; К логическим основам теории информации и теории вероятностей, Пробл. передачи информ. 5, № 3, 1969, стр. 3–7.