В предыдущей заметке мы рассмотрели понятия математического ожидания, дисперсии и стандартного отклонения дискретной случайной величины. В настоящей заметке вводится понятие ковариации между двумя переменными и его применение для управления портфелем активов. Эта задача вызывает большой интерес у финансовых аналитиков. [1]
Ковариация σXY между двумя дискретными случайными величинами X и Y определяется формулой
где Xi — i-e значение дискретной случайной величины X, Р(Хi) — вероятность i-гo значения дискретной случайной величины X, Yi — i-e значение дискретной случайной величины Y, Р(Yi) — вероятность i-гo значения дискретной случайной величины Y, Р(ХiYi) — вероятность i-гo значения дискретной случайной величины X и i-гo значения дискретной случайной величины Y, i = 1, 2, … , N.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Например, представьте, что вам предстоит сделать одну из двух альтернативных инвестиций. Первая инвестиция представляет собой вложение средств во взаимный фонд, владеющий различными акциями, определяющими индекс Доу-Джонса. Назовем его фондом Доу-Джонса. Вторая инвестиция — приобретение акций взаимного фонда, приносящих наибольшую доходность во время экономического спада. Присвоим ему название фонд экономического спада. Вы оцениваете доходность каждой инвестиции (прибыль на 1000 долл.) для каждого из трех возможных вариантов состояния экономики, имеющих определенную вероятность, и заполняете табл. 1.
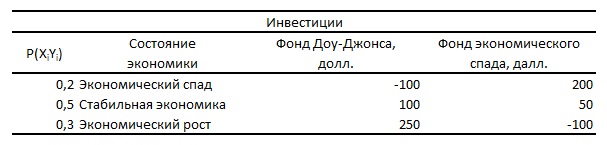
Таблица 1. Прогнозируемая прибыль от каждой инвестиции для каждого из трех возможных вариантов состояния экономики
Математическое ожидание и стандартное отклонение доходности каждой инвестиции, а также ковариация между их показателями доходности вычисляются следующим образом. Пусть X— доходность фонда Доу-Джонса, Y— доходность фонда экономического спада.
Таким образом, математическое ожидание доходности фонда Доу-Джонса выше, чем у фонда экономического спада. Однако стандартное отклонение фонда Доу-Джонса также превышает стандартное отклонение фонда экономического спада, что говорит о более высокой степени риска. Ковариация между показателями доходности обоих фондов, равная –12 675, свидетельствует о сильной обратной зависимости. Иначе говоря, доходность обоих фондов изменяется в противоположных направлениях. Если доходность одного из фондов возрастает, доходность другого снижается.
Вычислив ковариацию между двумя случайными переменными X и Y, можно определить математическое ожидание, дисперсию и стандартное отклонение их суммы. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий каждой величины:
(2) E(X+Y) = Е(Х) + E(Y)
Дисперсия суммы двух случайных величин равна сумме дисперсий каждой величины и удвоенной ковариации между ними.
Стандартное отклонение суммы двух случайных величин равно квадратному корню из дисперсии:
Проиллюстрируем вычисление математического ожидания, дисперсии и стандартного отклонения суммы двух случайных величин на примере двух инвестиционных фондов, описанных выше. Обозначим через X — доходность фонда Доу-Джонса, а через Y — доходность фонда экономического спада.
Математическое ожидание суммы прибылей фонда Доу-Джонса и фонда экономического спада равно 140 долл., а стандартное отклонение равно 20 долл. Обратите внимание на то, что стандартное отклонение суммы прибылей, которые могут быть получены в результате двух инвестиций, намного меньше, чем стандартное отклонение доходности каждой инвестиции в отдельности. Это объясняется большой отрицательной ковариацией, существующей между показателями доходности этих фондов.
Ковариация, математическое ожидание и стандартное отклонение суммы двух случайных величин позволяют оценить доходность и риск портфельных инвестиций. Диверсифицируя свои вклады, инвесторы приобретают разные ценные бумаги, стремясь получить максимум прибыли при минимальном риске. При исследовании доходности портфелей ценных бумаг каждому пакету акций присваивают определенный вес. Это позволяет оценить ожидаемую доходность портфеля акций и его риск.
Ожидаемая доходность портфеля ценных бумаг, состоящего из двух пакетов акций:
(5) Е(Р) = wE(X) + (1 – w)E(Y)
где Е(Р) — ожидаемая доходность портфеля, Е(Х) — ожидаемая доходность пакета акций X, E(Y) — ожидаемая доходность пакета акций Y, w — доля пакета акций X в портфеле ценных бумаг, (1 – w) — доля пакета акций Y в портфеле ценных бумаг.
Риск портфеля ценных бумаг:
В предыдущем примере мы оценили математическое ожидание и стандартное отклонение инвестиций в фонд Доу-Джонса и фонд экономического спада, а также ковариацию между ними. Допустим, что портфель активов состоит из пакетов акций двух фондов стоимостью по 500 долл. каждый. Вычислим ожидаемую доходность и риск такого портфеля акций, используя формулы (5) и (6):
Таким образом, ожидаемая доходность портфеля составляет 70 долл. на каждую тысячу вложенных долларов (доходность равна 7%), а риск портфельных инвестиций равен 10 долл. Обратите внимание на то, что такой небольшой риск объясняется большой отрицательной ковариацией между двумя инвестициями. То, что инвестиции приносят максимальную прибыль в разных экономических ситуациях, позволяет минимизировать общий риск.
Предыдущая заметка Распределение дискретной случайной величины
Следующая заметка Биномиальное распределение
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 300–303
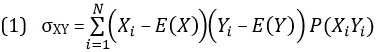


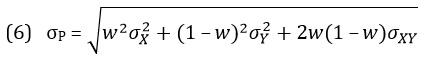
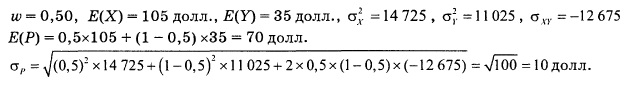
В первой формуле после E(x) не закрыта еще одна скобка.
Статья хорошая, спасибо!
Олег, спасибо. Поправил.
Не правильный расчет!
У ва с Var x = 14.725. (что есть сигма в квадрате)
а потом ско равно вдруг 121??????
Поправил. В результате расчета 14,725 была лишняя запятая. Правильно 14 725. При переводе книги с английского не убрали разделитель разрядов, принятый в англоязычной среде — запятая разделяет по три разряда. В русском варианте используется пробел.