Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью

Тема закономерного и случайного мне очень интересна. В частности из-за тех решений, которые я наблюдаю в корпоративной, да и в обычной жизни. Многие события происходят в точности с афоризмом: «наказание невиновных, награждение непричастных». На мой взгляд, роль случая очень любопытно раскрыта в работах Нассима Талеба Одураченные случайностью, Черный лебедь, О секретах устойчивости. Поэтому, когда я увидел книжку Млодинова, то немедленно приобрел ее, предвкушая несколько часов интереснейшего чтива. И не прогадал. Лично мне книга очень понравилась. Не уверен, правда, что многие со мной согласятся… 🙂

Эта книга – отличный способ тряхнуть стариной и освежить в памяти кое-что из курса высшей математики, истории естественнонаучного знания, астрономии и статистики для тех, кто изучал эти дисциплины в вузах; понятно и доступно изложенные основы теории вероятностей и ее применимости в житейских обстоятельствах для тех, кому не посчастливилось изучать их специально; наконец, профессиональный и дружелюбный подсказчик, грызущим гранит наук в данный момент.

Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью. М.: Livebook/Гаятри, 2010. – 352с.

Скачать краткий конспект в формате Word

Глава 1. Под лупой случайности

В 2002 г. лауреатом Нобелевской премии по экономике стал ученый Дэниэл Канеман. В середине 1960-х гг. Канеман, тогда еще младший преподаватель психологии в Еврейском университете, согласился выполнить довольно-таки скучную работу: прочитать инструкторам израильских ВВС лекцию по общепринятой точке зрения на модификацию поведения применительно к психологии обучения полетам. Канеман доказывал, что поощрение примерного поведения имеет смысл, а наказание за ошибки – нет. Один из слушавших прервал Канемана и высказал свое мнение: «Частенько я расхваливал пилотов за идеально выполненные маневры, и что вы думаете? В следующий раз у них выходило гораздо хуже, – сказал инструктор. – На тех, кто выполнял маневры плохо, я кричал – на следующий день у них получалось гораздо лучше. Так что не надо рассказывать мне сказки о том, будто поощрение способствует повышению качества работы, а наказание – нет. По своему опыту знаю, что это не так». Другие инструкторы согласились с ним. Канеману слова инструктора показались не лишенными смысла. В то же время Канеман доверял результатам опытов над животными, которые свидетельствовали: поощрением можно добиться большего, нежели наказанием. Он стал размышлять над этим явным парадоксом. И тут его осенило: крик предшествовал наказанию, однако, несмотря на очевидное, не обуславливал его.

Как такое возможно? Ответом на этот вопрос служит феномен «регрессии к среднем». Суть в том, что в любом ряду случайных событий за событием из ряда вон выходящим скорее всего и по чистой случайности последует событие ординарное. Механизм таков. Каждый пилот в той или иной степени обладает навыком управления самолетом-истребителем. Совершенствование этого навыка зависит от многих факторов, в том числе и от длительных тренировок. Таким образом, хотя в процессе тренировок мастерство пилотов медленно растет, за один полет многого они не добьются. И любой особенно удачный или неудачный полет будет зависеть в большой степени от везения. Так что если пилот посадил машину идеально, что называется, прыгнул выше своей головы, велика вероятность, что следующий полет у него пройдет на уровне гораздо ближе к его личной норме, то есть неважно. Если инструктор после первого полета своего подопечного хвалил, результаты следующего вылета докажут, что похвала будто бы не пошла на пользу.

Тверский и Канеман выяснили: когда речь заходит о случайных процессах убеждения, интуиция людей часто подводят. [1]

Часто случается, что невероятно успешные авторы поначалу получают отказ за отказом. Например, не так уж много книг, которые сегодня во всем мире имели бы большую популярность, чем книги Джона Гришема или Джоан Роулинг. И чем не менее, их рукописи в ту пору, когда сами авторы еще не прославились, раз за разом отвергали. Рукопись Гришема «Пора убивать» отклонили двадцать шесть издательств, его вторая рукопись, «Фирма», заинтересовала издателей только после того, как неофициальный экземпляр романа, ходивший по рукам в Голливуде, привлек внимание кинематографистов, предложивших за права на экранизацию 600 тыс. долларов. Джоан Роулинг с ее первым романом о Гарри Поттере получила девять отказов. Существует и оборотная сторона медали, хорошо известная любому человеку, связанному с миром бизнеса: многие талантливые писатели – эти Джоны Гришемы, бросившие попытки после двадцатого отказа, Джоан Роулинг, прекратившие борьбу после пяти отрицательных ответов – так и не пробились. После многочисленных отказов один такой писатель, Джон Кеннеди Тул, потерял надежду когда-нибудь опубликовать свой роман и покончил с собой. Его мать не оставила попыток, и одиннадцать лег спустя «Сговор остолопов» был опубликован. Он завоевал Пулитцеровскую премию, разойдясь тиражом в 2 млн. экземпляров.

В мире политики, экономики, бизнеса – даже если на кону миллионы долларов – случайные события часто истолковываются в неверном ключе: как достижения или провалы. Заслужены ли поощрения (и наказания) в голливудской игре, играет ли удача в случае с огромными (или скудными) кассовыми сборами куда как большую роль, чем это кажется? Все мы понимаем: один только факт гениальности еще не гарантирует успеха, однако сам собой напрашивается вывод: успех всегда гениален. Уильям Голдман в своей ставшей классической книге 1983 г. «Приключения в кинематографическом бизнесе» повторяет слова бывшего продюсера Дэвида Пикера: «Если бы я сказал «да» всем проектам, которые отверг, и «нет» всем тем, которые принял, итог оказался бы примерно таким же, что и сейчас». Тем не менее, руководство студии судят не за управленческие способности, основу всех основ, которыми в равной степени должны обладать и глава американской сталелитейной компании, и глава «Парамаунт Пикчерз». Наоборот, его ценят за умение выбирать из множества сценариев будущие хиты. И если Голдман прав, то умение это не более чем иллюзия, и как бы глава студии ни пыжился, его заслуга в подписании контракта на 25 млн. долларов невелика.

Когда мы рассматриваем невероятный успех, будь то в спорте или где еще, необходимо помнить о следующем: необычные события могут происходить без необычных тому причин. Случайные события часто выглядят как неслучайные, и, истолковывая все, что связано с человеком, нужно быть осторожным – не спутать одно с другим.

Глава 2. Законы правды и полуправды

Чего в английском языке больше: слов из шести букв, пятая из которых n, или слов из шести букв, имеющих окончание -ing? Большинство считают, что слов с окончанием -ing больше. Но почему? Потому что такие слова быстрее приходят на ум. Психологи называют подобный тип ошибок тенденцией оценивать вероятность по наличию примеров: реконструируя прошлое, мы отдаем ничем не оправданное предпочтение тем воспоминаниям, которые отличаются наибольшей живостью и, следовательно, быстрее всплывают в памяти.

Использование математических выкладок в современной правовой системе сопряжено со значительными затруднениями. Одним из наиболее известных дел, служащих примером правильного и неправильного применения вероятности в юриспруденции, является дело «Штат против Коллинзов», слушания по которому проходили в 1968 г. в калифорнийском Верховном суде. Вот выдержка из судебного решения:

«18 июня 1964 г. около 11:30 миссис Хуанита Брукс, совершавшая покупки, шла вдоль переулка в Сан-Педро, г. Лос-Анджелес. За собой она катила тележку с плетеной корзиной, в которой лежали продукты, а поверх – кошелек. Миссис Брукс опиралась на трость. Когда она наклонилась, чтобы поднять пустую коробку, ее внезапно сбил человек – она не видела и не слышала его приближения. После падения миссис Брукс не сразу пришла в себя – она больно ударилась. Подняв голову, миссис Брукс успела заметить убегавшую молодую женщину. По словам миссис Брукс, женщина была среднего сложения, одета «во что-то темное», а о цвете волос миссис Брукс отозвалась как о «чем-то среднем между русым и светлой блондинкой», но светлее, чем волосы обвиняемой Джанет Коллинз, как выяснилось во время суда. Сразу после случившегося миссис Брукс обнаружила, что исчез ее кошелек, в котором было долларов 35 или 40.

Примерно в то же самое время, как произошло ограбление, Джон Басс, живущий в том же переулке, только в самом конце, поливал газон перед домом. Его внимание привлекли «плач и крики». Он повернулся на звуки и увидел, как из переулка выбегает женщина и садится в желтую машину через дорогу. Машину тут же завели; она рванула, на скорости объезжая другую машину, и при этом проехала совсем рядом с Бассом. Басс заметил, что за рулем сидел негр с усами и бородой… Другие свидетели описывали машину как желтую, желтую с кремово-белым верхом, желтую с верхом цвета яичной скорлупы. О самой машине отзывались как о большой либо средних размеров».

Через несколько дней после ограбления лос-анджелесский полицейский заметил желтый «линкольн» с кремово-белым верхом – машина стояла у дома обвиняемых. Полицейский вступил с ними в разговор, объясняя, что расследует ограбление. Он отметил, что внешность подозреваемых соответствовала описанию свидетелей, за исключением бороды у мужчины, впрочем, мужчина сказал, что раньше носил бороду. В тот же день, только позднее, полиция арестовала подозреваемых, ими оказались Малькольм Рикардо Коллинз и его жена Джанет.

Улик против подозреваемой пары было недостаточно, и дело строилось в основном на их опознании жертвой и свидетелем, Джоном Бассом. К несчастью для обвиняющей стороны, ни миссис Брукс, ни Джон Басс не годились в качестве главных свидетелей. Миссис Брукс не могла опознать Джейн как исполнителя преступления, а водителя машины вообще не видела. Джон Басс не видел саму преступницу, а из нескольких лиц, предъявленных к опознанию, не смог с уверенностью показать водителя. Казалось, дело разваливается.

И тут появляется главный свидетель, который в бумагах суда записан всего лишь как «учитель математики из государственного колледжа». Этот свидетель сделал заявление: факта того, что обвиняемые были «белой женщиной со светлыми волосами, завязанными в хвост… [и] негром с бородой и усами», который сидел за рулем частично желтой машины, достаточно для признания пары виновной. Чтобы наглядно доказать свое утверждение, обвиняющая сторона представила следующую таблицу, слово в слово приведенную из решения суда:

Характерная особенность	Вероятность одного события
частично желтая машина	1/10
мужчина с усами	1/4
негр с бородой	1/10
женщина с волосами, завязанными в хвост	1/10
женщина со светлыми волосами	1/3
мужчина и женщина разной расовой принадлежности в машине	1/1000

Учитель математики, выступавший со стороны обвинения, сказал, что к этим данным применимо правило умножения вероятностей. Умножая все вероятности, можно прийти к выводу, что шанс Коллинзов на соответствие всем этим четким характеристикам равен 1 из 12 млн. Соответственно, по словам обвинителя, можно заключить, что вероятность Коллинзов оказаться невиновными равна 1 из 12 млн. Затем обвинитель отметил, что эти отдельные вероятности являются оценочными показателями, и предложил присяжным высказать свои собственные догадки, а затем перейти к математическим подсчетам. Сам он, продолжал обвинитель, полагает, что показатели достаточно скромные; у него вероятность с учетом факторов приближается к 1 из млрд. Присяжные согласились и вынесли обвинительный приговор.

Что здесь не так? Во-первых, чтобы получить суммарную вероятность путем умножения отдельных вероятностей, эти отдельные вероятности должны быть независимыми друг от друга, а в данном случае это явно не так. К примеру, в таблице вероятность «негра с бородой» равна 1 из 10, а «мужчины с усами» – 1 из 4. Но большинство бородатых мужчин носят и усы, поэтому если был замечен «негр с бородой», вероятность того, что у наблюдаемого мужчины есть усы, уже не равна 1 из 4, она гораздо выше. Это несоответствие может быть устранено, если убрать категорию «негр с бородой». В таком случае согласно правилу умножения вероятностей получится 1 из 1 млн.

Однако в анализе допущена и другая ошибка: вероятность, указанная выше, – что произвольно выбранная пара совпадет по описанию с описанием подозреваемых — не является искомой вероятностью. Скорее, это вероятность того, что пара, отвечающая всем приведенным характеристикам, является виновной. Первая вероятность может быть равной 1 из 1 млн. Что до второй, то при условии, что население района, прилегающего к району совершения преступления, составляет несколько миллионов, можно с достаточным основанием говорить о 2–3 парах, соответствующих описанию. В таком случае вероятность того, что пара, отвечающая описанию, виновна, основывается на одном только этом доказательстве (в принципе, единственном, имевшемся в распоряжении обвинения) и равна всего 1 из 2 или 1 из 3. И где здесь отсутствие обоснованного сомнения? В результате Верховный суд отменил решение об обвинительном приговоре.

Глава 3. Продираясь через дебри вероятностей

Если верить газетным публикациям, рубрика «Спросите Мэрилин» журнала «Парад» была просто-напросто обречена на феноменальный успех. Наибольшая популярность Мэрилин связана с ответом на следующий вопрос по викторине Монти Холла: «Предположим, участники телевикторины должны выбрать одну из трех дверей. За одной дверью находится машина, за двумя другими – по козе. Участник выбирает дверь, а ведущий, которому известно, что находится за каждой из дверей, открывает одну из оставшихся, за которой коза. Затем он говорит участнику: «Итак, вы смените дверь или останетесь на месте?» Вопрос в следующем: выгодно ли участнику сменить дверь?

Мэрилин в своей колонке ответила: имеет смысл сменить дверь. 92% американцев заявили о том, что Мэрилин ошиблась. «Какая чушь!», писал один математик из Университета Джорджа Мейсона: «Поясняю: Если за одной из трех дверей машины не оказалось, то вероятность выигрыша при оставшихся двух дверях меняется и равна 1/2, причем ни один из вариантов не имеет бо́льшую вероятность. Как математик я очень огорчен общим низким уровнем математических способностей населения. Поэтому призываю вас помочь повысить этот уровень, признав свою ошибку, и впредь быть более аккуратной».

Для решения задачи не требуется знаний ни численных методов, ни геометрии с алгеброй. Требуется лишь общее понимание принципа действия вероятности, а также закона пространства элементарных событий, необходимого для анализа ситуации с вероятностями, который впервые был записан в XVI в. и автор которого – Джероламо Кардано. В своем «Трактате об азартных играх» Кардано касается и карточных игр, и костей, и нард, и даже игры в «бабки». Метод, с помощью которого Кардано энергично взялся за решение вопросов вероятности, удивительно действенный и в то же время простой. В главе 14 «Об общих точках» Кардано выводит, по его словам, «общее правило» – наш закон пространства элементарных событий. На современном языке правило Кардано звучит следующим образом: «Предположим, случайный процесс имеет множество одинаково вероятных исходов: некоторые из них благоприятны (то есть ведут к выигрышу), некоторые неблагоприятны (то есть проигрышные). Вероятность благоприятного исхода равна доле благоприятных исходов. Множество всех возможных исходов образует пространство элементарных событий». Другими словами, брошенный кубик опускается на любую из шести своих сторон, и эти шесть исходов формируют пространство элементарных событий. Если вы ставите пари на, скажем, два из них, ваши шансы выиграть равны 2 из 6.

В задаче Монти Холла фигурируют три двери: за одной нечто ценное, скажем, шикарная красная «мазерати», за двумя другими – нечто гораздо менее интересное, скажем, полное собрание сочинений Шекспира на сербском. Вы выбрали дверь 1. В таком случае пространство элементарных событий представлено следующими тремя возможными исходами:

«Мазерати» за дверью 1
«Мазерати» за дверью 2
«Мазерати» за дверью 3

Вероятность каждого исхода – 1 из 3, то есть шансы угадать равны 1 из 3.

Ведущий, заведомо знающий, что находится за каждой из дверей, открывает одну дверь из не выбранных вами, и оказывается, что за дверью собрание сочинений Шекспира. Поскольку, открывая эту дверь, ведущий использовал свое знание о предметах за дверями, чтобы не раскрыть местонахождение «мазерати», данный процесс нельзя назвать случайным в прямом смысле этого слова. Существуют два варианта, которые стоит обдумать.

Первый – вы изначально делаете правильный выбор. Назовем такой случай «счастливой догадкой». Ведущий наугад откроет либо дверь 2, либо дверь 3, и если вы предпочтете сменить свою дверь, вы проиграете. В случае «счастливой догадки» лучше, конечно, не соблазняться предложением сменить дверь, однако вероятность выпадения «счастливой догадки» равна всего лишь 1 из 3.

Второй – вы в первый раз указываете не на ту дверь. Назовем такой случай «ошибочной догадкой». Шансы, что вы не угадаете, равны 2 из 3, так что «ошибочная погадка» в два раза вероятнее, чем «счастливая догадка». Как «ошибочная догадка» отличается от «счастливой догадки»? При «ошибочной догадке» «мазерати» находится за одной из тех дверей, которые вы обошли своим вниманием. В противоположность «счастливой догадке» в этом варианте ведущий открывает невыбранную дверь не наугад. Поскольку он не собирается открывать дверь с «мазерати», он выбирает ту самую дверь, за которой машины нет. Другими словами, в «ошибочной догадке» ведущий вмешивается в то, что до той поры называлось случайным процессом. Таким образом, процесс уже не может считаться случайным: ведущий пользуется своими знаниями, чтобы повлиять на результат, и тем самым отрицает само понятие случайности, гарантируя, что при смене двери участник получит это шикарное авто. Из-за подобного вмешательства происходит следующее: вы оказываетесь в ситуации «ошибочной догадки», и, следовательно, выигрываете при смене двери и проигрываете, если отказываетесь сменить ее.

В итоге получается: если вы оказываетесь в ситуации «счастливой догадки» (вероятность которой 1/3), вы выигрываете при условии, если остаетесь при своем выборе. Если вы оказываетесь в ситуации «ошибочной догадки» (вероятность которой 2/3), то под влиянием действий ведущего вы выигрываете при условии, если меняете первоначальный выбор. Шансы того, что вы попали в ситуацию «ошибочной догадки», равны 2 к 1, так что лучше сменить дверь. Вот и статистика телепередачи подтверждает: те, кто оказывался в подобной ситуации и изменял свое первоначальное решение, выигрывали примерно в два раза чаще, чем те, кто стоял на своем. (Любопытно, что описанный подход широко используется в карточной игре бридж. Там он известен как Принцип ограниченного выбора. — Прим. Багузина)

Глава 4. Прокладывая путь к успеху

Галилео Галилей написал небольшую работу об азартных играх: «Размышления на тему игры в кости». Работа была напечатана по заказу покровителя Галилео, герцога Тосканского. Герцога интересовал вопрос: почему при броске трех костей чаще выпадает 10, чем 9? Собственно говоря, а почему 10 должна выпадать чаще, чем 9? И 10, и 9 можно представить 6 способами, в зависимости от того, как упадут три кубика. Для 9: (621), (531), (522), (441), (432) и (333). Для 10 это (631), (622), (541), (532), (442) и (433). Применяя закон Кардано о пространстве элементарных событий, получаем: вероятность благоприятного исхода равна соотношению исходов, которые благоприятны. Сумма 9 и 10 может быть составлена теми же 6 способами. Тогда почему одно вероятнее другого?

А потому, что закон пространства элементарных событий применим только к тем исходам, которые обладают равной вероятностью. Вышеприведенные же комбинации таковыми не являются. К примеру, исход (631), то есть бросок, в результате которого выпадают 6,3 и 1, в 6 раз более вероятен по сравнению с исходом (333), поскольку, хотя и существует один способ, в результате которого выпадают три 3, способов, в результате которых получаются 6, 3 и 1, целых шесть: можно получить 6, затем 3 и 1, или же сначала 1, затем 3, а потом уже 6, ну и так далее. Представим запись исхода, где порядок бросков записывается трехзначными, разделенными запятой комбинациями. Тогда все то, что мы только что сказали, можно выразить короче: исход (631) состоит из возможностей (1,3,6), (1,6,3), (3,1,6), (3,6,1), (6,1,3) и (6,3,1), а исход (333) состоит только лишь из (3,3,3). Как только мы упростили запись таким образом, стало понятно: исходы одинаково вероятны, и можно применить закон. Поскольку существует 27 способов получить общую сумму в 10, бросая три кости, но лишь 25 способов получить сумму в 9, Галилей заключил: при броске трех костей вероятность выпадения 10 в 27/25 раз больше, чем выпадения 9.

Решая поставленный перед ним вопрос, Галилей косвенным образом применил следующий важный принцип: «Вероятность события зависит от числа его исходов».

Научная революция разворачивалась, и границы теории случайности ширились от Италии к Франции, где ученые нового типа, подвергавшие сомнению Аристотеля и следовавшие Галилею, совершали еще более глубокие открытия, нежели Кардано или сам Галилей. Одним из них был Блез Паскаль.

В 1654 году шевалье де Мере обратился к Паскалю с просьбой помочь. Предположим, вы с партнером играете, у вас равные шансы, и тот, кто первым наберет определенное количество очков, выигрывает. Игра прерывается; в это самое время один из игроков лидирует. Как справедливее всего разделить сумму? При разрешении этой проблемы, заметил де Мере, нужно учесть шансы каждого игрока на выигрыш исходя из того, у кого этих шансов на момент прерывания игры больше.

Обратимся к современному примеру. В 1996 г. команда «Смельчаки Атланты» победила «Нью-Йоркских Янки» в первых 2 играх бейсбольной Мировой серии (по условиям первая команда, победившая в 4 играх, становится чемпионом). Факт победы «Смельчаков» в первых 2 играх совсем не обязательно означал, что ее игроки сильнее. Предположим, что и та, и другая команды обладали равными шансами на победу в каждой игре, и что в первых 2 играх лишь по случайности выиграла команда «Смельчаки Атланты». Основываясь на этом предположении, зададимся вопросом: каковы были шансы «Янки» победить? Чтобы вычислить это, мы подсчитываем все возможности для «Янки» выиграть серию и сравниваем их с количеством возможностей проиграть. 2 игры из серии уже были сыграны, оставалось сыграть еще 5 игр. Каждая игра содержала в себе 2 возможных исхода: «Янки» выигрывают (Y) или «Смельчаки» выигрывают (В). Всего исходов 2⁵ = 32. К примеру, «Янки» могли бы выиграть 3 игры, а следующие 2 проиграть: YYYBB; либо они могли выигрывать и проигрывать через раз: YBYBY. (В последнем случае, поскольку «Смельчаки» имели бы 4 победы после 6 игр, последняя игра вообще не состоялась бы, однако к этому моменту мы еще вернемся). Вероятность того, что «Янки» еще смогут выиграть в Мировой серии, была равна числу исходов с хотя бы 4 выигранными играми, разделенному на общее число исходов – 32; вероятность того, что «Смельчаки» выиграли бы, была равна числу исходов с хотя бы еще 2 выигрышами, также разделенному на 32.

Такой подсчет выглядит странным, поскольку, как я уже заметил, включает варианты (как, например, YBYBY), при которых команды продолжают играть даже после того, как «Смельчаки» одерживают необходимые им 4 победы. Раз «Смельчаки» выигрывают 4 игры, 7-ю игру команды, конечно же не играют. Однако математика не зависит от человеческих причуд, и неважно, играют команды или не играют, это никак не отражается на факте существования таких исходов. Таким образом, мы просто-напросто учитываем возможную последовательность из 5 игр, которые еще предстоит сыграть. «Янки» стали бы победителями в том случае, если бы выиграли 4 из 5 возможных оставшихся игр: BYYYY, YBYYY, YYBYY, YYYBY, YYYYB или все 5: YYYYY. То есть, шансы «Янки» на победу равны 6 из 32, или около 19%. Если состязание в рамках Мировой серии вдруг остановили бы, то, согласно Паскалю, именно таким образом следовало бы распределить призовое вознаграждение, и именно такими были бы шансы на победу при условии заключения пари после первых 2 игр. Кстати, «Янки» все же вернули себе преимущество – выиграли следующие 4 игры, – и стали чемпионами.

Главное достижение Паскаля заключается в том, что он применил систематический подход к подсчету, позволяющий получить ответ путем расчетов по формуле или вывести его из табличных значений. Подход основан на любопытном расположении чисел – в форме треугольника (рис. 1).

Рис. 1. Треугольник Паскаля (http://www-formula.ru/index.php/pascal-triangle)

Треугольник Паскаля пригодится всякий раз, когда нужно выяснить количество способов, посредством которых находится некоторое число предметов из общего числа, равного выбираемому числу или превосходящее его (число комбинаций).

В случае задачи, где «Янки» и «Смельчаки» боролись за победу в Мировой серии, мы производили подсчеты всех возможных ситуаций для 5 оставшихся игр. Теперь же узнать число способов, какими «Янки» могут выиграть 0, 1, 2, 3, 4 или 5 игр, можно прямо из пятого ряда треугольника:

Видно, что шанс «Янки» выиграть 2 игры (10 способов) в два раза больше, чем шанс выиграть 1 игру (5 способов). Вариантов же одержать победу в серии 6: сумма последней и предпоследней ячеек в ряду.

Паскаль подробно изложил анализ «за» и «против» моральных обязательств человека перед Богом. Новаторство было в методе Паскаля, с помощью которого уравнивались «за» и «против» – в наше время это понятие называется математическим ожиданием. Чтобы сравнить возможные выгоды и потери. Паскаль предложил умножить вероятность каждого возможного исхода на его результат и все их сложить, приходя к среднему или же ожидаемому результату. При умножении пусть даже большой вероятности, что Бога нет, на небольшую ценность приза получается величина возможно и большая, но всегда конечная. При умножении любой конечной, даже очень маленькой, вероятности, что Бог окажет человеку милость за его добродетельное поведение, на бесконечно большую ценность приза получается бесконечно большая величина. Паскаль осознавал: результат этих вычислений бесконечен, так что ожидаемый выигрыш от добродетельного поведения бесконечно положителен. Таким образом, Паскаль заключал: любой разумный человек будет следовать законам божьим. В наше время это утверждение известно как «пари Паскаля».

Несколько слов о лотереях. Администрация штата достаточно осведомлена о математическом ожидании. Сборы от продажи билетов всегда больше, чем сумма призовых. Однако в 1992 г. некоторые инвесторы в австралийском Мельбурне заметили, что в Вирджинской лотерее этот принцип нарушается. По условиям игры необходимо выбрать 6 чисел из группы от 1 до 44. Всего существует 7 059 052 способов. В математике это называется числом комбинаций:

Лотерейный джекпот составлял 27 млн. долларов, а если считать вместе со вторым, третьим и четвертым призами, то и все 28 млн. долларов. А по какой цене администрация штата Вирджиния, при всей ее мудрости, продает билеты? Как обычно: по 1 доллару. То есть, затраты на приобретение билетов составят всего 7 млн. долл.

Австралийцы быстро нашли 2500 мелких инвесторов в Австралии, Новой Зеландии, Европе и США, каждый из которых согласился вложить в среднем по 3 тыс. долларов. Однако план содержал в себе кое-какие риски. Во-первых, так как не они одни покупали билеты, существовала вероятность, что другой, и даже не один, а несколько окажутся с выигрышным билетом, то есть, выигрыш придется делить. Лотерея проводилась уже 170 раз; в 120 случаях победителя не оказывалось, в 40 случаях оказывался один победитель и лишь в 10 случаях – два. Если подобная частотность точно отражала ситуацию с шансами, тогда следовало, что в 120 случаях из 170 инвесторы получили бы весь выигрыш, в 40 случаях из 170 у них оказалась бы только половина, а в 10 случаях из 170 – лишь треть. Подсчитывая ожидаемый выигрыш с помощью принципа математического ожидания Паскаля, они пришли к следующей цифре: (120/170 х 27,9 млн. долларов) + (40/170 х 13,95 млн. долларов) + (10/170 x 6,975 млн. долларов) = 23,4 млн. долларов. Или 3,31 доллара за билет – неплохой доход с 1 доллара, даже после всех затрат.

Но существовала и другая опасность: кошмар системы логистики в связи с завершением выкупа всех билетов к окончанию срока розыгрыша. Могли потребоваться существенные незапланированные расходы, а значительную призовую сумму можно было так и не получить.

Члены инвестиционной группы тщательно подготовились. Они от руки, как того требуют правила, заполнили 1,4 млн. билетов: каждый билет участвовал в пяти розыгрышах. В 125 торговых точках расставили выкупщиков и заручились поддержкой продуктовых магазинов, которые получали доход с каждого проданного билета. Схема была запущена за трое суток до завершения лотереи. Служащие магазинов работали посменно, чтобы успеть продать как можно больше билетов. В одном магазине за последние двое суток продали 75 тыс. билетов. Другой магазин, сетевой, принял банковских чеков на 2,4 млн. билетов, распределил работу по печатанию билетов между своими торговыми точками и нанял курьеров, чтобы собрать их. И все-таки под конец группе не хватило времени: они купили всего 5 млн. билетов из 7 059 052.

Прошло несколько дней с момента объявления выигрышного билета, но за выигрышем никто не явился. Выиграл консорциум инвесторов, однако им пришлось ждать в течение нескольких дней, чтобы удостовериться в этом. Затем, когда чиновникам от государственной лотереи стало известно, что выиграл консорциум, они стали уклонялся от выплаты призовых денег. Последовал целый месяц пререканий между юристами той и другой сторон, пока чиновники не признали: у них нет причин для отказа в выплате. В конце концов, инвесторы свой выигрыш получили.

Глава 5. Противостояние законов больших и малых чисел

Чтобы работа из области теории случайности могла быть применена в реальном мире, необходимо задуматься над следующим вопросом: какова связь между неявными вероятностями и наблюдаемыми результатами? Когда мы говорим: шансы того, что кость упадет на 2, равны 1 из 6, что мы имеем в виду с практической точки зрения? Если это не значит, что при любой серии бросков кость упадет на 2 аккурат 1 раз из 6, то на чем тогда основывается наша уверенность, будто шансы бросить кость и получить 2 в самом деле равны 1 из 6? И что подразумевается, когда врач говорит: лекарство в 70% эффективно, в 1% случаев влечет за собой серьезные побочные эффекты? Или что при опросе выясняется: кандидата поддерживают 36% избирателей? Это непростые вопросы, они имеют отношение к самой сути понятия случайности, понятия, о котором математики до сих пор спорят.

Якоб Бернулли видел ответ на вопрос в следующем: вместо того, чтобы зависеть от данных нам вероятностей, мы должны определить их сами, посредством наблюдений. Допустим, перед вами вращаются несколько рулеточных колес. Как точно сможете вы определить неявные вероятности, и с какой долей уверенности? На этот вопрос Бернулли не смог ответить. Вместо этого он нашел ответ на вопрос, тесно связанный с вышеупомянутым: насколько четко неявные вероятности отражаются в реальных результатах? Бернулли принял за очевидное то, что мы вполне оправданно ожидаем: с увеличением числа попыток наблюдаемые периодичности с большей или меньшей точностью отразят неявные вероятности. Бернулли конечно же не был первым, кто так считал. Однако он стал первым, кто формально рассмотрел данную проблему, перевел идею в плоскость доказательства и выразил в количественной форме, задавая вопрос: сколько попыток необходимо и насколько уверенными мы можем быть?

Важнейшим достижением за все двадцать лет непрерывной работы Якоб Бернулли считал «золотую теорему». Ее современные версии известны под названиями: теорема Бернулли или закон больших чисел. Бернулли представил сосуд с 3 тыс. белых голышей и 2 тыс. черных, то есть в процентном соотношении как 60% и 40% соответственно. Вы наугад несколько раз вынимаете голыши из сосуда, но «с заменой», то есть перед тем, как вынуть следующий голыш, заменяете уже вынутый, чтобы сохранять соотношение 3 к 2. Таким образом, заранее известно, каковы шансы вынуть белый голыш: 3 из 5 или 60%. В связи с этим экспериментом основной вопрос Бернулли звучит так: насколько строго количество белых голышей будет держаться в рамках 60% и с какой вероятностью? В наше время подобную последовательность испытаний называют испытаниями по схеме Бернулли, а серию испытаний – процессом Бернулли.

Предположим, 60% избирателей в Базеле поддерживают мэра. Скольких человек необходимо опросить, чтобы шансы обнаружить, что мэра поддерживают от 58% до 62%, равнялись 99,9%? 25,5 тыс. человек… во времена Бернулли почти все население Базеля. Одна из причин того, почему численная оценка Бернулли была так далека от оптимальной, заключается в том, что в качестве стандарта достоверности он выбрал 99,9% – то есть, он предполагал, что получит неверный ответ (ответ, который отличается от верного более чем на 2%) менее чем в 1 случае из 1000. А это чересчур высокий стандарт. Бернулли назвал его моральной достоверностью, имея в виду степень достоверности, которой, по его мнению, должен обладать человек здравомыслящий, чтобы принять рациональное решение. В наше время мы отказались от понятия моральной достоверности в пользу того статистической значимости – подразумевая, что ваш ответ будет неверным менее чем в 1 случае из 20. Пользуясь современными математическими методами, статистики продемонстрировали, что в опросе, подобном описанному выше, можно получить статистически значимые результаты с точностью ±5%, опросив при этом всего 370 человек.

Если Бернулли требовался чрезмерно высокий стандарт достоверности, в реальных жизненных ситуациях мы часто совершаем ошибку прямо противоположную: предполагаем, что выборка или серия испытаний является репрезентативной, когда на самом деле она слишком малочисленна, чтобы быть надежной. Например, если во времена Бернулли вы опросили бы 5 жителей Базеля, подсчеты продемонстрировали бы: шансы того, что вы получите результат 60% (3 человека) поддержки мэра, равны всего 1 из 3. Так что если вы отнеслись к выборке из 5 человек серьезно, вы наверняка либо сильно переоценили, либо сильно недооценили истинную популярность мэра у населения.

Превратное представление – или ошибочное интуитивное чутье – относительно того, что небольшая выборка точно отразит неявные вероятности, настолько распространено, что Канеман и Тверский дали ему название: закон малых чисел. На самом деле закон малых чисел – вовсе не закон. Это ироничное название, описывающее ошибочную попытку применить закон больших чисел в том случае, когда на самом деле числа не являются большими.

Вспомните о генеральных директорах 500 крупнейших мировых компаний, вошедших в рейтинг журнала «Форчун». Предположим, что для этих генеральных директоров удачные годы случаются с такой же периодичностью, что и в примерах с белыми голышами и сторонниками мэра: 60%. Шансы, что в течение заданного пятилетнего периода деятельность конкретного генерального директора отразит это, равны всего 1 к 3! В приложении к 500 компаниям это означало бы, что за последние пять лет около 333 генеральных директоров продемонстрировали уровень деятельности, не отражавший их реальные способности. Более того, следует ожидать, что совершенно случайно примерно 1 из 10 генеральных директоров продемонстрирует успех или же неудачу все пять лет подряд. Как выразился Бернулли, «не стоит оценивать людские деяния исходя из результатов».

Чтобы возражать против закона малых чисел, нужно обладать твердым характером. Потому как каждый может откинуться на спинку кресла и тыкать в итоговую строку отчета в качестве доказательства. Реальная же оценка знаний человека и его истинных навыков требует доверия, размышлений, верных суждений и, собственно, мужества.

Еще одно ошибочное понятие, связанное с законом больших чисел, состоит в следующем: событие произойдет с большей или меньшей вероятностью по той причине, что за последнее время оно происходило или не происходило. Представление о том, что шансы на событие с постоянной вероятностью возрастают или снижаются в зависимости от того, имело ли событие место в недавнем прошлом, называется заблуждением игрока.

Закон Бенфорда или закон первой цифры гласит, что в таблицах чисел, основанных на данных источников из реальной жизни, цифра 1 на первом месте встречается гораздо чаще, чем все остальные. Более того, чем больше цифра, тем меньше вероятность, что она будет стоять в числе на первом месте. Число 1 встречается в качестве первой цифры в 30% случаев; число 2 – примерно в 18% и так далее, до цифры 9, которая в качестве первой встречается лишь в 5% случаев. На этом свойстве может быть основана проверка естественности большого массива чисел (например, в бухгалтерских бумагах), подобно тому, как закон Ципфа проверяет естественность текстов (что уже используется поисковыми роботами в Интернет).

Глава 6. Ложная положительность и положительная ложность

Томас Байес родился в Лондоне в 1701 г., и был священником, имевшим приход в Танбридж-Уэлс. Байес умер в 1761 г. Неосведомленность об идеях Томаса Байеса лежит в основе многих серьезных ошибок, будто то медицинские диагнозы или судебные решения. Например, и вероятность того, что случайно выбранный человек окажется психически больным, и вероятность того, что случайно выбранный человек утверждает, будто жена читает его мысли, весьма низки, однако вероятность того, что человек психически болен, если он утверждает, будто жена читает его мысли, уже гораздо выше, как и вероятность того, что человек утверждает, будто жена читает его мысли, если при этом он психически болен. Как все эти вероятности связаны между собой? Ответ следует искать в области условных вероятностей.

На вероятность влияет тот факт, что событие произойдет, если или при условии, что произойдут другие события. В этом и заключается теория Байеса. Теорема Бернулли решает следующий вопрос: сколько получится орлов, если планируется произвести много бросков идеальной монеты, в то время как Байес исследовал первоначальную цель Бернулли – вопрос о том, насколько можно быть уверенным в том, что монета идеальна, если выпадает определенное число орлов. Байес разработал условную вероятность в попытке ответить на тот же вопрос, который увлек Бернулли: как по известному факту события вычислить вероятность того, что оно было вызвано данной причиной? Если в процессе клинических испытаний лекарство помогло 600 000 пациентов из 1 млн., шансы того, что оно подействует, приближаются к 60%. Однако к какому выводу вы придете, если будете исходить из испытаний меньшего масштаба? Байес задался и другим вопросом: если перед испытаниями у вас были основания верить в то, что лекарство эффективно лишь на 50%, насколько весомыми окажутся новые сведения для ваших дальнейших оценок? Наш жизненный опыт в основном выглядит следующим образом: мы наблюдаем сравнительно небольшую выборку исходов, а уже из этого выводим информацию и приходим к заключению относительно качеств, которые привели к подобным исходам. Как нам следует выводить информацию?

Байес задумал решить задачу через метафору. Предположим, нам выдали квадратный стол и два мяча. Первый мяч мы катим по столу таким образом, чтобы имели место равные вероятности: мяч остановится в любой точке. Наша цель – определить, не глядя, где именно вдоль всей оси слева направо мяч остановился. При этом наше орудие – второй мяч, который мы поначалу тоже будем неоднократно катать по столу тем же самым образом, что и первый. Байес продемонстрировал, как, опираясь па сведения о втором мяче, определять точную вероятность того, что первый мяч находится в любой данной точке рядом с осью слева направо. И продемонстрировал, как при наличии дополнительных сведении можно пересмотреть первоначальные подсчеты. Согласно терминологии Байеса, первоначальные подсчеты называются априорной вероятностью, а новые предположения – апостериорной вероятностью.

Ранее я рассмотрел пример: если в семье двое детей, какова вероятность двух девочек? Ответ ¼. Пространство элементарных событий: мальчик – мальчик, девочка – мальчик, мальчик – девочка, девочка – девочка. Далее я изменил условия: если в семье двое детей, и один из них – девочка; какова вероятность, что и второй ребенок тоже девочка. Урезаем пространство элементарных событий до трех вариантов: девочка – мальчик, мальчик – девочка, девочка – девочка. Все варианты представляются равновероятными, так что вероятность двух девочек в семье 1/3. Добавим еще одно условие. Допустим вам известно что один из детей – девочка по имени Флорида.

Обозначим девочку по имени Флорида как «девочка Ф.», а девочку по имени не Флорида как «девочка не Ф.». Первоначальное пространство элементарных событий было таким: (мальчик, мальчик), (мальчик, девочка Ф.), (мальчик, девочка не Ф.), (девочка Ф., мальчик), (девочка не Ф., мальчик), (девочка не Ф., девочка Ф.), (девочка Ф., девочка не Ф.), (девочка не Ф., девочка не Ф.), (девочка Ф., девочка Ф.).

Так как нам известно, что один из детей – девочка по имени Флорида, можно сократить пространство элементарных событий: (мальчик, девочка Ф.), (девочка Ф., мальчик), (девочка не Ф., девочка Ф.), (девочка Ф., девочка Ф.). Теперь видно, чем еще эта задача отличается от задачи про двух дочерей. Поскольку утверждения, что девочку зовут Флорида и девочку зовут не Флорида, нельзя назвать равновероятными, не являются таковыми и все элементы пространства элементарных событий.

В 1935, последнем году, за который Управление социальным обеспечением предоставило статистику в отношении имени, около 1 из 30 000 девочек были наречены именем Флорида. Поскольку имя становилось все менее популярным, предположим, что сегодня вероятность появления девочки по имени Флорида равна 1 из 1 млн. Это значит следующее: если нам станет известно, что определенную из двух девочку зовут не Флорида, ничего страшного, однако если мы узнаем, что ее зовут Флорида, можно сказать, что мы попали в точку. Вероятность того, что обеих девочек назовут именем Флорида (даже если мы проигнорируем тот факт, что обычно родители избегают давать детям одинаковые имена), настолько мала, что можно спокойно ею пренебречь. Итак, вот что у нас остается: (мальчик, девочка Ф.), (девочка Ф., мальчик), (девочка не Ф., девочка Ф.), (девочка Ф., девочка не Ф.). Все эти события в весьма хорошем приближении равновозможны.

Поскольку 2 из 4, то есть половина элементов пространства элементарных событий являются семьями с двумя девочками, ответом не может быть 1 из 3 – как это было в задаче с двумя дочерьми, – ответом является 1 из 2. Все дело в дополнительной информации – осведомленности насчет имени девочки.

Если вы по-прежнему сбиты с толку, то можно представить себе следующее: в очень-очень большой комнате мы собираем 75 млн. семей с двумя детьми, из которых хотя бы один ребенок – девочка. Как нам стало известно из задачи с двумя дочерьми, в комнате окажется около 25 млн. семей с двумя девочками и 50 млн. семей с одной девочкой (25 млн. семей, в которых девочка является старшим ребенком, и столько же семей, в которых девочка является младшим ребенком). Далее «урезаем»: просим остаться в комнате только те семьи, в которых есть девочки по имени Флорида. Поскольку Флорида – 1 имя на 1 млн. имен, останутся около 50 из 50 млн. семей с одной девочкой. А из 25 млн. семей с двумя девочками тоже останутся 50: 25 потому, что их первый ребенок назван по имени Флорида, другие 25 потому, что их младшая дочь названа Флоридой. В этом примере всех девочек можно представить как лотерейные билеты; в таком случае девочки по имени Флорида станут выигрышными билетами. И хотя семей, в которых один из двух детей – девочка, в два раза больше, чем семей, в которых оба ребенка – девочки, семьи с двумя девочками обладают двумя лотерейными билетами, поэтому среди выигравших будет примерно одинаковое соотношение семей с одной девочкой и семей с двумя девочками. [2]

Лично я наиболее яркими воспоминаниями, связанными с преподобным Байесом, обязан одной из пятниц 1989 г.: в тот день позвонил лечащий врачи и сообщил, что я инфицирован ВИЧ, причем достоверность этого прогноза составляет 999 из 1000. К счастью, врач перепутал вероятность того, что результаты моего анализа будут положительными, если я не являюсь ВИЧ-инфицированным, с вероятностью того, что я могу и не быть ВИЧ-инфицированным, даже если результаты моего анализа окажутся положительными. Чтобы разобраться, где ошибся врач, прибегнем к методу Байеса.

Возьмем пространство элементарных событий, и распределим членов этого пространства по категориям: тех, кто у кого анализы оказались ВИЧ-положительными и кто ВИЧ-положителен (истинная положительность), тех, у кого анализы оказались положительными, но кто на самом деле не положителен (ложная положительность); тех, у кого анализы оказались ВИЧ-отрицательными и кто ВИЧ-отрицателен (истинная отрицательность), тех, у кого анализы оказались ВИЧ-отрицательными, но кто на самом деле ВИЧ-положителен (ложная отрицательность). Сколько людей в каждой из этих категорий? Предположим, мы рассматриваем изначально население из 10 000 человек. Пользуясь статистическими данными узнаём, что в 1989 г. около 1 из 10 000 гетеросексуальных, не принимающих наркотиков белых американцев мужского пола, сдавших анализы, оказались ВИЧ-инфицированными. Предположим, что в категории «ложная отрицательность» показатель равен 0, тогда около 1 человека из каждых 10 000 сдавших анализы окажется положительным из-за наличия инфекции. К тому же поскольку показатель «ложной отрицательности» равен, по словам врача, 1 из 1000, наберется около 10 тех, кто не заражен ВИЧ, однако анализы которых тем не менее окажутся положительными. У остальных 9989 человек из 10 000, составляющих пространство элементарных событий, результаты анализов окажутся отрицательными.

Теперь «урежем» пространство элементарных событий – включим в него только тех, результаты анализов которых оказались положительными. У нас останется 10 человек из категории «ложная положительность» и 1 человек из категории «истинная положительность». Другими словами, лишь 1 человек из 11, результаты анализов которых оказались положительными, действительно ВИЧ-инфицирован. Врач сказал мне: вероятность того, что в анализе ошибка – на самом же деле я был совершенно здоров, – равна 1 из 1000. А на самом деле ему следовало сказать следующим образом: «Не волнуйтесь, шансы на то, что вы на самом Деле не инфицированы, выше 10 из 11».

Теория Байеса говорит о следующем: вероятность того, что А произойдет, если произойдет В, обычно отличается от вероятности того, что В произойдет, если произойдет А.

Если Форд знает, что у 1 из 100 его машин неисправна трансмиссия, при помощи «золотой теоремы» Можно узнать вероятность того, что в партии из 1000 машин 10 или более трансмиссий будут неисправными однако если Форд обнаружит 10 неисправных трансмиссий в выборке из 1000 машин, данный факт не сообщит автомобильной компании вероятность того, что среднее арифметическое неисправных трансмиссий равно 1 из 100. В жизни наиболее частой из данных примеров оказывается вторая постановка задачи: вне ситуации, связанной с азартными играми, мы обычно не обладаем теоретическими знаниями шансов, скорее нам приходится вычислять их, основываясь на серии наблюдений. Я специально выделил это различие – ввиду его важности. Оно определяет существенную разницу между вероятностью и статистикой: первая имеет дело с прогнозами на основе определенных вероятностей; последняя связана с заключениями на основе вероятностей, выведенных посредством серии наблюдений.

Глава 7. Измерение и закон распределения ошибок

Числам всегда приписывается особый вес. Рассуждение строится примерно так: если учитель оценивает сочинение но стобалльной шкале, эти незначительные различия и в самом деле что-то значат. Но если десять издателей сочли, что рукопись первого тома «Гарри Поттера» не заслуживает публикации, то каким образом бедная миссис Финнеган (учительница моего сына) проводит тонкое различение между двумя школьными сочинениями, ставя за одно 92 балла, а за другое 93? Если мы допускаем, что качество сочинения в принципе поддается определению, то нам придется признать, что оценка – не описание качества сочинения, но его измерение, а измерение, как ничто другое, подвержено случайности. В случае с сочинением измерительный инструмент – учитель, а в выставляемых им оценках, как и в любом измерении, проявляются случайная дисперсия и ошибки.

Вопрос неточности измерений приобрел особо важное значение в середине XVIII в. Ведущую роль здесь сыграл Пьер-Симон де Лаплас. Требования как астрономии, так и экспериментальной физики были таковы, что на долю математиков конца XVIII – начала XIX вв. выпали прежде всего осмысление и подсчет случайной ошибки. Их усилиями возникла новая область – математическая статистика, занимающаяся разработкой методов для интерпретации данных наблюдений и опытов. Один из парадоксов нашем жизни заключается в том, что хотя измерения всегда несут в себе некоторую погрешность, когда речь заходит об измерениях, реже всего говорят именно о погрешности.

Исследователи выяснили у 30 любителей колы, предпочитают ли они «Пепси-колу» или «Кока-колу», а потом попросили проверить свои предпочтения, продегустировав оба напитка, стоящие бок о бок, 21 человек из 30 сообщили, что проверка подтвердила их выбор, хотя коварные исследователи налили «Кока-колу» в бутылки от «Пепси-колы», и наоборот. Когда мы оцениваем или измеряем, наш мозг полагается отнюдь не только на непосредственно воспринимаемое, но использует и другие источники информации – например, ожидания.

Перед теорией измерения встает два вопроса: как получить число на основе ряда отличающихся друг от друга измерений? имея в виду, что число измерений ограничено, как вычислить вероятность того, что оценка верна?

Среди троих ученых, благодаря которым на колоколообразную кривую обратили внимание, реже всех воздается по заслугам именно ее первооткрывателю. Абрахам де Муавр совершил свое открытие в 1733 г. Де Муавр пришел к искомой форме кривой, когда пытался аппроксимировать числа, заполняющие треугольник Паскаля. Гистограммы для 10-й, 100-й и 1000-й строк треугольника Паскаля приведены на рис. 3.

Рис. 3. Построение колоколообразной кривой на основе треугольника Паскаля. Столбцы отображают относительную величину чисел в 10-м, 100-м и 1000-м рядах треугольника Паскаля. Числа по оси абсцисс – элементы строки треугольника, к которым относятся столбики. По традиции нумерация начинается с 0, а не с 1 (вторая и третья гистограммы обрезаны так, что элементы, столбики для которых имеют пренебрежимо малую высоту, на рисунке не представлены

Сегодня колоколообразную кривую называют обычно нормальным распределением, а иногда – Гауссовой кривой. Нормальное распределение – не отдельная фиксированная кривая, но целое семейство кривых, определяемых двумя параметрами, задающими положение кривой и ее форму. Первый из них – расположение пика: на рис. 3 это – 5, 50 и 500 соответственно. Второй – степень разброса. Этот показатель, получивший свое современное наименование лишь в 1894 г., называется стандартным отклонением. Грубо говоря, это половина ширины кривой в той точке, где кривая достигает своей 60%-ной высоты. Если данные распределены нормально, около 68% результатов измерений попадают в пределы одного стандартного отклонения, около 95% – в пределы двух стандартных отклонений и 99,7% – в пределы трех стандартных отклонений.

Как правило, при проведении опросов предел погрешности выше 5% считается недопустимым, однако в повседневной жизни мы основываем свои суждения на значительно меньшем количестве наблюдений. Разве найдешь человека, который 100 лет играет в профессиональный баскетбол, вложил деньги в 100 многоквартирных жилых домов или основал 100 компаний, выпускающих шоколадное печенье? Так что, когда мы делаем выводы об успешности этих людей, мы берем за основу лишь незначительное число наблюдений. Сталкиваясь с успехом или с неудачей, мы имеем дело лишь с одним наблюдением, с одной из множества точек колоколообразной кривой, отображающей все наблюдавшиеся ранее возможности. И мы не знаем, что представляет собой это наблюдение – среднее или явный выброс, событие, в котором можно быть абсолютно уверенным, или редкий случай, который едва ли повторится.

Тог факт, что нормальное распределение описывает распределение ошибки измерения, открыл десятилетия спустя после выхода работы де Муавра человек, имя которого носит колоколообразная кривая, – немецкий математик Карл Фридрих Гаусс.

Лаплас наткнулся на работу Гаусса в 1810 г. Читая работу Гаусса, Лаплас сразу же понял, что может использовать его открытие в целях совершенствования собственной работы, а его собственная работа, в свою очередь, намного убедительнее, чем это удалось Гауссу, доказывает: нормальное распределение является отражением закона распределения ошибок.

Глава 8. Упорядоченный хаос

Когда в XIX в. ученые начали разбираться в ставшей доступной социологической информации, куда бы они ни посмотрели, всюду им виделась одна и та же картина: хаос жизни превращался в измеримые и предсказуемые структуры. Но поразили ученых вовсе не одни лишь закономерности. Их поразила природа варьирования. Они обнаружили, что очень часто социологические данные подчиняются принципу нормального распределения. История статистического анализа информации, связанной с жизнью человека, началась еще в XI в., когда Вильгельм I Завоеватель учредил то, что по сути явилось первым бюро переписи населения. Править он начал в 1035 г.

В XVI в. мэр Лондона распорядился еженедельно составлять бюллетени смертности с целью учета крещеных и погребенных по приходам. Десятилетиями эти бюллетени составлялись нерегулярно, но в 1603 г., когда чума особенно свирепствовала, городское управление распорядилось вести учет еженедельно. Лавочнику по имени Джон Граунт учетные данные рассказали о многом. Из бюллетеня продолжительности жизни можно узнать о том, сколько человек из ста предположительно доживут до того или иного возраста (рис 4). К данным Граунта (колонка под названием «Лондон, 1662») я добавил колонки, показывающие те же данные для некоторых стран уже в наши дни. В 1662 г. Граунт опубликовал результаты своей аналитической работы, издав книгу «Наблюдения естественного и политического характера, основанные на бюллетенях смертности».

Рис. 4. Дополненная таблица бюллетеня продолжительности жизни Граунта

Идеи Лапласа развил Адольф Кетле, родившийся в Генте, Фландрия, 22 февраля 1796 г. Кетле наткнулся на полезное открытие: характер распределения случайностей настолько надежен, что в определенных социологических данных его искажение может быть воспринято как свидетельство правонарушения. Кетле не ставил перед собой цели найти применение своим идеям в судебных расследованиях. Он метил выше: разобраться с помощью принципа нормального распределения в природе людей и общества. Он утверждал: если разнообразие физических признаков у людей подчиняется все тому же закону, напрашивается вывод: мы представляем собой несовершенные копии прообраза. Кетле назвал этот прообраз l‘homme moyen, то есть «средний человек».

Тем не менее в математических изысканиях Кетле оказалось больше смысла, нежели в изысканиях социальной физики. Во-первых, не все то, что происходит в обществе, особенно в мире финансов, соответствует нормальному распределению. Например, если бы доходы от показа фильма распределялись нормально, большинство фильмов приносили бы некий средний доход, а две трети доходов от всех фильмов оставались бы в пределах среднего отклонения. Однако в кинематографическом бизнесе 20% фильмов приносят 80% доходов. Такие сферы деятельности, которые развиваются за счет хитов, хотя и совершенно непредсказуемы, повинуются совсем иному распределению, такому, для которого понятия «среднее» и «среднее отклонение» ничего не значат ввиду отсутствия «типичного» производства, а мега-хитовые выбросы, которые в обычной сфере деятельности бывают раз в несколько сот лет, тут происходят неизмеримо чаще. (Очень подробно о том, что экономические параметры не подчиняются нормальному распределению пишет Нассим Талеб в Черном лебеде. Прим. Багузина.)

Статистический анализ в биологии применил двоюродный брат Чарльза Дарвина Фрэнсис Гальтон. Он измерял характерные особенности отпечатков пальцев – потом, в 1901 г., эту практику распознавания по отпечаткам пальцев взяли на вооружение в Скотленд-Ярде. Он высчитал продолжительность жизни правителей и священников, которая оказалась такой же, как и у людей другого положения и рода деятельности, из чего Гальтон заключил: молитва в этом отношении не дает никаких преимуществ. Он верил, что и характер человека задается наследственностью и, как и физические черты, подчиняется принципу нормального распределения. Основываясь на этих идеях, Гальтон основал новую науку и назвал ее евгеникой: от греческих eu (хороший) и genos (рождение). Какими бы ни были плюсы и минусы евгеники, исследования Гальтона в области наследственности привели к открытию двух математических понятий, которые являются центральными в современной статистике. Первое открытие Гальтон совершил в 1875 г. обнаружив феномен, когда группа крайних результатов сопровождается результатами, которые в среднем менее экстремальны. Гальтон назвал это явление регрессией к среднему.

Вторым важным открытием и вкладом в статистику стало определение математического показателя, названного Гальтоном коэффициентом корреляции. Коэффициент корреляции – это число между –1 и 1; если оно приближается к ±1, две переменные связаны между собой линейно; ноль же означает отсутствие связи.

Исследования в области статистики продолжил Карл Пирсон, ученик Гальтона. Когда мы имеем дело с ограниченным количеством данных, кривая нормального распределения совершенной формы никогда не получится. В период становления статистики ученые, чтобы определить, действительно ли данные распределяются в соответствии с принципом нормального распределения, поступали очень просто: строили график и смотрели, какой получается кривая. Однако каким образом можно выразить количественно точность соответствия? Пирсон изобрел метод, называемый проверкой по критерию хи-квадрат, с помощью которого можно определить верность своего предположения относительно действительного соответствия набора данных нормальному распределению.

Через Гальтона работа Кетле проникла в биологию. Однако внесла она оживление и в физику: Джеймс Максвелл и Людвиг Больцман, двое из основателей статистической физики, черпали свое вдохновение из теорий Кетле (как и Дарвин с Достоевским, о теориях они прочитали в книге Бокля). Внес свой вклад в эту область науки и Альберт Эйнштейн, опубликовав в 1905 г. свою первую работу по относительности. И хотя этот труд Эйнштейна мало известен массам, в статистической физике он произвел революцию. И в научной литературе на эту работу Эйнштейна потом ссылались чаще, чем на любую другую его работу.

Работа Эйнштейна 1905 г. по статистической физике имела своей целью объяснение феномена, называемого броуновским движением. Феномен получил свое название по имени Роберта Броуна, ботаника, специалиста мирового класса по микроскопии и человека, который, как считается, первым внятно описал клеточное ядро. Броун неуклонно преследовал цель: с помощью наблюдений открыть источник жизненной силы, этот загадочный фактор, благодаря которому, как считалось в то время, объект наделялся свойствами живого существа. Искания Броуна были обречены на неудачу, но его заслугой является открытие и описание беспорядочного движения микроскопических частиц в жидкости. Броун не смог вскрыть причину этого явления. А вот Эйнштейну удалось с невероятной подробностью объяснить точный механизм броуновского движения. Случайное блуждание стало одним из основополагающих, а вскоре и одним из самых изучаемых процессов в природе.

Глава 9. Иллюзия закономерности и закономерность иллюзий

Люди избирают кратчайший путь и прибегают к помощи воображения, чтобы заполнить пробелы в данных невизуального характера. Как и в случае с визуальной информацией, на основании неточных и неполных сведений мы делаем выводы и приходим к заключению, что наша «картинка» отчетлива и достоверна. Но так ли это на самом деле? Разработав методы статистического анализа, ученые смогли оградить себя от ложных закономерностей и решить, поддерживает ли ряд наблюдений гипотезу или, напротив, мнимое подтверждение случайно. Один из этих методов – оценка статистической значимости – был разработан в 20-е гг. XX в. Р.А.Фишером, одним из величайших статистиков.

В какой момент мы примем гипотезу либо откажемся от нее? Это и выясняется с помощью оценки статистической значимости: формальной процедуры, позволяющей оценить вероятность того, что наши наблюдения соответствуют действительности, если данная гипотеза верна. Если вероятность невелика, мы отклоняем гипотезу. Если высока, мы ее принимаем. Тем не менее, даже если данные значимы на, скажем, 3%, тестируя 100 человек, не являющихся экстрасенсами, на наличие сверхъестественных способностей, вы должны быть готовы к тому, что несколько человек проявят экстрасенсорные способности.

В то время как в главе 8 рассматривалось, с какой поразительной регулярностью происходят случайные события, теперь мы подойдем к вопросу с другой стороны: проанализируем, каким образом события, на первый взгляд имеющие явную причину, могут на самом деле оказаться результатом случайности.

Канеман и Тверский проанализировали множество методов быстрой оценки характера данных и принятия решения в условиях неопределенности. Они назвали такие методы «сокращенными эвристическими [3] процедурами». Эвристические процедуры могут иногда приводить к систематическим ошибкам, которые Канеман и Тверский назвали «ошибками предвзятости».

Представьте некую последовательность событий. Это могут быть квартальные дивиденды или ряд удачных или неудачных свиданий, организованных сайтом знакомств. В обоих случаях, чем длиннее последовательность, тем выше вероятность, что обнаружится любая закономерность, какую только можно себе вообразить, причем исключительно случайно. Прекрасный пример привел математик Джордж Спенсер-Браун: в случайной последовательности 10 в степени 1 000 007 нулей и единиц следует ожидать, по меньшей мере, 10 отдельных последовательностей из 1 млн. нулей, расположенных подряд! Идея Спенсера-Брауна заключалась в том, что существует разница между случайным процессом и результатом такого процесса, который кажется случайным.

Компания «Аррlе» столкнулась с подобной проблемой в связи с методом случайной тасовки, который она изначально применяла в своих плеерах «iPod»: истинная случайность приводила к повторам, поэтому; когда пользователи слышали подряд одну и ту же песню или песни одного и того же певца, они считали, что тасовка дала сбой. Тогда компания сделала эту функцию «менее случайной, чтобы она воспринималась как более случайная».

Много усилий затрачивается на изучение моделей случайного успеха на финансовых рынках. Только по воле случая некоторые аналитики и паевые инвестиционные фонды непрестанно демонстрируют впечатляющий успех. И хотя многочисленные исследования доказывают, что былые удачи на рынке не гарантируют хорошие результаты в будущем – так как в большинстве своем они случайны, – все же многие согласны платить за рекомендации брокеров или опыт управляющих паевыми фондами.

Интерес к иллюзии везучести возник приблизительно в 1985 г., после публикации исследования Тверского и его коллег в журнале «Когнитивная психология». В статье «»Легкая рука» в баскетболе: ложное восприятие случайных последовательностей» группа Тверского привела результаты исследования баскетбольной статистики. Исследователи сформулировали вопрос: как количество и продолжительность серий попаданий и промахов можно сопоставить с тем, что бы мы наблюдали, если бы результат каждого броска определялся случайным процессом. Например, как бы все обернулось, если вместо того, чтобы бросать мяч, игроки бросали бы монету и таким образом оценивали вероятность попадания в корзину. Обнаружилось, что, несмотря на удачные и неудачные серии, результаты бросков с площадки не предоставили никаких доказательств неслучайного поведения.

Люди любят контролировать все и вся. Наша страсть контролировать события имеет под собой основания, поскольку чувство личного контроля неотделимо от представления о собственной личности и самооценки. Одной из первых психологию контроля стала изучать психолог и художник-любитель, профессор Гарвардского университета Эллен Лангер. Почему потребность человека в контроле рассматривается в связи со случайными закономерностями? Дело в том, что если события случайны, мы не контролируем их, и если мы контролируем события, то они не случайны. Таким образом, сталкиваются наша потребность в контроле и паша способность распознавать случайность. Эта коллизия – одна из основных причин, по которой мы неверно истолковываем случайные события. Как накисала Лангер, «хотя люди могут лицемерно превозносить власть шанса, они ведут себя так, будто случайные события находятся в их власти».

Исследование показало: иллюзия контроля над случайными событиями усиливается, когда дело касается финансов, спорта и особенно бизнеса. Когда мы находимся во власти иллюзии или когда у нас есть новая идея (что одно и то же), мы обычно пытаемся найти примеры, подтверждающие, а не опровергающие ее. Психологи называют это «ошибкой подтверждения», и она очень мешает освободиться от неверной интерпретации случайных явлений. Как в 1620 г. написал философ Френсис Бэкон, «человеческий разум, однажды восприняв некое убеждение, собирает любые примеры, которые его подтверждают, и, несмотря на то, что противоположные примеры могут быть более многочисленными и весомыми, он либо не замечает, либо отвергает их, чтобы оставаться непоколебимым в своем убеждении».

Усугубляя положение, мы не только отдаем предпочтение фактам, подтверждающим наше предвзятое мнение, но еще и интерпретируем в пользу своих идей явления неоднозначные. Например, если мы прониклись доверием к какому-нибудь политическому деятелю, то хорошие результаты мы трактуем как его достижения, а в неудачах виним обстоятельства или соперников.

Даже случайные закономерности можно интерпретировать как убедительные доказательства, если они поддерживают предвзятое мнение. В повседневных ситуациях ошибка подтверждения нередко приводит к печальным последствиям. Когда преподаватель изначально считает, что один из учеников умнее других, он избирательно фокусируется на фактах, которые поддерживают его гипотезу. Когда при приеме на работу проводят собеседование с перспективным сотрудником, обычно первое впечатление складывается у работодателя мгновенно, и в оставшуюся часть собеседования он ищет подтверждения своей правоте.

Человеческий мозг развил способность распознавать закономерности, но, как показывают примеры ошибки подтверждения, мы фокусируемся на выявлении и подтверждении закономерностей, а не на том, чтобы минимизировать неверные заключения. И все же не стоит впадать в уныние, так как переступить через собственные предрассудки возможно. Стоит лишь понять: случайные события также могут предстать в виде закономерности. Следующий важный шаг – научиться подвергать сомнению свои ощущения и предположения. Наконец, имеет смысл уделять достаточно времени поискам доказательств собственной неправоты, точно так же, как мы тратим время на то, чтобы отыскивать доказательства своей правоты.

Глава 10. Походкой пьяного

Лаплас придерживался теории, называемой детерминизмом. Он считал, что состояние, в котором пребывает вселенная в настоящий момент, однозначно определяет то, каким образом будет развиваться ее будущее (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей). Применительно к повседневной жизни детерминизм описывает устройство мира, при котором наши личные качества, проявленные в данной конкретной ситуации или окружении, прямо и недвусмысленно ведут к точно определенным последствиям. Иными словами, мир является упорядоченным, в нем все можно предвидеть, просчитать, предсказать.

Начиная с позднего Возрождения и заканчивая Викторианской эпохой, многие ученые, изучавшие дела человеческие, придерживались детерминизма, подобно Лапласу. Некоторые разделяли точку зрения Гальтона, полагая, что наш жизненный путь однозначно определяется нашими личными качествами; Другие, вслед за Кетле, считали, что будущее общества можно предсказать. Зачастую такие ученые, вдохновленные успехами ньютоновской физики, высказывали теории о том, что человеческое поведение можно предсказать с той же долей достоверности, что и любое другое природное явление. Им казалось логичным, что предстоящие события должны быть определены настоящим положением дел, точно так же, как движение планет определяется их орбитами.

В 1960-х гг. американский метеоролог Эдвард Лоренц попытался задействовать новейшую для своих дней технологию (простейший компьютер), чтобы проверить на практике теорию Лапласа в одной отдельно взятой области – предсказании погоды. Лоренц проводил циклы расчетов, и во втором цикле использовал распечатку промежуточных результатов первого цикла. Он рассчитывал, что компьютер восполнит недостающие данные, взяв их из предыдущей модели, а потом произведет дальнейшие расчеты. Но что-то пошло не так: получившийся в результате прогноз погоды разительно отличался от предшествующего. Вместо того чтобы точно воспроизвести конечные расчеты из предыдущей модели, машина выдала совершенно новые данные. Вскоре ученый догадался, почему так произошло: в памяти компьютера данные хранились с точностью до шестого знака после запятой, а на печать они выводились с точностью лишь до третьего знака. В результате новые вводные данные несколько отличались от изначальных. В частности, число 0,293416 превратилось в 0,293. Ученые привыкли считать, что небольшое изменение исходных параметров ведет к небольшому изменению в развитии описываемой системы. Однако Лоренц обнаружил, что даже при таких малейших расхождениях результаты будут коренным образом отличаться. Это явление получило название «эффект бабочки». Эффект основан на допущении, что даже малейшие изменения в атмосфере, вызванные, скажем, взмахами крыльев бабочки, в будущем могут оказать колоссальное влияние на синоптическую ситуацию во всем мире.

Подводя итоги, можно сказать, что модель детерминизма не подходит для описания человеческой жизни. Или, как сказал лауреат Нобелевской премии Макс Борн: «Теория случайности более фундаментальна, чем теория обусловленности».

В нашем исследовании «походка пьяного» – некий архетип. Это настолько же подходящая модель для описания нашей с вами повседневной жизни, насколько частички пыльцы в жидкости подходят для описания броуновского движения: случайные события точно так же подталкивают нас сначала в одну, потом в другую сторону. И все, что касается наших личных достижений, работы, друзей, финансового положения, в гораздо большей степени зависит от случайности, чем думает большинство из нас. Дальше я постараюсь убедить вас, что во всем, за исключением разве что каких-то простейших поступков, на нас влияют непредвиденные обстоятельства и непредсказуемые силы. Свое построение я начну с явно противоположного утверждения: если будущее и в самом деле хаотично и непредсказуемо, почему, когда события уже произошли, нам часто кажется, что мы могли их предвидеть?

В любой сложной цепочке событий, где каждое отдельно взятое событие содержит некоторый элемент неопределенности, имеется принципиальная асимметрия между прошлым и будущим. Эта асимметрия привлекала внимание многих ученых, начиная с Больцмана, который занимался статистическим анализом молекулярных процессов, определяющих свойства жидкостей. Представьте себе, к примеру; молекулу красителя в стакане с водой. Молекула будет, подвержена броуновскому движению. Спустя три часа мы обнаружим, что молекула переместилась примерно на два с половиной сантиметра от того места, где началось ее движение. Вообразим, будто мы углубляемся в прошлое молекулы. Нам стали известны данные обо всех ее столкновениях с другими частицами. Мы узнаем, что при столкновении с первой молекулой воды наша молекула красителя начала свой зигзагообразный путь к той точке, где она пребывает сейчас. Иными словами, ретроспективно мы сможем точно объяснить, почему прошлое молекулы красителя развивалось именно таким образом. Но в стакане воды содержится множество других молекул воды, которые потенциально могли бы прийти во взаимодействие с нашей молекулой красителя. Чтобы заранее предсказать траекторию движения молекулы красителя, нам потребовалось бы рассчитать траекторию движения и взаимодействие всех этих потенциально важных в данном случае молекул воды. Для этого нам необходимо было бы выполнить невообразимое количество математических подсчетов, по объему и сложности во много раз превышающих расчеты столкновений частиц, которые нам пришлось бы выполнить, чтобы объяснить прошлое. Иными словами, траекторию движения молекулы красителя предсказать заранее практически невозможно, даже несмотря на то, что ретроспективно понять ее относительно легко.

Эта принципиальная асимметрия и объясняет тот факт, что некоторые события повседневной жизни, случившись, кажутся очевидными, хотя мы и не могли предвидеть их заранее. Именно поэтому синоптики могут объяснить причины, по которым три дня назад холодный атмосферный фронт сместился туда-то, а накануне теплый атмосферный фронт переместился в другое место. Но когда нужно предсказать, как будут вести себя атмосферные фронты через три дня те же самые синоптики гораздо менее точны в своих выкладках.

То же самое справедливо и для торгов на фондовой бирже. Возьмем, например, график показателей работы 800 управляющих паевых инвестиционных фондов за пять лет: с 1991 по 1995 гг. (рис. 5).

Рис. 5. Рейтинг управляющих паевыми инвестиционными фондами в период с 1991 по 1995 г.

По вертикальной оси мы отложили прибыли и убытки паевого инвестиционного фонда относительно среднего значения. Иными словами, отметка 0% означает, что доходность данного фонда соответствовала среднему значению в течение указанных пяти лет. По горизонтальной оси мы расположили показатели эффективности работы управляющих от первого до восьмисотого. Мало кто из инвесторов выберет фонд, который зарабатывал за предыдущие пять лет в среднем на 10% меньше, чем в среднем по группе, при условии, что есть фонд, доходность которого была на 10% выше средней. Глядя в прошлое, легко строить красивые графики и давать убедительные объяснения, но эта логически выверенная картина событий – всего лишь иллюзия, которую нам дает ретроспективный взгляд. Она имеет весьма опосредованное отношение к предсказанию будущего. Например, в графике на рис. 6, я сравниваю доходность тех же фондов за следующие пять лет, сохранив порядок их расположения, как в вышеприведенном графике. Иными словами, я сохраняю порядок расположения фондов по степени доходности за 1991-1995 гг., но накладываю на этот порядок их доходность за 1996-2000 гг.

Рис. 6. Порядок управляющих тот же, что и на рис. 5, а доходность указана за период 1996-2000 гг.

Мы без всяких на то оснований верим в то, что ошибки, допущенные в прошлом, являются следствием незнания или некомпетентности, и их можно было бы избежать, изучив вопрос тщательнее или проявив большую проницательность.

Историки, сделавшие изучение прошлого своей профессией, не менее настороженно, чем естествоиспытатели, относятся к мысли о том, что события развиваются предсказуемым образом. Вот что говорила по этому поводу историк Роберта Вольстеттер: «После того, как событие произошло, все сигналы, конечно же, становятся предельно ясными: теперь мы видим, какую беду они предвещали… Однако до того, как событие случилось, сигналы туманны и носят в себе множество противоречивых смыслов».

Чем дольше мы изучаем случайность, тем больше убеждаемся, что ясно видеть причины событий можно, к сожалению, после того, как события произошли.

Можно постараться выработать у себя иммунитет к ошибкам интуиции. Можно научиться относиться к ретроспективным объяснениям и предсказаниям с определенной долей скептицизма. Можно направить свои усилия на то, чтобы оперативно реагировать на события, а не полагаться на способность их предсказать, и здесь пригодятся такие качества, как гибкость, уверенность, смелость, упорство. А еще можно больше внимания обращать на то, какое впечатление человек производит сам по себе, а не на его достижения в прошлом. Такой подход поможет устоять против искушения выносить суждения, исходя из детерминистической системы взглядов, к которой мы, не задумываясь, прибегаем.

Профессор социологии из Йельского университета Чарльзу Перроу создал новую теорию несчастных случаев: в сложных системах (к которым я причисляю и человеческую жизнь) самые незначительные факторы, на которые обычно можно не обращать никакого внимания, иногда совершенно случайно влекут за собой масштабные последствия.

Перроу в своей теории отмечает, что современные системы включают в себя тысячи элементов, в том числе и ненадежный человеческий фактор, а взаимодействия этих элементов настолько сложны, что по отдельности эти взаимодействия невозможно проследить или предсказать. Так что катастрофы рано или поздно случаются. Эта теория получила название теории «нормальных несчастных случаев». Теория Перроу описывает, как несчастный случай может произойти без явных причин, вопиющих ошибок и людей, допустивших преступную халатность, которых ищут комиссии по расследованию, назначаемые компанией или государством. Помимо этого, теория нормальных несчастных случаев объясняет, почему иногда все неизбежным образом идет наперекосяк.

Неверно считать, что чем более выдающийся человек перед нами, тем он богаче. Нам не дано видеть возможности людей, мы судим только по достигнутому ими результату, и поэтому зачастую делаем о них ошибочные выводы, полагая, что достигнутые результаты в полной мере отражают личность человека. Теория нормальных несчастных случаев доказывает не то, что связь между поступком и наградой случайна, а то, что случайные события играют в нашей жизни ничуть не менее важную роль, чем наши личные качества и действия.

Мы потому не замечаем влияние случайностей на наши судьбы, что, приходя в этот мир, всеми силами стараемся видеть то, что мы хотим видеть. Иными словами, мы измеряем степень таланта степенью успеха, и уже потом выявляем это соответствие в подкрепление наших причинно-следственных выкладок. Именно поэтому нет особых различий между способностями человека, пользующегося бешеным успехом, и человека менее популярного. Разница между ними лишь в том, как эти способности воспринимаются.

Стать жертвой ожиданий легко, но не менее сложно и эксплуатировать их. Специалисты по маркетингу прекрасно знают об этой особенности человеческого восприятия и разрабатывают рекламные кампании так, чтобы эксплуатировать наши ожидания. Особенно эффективно это в таком сегменте рынка, как продажа водки. Водка – это нейтральный напиток, который дистиллируют, согласно принятым в США стандартам, «так, чтобы у нее не было различимого характерного запаха, вкуса или цвета». Однако, благодаря масштабным рекламным кампаниям, производители водки сумели создать у потребителей весьма сильные ожидания разницы. В итоге люди и правда верят, что этот напиток, который по определению не обладает характерными вкусовыми особенностями, на самом деле различается по вкусу в зависимости от производителя. Более того, потребители готовы платить за эти различия немалые деньги. Можно взять несколько сортов водки, пригласить несколько людей, разбирающихся в ней, и провести тест «вслепую». Наивысшую оценку получила дешевая водка марки «Smirnoff», которую продают во всех барах. Мы с вами оценивали бы мир совсем по-другому, если бы наши суждения были свободны от ожиданий и основывались только на существенных сведениях.

Томас Эдисон: «Многие из тех, кто потерпел в жизни неудачу, — это люди, не понимавшие, как близко они находились к успеху в тот момент, когда сдались».

Всех, кто старается чего-либо достичь, надо оценивать больше по их способностям, чем по достигнутым ими успехам. Легко делать героев из наиболее успешных личностей, а на остальных смотреть свысока. Но наличие способностей еще не гарантирует успеха, больше того, успех не находится в пропорциональной зависимости от способностей. Поэтому всегда надо держать в голове другую переменную нашего уравнения – роль случая.

Для меня главный вывод из этого в том, что ни в коем случае нельзя останавливаться на полдороге и поворачивать назад, ибо раз случайность играет определенную роль в нашей жизни, то один из важнейших факторов, определяющих успех, находится под нашим контролем, а именно – количество шагов, количество использованных шансов и возможностей. Потому как даже когда мы подбрасываем монету и она уже готова упасть невыигрышной для нас стороной, все же существует вероятность, что в самый последний момент монета перевернется, и мы выиграем. Или, как сказал Томас Уотсон, стоявший у истоков корпорации IВМ: «Если вы хотите преуспеть, удвойте частоту своих неудач».

Близкая по теме книга — Питер Бернстайн. Против богов. Укрощение риска.

[1] На русском языке вышла книга Канеман Д., Словик П., Тверски А. Принятие решений в неопределенности: Правила и предубеждения. Книга сразу же стал бестселлером, так что в бумажном виде ее не найти. О популярности книги говорит тот факт, что букинисты за нее хотят 3–5 тыс. руб.

[2] Здесь я могу заметить, что я не математик, и уже несколько раз читал о Байесовском подходе ранее. Но только сейчас благодаря объяснению Млодинова, я, как мне кажется, довольно неплохо разобрался в этой концепции… 🙂

[3] Эвристика (от др.-греч. ευρίσκω — «отыскиваю», «открываю») — отрасль знания, изучающая творческое, неосознанное мышление человека. Эвристика связана с психологией, физиологией высшей нервной деятельности, кибернетикой и другими науками, но сама как наука ещё полностью не сформировалась.

5 комментариев для “Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью”

Никита 27.12.2012 в 03:50

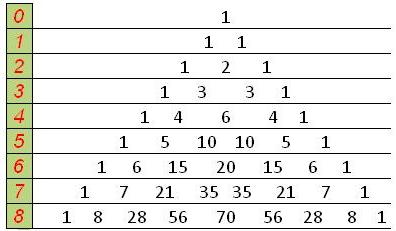
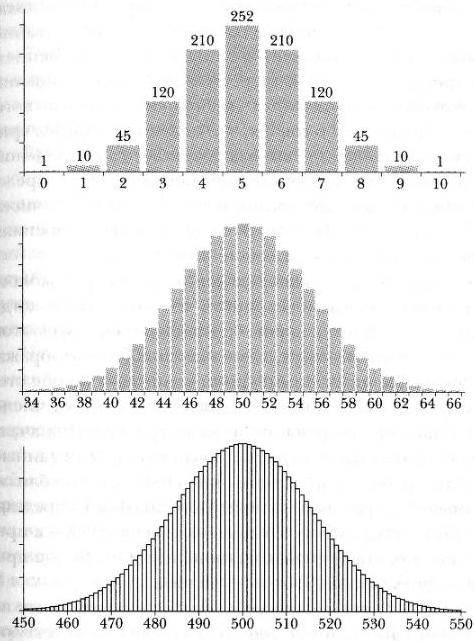
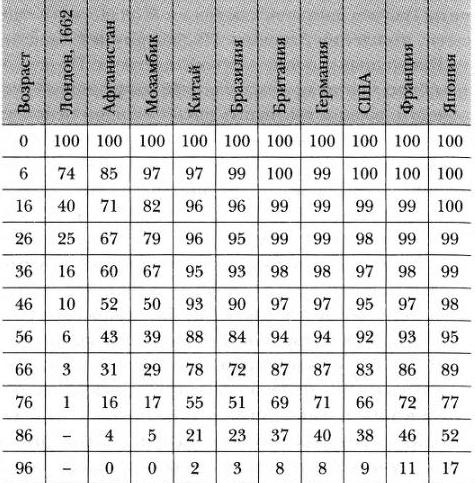
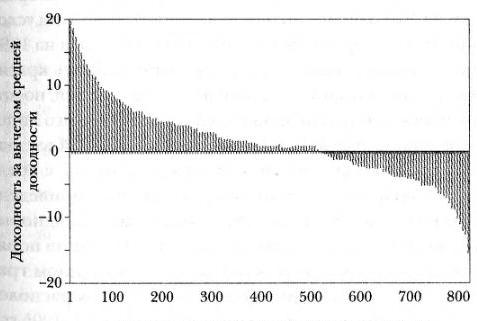
Супер-статья! Спасибо большое!

Немного пошевелил мозгами; вспомнил и дополнил то, чему учили в вузе; и получил новые знания.
Александр Куьмин 16.04.2013 в 03:42

Читал эту книгу, без преувеличения скажу что она вошла в тройку лучших книг за год. Я правда, не во всем согласился с автором, помимо случайности в спорте есть еще такое понятие как мастерство. У каждого игрока свой уровень.
Благодаря книге получил обширную пищу для ума.
uhbif19 31.10.2014 в 08:03

Восхитительный пост, большое спасибо!

Мне очень нравяться ваши пересказы книг: приятно написано и большая плотность информации.
Юоия 29.07.2021 в 21:01

А вот по поводу расхваливал пилотов и у них на следующей день получалось хуже.А когда кричал то лучше не охотно соглашаюсь я.Кричать орать это проще всего ,а вот когда пряником тут сложнее и по моему мнению всё таки лучше пряником.Ну может быть это действительно не для всех.Ну тогда какой это пилот если на него только кричать.)))
Юлия 29.07.2021 в 21:02

👌👍

Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью

5 комментариев для “Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью”

Добавить комментарий