Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. В этой серии ранее опубликовал Среднеквадратичное отклонение и среднее абсолютное отклонение, Моделирование сходимости центральной предельной теоремы. В настоящей заметке рассматривается мета-распределение p-значений, относящееся к распределениям с жирными хвостами.
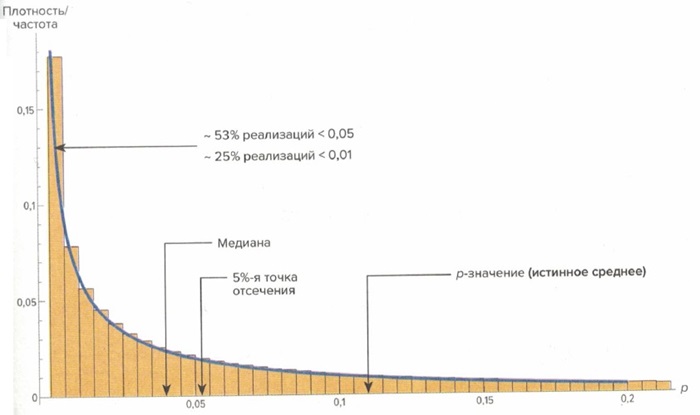
Рис. 1. Распределение вероятностей однохвостого p-значения при математическом ожидании 0,11, сгенерированное как методом Монте-Карло (гистограмма), так и аналитически (график непрерывной линией). Грубая асимметрия распределения делает среднее значение существенно выше большинства наблюдений, создавая многочисленные иллюзии статистической значимости.
Скачать заметку в формате Word или pdf
Манипуляции с р-значения в научной среде известны давно (см., например, Майкл Херцог. Статистика и планирование эксперимента для непосвященных). Подход Нассима Талеба меня заинтересовал своей новизной. Вместо того, чтобы анализировать р-значения, встречающиеся в различных работах, он моделирует распределение вероятностей p-значений (мета-распределение) для ансамблей статистически одинаковых явлений.
Он показывает, что p-значения асимметричны и волатильны, независимо от размера выборки n, и сильно варьируют при повторении с теми же протоколами в отношении идентичных копий того же стохастического процесса. Из-за этой волатильности минимальное p-значение, встречающееся в научных работах, существенно смещено от «истинного». С теоретико-вероятностной точки зрения ни р-значение 0,05, ни статистическая мощность 0,9 ничего не дают.
Если мы знаем «истинное» p-значение ps, как будут выглядеть его реализации в различных попытках на идентичных копиях одного и того же статистического явления? Под истинным значением ps мы подразумеваем ожидаемое значение согласно закону больших чисел на ансамбле m возможных выборок исследуемого явления:
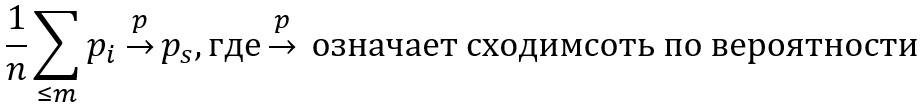
Аналогичный анализ сходимости можно предложить в отношении соответствующей «истинной медианы pM. Талебу не удалось получить явное выражение для ps, но он смог получить его для pM. В итоге он смог вывести формулу для распределения p-значений, позволяющую понять смещения в научных исследованиях.
Оказалось (см. рис. 1), что распределение крайне асимметрично, перекошено вправо, так что 75% реализаций «истинного» p-значения 0,05 будут оценены < 0,05 (и если по протоколу положено признавать успешное наблюдение некоторого явления на основании полученных данных, когда вероятность, что они всего лишь игра случая, ниже 0,05, то пограничные по надежности попытки пронаблюдать явление будут признаны втрое чаще, чем отвергнуты). Что еще хуже, 60% случаев с истинным р-значением 0,12 будут оценены ниже 0,05.
Распределение ведет себя как крайне жирнохвостое. Так, при наблюдаемом р-значении 0,02 «истинное» p-значение, скорее всего, >0,1 (и вполне может приблизиться к 0,2), притом что среднеквадратическое отклонение > 0,2 (то есть получился плюс-минус слон) и среднее отклонение около 0,35 (то есть получился слон плюс-минус два слона). Из-за суровой асимметрии оценка дисперсии сильно варьирует в зависимости от ps; таким образом, среднеквадратическое отклонение не является пропорциональным: когда по выборке р-значение 0,01, есть существенная вероятность, что истинное значение ps > 0,3.
Итак, рассуждая о р-значениях, мы не знаем, о чем говорим.
Можно смело утверждать, что при такой стохастичности реализаций р-значений и распределения их минимума желающие иметь пресловутую 5%-ную доверительность – и с опорой на нее делать статистические выводы – должны требовать p-значения на добрый порядок ниже.
Авторам, пытающимся исследовать воспроизводимость, следовало бы учесть предел погрешности в собственной процедуре и существенное смещение в сторону желаемых ими результатов (ошибка первого типа). Неудивительно, что тесты, исходно показавшие значимость, не достигают ее при воспроизведении; на самом деле удивительным было бы как раз воспроизведение результатов, исходно показавших значимость близкую к пограничной.
Статистическая мощность теста имеет ту же проблему, если не снизить p-значение или не переставить планку теста на более высокий уровень, такой как 0,99.