Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. В этой серии уже опубликовал Среднеквадратичное отклонение и среднее абсолютное отклонение. Настоящая заметка посвящена экспериментам со сходимостью центральной предельной теоремы (ЦПТ).
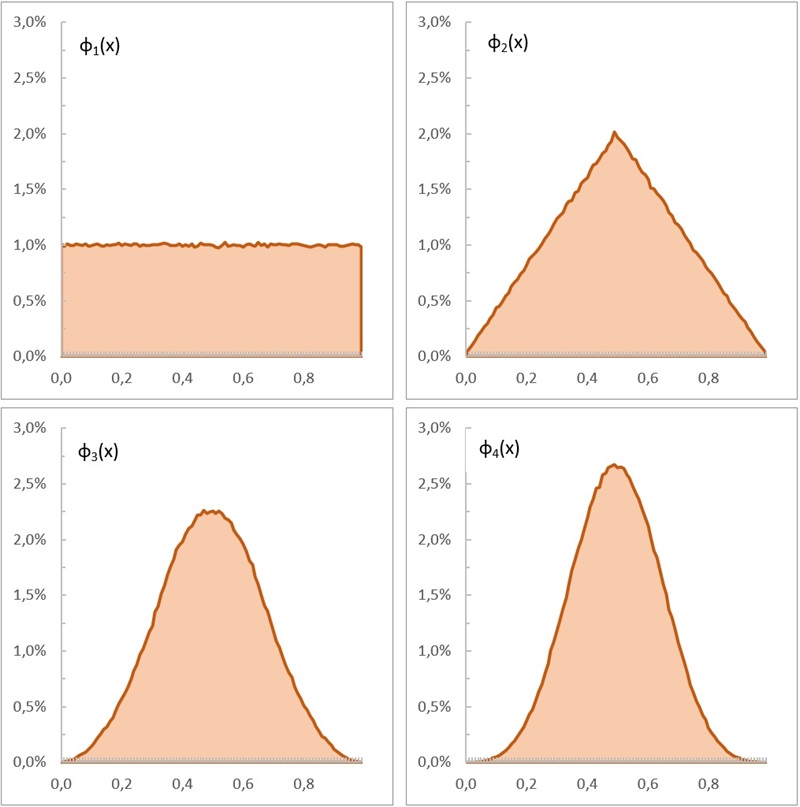
Рис. 1. Самая быстрая ЦПТ: равномерное распределение сходится к гауссову за несколько шагов
Скачать заметку в формате Word или pdf, примеры в формате zip (внутри Excel-файлы с моделированием случайных величин)
При конечной дисперсии случайных величин X устойчивое распределение суммы этих случайных величин Xs будет гауссовым. Однако случайная величина Xs построена как предельный переход при n –> ∞, и возможны разные осложнения на пути к цели. Рассмотрим несколько случаев, иллюстрирующих смысл ЦПТ и скорость сходимости.
Быстрая сходимость: равномерное распределение
Равномерное распределение – простейшее из всех. Если случайная величина X1 пробегает отрезок [0, 1], плотность вероятности φ1(х) будет постоянной при 0 ≤ х ≤ 1, давая интеграл 1. Теперь прибавим к ней другую случайную величину X2, независимую и с таким же распределением. У суммы X1 + X2 распределение будет другим! График плотности вероятности для суммы φ2(x) стал треугольным (см. рис. 1). Добавим еще одну переменную, и плотность вероятности φ3 для распределения суммы X1 + X2 + X3 станет колоколом. Нам потребовалось всего-навсего три слагаемых. Распределение суммы n равномерно распределенных независимых одинаково распределенных случайных величин называется распределением Ирвина – Холла.
В Excel я генерил случайную равномерно распределенную на отрезке [0,1] величину формулой =СЛМАССИВ(n;;0;1;ЛОЖЬ), где n – число итераций. Для генерации S2 = X1 + X2 я использовал среднее двух массивов =(СЛМАССИВ(n;;0;1;ЛОЖЬ)+СЛМАССИВ(n;;0;1;ЛОЖЬ))/2.
Полузамедленная сходимость: экспоненциальные распределения
Рассмотрим сумму случайных величин с экспоненциальным распределением. Исходная функция плотности вероятности
![]()
а для n слагаемых
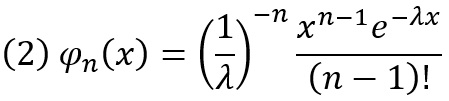
Это с точностью до обозначений соответствует гамма распределению Г(х|n,1/λ). В Excel для гамма распределения есть прямая и обратная функции ГАММА.РАСП() и ГАММА.ОБР(). Я сгенерил четыре выборки по 106 случайных чисел с помощью формулы
=ГАММА.ОБР(СЛМАССИВ(1 000 000;;0;1;ЛОЖЬ);n;1). Фрагмент СЛМАССИВ(1 000 000;;0;1;ЛОЖЬ) генерит миллион десятичных случайных чисел от 0 до 1 – вероятности р для внешней функции ГАММА.ОБР(р;n;1/λ). Для простоты я использовал λ = 1. n – число суммируемых экспоненциально распределенных случайных величин, n = 1, 3, 5, 10.
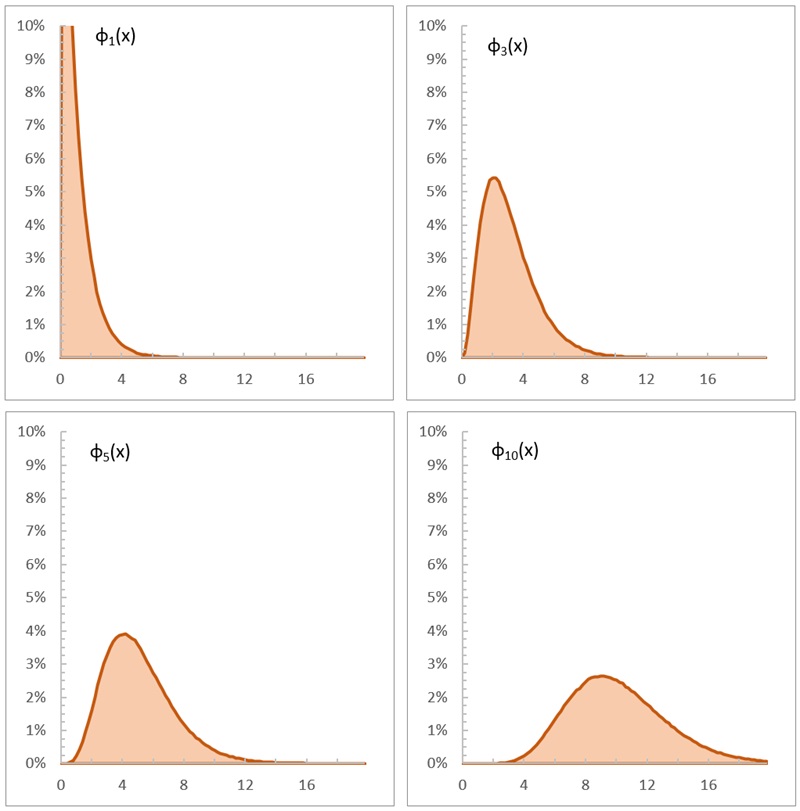
Рис. 2. Экспоненциальное распределение φ с числом слагаемых, указанном в нижнем индексе. Сходимость замедлилась по сравнению с равномерным распределением, но еще хорошая
Видно, что продвижение к гауссиане происходит медленнее, чем для равномерного распределения. Остатки изначальной асимметрии заметны даже при n = 10.
Медленный Парето
Плотность вероятности распределения Парето:
![]()
где x – значение случайной величины, α – показатель распределения, он же параметр формы, xmin – минимальное значение, которое может принимать случайная величина.
Стандартное распределение Парето определено на интервале [1,∞) для xmin = 1. Рассмотрим стандартное распределение Парето с α = 2:
![]()
Его обратное распределение
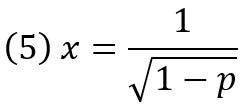
… позволяет генерировать в Excel случайную величину, соответствующую распределению (4) по формуле =1/КОРЕНЬ(1-СЛМАССИВ(n;;0;1;ЛОЖЬ)), здесь n – опять число итераций.
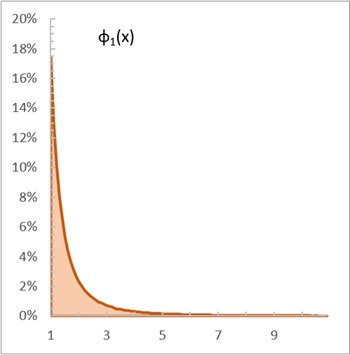
Рис. 3. Плотность вероятности стандартного распределения Парето с α = 2. График построен в Excel методом Монте-Карло на основе формулы (5). 106 итераций
Представить аналитически выражение для суммы независимых случайных величин, каждая из которых распределена по (4), пока не удалось. Талеб интегрировал численно.
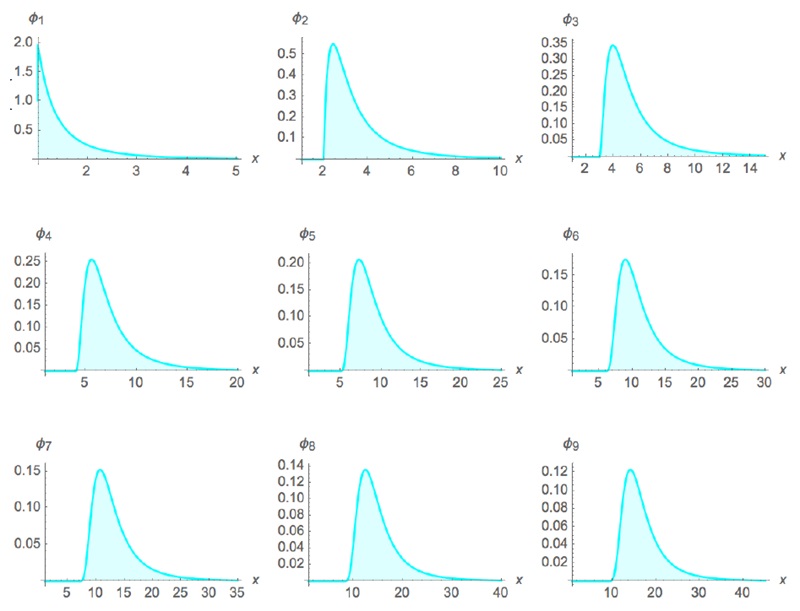
Рис. 4. Распределение Парето. Коэффициент асимметрии упорно не падает до нуля, хотя распределение сходится к Гауссовому… в конце концов
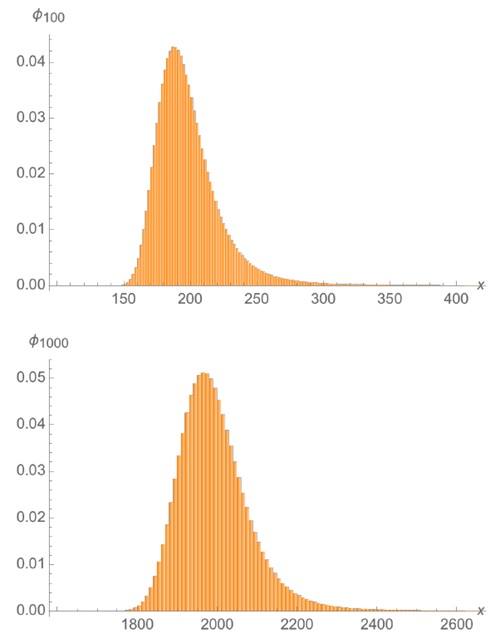
Рис. 5. Распределения Парето φ100 и φ1000 так и не приблизились к гауссиане, хотя при α = 2 это произойдет – если у вас хватит терпения и вы будете жить долго-долго
Полукубический Парето и его область сходимости
Интерес представляет случай α = 3/2. В определенном смысле слова оно еще более жирнохвостое. Чем меньше α, тем жирнее хвост.
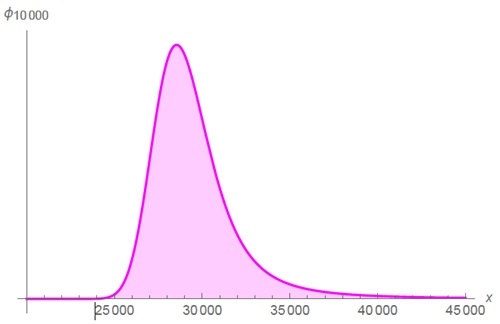
Рис. 6. Полукубическое распределение Парето так и не станет симметричным на практике. Здесь число слагаемых n = 104
Высшие моменты
На критерий жирнохвостости можно смотреть как на применение закона больших чисел к высшим моментам и их сходимости. Можно посмотреть, как ведет себя кумулятивное среднее p-того момента, аналогично рисункам 1–6 для закона больших чисел, только применительно не к самой случайной величине X, а к ее степени Xp (или к степени центрированной X). Чтобы узнать, срабатывает ли закон больших чисел, смотрим, приводит ли добавление наблюдений к сокращению изменчивости среднего (или дисперсии, если она существует). Когда момент не существует, мы увидим случайные скачки, То есть, даже большие выборки выдают разное среднее. Когда момент существует, добавление наблюдений приведет рано или поздно к тому, что скачки прекратятся.
Еще один наглядный метод — посчитать вклад максимального наблюдения в общую сумму и посмотреть, как он ведет себя с ростом n. Такой график называется MS, от maximum to sum.
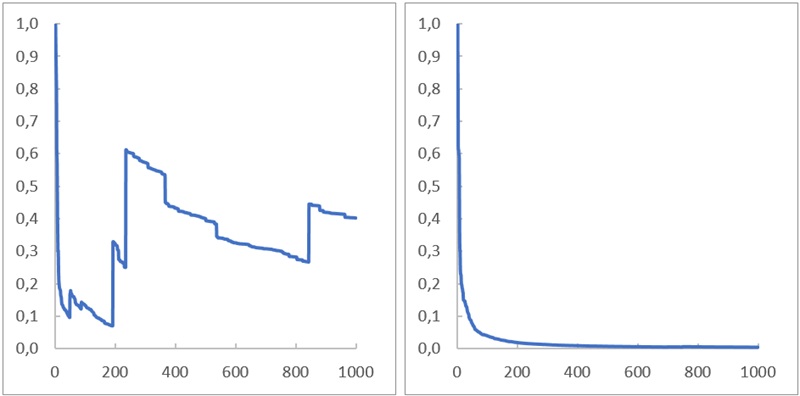
Рис. 7. По оси абсцисс – число наблюдений, по оси ординат – вклад максимального наблюдения в накопленную сумму; слева распределение Коши для х > 0; справа распределение Гаусса для х > 0
Показатель жирнохвостости k
Известны два основных показателя жирнохвостости: (1) показатель хвоста в классе степенного закона и (2) эксцесс для распределений с конечными моментами. Эти показатели применимы не ко всем распределениям и не позволяют сравнивать данные из разных классов и систем параметров.
Как сравнить распределение Парето с хвостом α = 2,1 (с конечной дисперсией), и гауссово? Стандартных способов сравнить эти распределения нет. Показатели, основанные на высших моментах, такие как эксцесс, не подходят, поскольку эксцесс для распределения Парето с хвостом α = 2,1 бесконечно большой.
Есть разные способы, как определить жирные хвосты и ранжировать распределения согласно тому или иному определению. В узком классе распределений, у которых все моменты конечные, критерием служит эксцесс — по эксцессу легко сравнивать отличие того или иного распределения от гауссова, служащего нормой.
Для класса степенного закона критерием может служить показатель хвоста. Кроме того, можно использовать экстремальные значения и найти вероятность превысить максимальное значение с поправкой на масштаб (этот подход практикуется в теории экстремальных значений).
На практике жирнохвостость должна оценивать концентрацию случайной величины в важнейших наблюдениях, отвечая на вопрос: какой вклад вносит в статистические параметры одно-единственное наблюдение? Или в другой формулировке, с поправкой на масштаб: какая доля национального богатства сосредоточена в руках самого богатого жителя?
Талеб предлагает показатель k, позволяющий сравнивать суммы n независимых величин любых распределений с конечным первым моментом. Метод основан на скорости сходимости суммы из n слагаемых к закону больших чисел.
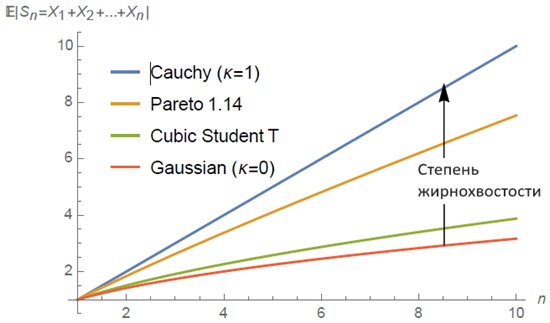
Рис. 8. Интуитивное представление о том, что измеряет k: как растет среднее отклонение суммы одинаковых независимых случайных величин Sn = X1 + Х2 + … + Хn с ростом выборки и как можно доасимптотически сравнить распределения разных классов
Талеб использует следующий критерий, который можно сопоставить с концентрацией: сколько дополнительных данных (при таком-то распределении вероятностей) помогут повысить устойчивость наблюдаемого среднего? Эта задача имеет смысл не только в статистике. Ее можно понять и так: насколько диверсификация ценных бумаг в структуре портфеля (при неизменной общей стоимости портфеля) повысит его устойчивость?
Показатель k отличается от асимптотических показателей (в частности, от тех, что используются в теории экстремальных значений) тем, что является по своей сути доасимптотическим. Это важное преимущество. В реалистичных моделях асимптота не достигается.
Показатель k дает следующее:
- Позволяет сравнивать суммы n величин, когда у них разные распределения при заданном числе слагаемых или одинаковое распределение при разных n, и оценить доасимптотические свойства заданных распределений.
- Дает меру расстояния до предельного распределения, а именно до бассейна устойчивости по Леви (которому, в частности, принадлежит гауссово распределение).
- Для статистических выводов позволяет оценивать скорость срабатывания закона больших чисел как скорость изменения абсолютной погрешности математического ожидания, оцениваемого по выборочному среднему, при увеличении размера выборки n.
- Позволяет оценивать сравнительную жирнохвостость двух разных одномерных распределений, имеющих конечный первый момент.
- Позволяет заранее узнавать, сколько раз потребуется повторить обсчет для моделирования по методу Монте-Карло.