Новая книга Нассима Николаса Талеба посвящена статистическим распределениям, от которых можно ждать экстремальных событий. Книга математическая, и её выход в неспециализированном издательстве тиражом 4000 экз. вызывает удивление. Наверное, издатель решил, что под впечатлением от предыдущих книг Талеба и эту раскупят. Моих знаний математики явно недостаточно, и я ограничился чтением нетехнических разделов и моделированием в Excel некоторых представленных закономерностей. Мои комментарии набраны с отступом.
Нассим Николас Талеб. Статистические последствия жирных хвостов. – М.: КоЛибри, Азбука-Аттикус, 2023. – 480 с.

Скачать заметку в формате Word или pdf, примеры в формате Excel (файл весит 45М так как содержит массив случайных чисел 1М строк)
Купить бумажную книгу в Ozon или Лабиринте, в цифровом формате книга не выходила
Чем хуже вы понимаете мир, тем проще вам принять решение.
Эта книга состоит из (1) опубликованных статей и (2) бесцензурного комментария, посвященных тем классам статистических распределений, от которых можно ждать экстремальных событий. Мы изучим, как использовать эти распределения для статистических выводов и принятия решений.
«Стандартная» статистика работает на основе теорем, выведенных для тонких хвостов. Чтобы работать с жирными хвостами эти методы придется либо адаптировать нетривиальным образом, либо вовсе исключить из арсенала полезных инструментов.
Автор обогатил свой опыт, когда осуществил программу научных исследований и выпустил ряд книг серии Incerto, посвященных выживанию в реальном мире с его структурой неопределенности, которая слишком сложна для нашего понимания: Одураченные случайностью, Черный лебедь. Под знаком непредсказуемости, О секретах устойчивости, Антихрупкость. Как извлечь выгоду из хаоса, Рискуя собственной шкурой.
Цикл Incerto ставит целью объединить пять областей знания, связанных с жирными хвостами и экстремальными событиями: в математике, философии, общественных науках, теории контрактов и теории принятия решений, — с опытом профессионалов. Если вы спросите, при чем здесь теория контрактов и теория принятия решений, то ответ таков: математика опционов основана на идее условной вероятности и объединении контрактов с целью изменить класс воздействия в хвостах распределения; некоторым образом теория опционов — это математическая теория контрактов. Теория принятия решений ставит целью не понять мир, а выбраться из неприятностей и выжить. Этой задаче будет посвящен следующий том Технического Incerto, его текущее рабочее название — Convexity, Risk, and Fragility («Выпуклость вниз, риск и хрупкость»).
Глава 3. Нетехнический обзор – лекция в колледже Дарвина
В этой главе кратко изложены все основные идеи проекта жирных хвостов. В первую очередь, список последствий, которые жирные хвосты имеют для статистических выводов.
О различии между тонким и жирным хвостом
Представим два воображаемых царства:
- Медиокристан (тонкие хвосты), как только выборка изучаемых событий станет большой, дальнейшие наблюдения перестанут влиять на оценку статистических свойств.
- Экстремистан (толстые хвосты), где на статистические свойства непропорционально сильно влияют редкие события (хвосты).
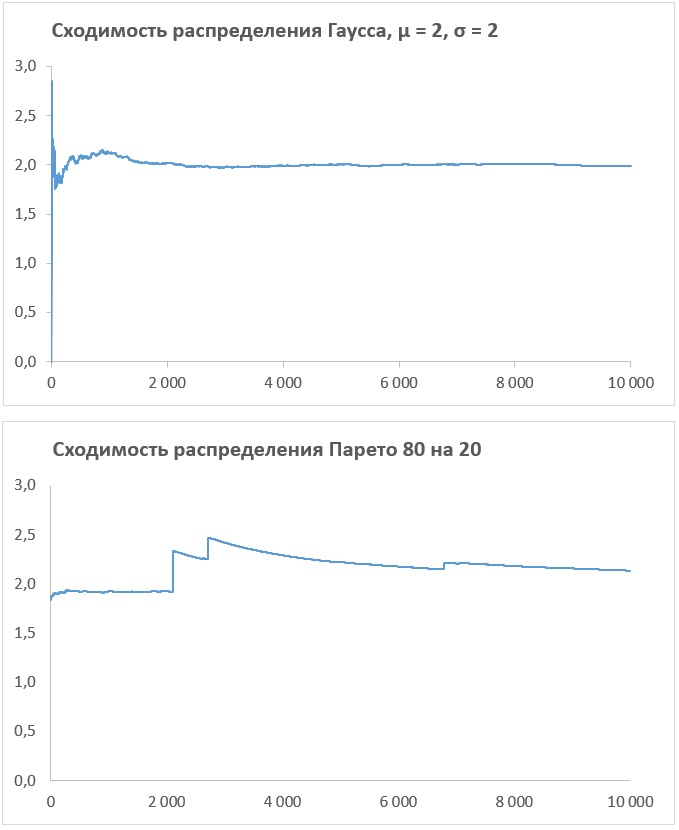
Рис. 3.1. Закон больших чисел, то есть сходимость среднего по выборке к устойчивому значению, медленно работает в Экстремистане; по оси абсцисс – число итераций n, по оси ординат – среднее значение после n итераций
В примере взято распределение со степенным законом при показателе хвоста α = 1,13, обеспечивающем правило Парето 80 на 20. В обоих распределениях одно и то же среднеквадратическое отклонение.
Нижняя кривая на рис. 3.1 построена на основе обратного распределения Парето
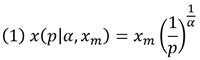
где x – случайная величина, распределенная по Парето, p – вероятность, α – параметр масштаба (определяет форму распределения), xm – параметр смещения (определяет минимальное значение).
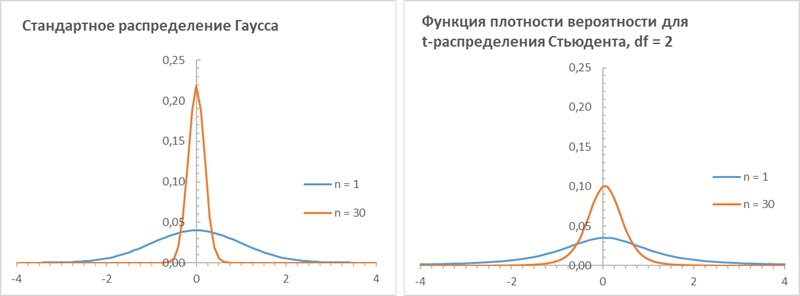
Рис. 3.2. Что происходит с распределением среднего по выборке при росте числа наблюдений? Представлен тот же феномен, что на рис. 3.1, но в пространстве вероятностных распределений. Сжать распределение с жирным хвостом труднее, чем гауссово. Выборка потребуется гораздо большая.
t-распределение Стьюдента с df = 1, оно же стандартное распределение Коши, относится к классу устойчивых, т.е., не изменяет свой вид при переходе от единичных наблюдений к выборкам. Результаты моделирования методом Монте-Карло для 100 000 итераций:
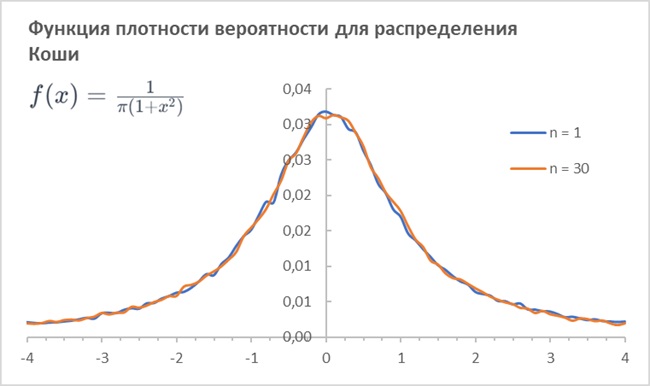
Рис. 3.2а. Никакое увеличение размера выборки не сжимает распределение Коши
Рассмотрим большое отклонение K:
- В Медиокристане вероятнее два раза подряд встретить в выборке отклонение больше K, чем один раз – отклонение больше 2K.
- В Экстремистане скорее попадется отклонение выше 2K, чем два раза подряд отклонение выше K.
Пусть в Медиокристане мы выбрали двоих жителей, и оказалось редкий, хвостовой случай, что их суммарный рост 4,1 метра. При гауссовом распределении самое вероятное сочетание окажется 2,05 и 2,05. Никак не 10 сантиметров у одною жителя и 4 метра у другого.
Вероятность отклониться дальше чем на 3σ составляет 0,00135, а вероятность отклониться дальше чем на 6σ, то есть вдвое сильнее, составляет 9,86*10-10. Значит, вероятность совпадения двух трехсигмовых событий равна 0,00135*0,00135=1,8*10-6 и это гораздо вероятнее, чем одно шестисигмовое событие.

Рис. 3.3. Расчеты в Excel для этого примера
На рис. 3.4 показано, чем дальше мы продвигаемся по хвосту, то есть, чем больше K, тем более вероятно, что событие произойдет из-за двух независимых аномалий размером K.
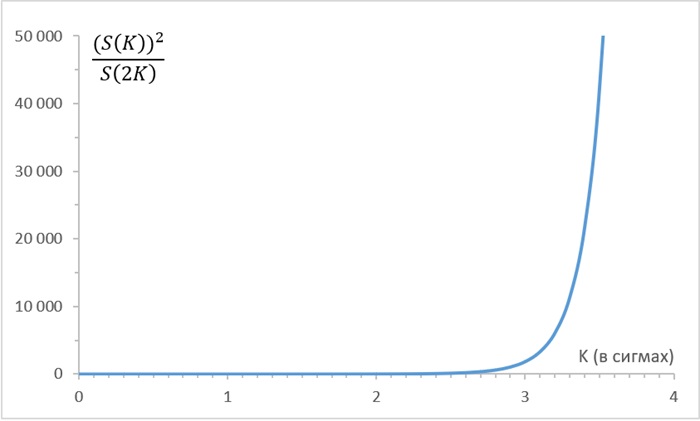
Рис. 3.4. Отношение функций выживания S() для двух аномалий размером K и одной аномалии размером 2K для гауссовского распределения
Теперь отправимся в Экстремистан и выберем двух жителей. Пусть оказалось, что в сумме их состояние составляет 36 млн. долларов. Но вряд ли это будет сочетание 18М+18М. Скорее окажется, что это 35 999 000 и 1000 долларов.
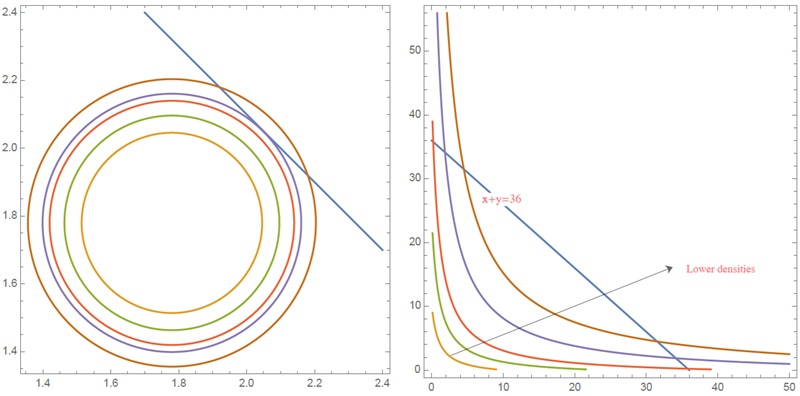
Рис. 3.5. Изолинии плотности вероятности для двух независимых распределений: а) гауссианы, прямая показывает случай x + y = 4,1, самый вероятный случай x = y = 2,05; б) толстые хвосты (степенной закон), прямая показывает случай x + y = 36, самые вероятные случаи x близко к 36, y около нуля и y близко к 36, х около 0
Мы подчеркнули четкое различие между двумя областями. В классе субэкспоненциальных распределений катастрофа скорее наступит из-за одного редкого события, чем из-за серии аварий. Эта логика лежит в основе классической теории рисков, намеченной страховым статистиком Филипом Лундбергом в начале XX века и формализованной в 1930-е Харольдом Крамером, но забытая современными экономистами. Чтобы имело смысл страховать убытки, у них должно быть много ожидаемых причин, а не одна-единственная: только при большом числе ожидаемых причин возможна диверсификация.
Это показывает, что страховой бизнес работает только в Медиокристане; не выписывайте страховки без верхнего предела возмещаемою ущерба, если рискуете разориться на одной-единственной катастрофе. Это правило называется принципом катастрофы. Принцип катастрофы эквивалентен следующему критерию су6экспонснциальности хвоста распределения: если такому распределению следуют независимые случайные величины Х1, Х2, …, Хn, то Р(Х1 + Х2 + … + Хn > x) → P(max{ Х1, Х2, …, Хn} > x) при x → ∞.
Самый жирный хвост – это когда в распределении всего одно отклонение, зато огромное, а не многочисленные умеренные аномалии. Если взять распределение вроде гауссова и начать ужирнять его хвосты, число событий за пределами одного стандартного отклонения падает. При гауссовом распределении вероятность того, что случайное событие попадет в интервал плюс-минус одного стандартного отклонения от математическою ожидания, составляет 68%. По мере ужирнения хвостов, скажем, до уровней, типичных для финансовых рынков, вероятность того, что событие останется в пределах одного стандартного отклонения от математического ожидания, возрастает до 75-95%. Чем жирнее хвосты, тем выше и уже пик и вместе с тем сильнее эффект очень больших отклонений. Поскольку сумма всех вероятностей дает 1 (даже во Франции), при добавлении жира в хвосты худеют склоны пика.
Хвост, виляющий собаками: интуитивно
Чем толще хвост распределения, тем больше хвост виляет собакой, то есть важная информация сосредотачивается в хвосте, покидая «туловище» (центральную часть) распределения. В случае очень жирного хвоста все отклонения, кроме больших, делаются информационно стерильными.
Центр становится просто шумом. Хотя «доказательная наука» еще не вполне осознала этот феномен, но есть обстоятельства, когда основной корпус данных ни о чем не свидетельствует. Это свойство также объясняет, почему закон больших чисел медленно срабатывает при наблюдении таких областей, ведь хвостовые наблюдения, где сосредоточена главная информация, по определению случаются редко.
Это свойство объясняет, например, почему наблюдение миллиона белых лебедей не доказывает несуществование черных лебедей или почему миллион подтверждающих наблюдений стоит меньше, чем одно опровергающее.
Оно также объясняет, почему нельзя сопоставлять случайные величины, определяемые своим хвостом (например, число жертв пандемии), со случайными величиями, определяемыми своим телом (например, число утонувших в своем бассейне.
Дополнительные категории и что из них следует
Рассмотрим разные степени толстохвостости. Упорядочим их по серьезности. Распределения бывают:
Толстохвостые ⊃ Субэкспоненциальные ⊃ По степенному закону (по Парето)
Чтобы попасть в толстые хвосту достаточно всего лишь быть толще, чем у гауссова распределения; это значит, что в пределы ±пределы ± среднеквадратическое отклонение должно попасть больше чем 68,2% наблюдений, или что эксцесс превышает 3.
Момент порядка р случайной величины X — это математическое ожидание p-той степени случайной величины X, т. е. E(ХР). Однако центральный момент порядка р — это математическое ожидание p-той степени не самой случайной величины X, а разности Х – EХ, т. е. μр = E(Х – EХ)Р.
В русской литературе коэффициентом эксцесса называют величину
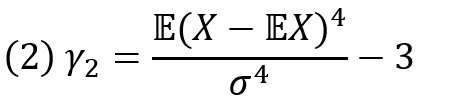
где E(X-EX)4 – 4-й центральный момент и σ – среднеквадратическое отклонение случайной величины X. В английской литературе эксцессом (kurtosis) называют
![]()
Распределению с самым малым куртозисом, 1, следует случайная величина, принимающая только два значения, причем с равной вероятностью. Представляя эти значения как μ ± σ, получаем среднее σ и среднеквадратическое отклонение σ.
Для произвольной случайной величины X со средним μ и среднеквадратическим отклонением σ эксцесс оценивает рассеяние случайной величины X вокруг двух значений, μ ± σ. Распределение с одним горбом может иметь большой эксцесс в двух случаях: (1) если большая масса сосредоточена в узком пике вблизи μ или (2) если большая масса находится в хвостах х ≪ μ–σ и х ≫ μ+σ. Строгая формула
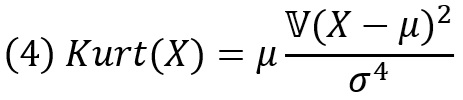
Здесь величина (X–μ)2 имеет среднее σ2, и дисперсия этой величины оценивает ее рассеяние вокруг σ2 и, тем самым, рассеяние величины X вокруг двух значении μ ± σ.
Субэкспоненциальные распределения не вошедшие в класс степенного закона, хвост лишь умеренно толст и не ставит распределение под чудовищное, непропорциональное воздействие со стороны редких событий. У субэкспоненциального распределения в наличии все статистические моменты.
Распределения третьего уровня называют по-всякому — степенной закон, правильно меняющийся класс, класс «с хвостом Парето». Но и среди таких различают разную жирность. У всякого жирнохвостого распределения некоторый статистический момент обращается в бесконечность, и все моменты более высоких порядков также бесконечны.
Рассмотрим пирамиду на рис. 3.7. Слева внизу вырожденное распределение, когда случайная величина может принимать только одно значение. Этажом выше распределение Бернулли, при котором возможны ровно два исхода. Еще выше два гауссовых распределения. Естественное гауссово распределение (с носителем от минус до плюс бесконечности) и приближения, полученные сложением случайного блуждания (с более-менее компактным носителем, если не допустить бесконечно большого числа слагаемых). Это две разные вещи, ведь первое разрешает бесконечно большие значения, втрое — нет (не считая асимптотического приближения к бесконечным значениям).
Над гауссовыми распределениями расположен класс субэкспоненциальных, не принадлежащих классу степенного закона. В субэкспоненциальном классе у распределения существуют все моменты. К этому классу относятся логнормальные распределения. При низкой дисперсии они тонкохвостые; при высокой дисперсии обнаруживают ярко выраженное толстохвостое поведение. Некоторые спешат обрадоваться, когда данные оказываются распределены не по Парето, а логнормально, однако иногда радоваться не стоит.
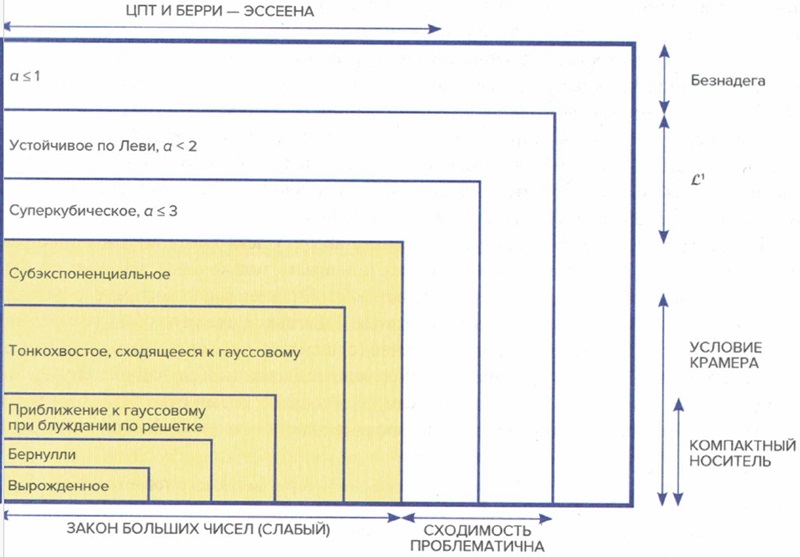
Рис. 3.7. Пирамида толстых хвостов и ряд классификаций по сходимостям (сходимость по закону больших чисел и др.) и по серьезности проблем для выводов. Распределения по степенному закону на белом фоне, остальные на желтом
Принадлежность субэкспоненциальному классу не обеспечивает условия Крамера, разрешающего заниматься страхованием (см. рис. 3.4). Говоря техничнее, условие теоремы Крамера означает существование математического ожидания для экспоненты случайной переменной.
Покинув желтую зону, где закон больших чисел (ЗБЧ) более-менее работает, мы перейдем в классы, где не будет работать центральная предельная теорема (ЦПТ) и начнутся проблемы со сходимостью. Это зона степенных законов. Мы ранжируем их по показателю хвоста α; чем ниже показатель хвоста, тем жирнее хвост. При α < 3 распределение называется субкубическим и при α = 3 — кубическим. Эта часть жирнохвостой зоны неформально приграничная: у распределений есть моменты первого и второго порядка, а значит, закон больших чисел и центральная предельная теорема применимы… теоретически.
Следом идет класс с α < 2, который мы условно называем классом устойчивости по Леви. Еще выше по пирамиде жирность хвоста усиливается и пропадает дисперсия. При 1 ≤ α ≤ 2 дисперсии нет, но еще существует абсолютное среднее отклонение (то есть математическое ожидание абсолютной величины отклонения).
Еще выше, в верхней секции, пропадает даже математическое ожидание. Мы назвали этот класс Безнадегой. Если вы что-то увидели в потоке данных этой категории, вернитесь домой и никому не рассказывайте.
У статистиков сложилась традиция в отношении толстых хвостов: пообещать, что будут использоваться особые распределения, а потом как ни в чем не бывало опять использовать старые показатели, критерии и оценки значимости. Но после выхода из желтой зоны, для которой раньше разрабатывались статистические методы, ничто не работает по плану.
Обзор проблем со злоупотреблением стандартной статистикой
Статистическая оценка основана на двух элементах: на центральной предельной теореме (предполагающей работу с «большими» суммами, когда почти всякое явление в мире становится уютным и нормальным) и на законе больших чисел, согласно которому дисперсия оценки падает по мере роста выборки. К сожалению, не все так просто; есть ограничения. Нужная выборка сильно зависит от того, какому распределению следует исходный процесс, и драматически различается даже в одном классе. Распределения с конечной дисперсией даже при бесконечных высших моментах могут сходиться, с ростом числа слагаемых n, к гауссовому в центральной части, но не в хвостах. А многие свойства определяются как раз хвостами.
Но что, если мы не успели достичь нормального распределения, если жизнь настигла нас до выхода на асимптоту? Вот о чем рассказывается в данной книге!
Основные следствия и как они связаны с данной книгой
Некоторые следствия выхода за пределы желтой части пирамиды, зоны статистического комфорта.
Закон больших чисел в реальном мире даже если работает, то слишком медленно
Поведение суммы или последовательности, когда n велико, но не бесконечно, мы называем предасимптотикой. Это одна из центральных тем этой книги.
Среднее по выборкам редко концентрируется вокруг среднего, присущего генерирующему процессу
Чаще проявляется смещение среднего по малой выборке к меньшим значениям. Ни при каком толстохвостом распределении невозможно правильно оценить среднее генеральной совокупности по среднему выборки — первое зависит от редких событий, а такие события становятся видны только при большом объеме данных. При законе 20 на 80, в 92% наблюдений по выборке среднее занижается. Чтобы на основании среднего по выборкам можно было судить о распределении, требуются объемы данных на порядки больше, чем практически доступный объем (исследователи в области экономики до сих пор этого не понимают, хотя трейдеры инстинктивно чувствуют).
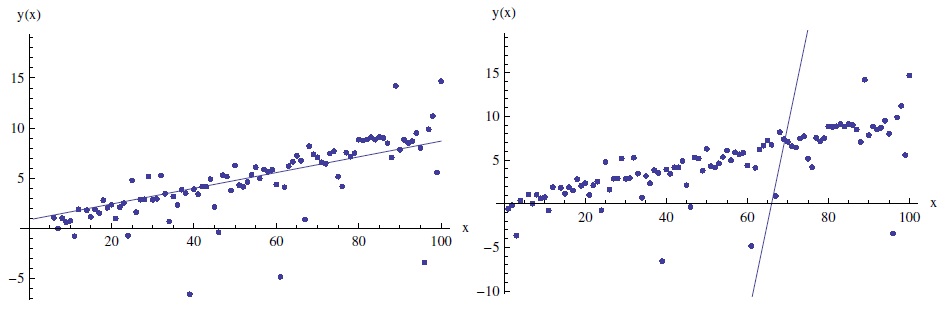
Рис. 3.8. При наличии толстого хвоста можно подогнать весьма различные линейные регрессии к одним и тем же данным (а теорема Гаусса — Маркова[1], на которую опирается метод линейной регрессии, неприменима). Слева: обычная (наивная) регрессия. Справа: линейная регрессия, которая пытается адаптироваться к большой дисперсии — так сказать, домножить на хеджирующий коэффициент, то есть защитить агента от большого отклонения, идя на худшее приближение слабых отклонений. Иногда фатально именно пропустить большое отклонение. Заметим, что выборка не содержит критических наблюдений, об их существовании лишь делаются допущения методами теневого среднего.
Среднее генеральной совокупности – это среднее выборки, если бы мы могли выбрать всю генеральную совокупность целиком. Среднее по выборке – это то, чем мы располагаем на практике. Даже в случаях, когда собраны данные по всей существующей на текущий момент генеральной совокупности – например, о благосостоянии населения или военных потерях, – среднее по этим данным может не совпасть со средним, отвечающим механизму генерирования данных. Последнее называют теневым средним.
Такие показатели, как среднеквадратическое отклонение и дисперсия, неприменимы
Выборка не отражает их, даже если по выборке их можно рассчитать. Научный предрассудок, будто концепция среднеквадратического отклонения – универсально полезный показатель вариативности.
Бета-коэффициент, коэффициент Шарпа и прочие финансовые показатели неинформативны
Бета-коэффициент показывает, насколько изменится актив А в ответ на изменение на рынке в целом; вычисляется как отношение ковариации между А и рынком к дисперсии рынка. Коэффициент Шарпа показывает среднюю или избыточную доходность актива или стратегии, деленную на её среднеквадратичное отклонение.
Для этих показателей либо требуется слишком много данных, на много порядков величины больше имеющегося объема, либо исходная модель нужна не та, что используется, а другая, которую еще не изобрели. На рис. 3.9 показано, как коэффициент Шарпа, разработанный, чтобы предсказывать эффективность, провалился по выборке и даже сработал обратно своему назначению. То, что такой показатель по-прежнему используется, демонстрирует, кик легко люди ведутся на цифирь.
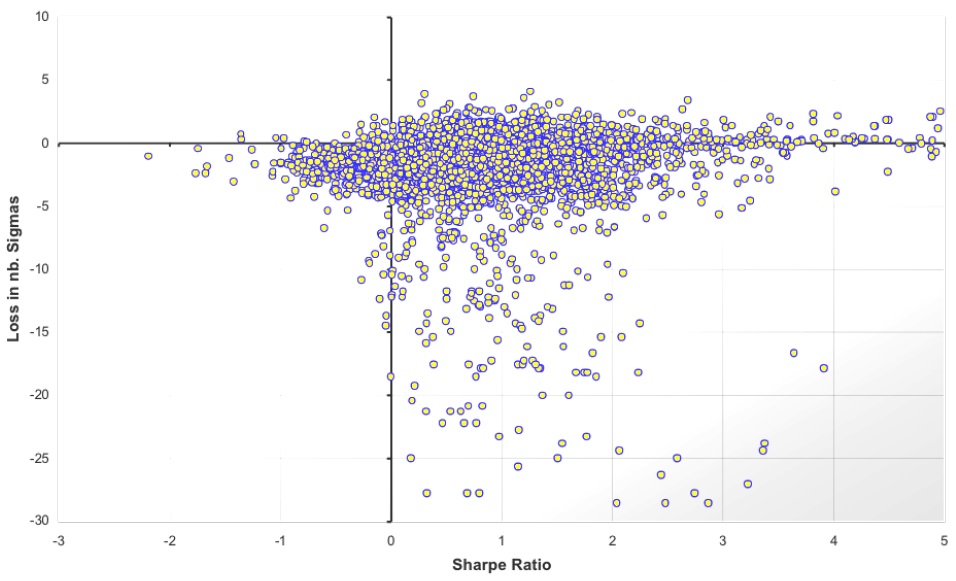
Рис. 3.9. Данные о хедж-фондах: по горизонтали коэффициент Шарпа накануне кризиса 2008 года, по вертикали потери в период кризиса, в среднеквадратичных отклонениях. Коэффициент Шарпа не предсказал эффективность хедж-фонда в выборке.
Практически каждая экономическая величина и стоимость ценных бумаг имеет толстый хвост. Из 40 000 изученных ценных бумаг ни одна не оказалась тонкохвостой. В этом главная причина неудач в финансах и экономике.
Финансовые теоретики делают безосновательные заявления вроде «если у распределения толстый хвост, но существуют математическое ожидание и дисперсия, то портфельная теория на основе среднего и дисперсии работает». Беда в том, что даже когда дисперсия существует, мы не имеем сколько-нибудь точного представления о ее величине; будучи вторым статистическим моментом, дисперсия подчиняется закону больших чисел еще медленнее, чем среднее, потому что имеет еще более толстый хвост, чем исходная случайная величина.
Робастная статистика не робастна, а выборочное распределение не эмпирично
Робастная статистика гонится за параметрами, которые слабо реагируют на хвостовые события, наблюдения больших значений. Такое понимание робастности порочно, потому что отсутствие реакции показателя на хвостовое событие вполне может быть следствием неинформативности этого показателя. Более того, такие параметры не помогут оценить ожидаемый платеж.
Робастная статистика строится в рамках непараметрической ветви статистической науки, где исследователи мнят, будто без параметров анализ будет меньше зависеть от распределения. На протяжении всей этой книги будет демонстрироваться, что зависимость от распределения только обостряется.
Устраняя выбросы, вы уродуете процесс сходимости к матожиданию и, по сути, сокращаете доступные данные. Часто бывает полезно перепроверить достоверность выброса – вдруг это случайная ошибка, такая как опечатка или компьютерный глюк. В непараметрической статистике популярно выборочное распределение, которое не работает эмпирически, поскольку неправильно представляет ожидаемые платежи.
Допустим планируется построить систему дамб для защиты от наводнения. Данные по уровню воды покажут наихудшее в истории наводнение, и этот уровень будет историческим максимумом. Наивно построенное выборочное распределение предскажет, что вероятность более страшного наводнения ноль (или около того). Но… в том году, когда случился исторический максимум, он превзошел предыдущий исторический максимум. И если бы к тому году мы столь же наивно построили эмпирическое распределение по имевшимся данным, мы не предвидели бы явление нового исторического максимума. При толстом хвосте различие между историческим максимумом и ожидаемым максимумом мною драматичнее, чем при тонком хвосте.
Такой вещи, как типичное большое отклонение, не существует
При условии «большого» изменения величина изменений расходится, особенно при серьезной толщине хвоста (класс степенного закона). В Гауссовом мире математическое ожидание изменения величина которого больше 4σ, примерно 4σ. При степенном законе – в разы больше. Мы называем это свойством Линди.
Прогнозирование в пространстве частот расходится с ожидаемым платежом
Львиная доля утверждений в литературе по психологии и по принятию решений, где говорится о якобы переоценке вероятностей в хвосте и якобы иррациональном поведении из-за редких событий, делается из-за непонимания исследователями природы хвостового риска, смешения вероятности и ожидаемого платежа, злоупотребления распределениями вероятностей.
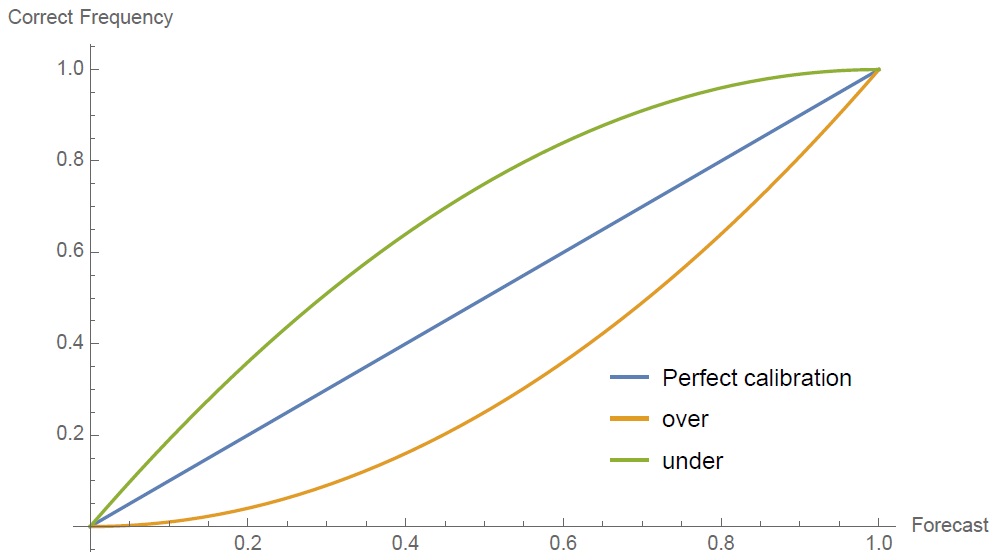
Рис. 3.12. Калибровка вероятностей, встречаемая в литературе по психологии. На оси х показана оценка вероятности, данная прогнозистом, а на оси у — что происходит в действительно. Например, если после того, как некий метеоролог объявил вероятность дождя 30%, дождь происходит именно в 30% случаев, оценка этого метеоролога объявляется «откалиброванной». Мы утверждаем, что калибровка в пространстве частот (вероятностей) — академическая тема (в плохом смысле), создающая неверное представление о реальной жизни за пределами узкой области пари о двух возможных исходах.
Дурацкая идея сфокусироваться на частотах вместо математического ожидания может дать небольшой эффект, но только при тонком хвосте, никак не при толстом.
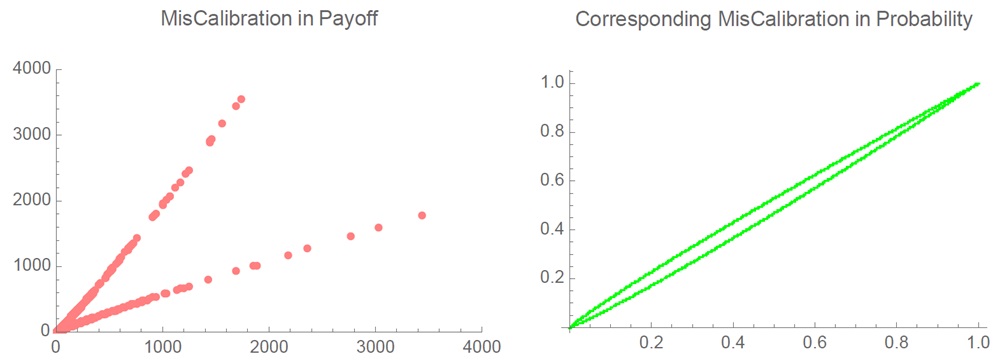
Рис. 3.13. Как ошибка калибровки по вероятности отвечает ошибке калибровки по платежу при степенном законе. Рассматривается распределение Парето с показателем хвоста α = 1,15
Неточный прогноз вероятности («ошибка калибровки») лежит в другом классе распределений вероятности, нежели колебания прибылей и убытков в реальном мире (или чистых платежей). «Калибровка» (мера точности) при прогнозе вероятности принадлежит пространству вероятностей, то есть диапазону от 0 до 1. Всякая стандартная мера этого рода обязательно имеет тонкий хвост – даже когда случайная ветчина, в отношении которой делается прогноз, имеет толстый хвост. Платежи в реальном мире, напротив, могут иметь толстый хвост, и у их «калибровки» свойства распределения должны следовать свойствам распределения случайной величины.
Закон больших чисел
Он утверждает, что по мере накопления наблюдений среднее значение становится все более устойчивым. Чтобы увидеть главное различие между Медиокристаном и Экстремистаном, рассмотрим такое событие, как авиакатастрофа. Последствия тяжелые, много погибших; допустим, от 100 до 400. Даже одно такое событие – трагедия. В рамках прогнозирования и управления рисками мы стараемся минимизировать такую вероятность, сделать ее пренебрежимо малой.
А теперь представим себе катастрофу, которая убивает всех, кто когда-либо летал самолетом, даже в далеком прошлом, всех. Считать ли ее событием того же типа? Такого рода события известны в Экстремистане, и, работая с ними, фокусируются не на снижении вероятности события, а на снижении его величины.
- Для первого типа управление рисками состоит в том, чтобы снизить вероятность, то есть частоту, происшествий. Мы подсчитываем число событий и стараемся его уменьшить.
- Для второго типа мы стараемся уменьшить масштаб катастрофы, если она все-таки разразится. Мы заняты не числом событий, а ущербом от одного события.
Если пример показался вам странным, примите во внимание, что центральные банки потеряли в 1982 году больше денег, чем заработали за всю свою историю, и что в 1991 году та же участь постигла в США ссудо-сберегательную отрасль (ныне не существующую), а в 2008–2009 годах вся американская банковская система потеряла все нажитое до последнего пенни.
Эпистемология и дедуктивная асимметрия
Асимметрия в распределениях: скорее преступник постарается выдать себя за честного человека, чем честный человек – выдать себя за преступника. Аналогичным образом легче принять жирнохвостовое распределение за тонкохвостое, чем тонкий хвост за жирный.
Эпистемология: невидимость генератора
Наблюдаемо не вероятностное распределение, а только его реализация. Зная свойства некоторого вероятностного распределения, невозможно утверждать, что ему принадлежит известная реализация. Для обсуждения хвостовых событий требуется метавероятностное распределение (т. е. распределение условных вероятностей того, что случайная величина следует тому или иному вероятностному распределению).
Увидев событие в 20 сигм, мы можем исключить тонкохвостость распределения. Не увидев ни одного большого отклонения, мы не можем исключить толстый хвост, если не знаем порождающего принципа. Можно ранжировать возможные распределения, и по мере наблюдения отклонений исключать распределения одно за другим. Ранг отвечает способности распределения проявлять хвостовые события. Логика следующая: когда кажется, что произошло 10-сигмовое событие, скорее всего, это не событие 10-сигмовое, это распределение выбрано не то и сигма посчитана не та. Можно объявить данное распределение толстохвостым, в силу устранения других возможностей. Другое дело, что никакое наблюдаемое распределение нельзя объявить тонкохвостым. Такова принципиальная проблема черного лебедя.
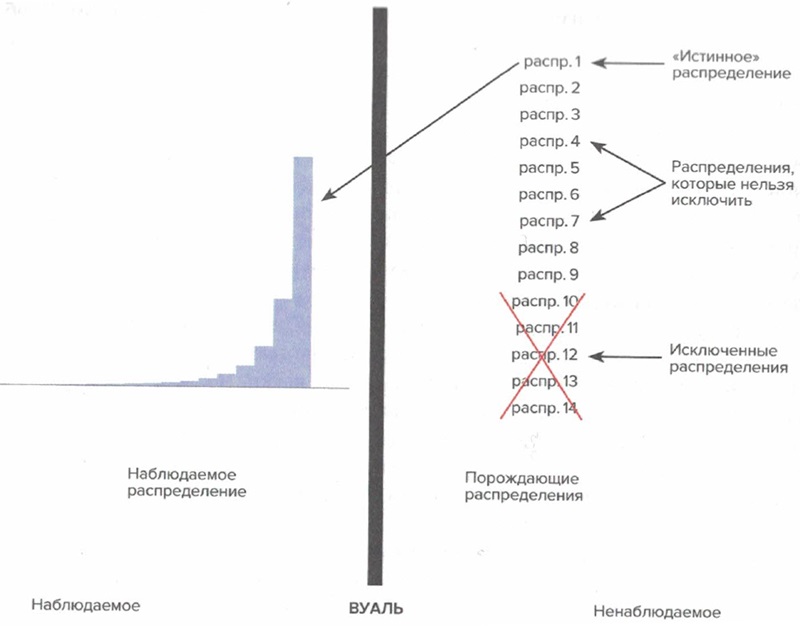
Рис. 3.16. Теоретико-вероятностная вуаль неведения. В мысленном эксперименте с вуалью наблюдатель получает данные, которые производятся помощи генератора временного ряда. Задача наблюдателя: видя только поступающие данные и не зная ничего о порождающем процессе, оценить статистические свойства (вероятностное распределение, среднее, дисперсию, стоимость под риском и т. д.). Понятно, что наблюдатель без доступа к полной информации о генераторе и без надежной теории о принципе, порождающем данные, неизбежно будет ошибаться, но в его ошибках будет некоторая система. Исследовать эту систему — центральная задача в управлении рисками
Карл Поппер дал проблеме индукции асимметричное решение: действовать в негативном стиле – то есть исключать то, что не сработало (подробнее см. Логика научного исследования). Мы распространяем этот подход на статистические выводы с учетом вероятностной вуали и последовательно класс за классом исключаем опровергнутые вероятностные распределения.
Чудесный пример осознания асимметрии мы видим в работах российско-советской школы теории вероятностей – эта асимметрия составляет математическую аналогию идее Поппера. Школа насчитывала три поколения: П.Л. Чебышев, А.А. Марков, А.М. Ляпунов, С.Н. Бернштейн, Е.Е. Слуцкий, Н.В. Смирнов, Л.Н. Большев, В.И. Романовский, А.Н. Колмогоров, Ю.В. Линник, а также новое поколение: В.В. Петров, С.В. Нагаев, А.Н. Ширяев и ряд других.
Они сделали большое дело в истории научной мысли: стали работать не с равенствами. Вместо оценок они нашли границы. Даже для центральной предельной теоремы они построили версии, в которых делалось утверждение о границах. Они ушли далеко вперед по сравнению с нынешним поколением пользователей, мыслящим в терминах точной вероятности. Их метод учитывает скептицизм, рассуждение в одну сторону. Они рассматривали условия не вида А = х, а вида А > х.
Это великий источник для тех, кто работает над интеграцией математической строгости в теорию рисков. Мы всегда знаем только одну сторону – минимальную сумму, которую готовы заплатить за страховку, и не знаем верхней границы.
Философскую проблему перечислительной индукции можно сформулировать как вопрос: Сколько белых лебедей нужно насчитать, прежде чем исключить появление черного лебедя в будущем? Он на удивление точно ложится на вопрос по работе закона больших чисел: Сколько нужно собрать данных, чтобы сделать утверждение с приемлемым уровнем ошибки?
Оказывается, что статистический вывод по самой своей природе основывается на ясном определении и количественном измерении механизма индукции, и в случае толстого хвоста требуется гораздо больше данных. Хотя есть способ измерить относительную скорость индуктивного механизма, сама проблема индукции так и не получает идеального решения.
Наивный эмпиризм: не надо сравнивать Эболу и падения со стремянок
Иногда используют «эмпирические» данные и объявляют, что мы зря тревожимся из-за эболы, от которой за 2016 год умерло всего двое американцев. Объявляют, что больше надо тревожиться из-за смертей от диабета и несчастных случаев, когда человек запутался в простынях. Давайте подумаем в терминах хвостов. Если однажды вы прочитаете в газетах о внезапной смерти 2 млрд человек, что вероятнее: что их убьет эбола или что они погибнут от курения, диабета или простыней?
Не сравнивай толстохвостый процесс в Экстремистане, оказывающий мультипликативное воздействие, и тонкохвостый процесс в Медиокристане.
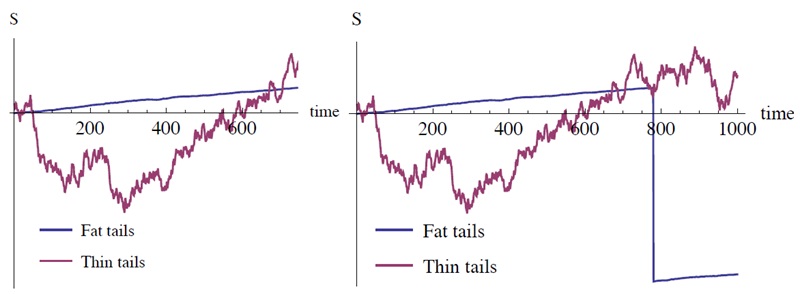
Рис. 3.20. Невозможно «подтвердить» тонкохвостость, но опровергнуть ее можно единственным резким скачком. Спокойные дни не позволяют исключить возможность скачка
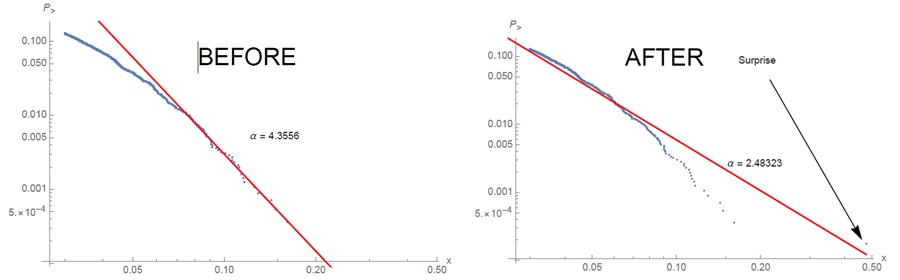
Рис. 3.21. Один день, открывший глаза на истинную природу распределения. Фондовый рынок Аргентины до и после 12 августа 2019. Иногда приходится резко пересмотреть хвосты в сторону утолщения (снизить показатель α); пересмотр в обратную сторону займет долгое время
К сожалению, немногие из зацикленных на доказательной науке осознают (когда пишут статью), как работает эффект хвоста, виляющего собакой. Это наивный эмпиризм — сравнить такие процессы и заявить, что мы слишком беспокоимся об эболе (эпидемиях, пандемиях) и недостаточно о диабете. На самом деле все наоборот. Мы слишком беспокоимся о диабете и недостаточно об эболе и других болезнях с мультипликативным воздействием.
Ошибочное суждение делается из-за непонимания толстых хвостов, которое прискорбным образом ширится. Хуже того, подобные ошибки используются пропагандистами промышленности, которые впаривают нам пестициды и заверяют, что нет причин для беспокойства, потому что в прошлом ущерб был ничтожным.
Корректные рассуждения не приняты в кругах, занимающихся теорией решений и управления рисками; исключение составляют работающие над теорией экстремальных значений и отдел «Адаптивное поведение и познание» в берлинском Обществе Макса Планка, руководимый Гердом Гигеренцером, – эти люди скажут вам, что не стоит игнорировать инстинкты и наставления вашей бабушки; когда ее советы противоречат психологам и теоретикам принятия решений. Обычно бабушкины советы ближе к научной строгости (подробнее см. Герд Гигеренцер. Понимать риски).
Как изменяется масштаб некоторых мультипликативных рисков
«Доказательный подход» слишком примитивен, чтобы работать с эффектами второго порядка (и управлять рисками). Он безусловно нанес огромный ущерб в пандемию COVID-19 и должен быть решительно отвергнут. Одна из проблем состоит в переносе индивидуального риска на коллективный.
В начале пандемии COV1D-19 ряд эпидемиологов, невежественных по части вероятностей, уподобляли риск умереть от этой инфекции риску утонуть в бассейне. Положим, на том этапе это было верно для индивидуума (хотя очень скоро COVID-19 превратился во многих частях страны в главную причину смерти, и в Нью-Йорке достигал уровня 80% всех смертей).
Но с самого начала можно было заметить, что если рассмотреть событие 1000 одновременных смертей, то вероятность приписать их утонувшим в бассейне окажется ничтожной. Причина в том, что COVID у вашего соседа повышает ваши шансы заразиться, тогда как если ваш сосед утонет в бассейне, для вас вероятность утонуть в бассейне не вырастет.
Азбука степенных законов
Обсудим интуицию, стоящую за законом Парето. По-простому он определяется так. Пусть Х – случайная величина, для которой значение х – большое. Тогда отношение вероятности того, что X превысит 2х, к вероятности превысить х, не слишком сильно отличается от отношения вероятности превысить 4х, поделенной на вероятность превысить 2х и так далее. Это свойство называется масштабируемость.
При распределении Парето число людей, владеющих $16M к числу людей, владеющих $8M, такое же, как отношение числа двухмиллионеров к числу миллионеров. Неравенство в богатстве постоянное. У такого распределения нет характерного масштаба, и по-своему оно устроено очень просто. Хотя при таком распределении у случайной величины часто нет среднего и стандартного отклонения, мы неплохо понимаем это распределение. Однако ввиду отсутствия среднего мы не можем обратиться за помощью к учебнику по статистике.
У распределения Парето нет высших моментов: они либо не существуют, либо статистически неустойчивы. Становится понятно, почему экономисты не могут предсказывать события — они пользуются не томи методами и строят неверные доверительные интервалы. Что работает на выборке, не будет работать за пределами выборки. А выборки по определению всегда конечны и всегда имеют конечные статистические моменты. Как объявить дисперсию или эксцесс бесконечными, когда мы не наблюдаем ничего бесконечного в выборке?
Где прячутся скрытые свойства?
Следующее резюмирует все, что я написал в «Черном лебеде». Распределения бывают с одним хвостом (левым или правым) или с двумя. При толстом хвосте редкие события скрыты от наблюдения, и наивный наблюдатель неверно оценивает среднее. Хвостовые события еще внесут свой вклад, но, по определению, они редки.
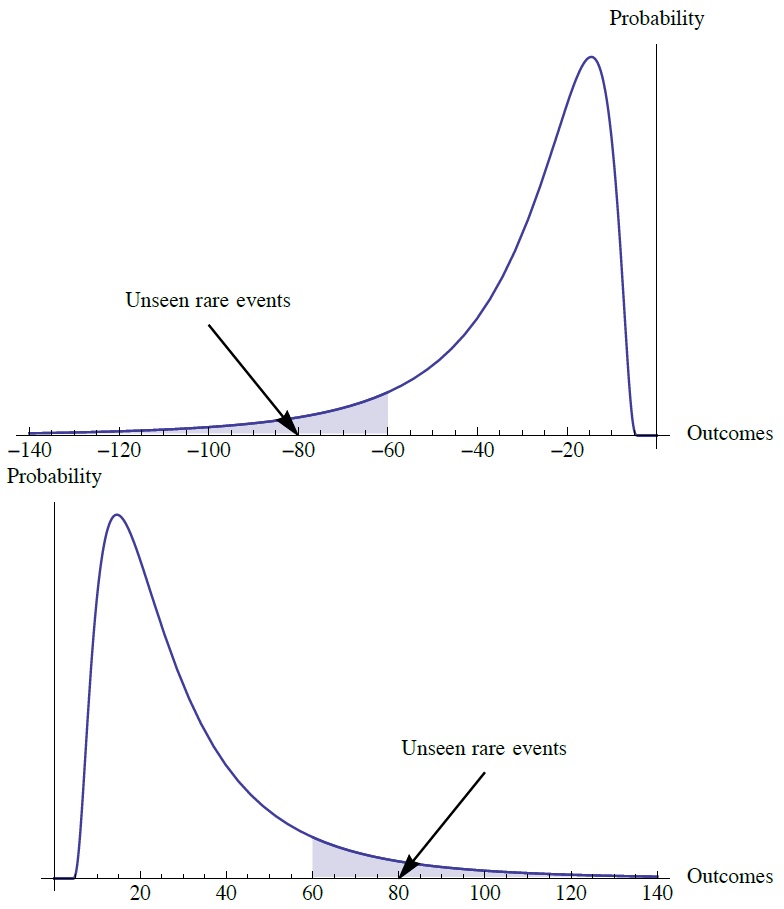
Рис. 3.28. Теневое среднее за работой. Нижний график: обратная проблема индейки — невидимое редкое позитивное событие. Наблюдая позитивно скошенный (антихрупкий) временной ряд и делая выводы о невидимом без учета параметров, вы упускаете из виду хорошее и недооцениваете выгоды. Верхний график: противоположная проблема. Закрашенная область соответствует тому, что мы обычно упускаем в малых выборках, из-за недостаточного числа данных. Интересно, что закрашенная площадь растет с ростом ошибки модели (благодаря выпуклой вниз зависимости хвостовых вероятностей от неопределенности)
Не стоит полагаться на среднее по выборке наблюдений; оно при распределениях с толстым хвостом имеет систематическую ошибку. По этой причине кажется, пока не грянул кризис, что банки приносят большие прибыли. А потом оказывается, что они потеряли все, что имели, и что их приходится выкупать на деньги налогоплательщиков. Чтобы не попадаться в ловушку, мы отличаем истинное среднее (которое я называю теневым) от реализовавшегося среднего.
Вот что мы имеем в виду, когда говорим, что выборочное распределение «не эмпирично». Другими словами: (1) есть разница между атрибутами генеральной совокупности и выборки и (2) даже на исчерпывающие исторические данные следует смотреть как на выборку из более широкого диапазона (прошлое является выборкой; выводы из него являются статистическими суждениями на
Разобравшись в типе распределения, можно оценить математико-статистическое среднее. Оценка будет намного точнее, чем простое измерение среднего по выборке. Так, при распределении Парето 98% наблюдений ниже среднего; наблюдения недооценивают среднее. Но после того, как мы поняли, что имеем дело с распределением Парето, мы можем игнорировать выборочное среднее и использовать другие методы.
Заметим, что исследователи теории экстремальных значений фокусируются на свойствах хвоста, а не на поиске среднего или статистических выводов.
Линейка Витгенштейна: что, это правда было 10-сигмовое событие?
Летом 1998 хедж-фонд с громким названием Long Term Capital Management (Долгосрочное управление капиталом, LTCM) приказал долго жить, разорившись из-за «неожиданных» отклонений на рынках. Это была чувствительная утрата: двое партнеров успели получить премию шведского госбанка, рекламируемую как «Нобелевка в экономике». Фонд привлек многочисленных профессоров финансовой математики и имел подражателей, также привлекших профессоров (и по самому скромному счету, 60 докторов наук разорились в тот период благодаря трейдерам, похожим на LTCM и использующим идентичные методы управления рисками). Минимум двое партнеров выступили с заявлением, что произошло 10-сигмовое событие (отклонение в 10 раз больше среднеквадратического) и что это снимает с них обвинения в некомпетентности (я лично был свидетелем двух таких заявлений).
Давайте применим в этой ситуации подход, который автор называет витгенштейновской линейкой: спросим себя, правда ли мы измеряем линейкой стол, как обычно, или на этот раз мы измеряем столом линейку?
Примем для простоты, что есть только две возможности: гауссово распределение и распределение по степенному закону. При гауссовом вероятность, которую мы определим как функцию выживания для события величиной 10 среднеквадратических отклонений, составит 1 из 1,31 х 1023. Для степенного закона в том же масштабе — t-распределения Стьюдента с показателем хвоста 2, — функция выживания составит 1 из 203.
В Excel t-распределения Стьюдента с показателем хвоста 2 (число степеней свободы df = 2) можно вычислить с помощью формулы =СТЬЮДЕНТ.РАСП.ПХ(х;2), где х = отклонение от среднего в стандартных отклонениях. Подставляем х = 10, получаем =СТЬЮДЕНТ.РАСП.ПХ(10;2) = 202,995
Ну и какова вероятность, что распределение гауссово при условии наблюдения 10-сигмового события и выбора из двух наших альтернатив?
Начнем с правила Байеса…
![]()
… и применим к нашему случаю:
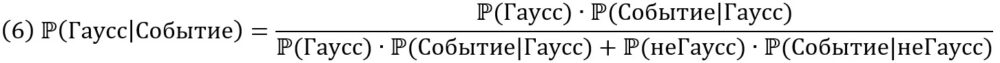
Если до наблюдения была хоть крошечная, 10–10, вероятность того, что распределение не гауссово, после случившегося можно сделать твердый выбор в пользу альтернативы — распределение с толстым хвостом.
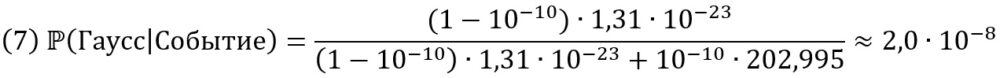
Эвристическое правило: смело отвергайте гипотезу о гауссовости, если случилось хотя бы одно событие > 4σ. Никакие заплатки не дают адекватного результата и должны быть признаны мошенничеством. Великий человек Бенуа Мандельброт крайне критически относился к методам, дополняющим гауссовость разрывами или иными трюками ad hoc, чтобы объяснить, что не так с данными (например, процесс диффузионных скачков Мертона). Задним числом всегда можно подогнать нужные разрывы. Мандельброт цитировал слова, приписываемые Джону фон Нейману: «С четырьмя параметрами я могу подогнать кривую под слона, а с пятью — заставить его вилять хоботом».
X и F(X): как путают воздействие величины Х с самой величиной Х
Рассмотрим случайную величину Х и ее воздействие на вас F(X). В этом разделе F(X) обозначает не функцию распределения случайной величины F(X)=P(X<x), а функцию платежа, или последствий того, что случайная величина X примет значение x.
Практики и венчурные инвесторы часто замечают такое недоразумение: не-практики начинают рассказывать практикам об X, считая, что практикам это интересно, тогда как те думают об F(X) и ни о чем другом. Смешение X с ее последствиями F(X) – хроническая болезнь со времен Аристотеля; она обсуждается в Антихрупкости как главная тема книги.
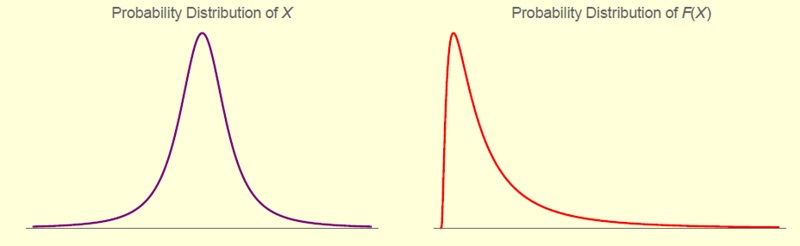
Рис. 3.29. Проблема смешения случайной величины X и ее платежа, F(X). Когда знаешь, что функция F выпукла вниз, подробностями можно не интересоваться. Когда F выпукла вверх, и стоит задача изменить ситуацию, надежнее изменить F, а не X
Величина X может быть показателем безработицы в Сенегале, F1(X) — ее воздействием на итоговый отчет МВФ, a F2(X) — ее воздействием на финансы вашей бабушки (надо полагать, минимальным). X может быть курсом акций, причем вы владеете опционом, и F(X) — воздействие X на стоимость вашего опциона. X может быть изменением вашего богатства, a F(X) — его выпукло-вогнутым воздействием на ваше благополучие. Можно заметить, что F(X) намного устойчивее, или робастнее — то есть имеет более тонкие хвосты, — чем X.
Выпуклые и линейные функции случайной величины X. Рассмотрим рис. 3.30. Чем меньше зависимость F (по вертикали) от X (по горизонтали) похожа на линейную, тем меньше остается общего между вероятностным распределением X и F(X). Даже при небольшой выпуклости F статистические и прочие свойства F(X) отличаются от свойств X. Например, математическое ожидание F(X) отличается от F(𝔼 X) согласно неравенству Йенсена, которое гласит: если функция F(X) выпуклая вниз, то
![]()
При резкой нелинейности F влияние вероятностного распределения X на вероятностное распределение F(X) тает. Мораль: чтобы что-то изменить, фокусируйтесь на F и не гонитесь за измерением трудноуловимых свойств X.
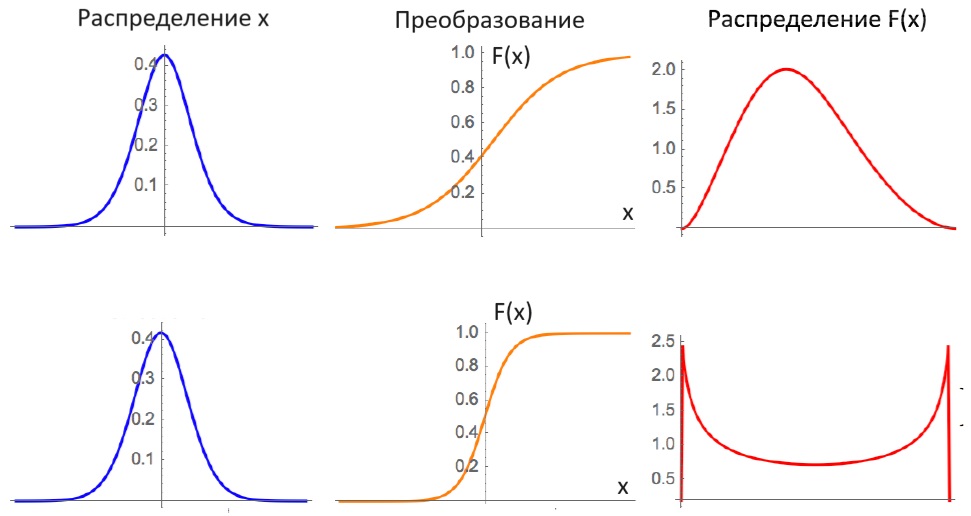
Рис. 3.30. Проблема смешения: S-образная функция F(X) превращает случайную величину X с толстохвостым распределением на бесконечном промежутке (-∞, +∞) в случайную величину F(X) с бесхвостым распределением на промежутке (0, 1). Сильная выпуклость (нижний пример) способна превратить пик в яму с вертикальными стенками на краях, аналогичную арксинусу.
Ограниченные знания
Важно, что ограниченность наших знаний касательно распределения X не обязательно транслируется в неопределенность распределения F(X). Бывает, что мы не управляем X, но можем повлиять на F. Иногда это дает нам весьма существенное влияние на F(X). Опасное заблуждение относительно проблемы черною лебедя — фокусироваться X, пытаться предсказать X. Я пытаюсь всем объяснить, что, даже не понимая X, можно работать с понятным нам F; другие же упорно бьются над предсказанием X – бесплодно, потому что маловероятные события не поддаются расчету, особенно в области толстого хвоста. Между тем итоговое воздействие на нас оказывает как раз F(X).
Вероятностное распределение у F(X) не такое, как у X, когда функция F нелинейная. Чтобы получить F(X) из X, нужно выполнить нелинейное преобразование. Функция F практики всегда нелинейная (лично я не знаю ни одного исключения) и часто S-образная, то есть выпуклая вниз-вверх возрастающая.
Хрупкость и антихрупкость
Когда F выпуклая вверх (хрупкая), ошибки относительно X могут преобразоваться в огромные отрицательные отклонения F(X). Когда F выпуклая вниз, мы защищены от суровых отрицательных отклонений. Если мы действуем методом проб и ошибок или выбираем опцию или опцион, нам важно не столько понимать про случайную величину X, сколько про создаваемые риски. Грубо говоря, статистические свойства X тонут в свойствах F. Книга Антихрупкость посвящена тому, что воздействие X важнее и наивна установка «хочу все знать», то есть понимать X.
Чем сильнее нелинейность F, тем меньше вероятностное распределение X влияет на вероятностное распределение итогового пакета, F(X). Многие авторы путают вероятности тех или иных значений X с вероятностями F(X).
Нужна выпуклость вниз. Осенью 2017 одна фирма обанкротилась, делая ставки по поводу волатильности. Эти люди прогнозировали дисперсию ниже той, что ожидалась рынком… и были правы. Почему же они обанкротились? Потому что использовали выпуклую вверх функцию платежа. Вспомним, что случайная величина X распределена не так, как F(X), и что в реальном мире практически все функции F нелинейны.
Разобраться нам поможет следующий пример. Рассмотрим выпуклую вверх платежную функцию F(X) = 1 – х2, где х – отклонение цены закрытия; таков ваш платеж за этот день, и если х не превышает единицу (допустим, единица — это среднеквадратическое отклонение цены закрытия), то вы в плюсе, а иначе несете убытки.
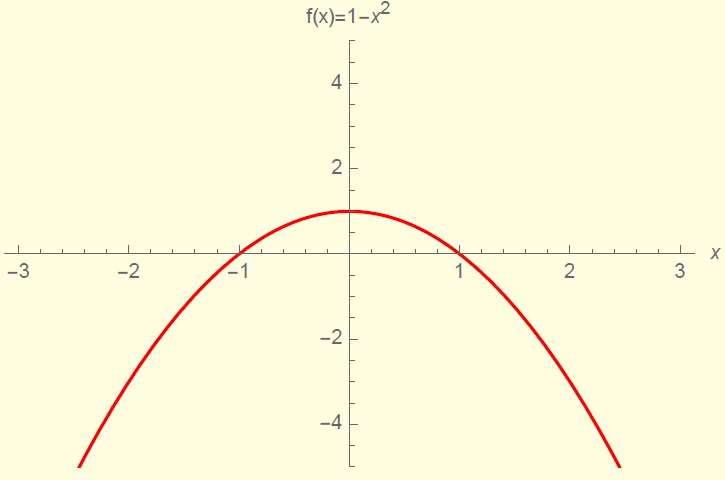
Рис. 3.31. Платежная функция
Теперь рассмотрим следующие две последовательности отклонения х в течение 7 дней (в тех же единицах, среднеквадратических отклонениях). Последовательность 1 (тонкохвостая): {1, 1, 1, 1, 1, 0, 0}. Среднее отклонение 0,71. Ваша чистая прибыль 2. Последовательность 2 (толстохвостая): {0, 0, 0, 0, 0, 0, 5}. Среднее отклонение 0,71 (то же самое). Ваша чистая прибыль = -18 – разорение.
В обоих примерах прогноз среднего 0,71 сбудется, но одна и та же стратегия в первом примере принесет прибыль, а во втором — убытки; все испортит неоднородность в волатильности — жирный хвост вероятностного распределения.
Вот почему в реальном мире из «плохих» прогнозистов получаются успешные трейдеры и ответственные руководители. Все профессионалы об этом знают, но литература по «прогностике», математически беспомощная и практически наивная, до сих пор не разобралась, в чем дело, после столетий кипучей активности.
Разорение и зависимость от пути
Напоследок поговорим о зависимости от пути и о вероятности по времени. Зависимость от пути означает следующее. Если я сначала поглажу рубашки, потом постираю, результат будет не такой, как если сначала постирать, а потом огладить.
Разберемся сначала, что такое вероятности для статистического ансамбля. Допустим, что мы — это 100 случайно выбранных человек и что мы отправились в казино. Если 28-й игрок разорился, это не помешало 29-му играть дальше. Значит, можно посчитать доход от похода в казино, сложив наши 100 результатов. Закон больших чисел позволяет нам повторить опыт 2–3 раза и точно измерить так называемое преимущество данного казино.
Проблема появится при попытке применить это ансамблевое свойство к 100 визитам одного человека. Прежний подход не сработает, потому что если он на 28-й день разорится, то на 29-й день уже не придет. По этой причине Крамеру пришлось сформулировать условие Крамера, за пределами которого страхование не работает; по этому условию недопустим риск разорения из-за одного потрясения. Аналогичным образом отдельный инвестор не может достигнуть доходности, равной среднему показателю фондового рынка, потому что ресурсы отдельного инвестора конечны.
Добиться дохода на фондовом рынке можно лишь при выполнении строгих условий. Вероятность по времени и вероятность по ансамблю — не одно и то же. Активному инвестору удается приблизиться к вероятности по ансамблю, только если этот инвестор использует политику распределения ресурсов.
Если мы решим кататься на мотоцикле с небольшим риском катастрофы, но много раз, мы заметно сократим ожидаемую продолжительность жизни. Измерить это можно так.
Принцип (Повторение воздействия). Фокусируйтесь на сокращении ожидаемого срока службы того модуля, который подвергается многократному воздействию с некоторой плотностью, или частотой.
Финансовые теоретики-бихевиористы пока что выводят свои суждения из статики, не динамики, и поэтому данную картину не видят. Они вырывают компромиссы из контекста и приходят к консенсусу, будто человеку свойственно иррационально преувеличивать хвостовые риски (и его надо подталкивать к более смелым действиям). Но катастрофическое событие является барьером. Смелые действия нельзя анализировать по отдельности: риски накапливаются. Если мы катаемся на мотоцикле, курим, водим винтовой самолет и вступаем в мафию, перечисленные риски складываются в весьма вероятную преждевременную гибель. Хвостовые риски — не то же, что риск потерять заменимый ресурс.
Психология принятия решений
Психологическая литература фокусируется на воздействии одного эпизода и опирается на узкое определение анализа «затраты — выгоды». Иногда анализ объявляет людей параноиками, преувеличивающими небольшие риски; авторам такого анализа не приходит в голову, что при малейшей терпимости к набиранию хвостовых рисков мы не выжили бы на протяжении миллионов лет.
Эргодичность в этом контексте означает перенос результатов анализа вероятностей по ансамблю на вероятности по времени. Если перенос невозможен, игнорируйте вероятность по ансамблю.
***
Резюмируя, отметим как первую задачу необходимость различать Медиокристан и Экстремистан, две области, которые практически не перекрываются. Если мы не научимся видеть разницу, наши попытки анализа будут бессмысленны. Во-вторых, если мы не будем отличать вероятность по времени (зависящую от пути) и по ансамблю (независимую от пути), наши попытки анализа будут бессмысленны.
[1] Теорема Гаусса – Маркова утверждает, что если корреляцию между двумя случайными величинами X и Y представлять линейной регрессией уt = а + bхt + εt, то оценка коэффициентов a и b по методу наименьших квадратов оптимальна. Посылки этой теоремы: (1) корреляция представима линейной зависимостью, (2) все наблюдения Xt известны, (3) ошибки не содержат систематической ошибки, Еε = 0, (4) дисперсия ошибок конечна и постоянна, (5) ошибки не коррелированы между собой, Cov(εi,εj) = 0 при всех i, j.