Объяснение парадокса Монти Холла

Я преподаю магистрам курс «Статистическое мышление» и, объясняя термин пространство исходов, в качестве примера рассказываю о парадоксе Монти Холла. Напомню условия задачи в её классическом виде. Вы участник шоу, и вам показывают три одинаковые двери. За одной – авто, за двумя другими – козы. Монти Холл, ведущий шоу, просит вас выбрать одну из дверей. Вы делаете это, но не открываете выбранную дверь. Монти, который знает, где находится авто, открывает одну из двух других дверей. Он выбирает свою дверь в соответствии со следующими правилами:

• Монти всегда открывает дверь, за которой скрывается коза.
• Монти никогда не открывает дверь, которую вы выбрали изначально.
• Если Монти может открыть более одной двери, не нарушив первые два правила, то он выбирает свою дверь случайным образом.

После того, как Монти откроет свою дверь, он предлагает вам остаться с первоначальным выбором или переключиться на другую неоткрытую дверь. Что нужно сделать, чтобы максимизировать свои шансы на выигрыш автомобиля? Обоснуйте свой ответ прежде чем читать далее.

Рис. 1. Классические правила: после вашего выбора Монти Холл открывает одну из двух оставшихся дверей, за которой скрывается коза

Скачать заметку в формате Word или pdf, примеры в формате Excel

Следует сказать, что магистры делятся на тех, кто понимают решение, и не понимают. Причем аргументы редко помогают изменить мнение тех, кто решение не понимает. И вот недавно натолкнулся на довольно любопытный обзор [8], сокращенный перевод которого вам и представляю. К аргументам автором я также добавил моделирование в Excel.

Во всей истории математики трудно найти задачу, которая вызывала бы такие страсти, как задача Монти Холла (ЗМХ). Её история восходит к 1959 году, когда Мартин Гарднер представил версию в журнале Scientific American [4, 5]. Когда в 1965 году статистик Фред Мозетеллер включил ее в антологию вероятностных задач [9], он заметил, что она привлекла гораздо больше внимания, чем любая другая задача. В современном формате игрового шоу проблема появилась в 1975 году в выпуске академического журнала The American Statistician [14]. Математик Стив Селвин представил её как интересное упражнение по условной вероятности. Несмотря на то, что он привел верное решение, на него обрушился шквал нападок в последовавших письмах в редакцию [15].

Очередной виток напряженности возник после публикации Мэрилин вос Савант в журнале Parade. За этим последовало несколько раундов гневной переписки, в которой читатели оспаривали решение вос Савант. Позже претендентам пришлось съесть ворону, когда симуляция Монте-Карло показала, что вос Савант была права, но не раньше, чем ссора попала на первую полосу «Нью-Йорк Таймс» [18]. Вся эта история изложена в [13].

Лучше всего ситуацию охарактеризовал ученый-когнитивист Массимо Пальмателли-Пальмарини, который писал: «… Ни одна другая статистическая головоломка не может быть так близка к тому, чтобы постоянно дурачить всех людей… Этот феномен особенно интересен именно своей спецификой, воспроизводимостью и невосприимчивостью к высшему образованию» [10].

К чему вся эта путаница?

Беда в том, что большинство людей рассуждают так: «Как только Монти открывает свою дверь, в игре остаются две двери. Поскольку они с равной вероятностью будут правильными, не имеет значения, переключаетесь вы или нет». Мы будем называть этот аргумент 50 на 50.

Эта интуиция подкрепляется хорошо известной человеческой склонностью. Отрицательное последствие, вызванное бездействием, причиняет меньший вред, чем то же самое негативное последствие, вызванное каким-либо действием. В контексте ЗМХ люди чувствуют себя хуже, когда они изменяют выбор и проигрывают, чем после проигрыша, связанного с сохранением первоначального выбора.

В журналах по психологии и когнитивным наукам довольно много публикаций, объясняющих трудности, с которыми сталкиваются люди при решении ЗМХ. Бернс и Вит [3] суммировали результаты, написав:

Ранее сообщалось о 13 исследованиях с использованием стандартных версий ЗМХ, и частота переключений варьировалась от 9% до 23% со средним значением 14,5%.

Гилович, Медвек и Чен [6] изучали реакцию людей на проигрыш при сохранении выбора и переключении. Они использовали коробки вместо дверей и создали экспериментальную ситуацию, в которой игроки проигрывали независимо от того, решили они переключиться или нет. К каким выводам пришли исследователи?

Поскольку действие имеет тенденцию отклоняться от нормы в большей степени, чем бездействие, человек, скорее всего, будет чувствовать себя более ответственным за неудачный поступок. Таким образом, испытуемые, которые меняли коробки в нашем эксперименте, с большей вероятностью испытывали чувство «Я навлек это на себя» или «Этого не должно было случиться», чем испытуемые, которые решили оставить свою первоначальную коробку.

Казалось бы, защитники сохранения выбора могут указать, как на правдоподобный математический аргумент, так и на некоторые тонкости человеческой психологии. Однако…

Сосредоточьтесь на Монти, а не на дверях

Существует множество методов решения ЗМХ. Построение древовидной диаграммы (рис. 2) показывает, что переключение выигрывает с вероятностью 2/3 , а сохранение выбора – с вероятностью 1/3. Следовательно, переключаясь, вы удваиваете шансы на победу.

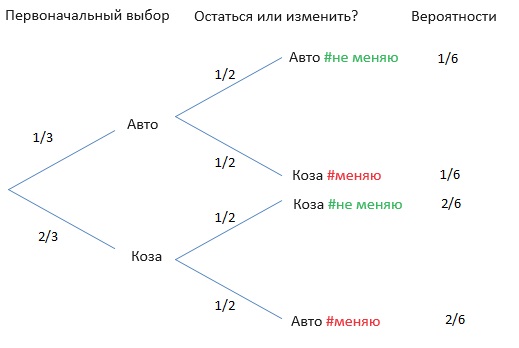
Рис. 2. Дерево решений ЗМХ. Стратегия #не меняю с вероятностью 1/6 даёт авто, и 2/6 – козу. Стратегия #меняю, наоборот: 2/6 – за авто и 1/6 – за козу

Использование метода Монте-Карло – второй путь для получения правильного ответа. Сценарий Монти Холла легко смоделировать в Excel.

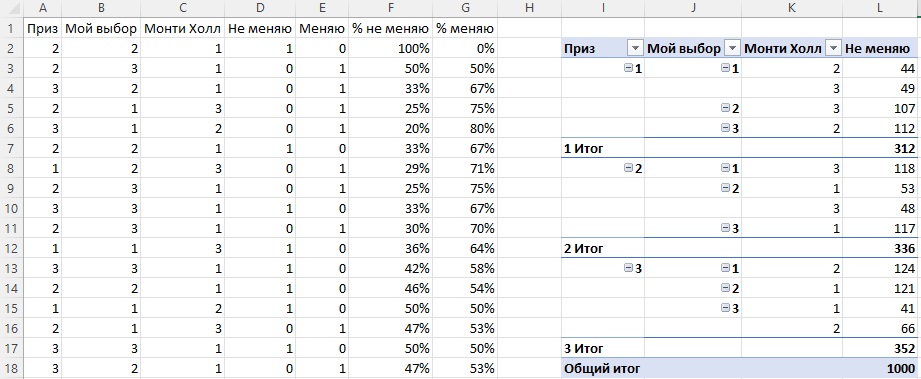
Рис. 3. Модель в Excel (слева) и проверка её релевантности сводной таблицей (справа)

В столбце А случайным образом из чисел 1, 2, 3 тысячу раз выбираю номер двери, за которой прячется приз. Формула в Excel =СЛМАССИВ(1000;;1;3;ИСТИНА). В столбце В аналогичной формулой задаю номер дверь первоначально выбранной игроком. В столбце С наиболее сложный фрагмент модели с использованием формулы в ячейке С2:

Проверяю условие (строка 2), если дверь с призом и первоначальный выбор игрока не совпадают, то у Монти единственная возможность открыть третью дверь (3). Если приз и выбор игрока совпадают (4), и игрок выбрал дверь 1 (5), то Монти случайным образом выбирает из дверей 2 и 3 (6). Если приз и выбор игрока совпадают, и игрок выбрал дверь 3 (8), то Монти случайным образом выбирает из дверей 1 и 2 (9). Если приз и выбор игрока совпадают, и игрок выбрал дверь 2, то с вероятностью 50 на 50 (11) Монти выбирает из дверей 1 (12) и 3 (13).

В столбце D формулой =ЕСЛИ(A2=B2;1;0) присуждаю выигрыш (значение 1) если дверь с призом и первоначальный выбор игрока совпадают и поражение (значение 0), если не совпадают. В столбце Е формулой =ЕСЛИ(A2=B2;0;1), наоборот присуждаю выигрыш за удачную смену двери и поражение – за изменение, приведшее к неудаче.

В столбце F формулой =СУММ($D$2:D2)/СЧЁТЗ($D$2:D2) нахожу скользящую (кумулятивную) долю выигрышей при сохранении первоначального выбора. В столбце G формулой =СУММ($E$2:E2)/СЧЁТЗ($E$2:E2) нахожу скользящую долю выигрышей при изменении первоначального выбора.

Справа от модели (см. рис. 3) с помощью сводной таблицы проверяю адекватность модели. С моделью можно поиграть в приложенном Excel-файле. Поскольку использованы волатильные функции после нажатия F9 случайные числа пересчитываются, и данные в модели и на графике моментально изменяются. Сводная таблица требует ручного обновления.

Спустя всего несколько раундов игры большое преимущество от переключения, становится очевидным:

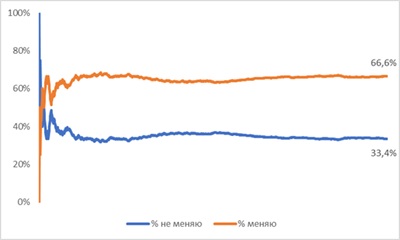
Рис. 4. Изменение выбора асимптотически стремится к 66,7%, а сохранение выбора – к 33,3%; по оси абсцисс итерации

Такие методы, однако, мало что дают для прояснения того, почему аргумент 50 на 50 неверен. Практические результаты, полученные в результате моделирования, могут показать вам, что с вашей интуицией что-то не так, но они не сделают правильный ответ естественным. Проблема заключается в том, что людям трудно понять, что важно, а что нет в рассуждениях об условной вероятности.

Мантра, вынесенная в заголовок этого раздела, имеет большое значение для того, чтобы указать правильное направление размышлений. Когда Монти открывает дверь Х, вы возможно думаете: «Я узнал, что за дверью Х скрывается коза, но я не узнал ничего существенного о двух других дверях». Это то, что мы имеем в виду, когда говорим сосредоточенность на дверях. Правильный подход заключается в том, чтобы сосредоточиться на Монти, в частности, на том, как именно он выбирает свою дверь, чтобы открыть её. Мы должны думать: «Монти, который принимает решения в соответствии со строгими правилами, решил открыть дверь Х. Почему именно эту дверь, а не иную?»

Предположим, что игрок выбрал первую дверь, а Монти открыл вторую. Согласно правилам, разыгрался один из сценариев:

• Авто – за первой дверью. Монти наугад выбрал вторую дверь из оставшихся.
• Авто – за третьей дверью, и у Монти не было выбора.

Второй из этих сценариев более вероятен, чем первый. Поскольку авто находится за первой дверью в одной трети случаев, а Монти затем открывает вторую дверь в половине этих случаев, вероятность сценария 1/3*1/2=1/6. Второй сценарий происходит всякий раз, когда машина находится за третьей дверью. Это происходит в трети случаев. Второй сценарий в два раза более вероятен, чем первый.

Вы должны думать: «Я только что стал свидетелем события, которое в два раза чаще происходит, когда автомобиль находится за третьей дверью, чем когда автомобиль находится за первой дверью. Следовательно, у меня больше шансов выиграть авто, переключившись».

Общий принцип – все, что влияет на процесс принятия решений Монти, имеет отношение к обновлению ваших вероятностей после того, как Монти откроет свою дверь. Чтобы еще больше прояснить этот момент, рассмотрим измененный вариант ЗМХ.

Версия 2 (Монти с большим номером)

Как и прежде, у вас три одинаковые двери, скрывающие одну машину и двух коз. Вы выбираете дверь, которая остается неоткрытой. Монти открывает дверь, в которой, как он знает, прячется коза. На этот раз, однако, мы оговариваем, что Монти всегда открывает дверь с самым большим номером (имея в виду, что Монти никогда не откроет дверь, выбранную игроком). Получит ли игрок какое-либо преимущество, поменяв дверь?

Для определенности предположим, что игрок изначально выбрал первую дверь.

Каждый раз, когда за дверью, выбранной игроком, скрывается коза, у Монти нет выбора, какую дверь открыть. Он не может открыть первую дверь (так как игрок выбрал эту дверь), и он не может открыть дверь, которая скрывает авто. Таким образом, для него остается только одна дверь.

Интересен случай, когда за первой дверью скрывается авто. В отличие от классического варианта, теперь Монти открывает третью дверь, когда может. Из этого следует, что если мы видим, что он открывает вторую дверь, мы точно знаем, что машина находится за третьей дверью.

А если Монти откроет третью дверь? Поскольку Монти наверняка откроет третью дверь всякий раз, когда машина находится за первой или второй дверью, у нас теперь нет оснований для выбора между ними. В данном случае это действительно решение 50 на 50.

Воспринимайте это как предостережение – любое решение ЗМХ, не уделяющее внимания процедуре отбора Монти, является неполным.

Монти встречает Байеса

Итак, вероятность того, что дверь X скрывает машину, учитывая, что Монти показал нам козу за дверью Y, зависит от рассмотрения процедуры выбора Монти. Точнее, это зависит от вероятности того, что Монти откроет дверь Y, предполагая, что дверь X скрывает машину. Точный способ связи этих вероятностей задается теоремой Байеса.

Мы обозначаем через C_i событие, когда машина находится за дверью i, а через M_j событие,  когда Монти открывает дверь j, чтобы показать козу. Также предположим, что игрок сначала выбирает первую дверь, а Монти открывает вторую. Вероятность нахождения авто за дверью 1, если Монти открыл дверь 2 – P(C₁│M₂) по теореме Байеса равна:

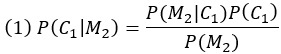
Разложение знаменателя по закону полной вероятности приводит к

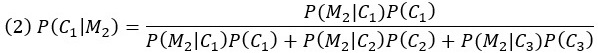
В классической версии ЗMХ P(M₂|C₂) = 0, так как дано, что Монти никогда не откроет дверь, скрывающую авто. Кроме того, априорные вероятности равны: P(C₁) = P(C₂) = P(C₃) =  1/3. Подставим

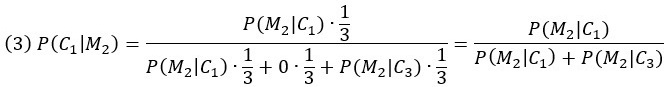
Заметим, что когда игрок выбирает первую дверь, а машина находится за третьей, Монти обязательно откроет вторую, т. е. P(M₂|C₃) = 1. В классической версии P(M₂|C₁) = 1/2,  так как Монти выбирает случайным образом, когда машина находится за дверью, изначально выбранной игроком. В версии 2 (с большим номером) P(M₂|C₁) = 0, так как Монти обязан открыть третью дверь. Подставляя в формулу Байеса, мы получаем для классического Монти:

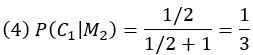
…для версии 2:

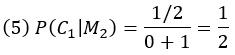
Именно такие ответы мы получили в предыдущем разделе.

Ссылки

[3] Bruce Burns, Mareike Wieth, “The Collider Principle in Causal Reasoning: Why the Monty Hall Problem is so Hard,” Journal of Experimental Psychology, General, Vol. 103, No. 3, 2004, pp. 436-449.

[4] Martin Gardner, “Problems Involving Questions of Probability and Ambiguity,” Scientific American, Vol. 201, No. 4, April 1959, pp. 174-182.

[5] Martin Gardner, “How Three Modern Mathematicians Disproved A Celebrated Conjecture of Leonhard Euler,” Scientific American, Vol 201, No. 5, May 1959, pp. 188.

[6] T. Gilovich, V. H. Medvec, S. Chen, “Commission, Omission, and Dis-sonance Reduction: Coping with Regret in the “Monty Hall Problem,” Personality and Social Psychology Bulletin, Vol. 21, No. 2, February 1995, pp. 182-190.

[8] Stephen Lucas, Jason Rosenhouse, Andrew Schepler. “The Monty Hall Problem”, Mathematics Magazine, Vol. 82, No. 5 (December 2009), pp. 332–342.

[9] Fred Mosteller, Fifty Challenging Problems in Probability, With Solutions, Addison-Wesley Inc., Reading, 1965.

[10] Massimo Piattelli-Palmarini, “Probability Blindness, Neither Rational Nor Capricious”, Bostonia, March/April 1991, pp. 28-35.

[13] Marilyn vos Savant, The Power of Logical Thinking, St. Martin’s Press, New York, 1996.

[14] Steve Selvin, “A Problem in Probability,” (Letter to the Editor), The American Statistician, Vol. 29, No. 1, 1975, pp. 67.

[15] Steve Selvin, “On the Monty Hall Problem,” (Letter to the Editor), The American Statistician, Vol. 29, No. 3, 1975, pp. 134.

[18] John Tierney, “Behind Monty Hall’s Doors, Puzzle, Debate and Answer?” The New York Times, July 21, 1991, pp. 1A.