Недавно прочитал книгу Майкла Херцога с соавторами Статистика и планирование эксперимента для непосвященных. В ней я в очередной раз встретился со статистической мощностью. До сих пор я относился к этой статистике несколько академически. Что называется, не чувствовал её на кончиках пальцев. Некоторые разделы книги Херцога меня заинтересовали, я построил пару моделей в Excel и осознал, что статистическая мощность – это вероятность получить в эксперименте статистически значимые результаты. Кроме того, я нашел формулу расчета статистической мощности в Excel. Свои выводы я представил в заметке Статистическая мощность эксперимента в Excel. В книге Майкл Херцог также упоминает о калькуляторе статистической мощности G*Power. Предлагаю вам краткий обзор программы G*Power основанный на переводе статьи Susanne Mayr, Edgar Erdfelder, Axel Buchner, Franz Faul. A short tutorial of GPower, опубликованной в журнале Tutorials in Quantitative Methods for Psychology. – 2007, Vol. 3(2), p. 51–59.
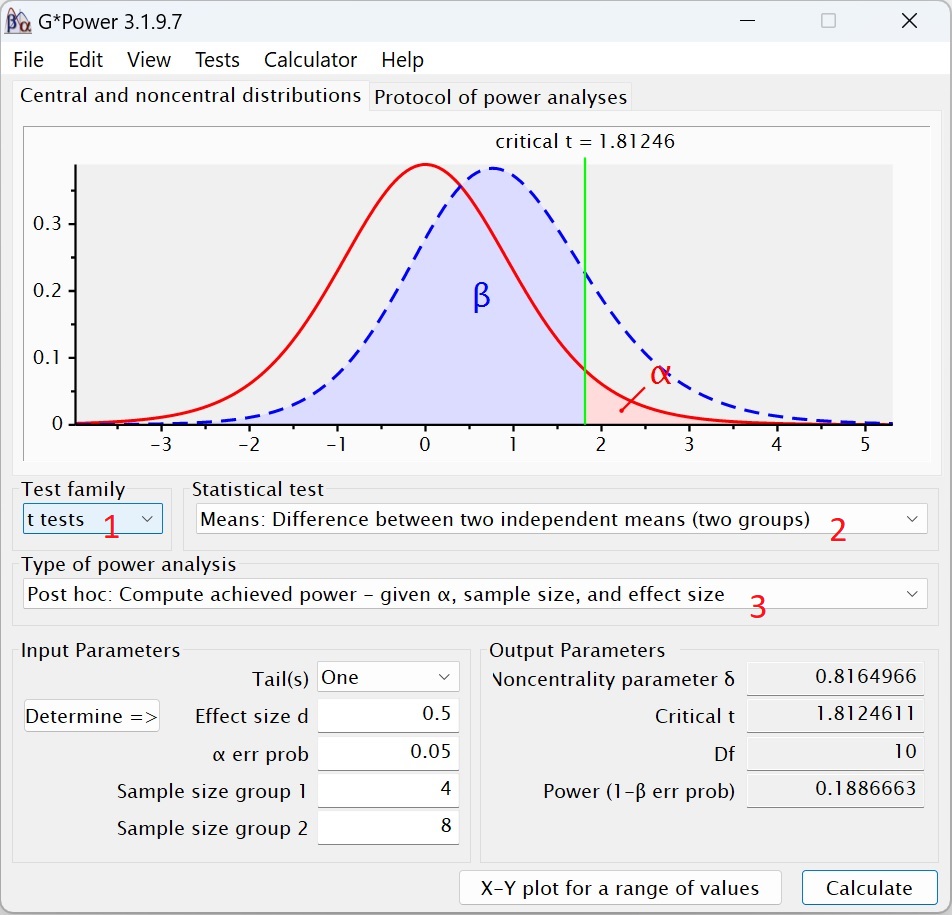
Рис. 1. Анализ статистической мощности в GPower: апостериорный t-тест для независимых выборок
Скачать заметку в формате Word или pdf
Целью статьи является презентация статистического анализа мощности в поведенческих науках на основе использования бесплатной программы GPower. ПО доступно для Mac OS и Windows.[1] Представлены примеры психологических исследований, иллюстрирующие различные возможности GPower. В частности, априорный, апостериорный и компромиссный анализ мощности для t-, F- и χ2— тестов. Для всех примеров описаны основные статистические концепции и реализация в GPower.
В поведенческих науках мы обычно применяем статистические тесты, а вот анализ статистической мощности выполняем не всегда. Однако, без контроля статистической мощности трудно интерпретировать незначимые результаты. Статистические тесты могут давать незначимые результаты, потому что (а) нулевая гипотеза H0 выполняется (правильный пропуск, Correct Rejection) или (б) альтернативная гипотеза H1 выполняется, но тест не был достаточно мощным для обнаружения отклонений от H0 (ошибочный пропуск). Не существует разумного способа выбора между толкованиями (а) и (б) когда мощность испытания неизвестна. Из-за пренебрежения статистическим анализом мощности незначимые результаты публикуются очень редко. Таким образом, публикация результатов исследований смещена в пользу гипотез H1.
Отсутствие анализа мощности часто оправдывают его сложностью. Представленное ПО позволит преодолеть эту сложность.
Виды анализа мощности
Выделяют три вида анализа статистической мощности. Априорный проводят до исследования. Он используется для определения размера выборки N, который позволит с заданным уровнем ошибки I-го рода α, желаемой статистической мощностью (1 – β) выявить эффект размера d, т.е. разницу между H0 и H1.
Апостериорный анализ проводится после исследования, чтобы при заданных размере выборки N и размере эффекта d оценить статистическую мощность (1 – β), или вероятность ошибки II-го рода β. Апостериорный анализ слабее априорного, поскольку в нем контролируется только α. Как β, так и ее дополнение (1 – β) только оцениваются. Апостериорный анализ можно охарактеризовать как инструмент, обеспечивающий критическую оценку (часто удивительно большой) вероятности ошибки β, связанной с ложным решением в пользу H0.
Компромиссный анализ мощности, обеспечивает прагматическое решение часто встречающейся проблемы, заключающейся в том, что идеальный размер выборки N, рассчитанный с помощью априорного анализа, превышает доступные ресурсы. Т.е., ищут разумный компромисс между малым N и приемлемой мощностью (1 – β). Для этого оценивают коэффициент q = β/α. Основываясь на N, q и размере эффекта d, результат анализа компромиссной мощности выдает α и β и связанное с ними критическое значение тестовой статистики. Другими словами, анализ компромиссной мощности контролирует отношение вероятности ошибок q. И α, и β оцениваются с учетом фиксированного отношения вероятностей ошибок q.
Анализ статистической мощности для t-тестов
Независимые выборки
Часто цитируемое исследование Уоррингтона и Вайскранца (Warrington, E. K., & Weiskrantz, L. (1970). Amnesic syndrome: Consolidation or retrieval? Nature, 228, 628–630, эксперимент 2) сравнивало память пациентов с амнезией и контрольной группы. В тесте на завершение слова пациенты с амнезией заполнили меньше словесных основ словами, которые они видели раньше. Но различие между средними значениями в группах было незначительным: 14,5 против 16. Выборка включала только четырех пациентов с амнезией и 8 – из контрольной группы. Статистическая мощность t-критерия для независимых выборок должна была быть довольно маленькой. Кроме того, неодинаковые размеры выборки в двух группах, как правило, снижают статистическую мощность.
Разберем настройку GPower (см. рис. 1). Выбран t-тест (цифра 1 на рис. 1) для разницы двух независимых выборок (2) и апостериорный анализ статистической мощности (3). Слева заданы параметры: вид теста – односторонний, ожидаемый размер эффекта d, ошибка I-го рода α, размер первой и второй выборки. Справа представлены итоги расчетов: нецентральный параметр δ, t-критическое, число степеней свободы df, мощность (1 – β).
Нецентральный параметр δ – это значение на оси абсцисс, соответствующее максимуму распределения альтернативной гипотезы Н1 (пунктирная синяя колоколообразная кривая на рис. 1).
![]()
где n1 и n2 – размеры выборок двух групп (с амнезией и контрольной), N = n1 + n2, размер эффекта d = (μ1 + μ2) / σ. Размер эффекта также называют d Коэна. μ1 и μ2 – матожидания генеральных совокупностей, из которых извлечены две выборки, σ – общее стандартное отклонение двух популяций. Нулевая гипотеза H0 одновыборочного t-теста формулируется как μ2 – μ1 ≤ 0, альтернативная гипотеза H1 предполагает μ2 – μ1 > 0. Для заданного совокупного размера выборок и заданного d уравнение (1) показывает, что чем больше неравномерность в размере групп, тем меньше δ, и, следовательно, тем меньше статистическая мощность.
Но насколько велика статистическая мощность для результатов теста на завершение слова? Предположим, что для всей популяции матожидания равнялись 14,5 для пациентов с амнезией и 16 для контрольной группы. К сожалению, о величине стандартного отклонения или эмпирическом t-значении в статье не сообщалось. Предположим, что σ = 3. Поскольку альтернативная гипотеза является направленной в GPower выбираем односторонний тест. d = (16–14,5)/3 = 0,5. Эффект такого размера Коэн считал средним. Какова была вероятность найти этот эффект при уровне значимости α = 0,05? Рассчитанная величина статистической мощности (1 – β) = 0,1887 разочаровывает.
Вывод. Едва ли можно было обнаружить дефицит амнезии среднего размера в задаче Уоррингтона и Вайскранца.
Мы можем использовать априорный анализ, чтобы определить размер выборок при заданном размере эффекта d = 0,5, позволяющий найти эту разницу со статистической мощностью (1 – β) = 0,9. Потребуются выборки по 70 человек.
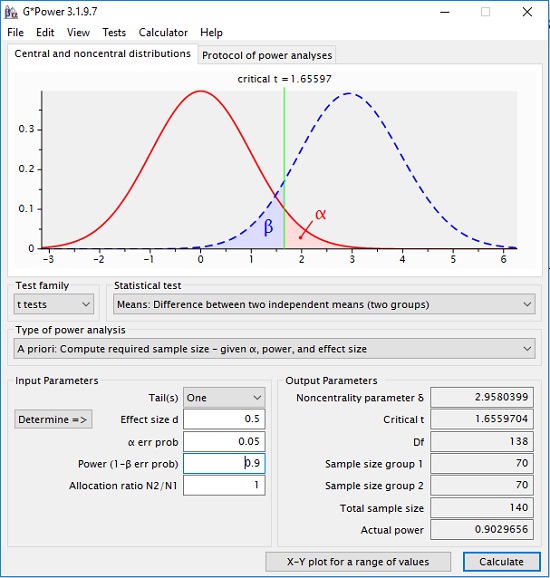
Рис. 2. Априорный анализ статистической мощности
В качестве альтернативы, если мы хотим обнаружить эффект размера d = 0,5 с n1 = 4, n2 = 8 и одинаково большими вероятностями ошибок α и β (q = 1), можно выбрать компромиссный анализ мощности. GPower возвращает α = β = 0,3422. В сложившихся обстоятельствах выбор этого уровня значимости является наилучшим возможным решением. Тем не менее, этот статистический тест вряд ли лучше, чем подбрасывание монеты, чтобы решить, принять или отклонить H0.
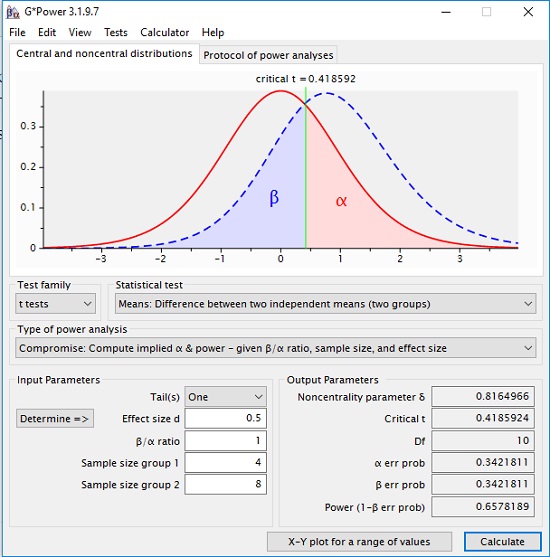
Рис. 3. Компромиссный анализ статистической мощности
Можно выбрать q > 1, если ошибка II-го рода представляется менее серьёзной, чем ошибка I-го рода.
t-тест для парных выборок
Вслед за работой Гезелла и Томпсона (Gesell, A., Thompson, H. Learning and growth in identical infant twins) был проведен ряд экспериментов с монозиготными парами близнецов, в ходе которых один случайно выбранный близнец тренировал определенные двигательные навыки, в то время как другой не получал никакой программы обучения. Это позволило провести контролируемое исследование того, развиваются ли определенные способности (например, обучение ходьбе, контроль мочевого пузыря) в процессе созревания или влияние окружающей среды может способствовать или ухудшать это развитие.
Представьте себе, что мы хотим повторить такое близнецовое исследование, которое должно быть проанализировано с помощью парных образцов t-критерия. Предположим далее, что имеется только пул из 20 пар близнецов. Каковы разумные вероятности ошибок, которые мы должны принять для нашего статистического теста?
X и Y обозначают возраст, в котором тренированный и нетренированный близнец овладеют особой двигательной способностью. H0 парной выборки одностороннего t-критерия характеризуется как μx–y = μx – μy ≤ 0, где μx–y обозначает среднее значение возрастных различий каждой пары близнецов. Величина эффекта dz определяется как:
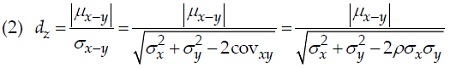
где σx–y – стандартное отклонение разностей (X – Y), covxy – ковариация, ρ – положительная корреляция между значениями X и Y в популяции, если H1 верна. При прочих равных условиях, чем больше корреляция ρ, тем меньше знаменатель и тем больше индекс величины эффекта dz. Если H1 истинно, то распределение тестовой статистики является нецентральным t-распределением df = N – 1 (N – количество пар-близнецов, т.е. пар измерения) и параметром нецентральности
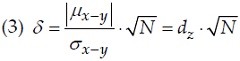
Предположим, что в среднем разница в развитии конкретного двигательного навыка составляет 2 месяца, а стандартное отклонение разницы в возрасте может составлять до 4 месяцев. Из уравнения (2) величина эффекта, которая должна быть обнаружена в этом исследовании, равна dz = 2/4 = 0,5. Поскольку N и dz заданы, нам нужен компромиссный анализ в GPower (рис. 4). Данные близнецов зависят друг от друга. Выберем вариант Difference between two dependent means (matched pairs), Разница между двумя зависимыми средними значениями (подобранными парами). Для этого варианта df равно не N – 2, как для независимых выборок. Здесь df = N – 1. Гипотеза снова направлена – мы хотим знать, превосходят ли обученные близнецы необученных. Напомню, для независимых выборок параметр нецентральности вычисляется по формуле (1). Если размеры двух выборок равны, записать можно упростить:
![]()
Для парных выборок параметр нецентральности
![]()
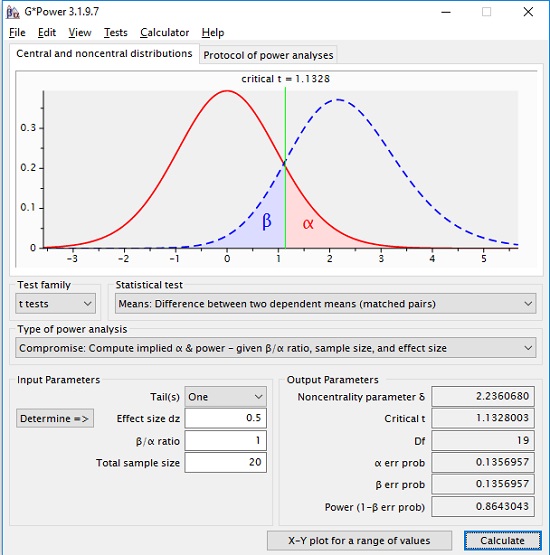
Рис. 4. Компромиссный анализ статистической мощности t-теста для парных выборок
Выберем q = 1. GPower возвращает параметр нецентральности δ = 2,2361 и рекомендует выбрать α = β = 0,1357. Статистическая мощность (1 – β) = 0,8643. Для того, чтобы отвергнуть H0 (гипотезу об отсутствии различий между близнецами) и принять H1, эмпирическое t-значение должно превышать критическое t(19) = 1,1328. Этот результат лучше, чем в предыдущем примере. Тем не менее, существует большая вероятность, как ошибки I-го рода, так и ошибки II-го рода.
Чтобы уменьшить вероятность ошибки, необходимо увеличить размер выборки. До какой степени нам придется увеличивать размер выборки, можно определить с помощью априорного анализа. Если наша цель α = 0,05 и β = 0,95, нужно исследовать 45 пар близнецов:
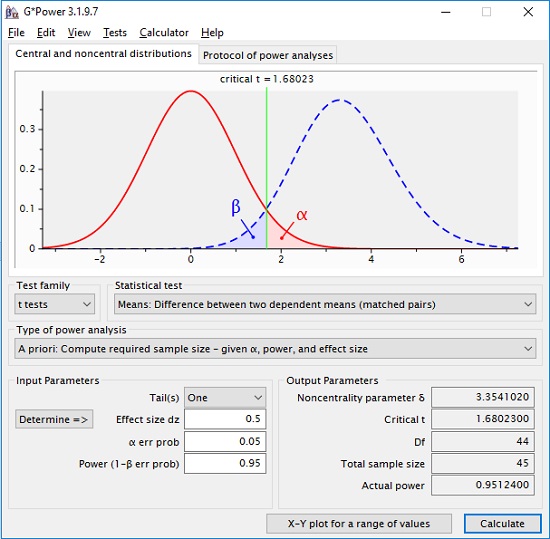
Рис. 5. Априорный анализ статистической мощности t-теста для парных выборок
t-критерий корреляций
Берри и Бродбент (Berry, D. C., Broadbent, D. E. On the relationship between task performance and associated verbalizable knowledge) исследовали связь между выполнением задач по управлению компьютерной симуляцией и вербализуемыми знаниями о симулируемой системе. В эксперименте 1 была обнаружена отрицательная корреляция (в диапазоне от -0,25 до -0,30) между этими двумя переменными. Чем лучше участники управляли симуляцией, тем хуже они могли давать информацию о симулируемой системе
Однако эта отрицательная корреляция не была статистически значимой. Авторы объяснили отсутствие значимости малой выборкой (N = 12). Но насколько велика была вероятность найти корреляцию определенного размера в этом исследовании? Взгляните на определение параметра нецентральности δ t-теста для корреляции между двумя переменными:
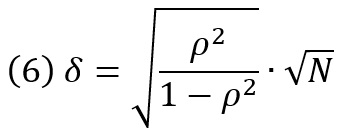
где ρ – корреляция генеральной совокупности, связанная с H1, а N – размер выборки, то есть количество пар измерения. Согласно Коэну, корреляции ρ = 0,30 определяются как эффекты среднего размера. Каковы шансы найти эффект этого размера в эксперименте, подобном тому, который описан Берри и Бродбентом?
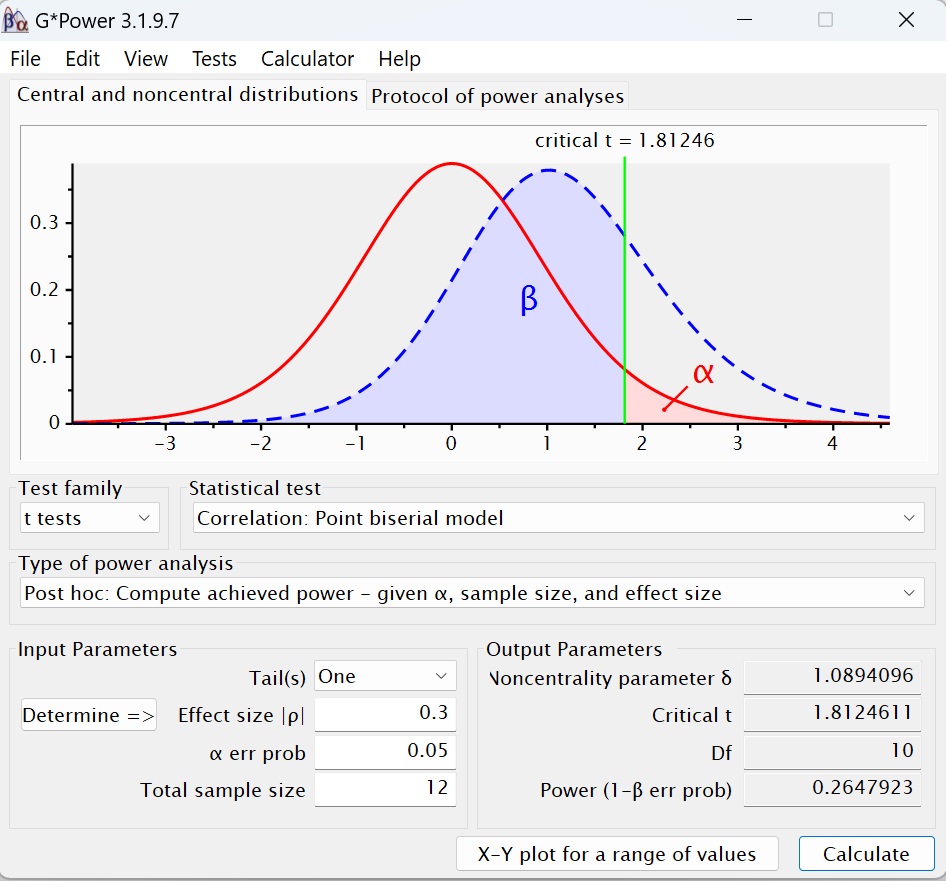
Рис. 6. Апостериорный анализ статистической мощности t-теста для корреляции
Настроим GPower: t-тест; Correlation: Point biserial model, Корреляция: точечная бисериальная модель, апостериорный анализ статистической мощности. Однонаправленный тест, потому что мы хотим протестировать H0: ρ ≥ 0 по сравнению с H1: ρ < 0. Размер корреляции ρ = 0,3, α = 0,05, N = 12.
Результаты анализа: параметр нецентральность δ = 1,0894, t-критическое t(10) = 1,8125. Статистическая мощность (1 – β) = 0,2648. То, что Берри и Бродбент не нашли значимой корреляции, кажется очень правдоподобным: их исследованию не хватало статистической мощности. Но насколько большой должна быть выборка? Проведем априорный анализ для (1 – β) = 0,95. Требуемый размер выборки равен N = 111.
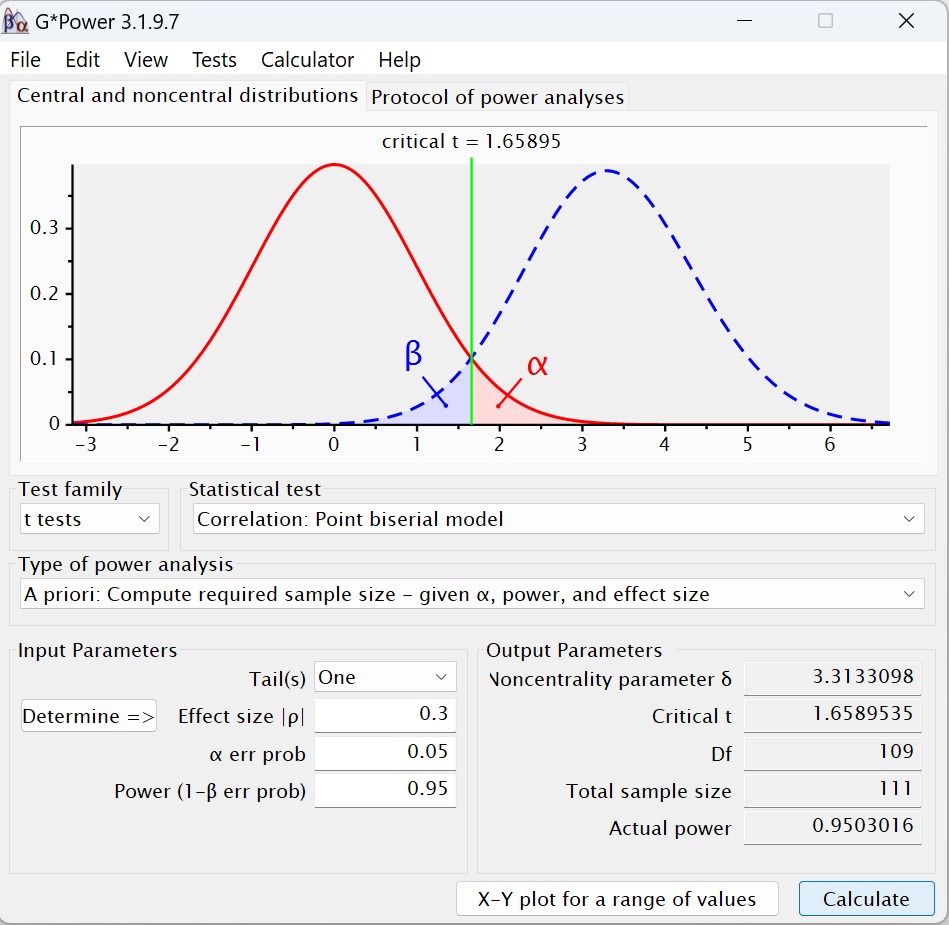
Рис. 7. Априорный анализ статистической мощности t-теста для корреляции
Анализ мощности для F-тестов
Мы ограничимся описанием анализа мощности для дисперсии для фиксированных эффектов. Индекс релевантности размера эффекта обозначается f или f2. Связь между f2 и параметром нецентральности λ нецентрального F-распределения определяется формулой:
![]()
где n – количество испытуемых в каждой из k групп. Индекс размера эффекта f определяется как:
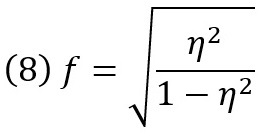
где η2 – величина общей дисперсии генеральной совокупности, объясняемая групповыми различиями, указанными в Н1. В случае неравных размеров выборки групп nj, индекс размера эффекта f равен
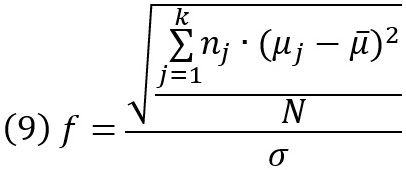
где nj – количество испытуемых, μj – среднее значение в популяции j, μ̅ – средневзвешенное значение k популяций, N – размер всех выборок, σ – стандартное отклонение популяции в каждой группе.
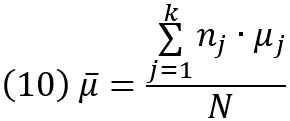
Однофакторный анализ
Шмитт, Хозер и Швенкмезгер (Schmitt M., Hoser K., Schwenkmezger P. Schadensverantwortlichkeit und Ärger) исследовали, зависит ли гнев, выраженный в ответ на ущерб, причиненный другим лицом, от степени ответственности виновных за этот ущерб. Степенью ответственности манипулировали в шести условиях. Предположим, что мы хотим повторить исследование Шмитта и др. H0 подразумевает, что шесть групп не различаются по степени выраженного гнева. Мы будем основывать оценку размера популяционного эффекта для нашего вымышленного примера на эмпирическом эффекте, который был обнаружен в рассматриваемом исследовании.
GPower позволяет рассчитать этот эффект. Выберите F-тест. Далее ANOVA; Fixed effects, omnibus, one-way, априорный тест.
Прим. Багузина. Этот комментарий подготовлен с помощью Chat GPT. ANOVA (ANalysis Of VAriance, дисперсионный анализ) – статистический метод, позволяющий определить, есть ли статистически значимые различия между средними значениями двух или более групп данных. Fixed effects, фиксированные эффекты – означает, что группы выбраны заранее. Например, мы хотим сравнить влияние трех лекарств. Случайные эффекты, с другой стороны, формируются исследователем на основе случайной выборки участников эксперимента. Например, если мы исследуем эффект групповой терапии на уменьшение депрессии, то мы можем случайным образом назначать участников в группы терапии и контрольную. Omnibus (от лат. omnibus — всем, каждому) указывает на то, что тестируются все группы одновременно, а не попарно или как-то еще. Н0 предполагает, что все средние одинаковые, а Н1 – что хотя бы одно среднее отличается. One—way означает, что дисперсионный анализ является однофакторным. Т.е., исследуется влияние лишь одного независимого фактора на зависимую переменную. Например, мы исследуем влияние разных методов обучения на успеваемость учеников. Фактор – метод обучения, а группы – ученики, которые проходили обучение с использованием разных методов. Таким образом, ANOVA Fixed effects, omnibus, one—way означает Однофакторный дисперсионный анализ фиксированных групп с одновременным оцениванием средних всех групп.
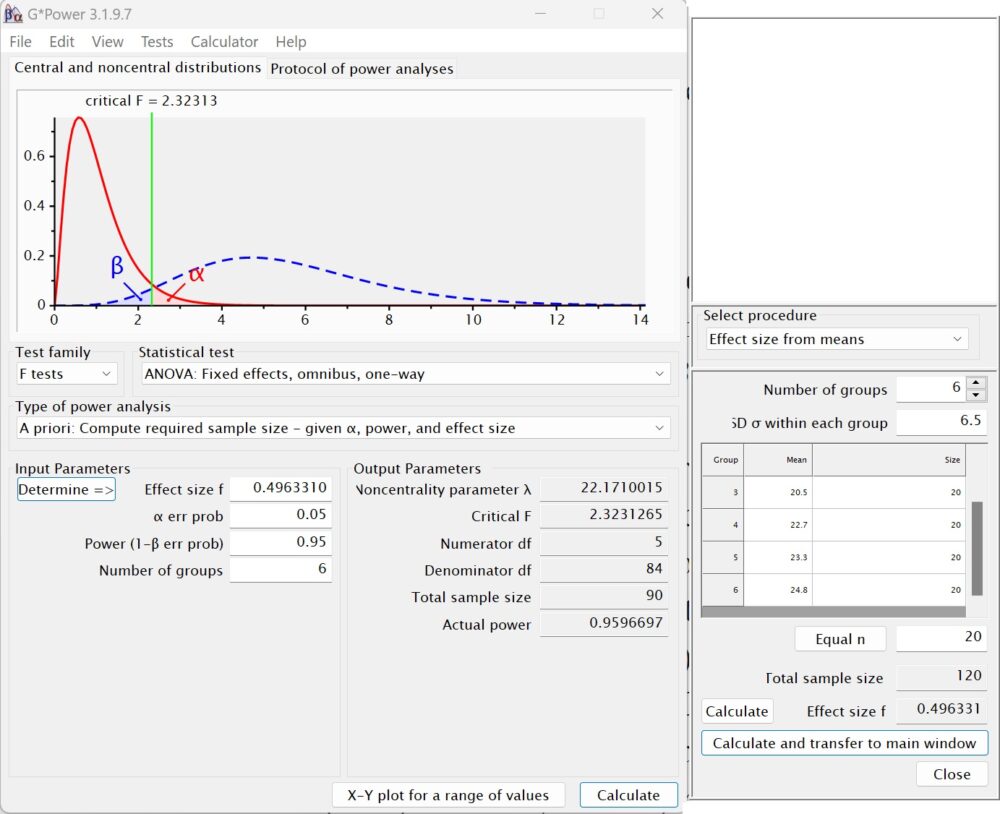
Рис. 8. Априорный анализ статистической мощности однофакторного F-теста
Установите ошибку I-го рода α = 0,05, желательную статистическую мощность (1 – β) = 0,95, количество групп = 6. Далее кликните на кнопку Determine. Откроется окно справа. Ведите средние значения из статьи Шмитта: 15,3, 18,3, 20,5, 22,7, 23,3 и 24,8. Рядом с кнопкой Equal n введите размер выборок (20), и нажмите кнопку Equal n. Введите стандартное отклонение σ = 6,5 (Шмит сообщил мне это значение в приватной беседе). Нажмите Calculate. Получим f = 0,4963. Нажмите Calculate and transfer to main window, чтобы перенести расчет в главное окно. Нажмите в нем кнопку Calculate. GPower вернет параметр нецентральности λ = 22,1682, F-критическое F(5, 84) = 2,3231. Для заданной мощности = 0,95 количество участников даже можно сократить до N = 90, то есть по 15 в группе.
Многофакторный анализ
Коэл в своей статье (Koele, P. Calculatingpower in analysis of variance) приводит статистический анализ мощности для сложных планов. Предположим, мы проводим эксперимент A × B с фиксированными эффектами. Фактор А включает kA = 3 уровня, фактор B – kB = 4 уровня. Какова статистическая мощность для проверки двух основных эффектов, а также для проверки взаимодействия эффектов? Процедура аналогична описанной выше однофакторной процедуре. Однако число степеней свободы уменьшается: df = N – kA × kB. Следуя примеру Коэла, мы выбираем апостериорный анализ, F-тест, ANOVA: Fixed effects, special, main effects and interactions.
Устанавливаем ошибку I-го рода α = 0,05. Выбираем размер эффекта f2 = 0,05; соответственно в GPower указываем f = 0,2236. Из статьи Коэла узнаем, что в каждой из 12 ячеек плана есть 10 наблюдений. Таким образом, общий размер выборки N = 120. Количество групп = 12. Чтобы вычислить статистическую мощность фактора A, укажем число степеней свободы для этого фактора df = kA – 1 = 2. GPower возвращает параметр нецентральности λ = 5,9996, критическое F-значение F(2, 108) = 3,0804 и статистическую мощность (1 – β) = 0,5714.
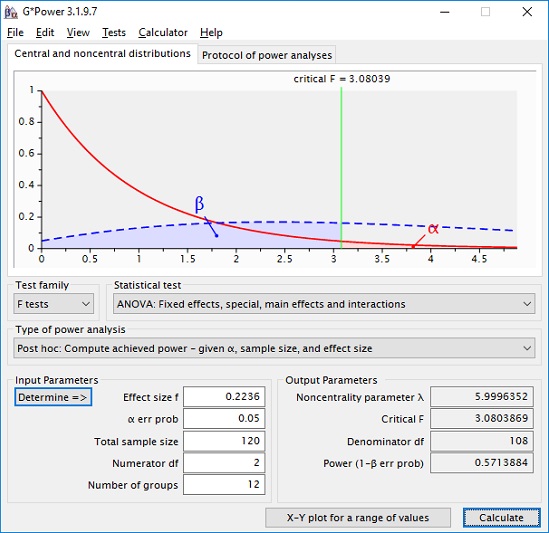
Рис. 9. Апостериорный анализ статистической мощности многофакторного F-теста
Для фактора B нужно указать df = kВ – 1 = 3, оставив остальные исходные данные без изменения. Параметр нецентральности не изменился λ = 5,9996, критическое F-значение F(3, 108) = 2,6887 и статистическая мощность (1 – β) = 0,5020. Если нас интересует эффект взаимодействия, то число степеней свободы df = (kA – 1)(kВ — 1) = 6. Критическое F-значение F(6, 108) = 2,1837, а статистическая мощность падает до 0,3806.
Анализ статистической мощности для тестов χ2
В психологических исследованиях обычно применяются два типа χ2-тестов: (а) тесты на непредвиденные обстоятельства (также называемые тестами независимости), оценивающие отклонения (H1) от стохастической независимости (H0) двух или более категориальных переменных и (b) тесты соответствия теоретического распределения экспериментальному. В обоих случаях вычисления статистической мощности основаны на нецентральном χ2-распределение. Его параметр нецентральности равняется произведению размера выборки N на квадрат индекса размера эффекта:
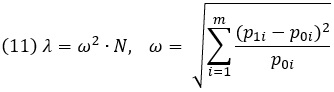
где m – количество категорий, p0i – вероятность категории i при H0, p1i – вероятность категории i при H1.
Рассмотрим пример теста на непредвиденные обстоятельства. Вероятность успеха терапии X довольно велика px = 0,88. К сожалению, терапия Х дорогая. Предположим, что новая терапия Y дешевле. Она будет применяться только в том случае, если ее успешность не (значительно) меньше, чем у терапии X. Эта ситуация соответствует гипотезе H0: py ≥ px против H1: py < px. Здесь подойдет односторонний χ2-тест на непредвиденные обстоятельства для таблицы 2 × 2. Тип терапии (X или Y) в строке, а результат терапии (успех или неудачи) – в столбце (см. рис. 10). Половине выборки назначается терапия X, второй половине – Y.
Мы хотим обнаружить недостаток терапии Y, предполагая, что вероятность недостатка высока. Другими словами, если статистический тест не выявит разницы между двумя методами лечения, мы хотим быть уверены, что на самом деле разницы нет. Следовательно, статистическую мощность выбираем (1 – β) = 0,95. С другой стороны мы принимаем на себя риск α = 0,20 к неправильному отклонению терапии Y как менее эффективной, чем X. По определению, мы будем называть терапию Y менее эффективной, чем X, только в том случае, если ее успешность меньше успешности X по крайней мере на 0,09. При частоте успеха для терапии X px = 0,88 это подразумевает вероятность успеха для терапии Y py = 0,88–0,09 = 0,79. Вероятности в ячейках таблицы непредвиденных обстоятельств 2 × 2, соответствующие этому описанию:
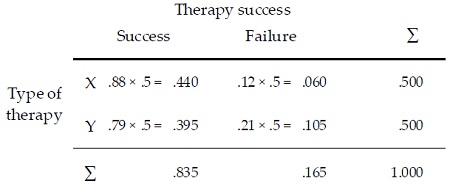
Рис. 10. Вероятности успеха и неудачи терапии Х и Y
Какой размер выборки N необходим? В GPower выбираем χ2-тест, Goodness-of-fit tests: Contingency tables, априорный тест.
Прим. Багузина. Этот комментарий также написан при участии Chat GPT. Тесты соответствия (goodness-of-fit tests) – это статистические тесты, которые используются для определения, насколько хорошо эмпирические данные соответствуют теоретической модели или распределению. Таблицы сопряженности (contingency tables) – это таблицы, используемые для анализа связи между двумя категориальными переменными. Они показывают, сколько наблюдений относятся к каждой комбинации значений этих переменных. Тесты соответствия на таблицы сопряженности используются для проверки того, насколько хорошо наблюдаемые частоты в таблице сопряженности соответствуют ожидаемым частотам, которые могут быть вычислены на основе некоторой теоретической модели или гипотезы. Например, можно проверить гипотезу о том, что две категориальные переменные независимы друг от друга, используя тест хи-квадрат (chi-square test) для таблиц сопряженности. Таким образом, Goodness-of-fit tests: Contingency tables, Тесты соответствия: таблицы сопряженности относятся к статистическим методам, которые используются для проверки того, насколько хорошо эмпирические данные, представленные в таблице сопряженности, соответствуют теоретической модели или гипотезе.
Устанавливаем α = 0,40 и (1 – β) = 0,95. Расчеты в GPower основаны на ненаправленном χ2-тесте. Для направленного теста выше мы указали, что готовы согласиться с ошибкой I-го рода α = 0,20. Для ненаправленного теста ошибку следует увеличить в два раза. Для расчета размера эффекта кликните Determine. Откроется дополнительное окно. Установите число ячеек = 4, введите данные в таблицу, как показано на рис. 11. Поскольку 50% выборки соответствует терапии X, а вторые 50% – терапии Y, вероятности в ячейках для H1 дают 0,880 * 0,5 = 0,440 и 0,120 * 0,5 = 0,060 для успеха и неудачи терапии Х. Аналогично для успеха и неудачи терапии Y: 0,790 * 0,5 = 0,395 и 0,210 * 0,5 = 0,105.
H0 предсказывает статистическую независимость от типа терапии при тех же средних. Это подразумевает одинаковую вероятность успеха (0,835 * 0,5 = 0,4175) и неудачи (0,165 * 0,5 = 0,0825) для обоих методов лечения. После того, как четыре ряда ячеек правой таблицы заполнены, кликните Calculate and transfer to main window. Получим значение эффекта размера ω = 0,1212. Укажите df = 1 в главном окне. Параметр нецентральности λ = 6,1731. Априорный анализ возвращает необходимое N = 420 и критическое χ2 = 0,7083.
Если статистика χ2 превысила критическое значение, и частота успеха выборки терапии Y была меньше, чем у терапии X, мы бы приняли H1. Новая терапия Y должна быть отвергнута. Если статистика χ2 не превышает критическое значение, H0 будет сохранена. Можно использовать менее дорогую терапию Y. Обратите внимание, что все вычисления являются приближенными, поскольку точное распределение статистики χ2 соответствует распределению χ2 лишь для асимптотического случая, то есть для N →∞. Однако при N = 420 отклонение от асимптотического распределения ничтожно мало.
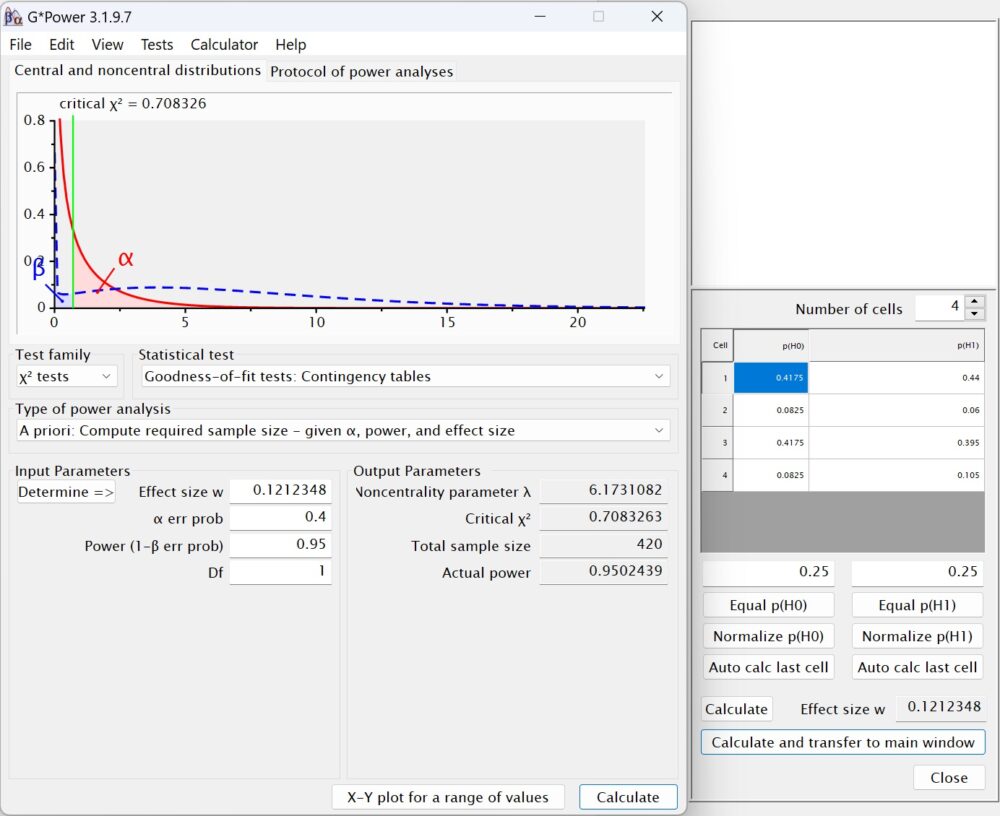
Рис. 11. Априорный анализ статистической мощности χ2-теста
Заключение
Анализ статистической мощности необходим для оценки статистических решений, а также для планирования исследований. GPower представляет собой простой в использовании программный инструмент, который облегчает реализацию различных видов анализа статистической мощности. Эта статья представила небольшое число наиболее часто используемых статистических тестов. Подробное руководство GPower охватывает 31 статистический метод. В руководстве описаны теоретические основы каждого метода и указания по использованию программы.
[1] В руководстве говорится о GPower версии 2. На момент публикации заметки доступна версия 3.1.9.7 от 17 марта 2020 г. Именно она использовалась при подготовке заметки и иллюстраций. – Прим. Багузина.