Основы теории вероятностей

Недавно прочитал книгу Вэй Цзи Ма. Байесовские модели восприятия и действия, и мне понравилось введение в теорию вероятностей, вынесенное в приложение. Кратко и оригинально.

Алгебра помогает понять математику, а теория вероятностей помогает понять жизнь. К сожалению, теория вероятностей не является стандартным компонентом большинства учебных программ бакалавриата. Мы надеемся, что это изменится, а пока предлагаем ознакомиться с некоторыми основами теории вероятностей. Это ни в коем случае не исчерпывающее введение, которое можно найти в учебнике по теории вероятностей. Это краткий справочник, который сосредоточен только на концепциях и расчетах, используемых в книге.

Скачать заметку в формате Word или pdf, примеры в формате Excel

Объективная и субъективная вероятности

Вероятность – это степень возможности. В самом узком смысле вероятность можно определить как ожидаемую частоту исхода повторяющегося события, например вероятность того, что монета выпадет орлом, или вероятность того, что кто-то выбросит 5 на игральном кубике. Эти события могут повторяться произвольно большое количество раз, и можно подсчитать частоты долгосрочных результатов. Если доля подбрасываний, при которых монета выпадает орлом, сходится к 0,5, по мере того как число подбрасываний приближается к бесконечности, мы можем утверждать, что монета имеет вероятность выпадения орла, равную 0,5. Этот тип вероятности иногда называют объективной вероятностью, и это единственный допустимый тип вероятности в соответствии со строгим частотным взглядом на вероятность.

Намного более широкое и, как мы полагаем, более полезное толкование вероятности – это степень веры в возможность исхода. Иногда ее называют субъективной вероятностью. Повседневные термины «уверенность» и «неопределенность» относятся к субъективным вероятностям. Если я знаю, что у кубика шанс выпадения 5 равен 1/6, то моя уверенность в том, что выпадет 5, равна 1/6. Этот конкретный пример тривиален, потому что он основан на простом преобразовании объективной вероятности (частоты долгосрочных результатов) в утверждение убеждения. Однако гораздо более широкая применимость субъективного толкования становится очевидной, когда мы рассматриваем степень уверенности в результатах, которые невозможно повторить, например вероятность того, что кандидат А победит кандидата B на предстоящих выборах.

Это не та вероятность, которую можно получить, повторяя одно и то же событие много раз, но тем не менее мы можем иметь надежное предсказание относительно результата. В самом деле, повседневная жизнь изобилует примерами субъективных вероятностей, которые нельзя сформулировать как частоты долгосрочных результатов: какова вероятность того, что сегодня пойдет дождь? Какова вероятность того, что мне понравится книга? Многие научные вопросы также можно сформулировать только в терминах субъективных, а не объективных вероятностей: какова вероятность того, что масса Сатурна находится между 10²⁵ и 10²⁶ кг? Какова вероятность того, что болезнь X вызвана вирусом?

Различие между объективной и субъективной вероятностями имеет долгую историю и не всегда очевидно. Например, чтобы определить вероятность того, что сегодня пойдет дождь, синоптик может запустить большое количество симуляций, начиная с текущего состояния атмосферы, каждая из которых использует разные экземпляры стохастических факторов в модели, и записать частоту дождливых дней в этой последовательности результатов запуска модели. Хотя результирующая вероятность является субъективной, она была получена «объективным» способом, а именно путем подсчета. Точно так же, если я наблюдаю на небе темные тучи и высказываю свое мнение о высокой вероятности дождя, я выражаю субъективное вероятностное суждение, но основываю это суждение на большом количестве ранее наблюдавшихся, подобных (хотя и неидентичных) состояний неба.

Байесовский вывод рассматривает субъективные и объективные вероятности одинаково: одни и те же математические отношения (правило Байеса, маргинализация и т. д.) одинаково применимы к обоим типам вероятностей. Поэтому байесовский вывод находит широкое применение. Однако байесовские модели восприятия основаны в основном на субъективной вероятности: существует только одно истинное состояние мира, но с точки зрения организма, пытающегося сделать вывод, существует множество возможностей, и этим возможностям можно присвоить степени уверенности.

Смысловое толкование вероятности

Мы называем множество всех рассматриваемых возможностей пространством событий. Событие или гипотеза – это подмножество пространства событий. Термин «событие» обычно используется при обсуждении объективной вероятности, а термин «гипотеза» – при обсуждении субъективной вероятности. Пространством событий могут быть «все возможные числа, которые я могу выбросить на кости» или «все возможные погодные условия, которые могут наблюдаться сегодня». Относительно первого пространства событием может быть выпадение четного числа. Относительно второго пространства можно рассматривать, например, гипотезу «сегодня будет дождь».

Вероятность события или гипотезы – это вещественное число от 0 до 1, указывающее степень вероятности события или гипотезы. Событие, которое гарантированно случается, имеет вероятность 1, а невозможное событие имеет вероятность 0. Для событий вероятность можно представить как частоту, с которой событие происходит среди очень большого числа случайных выборок из пространства. Например, вероятность выпадения четного числа на шестигранной кости равна 0,5. Эту вероятность можно также рассматривать как степень уверенности. К гипотезам понятие частоты обычно не применяется, но вероятность по-прежнему представляет собой степень уверенности; например, степень уверенности в том, что сегодня будет дождь, может быть равна 0,35. Мы обозначаем вероятность события или гипотезы X через p(X). Например, р(монета выпадет орлом) = 0,50.

Дополняющее событие

Для рассматриваемого события или гипотезы дополняющим событием или гипотезой является сценарий, при котором первое событие или гипотеза не имеет места или является ложным. Например, дополняющим событием к выпадению 1 на кубике является событие «выпадение 2, 3, 4, 5 или 6 на кубике». Если событие или гипотеза обозначены X, то их дополняющее событие или гипотеза обозначаются ¬X (читается «не X»). Здесь ¬ – символ логического отрицания. Вероятность дополняющего события или гипотезы равна 1 минус вероятность основного события или гипотезы: р(¬Х) = 1 – p(X).

В некоторых ситуациях легче рассчитать вероятность дополняющего события или гипотезы, чем самого события или гипотезы. Например, если вас просят вычислить вероятность того, что сумма очков на двух игральных костях не меньше 3, проще сначала вычислить вероятность того, что сумма очков меньше 3, и вычесть ее из 1 (ответ 35).

Представление в виде диаграммы Венна

События и гипотезы могут быть представлены графически с помощью диаграмм Венна. Строго говоря, площадные диаграммы, которые мы показываем в этой книге, являются диаграммами Эйлера, поскольку они представляют только отношения, которые действительно имеют мест. По определению диаграммы Венна представляют все возможные логические отношения между множествами. Однако мы следуем общепринятому соглашению называть любые площадно-вероятностные диаграммы диаграммами Венна.

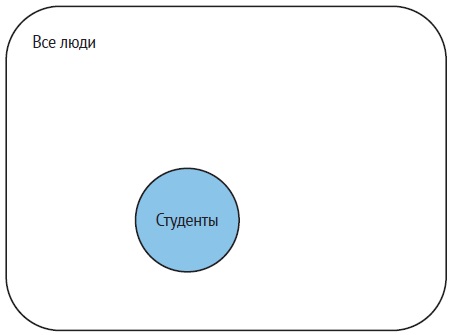
Рис. 1. Пример диаграммы Венна, используемой для представления вероятностей

Сначала нарисуем большой прямоугольник, внутренняя часть которого представляет все возможные результаты, то есть пространство выборки. Присвоим площади этого прямоугольника значение 1, представляющее суммарную вероятность 1. Затем нарисуем внутри этого прямоугольника круг, представляющий все результаты, согласующиеся с конкретным событием или гипотезой.

Например, прямоугольник может представлять всех людей в определенной группе, а круг – всех студентов среди них. Площадь, заключенная в круг, является частью площади, заключенной в прямоугольник; эта доля представляет собой вероятность события или гипотезы – в нашем примере вероятность того, что случайно выбранный человек является студентом. Дополняющее событие или гипотеза представлено точками, которые находятся внутри прямоугольника, но снаружи круга. Его площадь, деленная на площадь прямоугольника, представляет собой вероятность того, что случайно выбранный человек в группе не является студентом.

Случайные величины и их распределения

Случайная величина – это переменная, значения которой не могут быть известны с уверенностью. Примеры случайной величины: число, выпавшее на кубике, дата рождения человека, размер обуви случайного человека на вашей улице, время, которое требуется, чтобы добраться от дома до работы, количество избирателей, которые будут участвовать в предстоящих выборах, или цена акции завтра. Противоположностью случайной величине является переменная, значение которой достоверно известно. Примерами неслучайных величин являются количество планет между нами и Солнцем (две), количество дней в неделе (семь), отношение длины окружности к диаметру круга (π) и расстояние между двумя соседними сантиметровыми отметками на линейке (1 см).

Это не абсолютное различие. Переменные, которые кажутся неслучайными, могут быть подвержены шуму производства или измерения, что делает их случайными. Например, расстояние между двумя соседними отметками на линейке может слегка различаться, поскольку машина, производящая линейки, вероятно, была запрограммирована компьютером, который устанавливал отметки в сантиметрах. Однако числа, сгенерированные компьютером, имеют только конечное число знаков после запятой, возможно десять. Как следствие сантиметровые отметки никогда не достигнут фемтометровой точности.[1] Кроме того, краска, используемая для маркировки, не будет прилипать к поверхности одинаковым образом при изготовлении каждой линейки. Следовательно, расстояние между двумя соседними метками можно рассматривать как случайную величину. По причинам, подобным этим, может быть полезно рассматривать все переменные как случайные, только имеющие очень низкую неопределенность.

Случайность, также называемая изменчивостью, шумом или стохастичностью, часто является следствием недостатка знаний. Если бы перед броском кубика вам удалось каким-то образом записать точное положение, направление и скорость, с которой кость покидает руку, то вы смогли бы точно смоделировать взаимодействие кости с воздухом и столом и предсказать исход броска. Поскольку никому неизвестны значения всех этих переменных, результат броска кубика считается случайным. Существует ли истинная случайность – это философский вопрос, который выходит за рамки книги.

Сравнение дискретных и непрерывных случайных величин

Случайные переменные можно классифицировать по значениям, которые они могут принимать. Наиболее существенное различие наблюдается между дискретными и непрерывными случайными величинами. Дискретная случайная величина принимает набор значений, которые можно посчитать, даже если их может быть бесконечно много. Примерами могут служить количество детей в семье, количество потенциалов действия, запускаемых нейроном, количество ходов в шахматной партии, возраст человека, если его считать целыми годами, и идентичность произнесенного слова. Дискретная случайная величина, принимающая только два возможных значения, называется бинарной.

Непрерывная случайная величина принимает значения в континууме. Примерами являются длина отрезка, направление, в котором можно идти в открытом поле, время ожидания перед красным светом, скорость автомобиля и частота звука. Непрерывную переменную можно рассматривать как дискретную, но со значениями, поступающими с бесконечно малыми приращениями. Например, расстояние является непрерывной переменной, но когда его измеряют в миллиметрах, оно является дискретной переменной. В компьютерной программе истинно непрерывных переменных не существует; они всегда дискретизированы с конечной точностью.

Суммарная вероятность всегда равна 1

Суммарная вероятность всех возможных значений случайной величины равна 1. Эта сумма является отражением того факта, что возможности взаимоисключающие. Если увеличить вероятность одного значения, то вероятность хотя бы одного другого значения должна уменьшиться.

Дискретные распределения вероятности

Дискретные распределения вероятности – это функции, которые присваивают вероятность каждому возможному значению дискретной случайной величины. Распределение вероятности по дискретной случайной величине также называется функцией распределения массы вероятности. Дискретная случайная величина X, принимающая определенное значение x, является событием, обозначаемым p(X = x). Поскольку теперь мы варьируем x по всем его возможным значениям, мы получаем функцию от x. Это функция распределения массы вероятности, которую мы будем обозначать через p_X(x) или через p(x), если нет двусмысленности в отношении идентичности случайной величины: p_X(x) = p(X = x).

Это равенство означает, что функция распределения массы вероятности, вычисленная в точке x, равна вероятности того, что случайная величина примет это значение. Мы используем индекс X (верхний регистр) для обозначения случайной величины, а аргумент x (нижний регистр) – для конкретного значения этой случайной величины. Термин «масса» заимствован из физики. Грубо говоря, он основан на использовании материи как метафоры возможности (точки в пространстве событий). Чем больше вероятность события или гипотезы, тем больше масса «материи».

Например, пусть случайная величина X – это число, выпавшее на игральном кубике. Его возможные значения x равны от 1 до 6. Если кубик честный (шансы выпадения всех граней равны), вероятность каждого из этих значений равна 1/6, то есть p(X = x) = 1/6 для каждого x. Это пример дискретного равномерного распределения. Если кубик «нечестный», вероятность хотя бы двух значений будет отличаться от 1/6, и распределение больше не будет однородным.

Для дискретных случайных величин общая вероятность вычисляется путем суммирования всех возможных значений и в итоге должна быть равна 1. Это свойство записывается следующим образом:

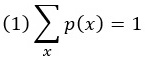
В конкретном случае, когда даны возможные значения X , мы можем поставить их выше и ниже знака суммы. Например, общая вероятность броска кости будет равна

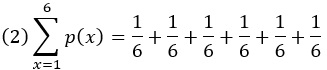
Бинарные случайные величины являются частным случаем дискретных случайных величин. Предположим, что бинарная случайная величина X может принимать значения x₁ и x₂. Мы знаем, что общая вероятность равна 1. Следовательно, вероятность x₂ равна 1 минус вероятность x₁, то есть p(X = x₂) = 1 – p(X = x₁).

Непрерывные распределения вероятности

Какова вероятность того, что рост человека точно равен 160 см? Она равна нулю, поскольку «точно» означает, что рост указан с точностью до бесконечного числа знаков после запятой. Эта проблема характерна для непрерывных случайных величин и говорит о том, что функции распределения массы вероятности, которые хорошо работали для дискретных распределений, должны быть заменены другим понятием, чтобы учесть свойства непрерывных переменных.

Предположим, нас интересует распределение вероятности роста взрослого человека (рис. 2). В первом приближении можно рассмотреть возможные значения в интервалах с шагом 10 см: от 120 до 130 см, от 130 до 140 см и т. д. С каждым интервалом связана вероятность, и таким образом мы можем построить функцию распределения масс вероятностей. Однако может возникнуть необходимость описать рост более точно, скажем в интервалах по 5 см: между 122,5 и 127,5 см и т. д. Таким образом, каждый исходный интервал заменяется двумя новыми, каждый из которых имеет в среднем половину вероятностной массы исходного интервала. Таким образом, новая функция распределения массы вероятности масштабируется примерно до половины высоты исходной.

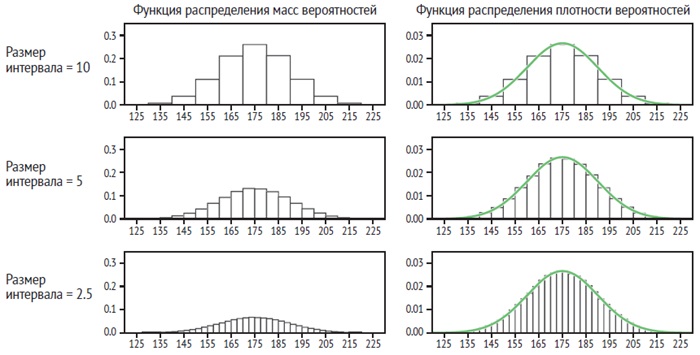
Рис. 2. Если случайная величина может принимать континуум значений (ось x), функция распределения массы вероятности определена только тогда, когда результаты разбиты по интервалам. Значения функции будут уменьшаться с уменьшением размера интервала (левый столбец). Функции распределения плотности вероятности получаются путем деления значений массы вероятности на размер интервала. Это дает значения, которые не зависят от размера интервала. Процесс уменьшения размера интервалов можно продолжать до тех пор, пока они не станут бесконечно малы. Получится непрерывная функция распределения плотности вероятности, показанная зеленым цветом

Поскольку мы продолжаем уменьшать ширину интервала, чтобы повысить точность, вероятностная масса на интервал также продолжает уменьшаться – она может стать сколь угодно малой. Это не очень хорошо. Есть ли способ предотвратить «исчезновение» массы вероятности? Да, это можно сделать, разделив массу вероятности в интервале на ширину интервала. При этом функция несильно меняется по мере уменьшения ширины интервала – она становится только более точной. Результатом этого процесса, когда ширина ячейки приближается к нулю (зеленая кривая), является функция плотности вероятности. Опять же, здесь просматривается аналогия с физикой: если вероятность в интервале рассматривается как масса, то деление этой вероятности на ширину интервала аналогично вычислению линейной плотности: масса на единицу длины оси x.

Сходство в обозначениях между функцией распределения массы вероятности для дискретных переменных и функцией распределения плотности вероятности для непрерывных переменных, которые записываются как p_X(x) или p(x), вводит в заблуждение, поскольку между ними есть некоторые важные концептуальные различия. Для дискретного распределения масса вероятности отдельной точки никогда не превышает 1, поскольку значения массы вероятности должны в сумме равняться 1. Для непрерывного распределения плотность вероятности в одной точке не имеет смысла и может принимать сколь угодно большие значения.

Рассмотрим, например, равномерное распределение на интервале [0, 0,01]. Оно будет иметь плотность вероятности 100 в каждой точке. Только интеграл по интервалу всегда будет меньше или равен 1. Иными словами, для дискретного распределения вероятность p(X = x) – это значимое число, которое может принимать любое значение от 0 до 1, и на самом деле тождественна р(х). Для непрерывного распределения p(X = x) всегда равна 0, и имеют смысл только вероятности вида p(a ≤ X ≤ b) с произвольными числами a и b. Например, вероятность того, что вы попадете абсолютно точно в центр мишени бесконечно тонким дротиком, равна 0.

Мы будем использовать такие термины, как функция распределения вероятности (probability distribution function, PDF), распределение вероятности или просто распределение для обозначения функции распределения массы вероятности дискретной случайной величины или функции распределения плотности вероятности непрерывной случайной величины.

Так же, как и для дискретных переменных, полная вероятность всех значений непрерывной переменной равна 1. Полная вероятность для непрерывной переменной вычисляется не как сумма, а как интеграл. Интеграл непрерывной функции плотности вероятности, как определено выше, представляет собой ширину интервала, умноженную на значение функции в этом интервале и суммированную по всем интервалам в пределе, когда ширина интервала приближается к нулю. В алгебре существуют методы вычисления интегралов определенных функций. Правило полной вероятности для непрерывной переменной X записывается как

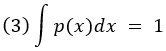
По сути, dx – это ширина очень маленького интервала (приращения), а знак интеграла – растянутая буква S от слова «сумма».

Наиболее важным непрерывным распределением является нормальное распределение, которое мы подробно обсудим ниже. Другим важным распределением является равномерное распределение. Равномерное распределение имеет постоянную плотность распределения на интервале [a, b]:

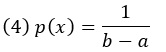
Существуют и другие распределения, широко распространенные в приложениях теории вероятностей. Экспоненциальное распределение задается выражением p(x) = λe^—^λ^x, где λ – константа, x – положительное вещественное число. Распределение по степенному закону задается как p(x) ∝ x^-a, где а – константа.

Формальное определение функции плотности вероятности

Рассмотрим непрерывную случайную величину X, такую как, например, время ожидания в очереди. Вероятность того, что значение X меньше или равно x, обозначается как p(X ≤ x). Это интегральная функция распределения (cumulative distribution function, CDF) X в точке x, обозначаемая P_X(x): P_X(x) = p(X ≤ x).

По определению это монотонно возрастающая функция, принимающая значения между 0 (при приближении x к 0) и 1 (при приближении x к ∞). PDF X теперь является производной этой функции:

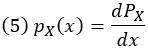
Пример CDF и PDF:

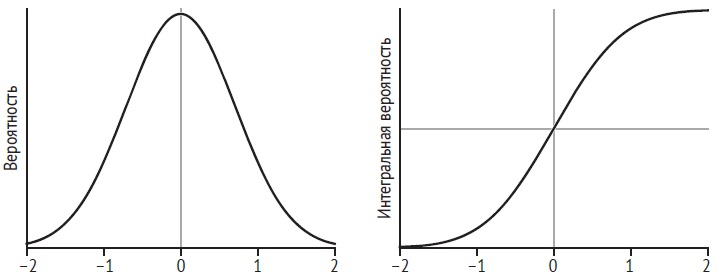
Рис. 3. Функция плотности вероятности и интегральная функция распределения

Чтобы вернуться из PDF в CDF, мы интегрируем:

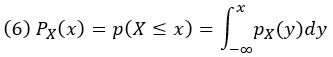
p_X(y) означает плотность вероятности случайной величины X, оцененную при значении y фиктивной переменной. Физический смысл этого выражения состоит в том, что интеграл по плотности представляет собой массу. Отсюда сразу следует, что вероятность того, что X принимает значения в интервале (x₁, x₂), может быть получена путем интегрирования p_X(x) между x₁ и x₂:

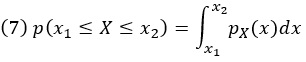
Нормирование

Функцию можно превратить в распределение вероятностей, разделив каждое значение на общее значение во всей области, при условии что это общее значение конечно. В результате распределение вероятностей будет интегрироваться (или суммироваться) до 1. Этот процесс называется нормированием. Если общее значение во всей области бесконечно, нормирование невозможно.

Упражнение B.1. Докажите, что экспоненциальное распределение нормировано.

Функция плотности вероятности экспоненциального распределения, определенного на области [0, ∞)

Интегральная функция экспоненциального распределения

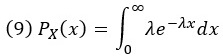
Интегрируем

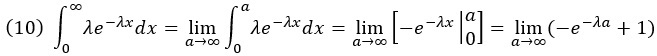
При а стремящемся к бесконечности –e^–^λ^a стремится к нулю. Таким образом интеграл (9) равен 1, что и требовалось доказать.

Упражнение B.2. Нормируйте степенное распределение p(x) = x^–a и найдите условие для a, при соблюдении которого возможно нормирование.

Итак, мы хотим проинтегрировать степенной закон:

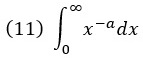
Исключим х = 0, так как в этой точке интеграл не сходится.

Произведем интегрирование:

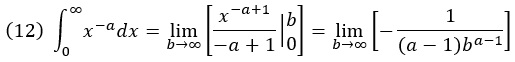
Если а > 1, то знаменатель уходит в бесконечность при b –> ∞, и весь предел равен нулю. Таким образом, интеграл сходится и равен некоторому конечному значению, что соответствует нормировке функции распределения.

Среднее значение, дисперсия и математическое ожидание

Для дискретной случайной величины X среднее или ожидание X равно

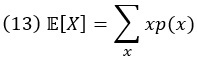
Дисперсия, которая является мерой разброса вокруг среднего, определяется как

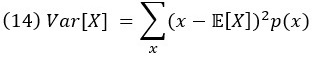
Стандартное отклонение – это квадратный корень из дисперсии. Среднее и дисперсия являются частными случаями математического ожидания любой функции случайной величины. Если мы обозначим функцию через f, то ожидание f равно

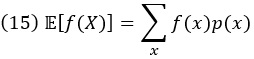
Таким образом, среднее значение является ожиданием X, а дисперсия равна

Для непрерывной случайной величины X с плотностью вероятности p(x) аналогичные выражения получаются заменой сумм интегралами:

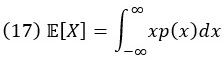
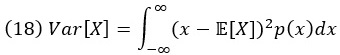
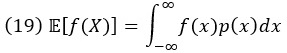
Как для дискретных, так и для непрерывных переменных существует общее эквивалентное выражение для дисперсии, а именно разность между средним значением квадратов и квадратом среднего:

Нормальное распределение

Наиболее важным непрерывным распределением в приложениях теории вероятностей является нормальное, или гауссово, распределение. Его функция распределения вероятностей имеет вид:

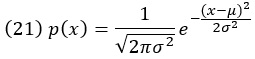
Иногда мы используем сокращенную запись p(x) = N(х; µ, σ²). Параметры µ и σ² не имеют априорного значения (они просто обозначены как предположение), но оказываются равными среднему и дисперсии распределения соответственно. Множитель перед экспонентой нужен для нормирования.

Стандартное нормальное распределение – это нормальное распределение со средним значением 0 и стандартным отклонением 1.

Центральная предельная теорема

Важность нормального распределения вытекает главным образом из центральной предельной теоремы. Говоря упрощенно, центральная предельная теорема утверждает, что среднее значение большого числа независимых случайных величин с идентичными распределениями вероятностей будет следовать приблизительно нормальному распределению, независимо от распределения исходных переменных. Вся мощь теоремы заключается в ее последней части: распределение исходных переменных не имеет значения. Ограничение теоремы можно смягчить, чтобы учесть независимые, но не одинаково распределенные переменные.

В математических моделях восприятия центральная предельная теорема всегда присутствует на заднем плане: всякий раз, когда мы предполагаем, что шум, искажающий стимул, распределен нормально, мы, по сути, обосновываем это с помощью центральной предельной теоремы. Случайная величина, которая описывает шум, искажающий стимул, может быть суммой большого числа независимых шумовых процессов.

Произведение двух нормальных распределений

Рассмотрим произведение двух гауссовых распределений вероятностей по одной и той же случайной величине X. У одного распределения среднее µ₁ и дисперсия σ₁², а у другого среднее µ₂ и дисперсия σ₂². Перемножим эти два распределения так же, как мы умножаем обычные функции, а затем нормируем результат (поскольку произведение не нормализуется автоматически). Каким будет итоговое распределение вероятности? Сначала запишем выражения для двух функций плотности вероятности:

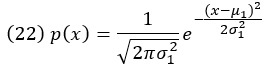
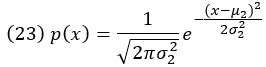
Умножение этих двух функций сводится к суммированию показателей степени. Сумма показателей степени

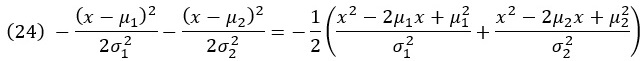
Выполним перестановку, сгруппировав все члены, содержащие x², и все содержащие x. Сумма показателей степени

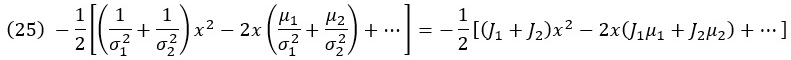
где мы используем следующие обозначения точности:

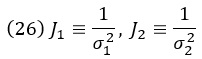
Кроме того, здесь и далее точками обозначены все слагаемые, не зависящие от x. При возведении в степень эти члены становятся постоянными множителями, не зависящими от x. Поскольку результат перемножения распределений должен быть нормирован в конце вычислений, любой постоянный множитель, который мы добавляем или оставляем до этого момента, не имеет значения.

Таким образом, произведение распределений (23 и 24) равно

(27)

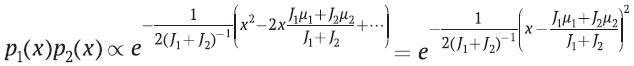
где знак пропорциональности поглощает все множители, не зависящие от x. Мы рассматриваем результат как другое нормальное распределение, теперь со средним значением

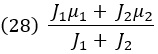
и дисперсией

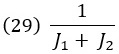
Интегральное нормальное распределение

Интегральная функция гауссова распределения не является элементарной функцией (то есть функцией, построенной из композиции таких элементарных функций, как степенные с любым действительным показателем, показательные и логарифмические, тригонометрические и обратные тригонометрические с использованием операций сложения, вычитания, умножения и деления). Однако у нее есть специальное название просто потому, что она часто встречается. Мы определяем интегральное распределение стандартной нормальной плотности вероятности как

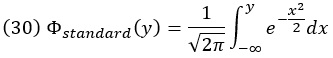
Эта функция принимает значения от 0 до 1.

Упражнение B.5. Покажите, что Ф_standard(0) = 0,5.

Распределение фон Мизеса

Некоторые переменные, такие как ориентация и направление движения, естественным образом имеют круговую (периодическую) область. Для таких переменных гауссово распределение не имеет смысла. Одним из решений является выбор распределения фон Мизеса. Его можно рассматривать как круговой аналог гауссова распределения. Оно имеет два параметра: круговое среднее и параметр концентрации, аналогичный обратной величине дисперсии гауссова распределения. Распределение фон Мизеса по круговой переменной s с областью определения [0, 2π), круговым средним µ и параметром концентрации k имеет вид:

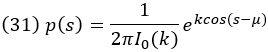
Здесь I₀ – модифицированная функция Бесселя первого рода порядка 0. Это так называемая специальная функция – определяемая через интеграл или бесконечный ряд. Для нас важно лишь то, что 2πI₀(k) нормирует распределение фон Мизеса. Когда k = 0, I₀(k) = 1, и распределение Мизеса становится равномерным на окружности. Чем выше k, тем больше распределение фон Мизеса похоже на нормальное распределение.

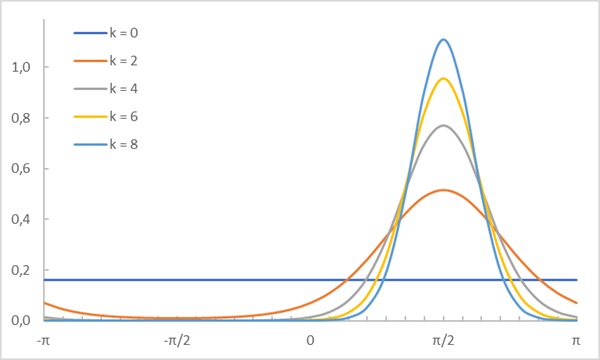
Рис. 4. Примеры распределений фон Мизеса. Область определения случайной величины является периодической. Для построения распределения в Excel использовалась формула(31), I₀(k) = БЕССЕЛЬ.I(k;0), µ = π/2

Упражнение B.7. Мы сказали, что µ – это круговое среднее, но как бы вы определили среднее значение для круговой переменной?

Вот что об этом думает ChatGPT. Круговое среднее представляет собой угол, который характеризует центр масс (центр распределения) круговых данных. Пусть у нас есть набор угловых данных Θ₁, Θ₂, …, Θ_т, измеряемых в радианах. Круговое среднее обозначается как µ и вычисляется по формуле:

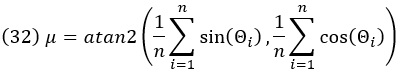
где atan2 – это функция арктангенса с двумя аргументами, что предотвращает проблемы с выбором квадранта.

Это выражение представляет угол, соответствующий центру массы всех угловых точек на круге. По сути, это среднее направление углов.

Упражнение B.8. Покажите аналитически, что в пределе больших k распределение фон Мизеса становится нормальным распределением. (Подсказка: используйте разложение косинуса в ряд Тейлора.) Кроме того, покажите, что точность этого нормального распределения равна k.

Рис. 5. Ответ ChatGPT на упражнение В.8

Дельта-функция

Случайная величина особого типа – это случайная величина, принимающая только одно возможное значение. Существует специальное обозначение распределения вероятностей такой случайной величины. Если X – непрерывная случайная величина, которая всегда принимает значение X = a, то ее распределение можно записать так: p(x) = δ(x – a).

Здесь δ – дельта-функция Дирака. Она возвращает 0, если аргумент не равен 0, а в ином случае возвращает бесконечность. Конечно, бесконечность не является числом, и поэтому дельта-функция Дирака, строго говоря, не является обычной функцией. Для нас это не имеет значения, поскольку единственное место, где мы будем использовать дельта-функцию, – внутри интеграла. Там любая функция f(x) обладает следующим свойством:

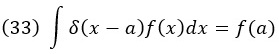
где мы предполагаем, что a входит в область интегрирования. Фактически уравнение (33) является определяющим свойством дельты Дирака. Дельта-функция равносильна вычислению функции f внутри интеграла в одной точке a.

Нам представляется удобным использовать для дискретных переменных те же обозначения, что и для непрерывных, т. е. писать δ(x – a) вместо δ_xa. Тогда дискретный аналог уравнения (33) имеет вид

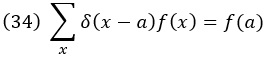
Распределение Пуассона

Дискретное распределение вероятностей, которое используем для описания нейронной активности, – это распределение Пуассона. Возможные значения случайной величины Пуассона: 0, 1, 2, 3, … (верхний предел отсутствует). Распределение Пуассона имеет свободный параметр λ. Распределение вероятностей X определяется выражением

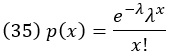
Распределение Пуассона является дискретным и определяется только целыми неотрицательными числами. Множитель е^–^λ действует как нормировочный. В отличие от х, λ не обязательно должно быть целым числом. Среднее значение и дисперсия переменной с распределением Пуассона равны λ.

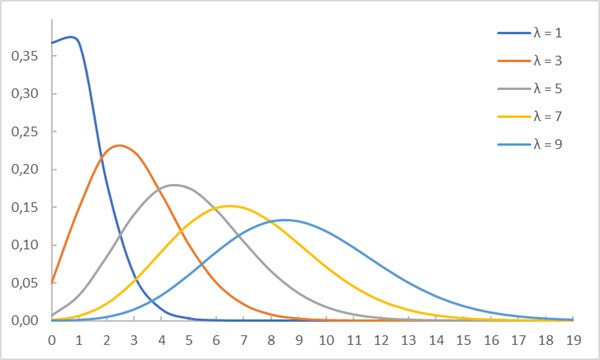
Рис. 6. Распределение Пуассона

Выборка из распределения вероятностей

В вероятностном моделировании нам часто приходится получать случайные числа в соответствии с заданным распределением вероятностей. Эти числа также называются выборками. На самом деле это отнюдь не тривиальная задача, но, к счастью, большинство программных пакетов имеют встроенные генераторы случайных чисел для наиболее распространенных распределений. Мы можем использовать эти функции для написания пользовательского кода, извлекающего из вероятностных распределений случайные значения, которые не были запрограммированы заранее.

Распределения, включающие несколько переменных

Для нас может представлять интерес зависимость случайных переменных друг от друга. Эта зависимость отражена в совместных и условных распределениях вероятностей, а также в правиле Байеса. Концепции, обсуждаемые в этом разделе, применимы как к непрерывным, так и к дискретным переменным. Таким образом, p может обозначать распределение либо массы вероятности, либо плотность вероятности. Поскольку мы рассматриваем несколько переменных одновременно, мы обычно будем использовать нижний индекс у p, чтобы обозначить, к какой случайной переменной(ым) принадлежит распределение вероятностей.

Совместная вероятность

Совместное распределение вероятностей случайных величин X и Y обозначается p_X,Y(x, y), или, сокращенно, p(x, y). Это вероятность значений x и y как пары. Суммирование по x и y дает 1:

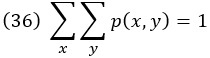
Для непрерывных переменных интеграл по обеим переменным равен 1:

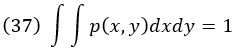
Совместная вероятность симметрична: p(x, y) = p(y, x)

Если X и Y представляют события, совместная вероятность X и Y – это вероятность того, что произойдут оба события, обозначаемая как p(X, Y) или p(X∩Y). В форме диаграммы Венна мы представляем Y в виде второй окружности, пересекающей первую. Совместная вероятность X и Y равна площади пересечения. Она всегда меньше или равна площади каждого отдельного круга. Это свойство выражают отношения p(X, Y) ≤ p(X) и p(X, Y) ≤ p(Y). Например, вероятность того, что в данный день идет дождь и вы будете на работе вовремя, меньше, чем вероятность того, что идет дождь. Эти отношения справедливы только для дискретных переменных.

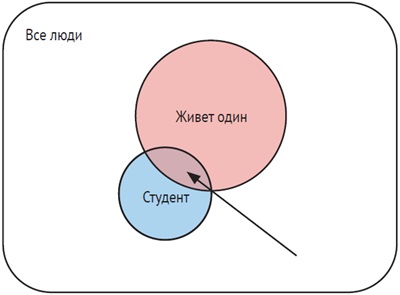
Рис. 7. Совместная вероятность событий «быть студентом» и «жить отдельно» представлена площадью пересечения, указанной стрелкой

Маргинализация

Представьте, что у вас есть кошка и собака. Вы тщательно отслеживаете, какова вероятность того, что в течение дня в гостиной находится только ваша кошка, только ваша собака, ни та, ни другая или они обе. Эти вероятности показаны в таблице, которая называется таблицей сопряженности (contingency table) и представляет вероятности совместных исходов. Предельные вероятности – это вероятности того, что кошка присутствует или отсутствует независимо от собаки, и вероятности того, что собака присутствует или отсутствует независимо от кошки.

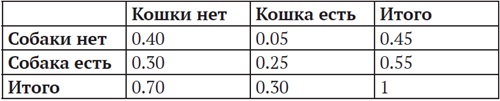
Рис. 8. Частоты сочетаний двух случайных величин

Маргинализация – это операция получения из совместного распределения по нескольким переменным распределения по подмножеству этих переменных. Например, если p(x, y) является совместным распределением X и Y, то суммирование по Y дает распределение только X:

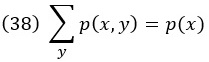
Аналог для непрерывных переменных получается заменой суммы интегралом:

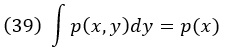
Это суммирование, или интегрирование, называется маргинализацией, потому что p(x) и p(y) называются маргиналами p(x, y). Если вы представляете (x, y) как точку в двумерном пространстве и совместное распределение обеспечивает z значений в этом пространстве, то маргиналы – это распределения, полученные путем суммирования по одному из измерений. Это приводит к двум одномерным распределениям, которые находятся на «краях» (margin) исходного двумерного распределения.

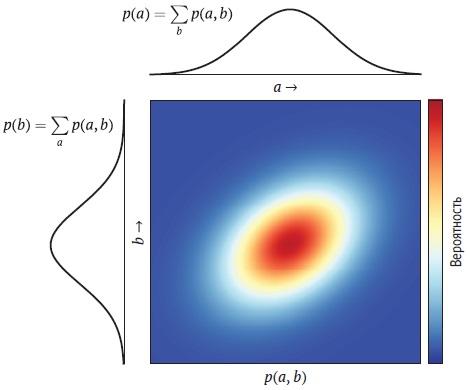
Рис. 9. Совместное распределение вероятностей двух случайных величин A и B. Черные кривые представляют маргиналы, полученные путем суммирования по одной из двух переменных

Условная вероятность

Для событий X и Y условная вероятность p(X|Y) является ответом на вопрос: «Из всех исходов, согласующихся с событием Y, какая часть также согласуется с событием X?» Условная вероятность события всегда находится между 0 и 1. В представлении диаграммы Венна вероятность p(X|Y) равна площади пересечения, деленной на площадь второго круга. Точно так же вероятность того, что произойдет Y, при условии что произойдет X, равна площади пересечения, деленной на площадь первого круга.

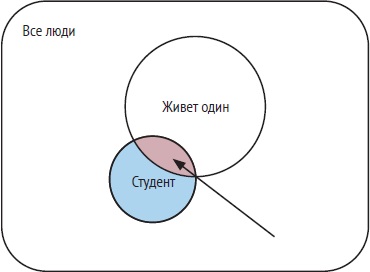
Рис. 10. Условная вероятность «живет один» при условии «является студентом» представлена площадью пересечения, деленной на площадь синего диска

Три примера условной вероятности:

вероятность того, что на кубике выпало 6, если выпало четное число, равна
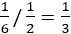
если вероятность того, что сегодня идет дождь и вы успеете на работу вовремя, равна 0,4, а вероятность того, что сегодня пойдет дождь, равна 0,5, то вероятность того, что вы придете на работу вовремя, при условии что идет дождь, равна 0,4/0,5 = 0,8;
в определенной стране в каждом штате разная доля водителей такси среди населения. Вероятность p(x|y) того, что человек, случайно выбранный из определенного штата, является водителем такси, равна доле граждан страны, которые живут в этом штате и являются водителями такси p(x, y), деленной на долю людей, живущих в этом штате p(y);

Из таблицы сопряженности (рис. 8) можно вычислить условные вероятности. Например, вероятность присутствия кошки при наличии собаки равна 0,25 (присутствуют и кошка, и собака), деленным на 0,30 + 0,25 = 0,55 (присутствие собаки).

Помните, что p(X|Y) не равно p(Y|X).

Если X и Y являются случайными величинами, распределение вероятностей X при заданном Y обозначается p_X|Y(x|y) или p(x|y), если нет неоднозначности в отношении переменных. Знак | читается как «обусловленный» или «при условии что». Он определяется как вероятность пары x и y, деленная на вероятность y:

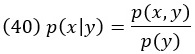
Упражнение B.9. Покажите, что p(x|y) нормирована как функция от x. Приведите пример, показывающий, что p(x|y) не нормируется как функция y.

Теперь объединим понятие маргинализации с определением условной вероятности.

Упражнение B.10. Покажите, что

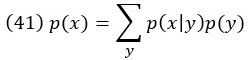
Интегральная форма этого уравнения:

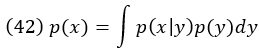
Продолжая пример с таксистом: предположим, вас интересует вероятность того, что случайно выбранный гражданин страны является таксистом. Вы знаете долю таксистов в населении каждого штата. Вы также знаете долю всех граждан, проживающих в каждом штате. Чтобы получить ответ, вы перемножаете эти две доли для каждого штата, а затем суммируете по всем штатам.

Мы можем обусловить каждую вероятность в уравнениях (38) и (41) третьей случайной величиной z. Тогда мы получаем:

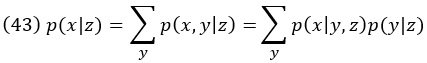
или в интегральной форме:

Условные распределения не ограничиваются одной случайной величиной до и после знака вертикальной черты. Например, можно рассмотреть распределение X и Y при заданных Z и W, обозначаемое как p(x,y|z,w).

Независимость

Две случайные величины X и Y называются независимыми, если их совместное распределение разлагается на маргиналы, т. е. если p(x,y) = p(x)p(y) для всех х и у. Например, вероятность того, что на кубике выпадет 6 и на монете выпадет орел, является произведением вероятностей обоих событий, взятых по отдельности. Независимость можно изобразить графически рис. 11). Можно реконструировать совместное распределение путем умножения маргиналов. Понятие независимости тесно связано с понятием корреляции: две независимые случайные величины также некоррелированы. Обратное неверно.

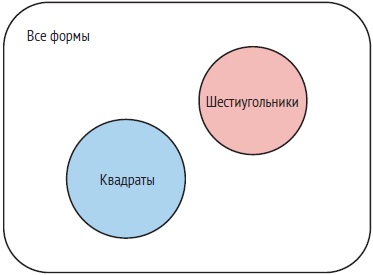
Рис. 11. Диаграмма Венна, изображающая независимость двух случайных величин

Упражнение B.11. Почему обратное неверно?

Упражнение B.12. Если X и Y независимы, что можно сказать об условных распределениях p(x | y) и p(y | x)?

Если X, Y и Z обозначают три случайные величины, то X и Y условно независимы при заданном Z, если p(x,y|z) = p(x|z)p(y|z) для любых значений x, y и z.

Правило Байеса

Правило Байеса связывает условные вероятности p(x|y) и p(y|x) друг с другом:

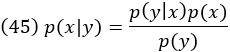
Здесь p(y|х) как функция х – функция правдоподобия по x, p(x) – априорное распределение по х, а p(x|у) – апостериорное распределение по х.

Доказательство. Из (40) мы знаем, что p(x,y) = p(x|y)p(y). Меняя местами x и y, мы также получаем p(y,x) = p(y|x)p(x). Совместная вероятность симметрична, т. е. p(x,y) = p(y,x). Из этих трех уравнений следует, что p(x|y)p(y) = p(y|x)p(x). Разделив обе части на p(y), мы получаем правило Байеса.

Упражнение B.14. Докажите, что правая часть уравнения (B.54) нормирована по x.

Рис. 12. Доказательство нормирования правой части уравнения Байеса от ChatGPT

Интерпретация диаграммой Венна правила Байеса для событий X и Y заключается в том, что площадь перекрытия может быть рассчитана двумя способами: как доля площади круга X, умноженная на площадь круга X, или как доля площади круга Y, умноженная на площадь круга Y. Поскольку результаты должны быть идентичными, это означает, что две дроби могут быть выражены друг через друга, если известно отношение площадей кругов X и Y.

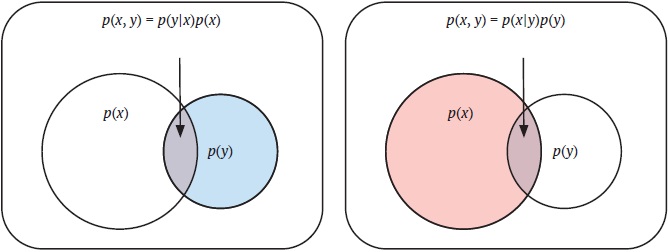
Рис. 13. Правило Байеса получается путем записи площади пересечения двумя разными способами и приравнивания двух выражений

Предположим, что 1 из 100 000 человек – профессиональный баскетболист, 1 из 100 человек – высокий и 95% профессиональных баскетболистов – высокие. Какова вероятность того, что высокий человек является профессиональным баскетболистом? Мы решаем эту задачу, применяя правило Байеса напрямую: если X – это «профессиональный баскетболист», а Y – «высокий рост», то p(X) = 0,00001, p(Y) = 0,01 и p(Y|Х) = 0,95. Отсюда следует, что p(X|Y) = 0,95 * 0,00001/0,01 = 0,0095, или примерно 1 из 1000. Еще раз: среди всех людей профессиональный баскетболист встречается 1 из 100 000 человек, а среди высоких – 1 из 1000!

Упражнение B.15. Докажите другую форму правила Байеса:

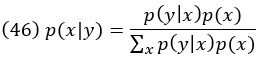
Последний способ записать правило Байеса — использовать знак пропорциональности: p(x|у)∝p(y|x)p(x).

Функции случайных величин

Функции одной переменной: изменение переменных

Если X – случайная величина с распределением вероятностей pX(x), а Y = f(X) – новая случайная величина, полученная путем применения функции или преобразования f к X, каково распределение Y? Например, X – равномерна распределена на [0, 1]. Y = X² – новая случайная величина, полученная путем возведения в квадрат результатов X. Каково распределение Y?

Простой, но неправильный ответ заключается в том, что поскольку X следует равномерному распределению, то и Y тоже. Если число x лежит между 0 и 1, возведение его в квадрат всегда будет давать меньший результат. Таким образом, хотя значения Y также будут лежать между 0 и 1, более низкие значения в этом диапазоне будут иметь большую плотность вероятности, чем высокие значения. Рассмотрим интегральные функции распределения X и Y, которые обозначим P_X(x) и P_Y(y):

Воспользуемся тем фактом, что плотность распределения вероятности PDF, обозначенная здесь как p_Y(y), является производной интегральной функции распределения CDF:

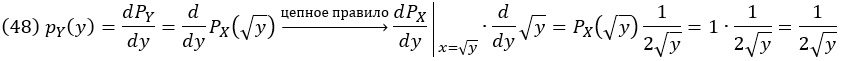
Результирующее распределение pY(y) нормировано (проверьте это) и соответствует нашему первоначальному предположению: плотность вероятности выше для более низких значений y. Проверим результат с помощью симуляции: возьмем множество случайных чисел из равномерного распределения между 0 и 1, возведем их в квадрат, и построим нормированную гистограмму квадратов с мелкими интервалами, а поверх нее проведем функцию (48):

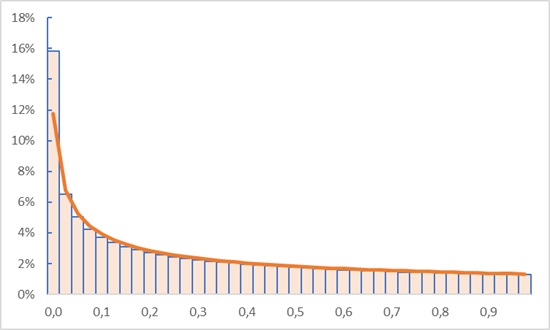
Рис. 14. Симуляция (гистограмма) и функция (48)

Мы могли бы сформулировать ту же задачу с произвольным распределением p_X(x) вместо равномерного. Вычисления идентичны, за исключением последнего шага. Далее мы находим, что

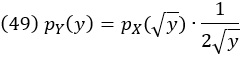
Таким образом, распределение квадрата переменной является произведением исходного распределения, оцениваемого по значению x, которое отображается в y, , и дополнительного множителя. Дополнительный множитель, называемый якобианом, равен производной отображения от y к x. Было бы неправильно не учитывать якобиан и утверждать, что p_Y(y) =

Якобиан фигурирует не только в этом примере возведения в квадрат случайной величины, но и в нашей первоначальной общей задаче. Предположим, что X – случайная величина с распределением вероятностей p_X(x) и Y = f(X), где f – монотонно возрастающая функция. Каково распределение Y? Сначала мы определим обратную функцию f^-1 как функцию от y, которая «отменяет» действие f, другими словами, f^-1(f(x)) = x. Эта обратная функция определена вполне обоснованно, поскольку мы предполагали, что f монотонно возрастает. Заманчивым, но неправильным способом получения распределения Y было бы подставить обратную функцию в p(X): p_Y(y) = p(X) (f^-1(y)) или предположить, что операция, применяемая к распределению, такая же, как и распределение, примененное к операции, p_Y(y) = f(p_X(y)). Правильный подход снова состоит в том, чтобы вычислить интегральное распределение Y:

и, следовательно, функция плотности вероятности y:

До сих пор мы рассматривали монотонно возрастающую функцию f. Когда f вместо этого монотонно убывает, окончательное выражение для p_Y(y) приобретает дополнительный знак минус.

Упражнение B.16. Покажите это.

Пример с яблоками

В качестве иллюстрации процедуры замены переменных предположим, что вы собираетесь посетить яблоневый сад. Вы очень мало знаете о том, как быстро растут яблоки, или о продолжительности вегетационного периода в этом регионе, и вы не знаете, какие яблоки растут в саду. Если друг спросит вас, какого, по вашему мнению, размера будут яблоки в саду, вы можете сначала ответить, что понятия не имеете. После более обстоятельных размышлений и на основе ограниченных знаний о яблоках в целом у вас возникает убеждение в однородном априорном распределении плотности вероятности по диаметру яблок в саду от 3 до 13 см. Какова же тогда ваша первоначальная плотность распределения относительно объема яблока?

Прежде чем мы получим ответ, давайте обсудим задачу. Равномерное априорное распределение относительно диаметра яблока означает, что, например, вы считаете равновероятным, что диаметр яблока будет лежать как между 5 и 6 см, так и между 10 и 11 см. Если мы аппроксимируем яблоки сферами, то объем яблока = πw³/6, где w – диаметр яблока. Таким образом, объемы, соответствующие диаметрам 5, 6, 10 и 11 см, равны (с точностью до целого числа) 65, 113, 524 и 697 см³. Это означает, что вы считаете равновероятным (точнее, с 10%-ной вероятностью), что объем яблока находится между 65 и 113 см³ (диапазон 48 см³), как и между 524 и 697 см³ (диапазон 173 см³). Таким образом, априорное распределение плотность вероятности относительно объема яблок отнюдь не плоское. Наоборот, плотность вероятности будет выше при меньших объемах.

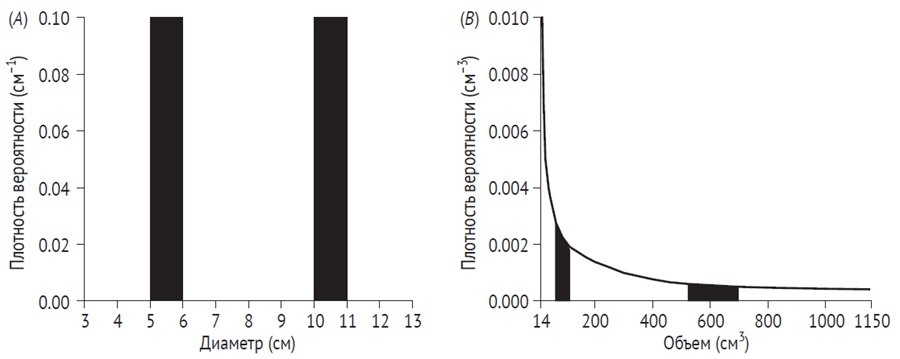
Рис. 15. Замена переменных: (A) равномерное априорное распределение вероятности для диаметра яблока от 3 до 13 см (диапазон 10 см). Априорное распределение плотности вероятности представляет собой линию высотой 0,1 см^-1, потому что общая площадь под плотностью должна быть равна 1. Вероятность того, что диаметр находится между 5 и 6 см, равна 0,1, как и вероятность того, что диаметр находится между 10 и 11 см (заполненные прямоугольные области); (B) априорное распределение плотности вероятности для объема яблока. Каждая закрашенная прямоугольная область – это вероятность того, что объем яблока находится в диапазоне, соответствующем диаметрам яблок, покрытым закрашенными прямоугольниками в A. Опять же, общая площадь под плотностью равна 1, а площадь каждого закрашенного прямоугольника равна 0,1 (обратите внимание на различия в масштабах по оси y)

Чтобы получить плотность вероятности по объему, мы отмечаем, что

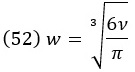
Для производной находим, что

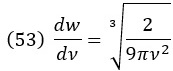
Следовательно:

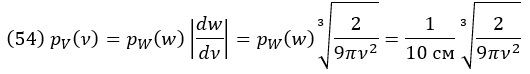
Это кривая, изображенная на рис. 15B.

Обязательство неведения

Интересное последствие процедур замены переменных, проиллюстрированное примером с яблоневым садом, состоит в том, что невозможно быть в неведении относительно всех нюансов задачи. Например, невозможно абсолютно ничего не знать о размере яблока в его общепринятом определении. Как вы только что видели, если мы заявляем, что ничего не знаем о диаметре яблока в том смысле, что принимаем равновероятным широкий диапазон диаметров, этим допущением мы демонстрируем определенное априорное знание объема яблока!

При выполнении байесовского статистического анализа исследователь может постараться включить как можно меньше априорных убеждений в анализ, о котором, по его мнению, у него почти нет соответствующих фоновых знаний. Как лучше всего это сделать, если, указывая на свое незнание параметра, он тем самым демонстрирует знание о связанных параметрах? Например, если исследователь «не знает» о стандартном отклонении σ случайной величины, он может выбрать использование плоского априорного значения в очень широком диапазоне σ, но тогда он неявно задает неравномерное априорное распределение для дисперсии σ². Поиск подходящих значений по умолчанию или эталонных априорных распределений для таких ситуаций является интересной темой в области байесовского статистического анализа. В байесовских моделях восприятия и действия это обычно не проблема, поскольку предполагается, что априорное значение получено либо из экспериментальной, либо из естественной статистики.

Функции нескольких переменных

Предположим, вы бросаете две игральные кости и складываете результаты. Каково распределение вероятностей суммы? Простой подсчет дает ответ: исход 2 может быть достигнут только одним способом (1 + 1) и, следовательно, имеет вероятность 1/36. Исход 3 может быть достигнут двумя способами (1 + 2 и 2 + 1) и, следовательно, имеет вероятность 2/36 и т. д. Это приводит к следующему распределению вероятностей:

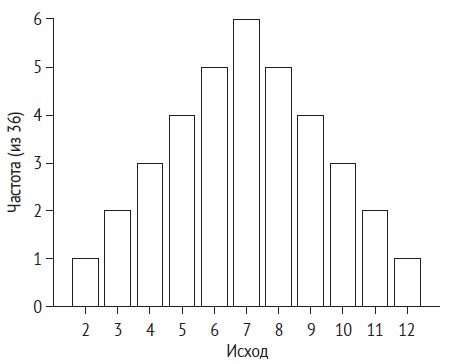
Рис. 16. Распределение вероятностей суммы двух бросков кости

Упражнение B.19. Если X и Y независимы и имеют равномерное распределение на [0, 1], вычислите распределение Z = X + Y. Ответ – частный случай распределения Ирвина-Холла.

Упражнение B.20. Если X и Y независимы и имеют нормальное распределение, докажите, что Z = X + Y также имеет нормальное распределение.

Задачи

Задача B.1. В цветнике 20% цветов составляют тюльпаны. Из них четверть красные. Какова вероятность того, что случайно выбранным цветком в этом саду окажется тюльпан, но не красный? Хотя эта задача легко решается с помощью логических рассуждений, примените формулы правил вероятности.

Задача B.2. Четыре игрока, сидящих вокруг стола, собираются сыграть в игру. Чтобы определить, кто начинает, один игрок бросает две кости. Сумма двух чисел определяет, кто начинает, при этом отсчет идет по часовой стрелке, начиная с бросающего кубик, которому присвоен номер 1 (таким образом, при сумме 5 или 9 начинает бросающий). Какова вероятность начать игру для каждого игрока?

Задача B.3. Вы и я бросаем кубик по одному разу.

Какова вероятность того, что у одного из нас выпадет 6, а у другого – нечетное число?
Какова вероятность того, что хотя бы у одного из нас выпадет 6?
Какова вероятность того, что у вас выпадет больше, чем у меня?
Какова вероятность того, что наша сумма больше 8?

Задача B.4. Вы учитесь в группе из тридцати человек.

Какова вероятность того, что день рождения конкретного одногруппника совпадает с вашим днем рождения?
Какова вероятность того, что день рождения хоть кого-то из одногруппников совпадает с вашим днем рождения?
Какова вероятность того, что у любых двух студентов совпадают дни рождения?

Задача B.6. Мы с вами поочередно подбрасываем монету. Вы начинаете. Если у вас выпадает решка, вы выигрываете. Если у вас выпадает орел, бросок переходит ко мне. Если у меня выпадает решка, я выигрываю. Если у меня выпадает орел, бросок снова переходит к вам. Игра продолжается до тех пор, пока один из нас не выиграет. Каков ваш шанс выиграть в этой игре?

Задача B.8. Эта задача связана с известным парадоксом Монти Холла. Вы участвуете в игровом шоу. Ведущий показывает вам три двери. За одной из них спрятан приз. Вы выбираете одну дверь (она остается закрытой). Ведущий, который знает, за какой дверью спрятан приз, открывает из оставшихся дверей ту, за которой нет приза. Затем ведущий дает вам возможность переключить свой выбор на оставшуюся неоткрытую дверь или остаться с вашим первоначальным выбором. Выбранная вами дверь открывается, и вы получаете приз, если он там есть.

Что нужно сделать, чтобы максимизировать вероятность получения приза?
Если есть N дверей и ведущий открывает m из них (где m < n – 1, какова вероятность получить приз при наилучшей стратегии?
Изменился бы ответ на вопрос (a), если бы ведущий не знал, в какой из двух оставшихся дверей находится приз, а в той, которую он открывает, случайно не оказалось приза? Обоснуйте свой ответ.
Подумайте, почему большинство людей считают, что не имеет значения, сохраните ли вы первоначальный выбор или выберете другую дверь.

Задача B.9. Функция плотности вероятности гауссовой случайной величины X задается уравнением 21. Покажите, что среднее значение и дисперсия этой случайной величины равны µ и σ² соответственно.

Задача B.10. Если X – экспоненциально распределенная случайная величина, где областью определения X является положительная вещественная числовая прямая, каковы область определения и распределение Y = e^X?

Задача B.11

Кто-то трижды подбрасывает честную монету. Вы наблюдаете за результатом одного броска, в котором выпадает орел. Какова вероятность того, что во всех трех подбрасываниях орел выпадет чаще, чем решка?
Кто-то подбрасывает честную монету N раз. Вы наблюдаете за результатом одного броска, в котором выпадает орел. Какова вероятность того, что во всех N подбрасываниях орел выпадет чаще, чем решка? (Для четного N интерпретируйте «больше» как «строго больше».)

Задача B.13. Если X и Y являются независимыми переменными со стандартным нормальным распределением, покажите, что случайная величина Z = Y/X имеет распределение Коши, т. е.

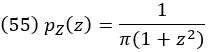
Задача B.14. Если X и Y независимы и имеют равномерное распределение вероятностей на [0, 1] (0 ≤ x ≤ 1), покажите, что произведение случайных величин Z = XY имеет распределение p_Z(z) = –log z. Убедитесь, что это распределение нормировано, хотя плотность в точке 0 равна бесконечности. Этот пример показывает, как распределение произведения может сильно отличаться от распределения каждого из множителей.

Задача B.15. Возьмем два распределения фон Мизеса для одной и той же случайной величины, одно со средним значением µ₁ и параметром концентрации k₁, другое со средним значением µ₂ и параметром концентрации k₂. Покажите, что нормированное произведение этих распределений снова является распределением фон Мизеса, и вычислите его среднее значение и параметр концентрации.

[1] Вот что пояснил ChatGPT по этому поводу. Фемтометровая точность означает измерение с точностью до фемтометра, что равно 10^-15 метра. Фемтометр (фм) – это единица измерения длины в системе Международных единиц (СИ), используемая для измерения очень маленьких объектов, таких как размеры атомных ядер или длины волн в высокоэнергетической физике. Точность в фемтометрах требует очень высокоточных измерительных приборов и методов, и она является одним из высших уровней точности в научных и инженерных измерениях.