Ранее мы рассмотрели два типа дискретных числовых распределений: биномиальное и гипергеометрическое. Во многих практически важных приложениях большую роль играет распределение Пуассона. Многие из числовых дискретных величин являются реализациями пуассоновского процесса, обладающего следующими свойствами:[1]
- Нас интересует, сколько раз происходит некое событие в заданной области возможных исходов случайного эксперимента. Область возможных исходов может представлять собой интервал времени, отрезок, поверхность и т.п.
- Вероятность данного события одинакова для всех областей возможных исходов.
- Количество событий, происходящих в одной области возможных исходов, не зависит от количества событий, происходящих в других областях.
- Вероятность того, что в одной и той же области возможных исходов данное событие происходит больше одного раза, стремится к нулю по мере уменьшения области возможных исходов.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Чтобы глубже понять смысл пуассоновского процесса, предположим, что мы исследуем количество клиентов, посещающих отделение банка, расположенное в центральном деловом районе, во время ланча, т.е. с 12 до 13 часов. Предположим, требуется определить количество клиентов, приходящих за одну минуту. Обладает ли эта ситуация особенностями, перечисленными выше? Во-первых, событие, которое нас интересует, представляет собой приход клиента, а область возможных исходов — одноминутный интервал. Сколько клиентов придет в банк за минуту — ни одного, один, два или больше? Во-вторых, разумно предположить, что вероятность прихода клиента на протяжении минуты одинакова для всех одноминутных интервалов. В-третьих, приход одного клиента в течение любого одноминутного интервала не зависит от прихода любого другого клиента в течение любого другого одноминутного интервала. И, наконец, вероятность того, что в банк придет больше одного клиента стремится к нулю, если временной интервал стремится к нулю, например, становится меньше 0,1 с. Итак, количество клиентов, приходящих в банк во время ланча в течение одной минуты, описывается распределением Пуассона.
Распределение Пуассона имеет один параметр, обозначаемый символом λ (греческая буква «лямбда») – среднее количество успешных испытаний в заданной области возможных исходов. Дисперсия распределения Пуассона также равна λ, а его стандартное отклонение равно ![]() . Количество успешных испытаний Х пуассоновской случайной величины изменяется от 0 до бесконечности. Распределение Пуассона описывается формулой:
. Количество успешных испытаний Х пуассоновской случайной величины изменяется от 0 до бесконечности. Распределение Пуассона описывается формулой:
где Р(Х) — вероятность X успешных испытаний, λ — ожидаемое количество успехов, е— основание натурального логарифма, равное 2,71828, X— количество успехов в единицу времени.
Вернемся к нашему примеру. Допустим, что в течение обеденного перерыва в среднем в банк приходят три клиента в минуту. Какова вероятность того, что в данную минуту в банк придут два клиента? А чему равна вероятность того, что в банк придут более двух клиентов?
Применим формулу (1) с параметром λ = 3. Тогда вероятность того, что в течение данной минуты в банк придут два клиента, равна
Вероятность того, что в банк придут более двух клиентов, равна Р(Х > 2) = Р(Х = 3) + Р(Х = 4) + … + Р(Х = ∞) . Поскольку сумма всех вероятностей должна быть равной 1, члены ряда, стоящего в правой части формулы, представляют собой вероятность дополнения к событию Х≤ 2. Иначе говоря, сумма этого ряда равна 1 – Р(Х ≤ 2). Таким образом, Р(Х> 2) = 1 – Р(Х≤2) = 1 – [Р(Х = 0) + Р(Х = 1) + Р(Х = 2)]. Теперь, используя формулу (1), получаем:
Таким образом, вероятность того, что в банк в течение минуты придут не больше двух клиентов, равна 0,423 (или 42,3%), а вероятность того, что в банк в течение минуты придут больше двух клиентов, равна 0,577 (или 57,7%).
Такие вычисления могут показаться утомительными, особенно если параметр λ достаточно велик. Чтобы избежать сложных вычислений, многие пуассоновские вероятности можно найти в специальных таблицах (рис. 1). Например, вероятность того, что в заданную минуту в банк придут два клиента, если в среднем в банк приходят три клиента в минуту, находится на пересечении строки X = 2 и столбца λ = 3. Таким образом, она равна 0,2240 или 22,4%.
Рис. 1. Пуассоновская вероятность при λ = 3
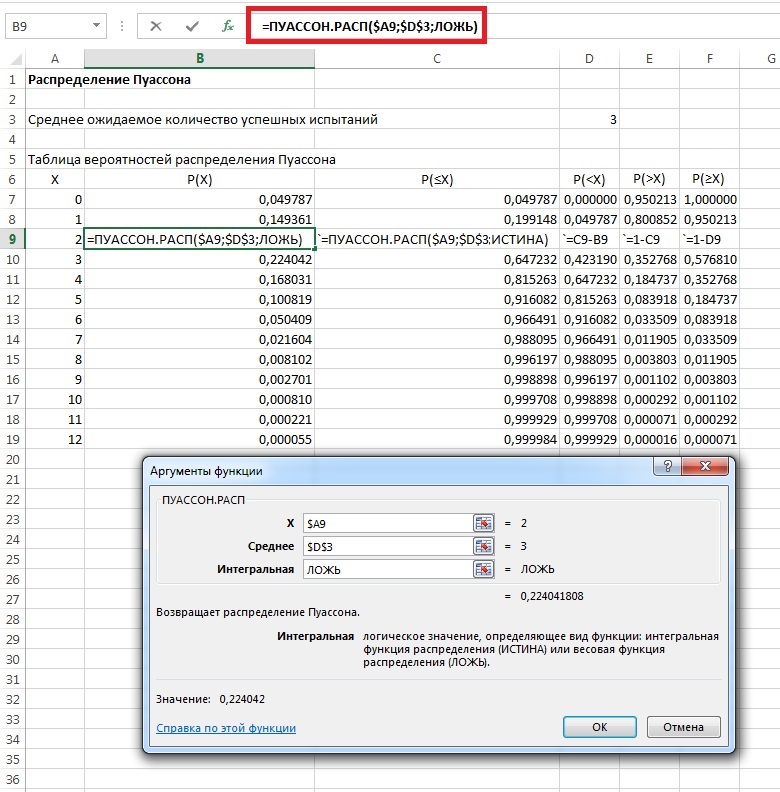
Сейчас вряд ли кто-то будет пользоваться таблицами, если под рукой есть Excel с его функцией =ПУАССОН.РАСП() (рис. 2). Эта функция имеет три параметра: число успешных испытаний Х, среднее ожидаемое количество успешных испытаний λ, параметр Интегральная, принимающий два значения: ЛОЖЬ – в этом случае вычисляется вероятность числа успешных испытаний Х (только Х), ИСТИНА – в этом случае вычисляется вероятность числа успешных испытаний от 0 до Х.
Рис. 2. Расчет в Excel вероятностей распределения Пуассона при λ = 3
Аппроксимация биномиального распределения с помощью распределения Пуассона
Если число n велико, а число р — мало, биномиальное распределение можно аппроксимировать с помощью распределения Пуассона. Чем больше число n и меньше число р, тем выше точность аппроксимации. Для аппроксимации биномиального распределения используется следующая модель Пуассона.
где Р(Х) — вероятность X успехов при заданных параметрах n и р, n — объем выборки, р— истинная вероятность успеха, е— основание натурального логарифма, X — количество успехов в выборке (X = 0, 1, 2, …, n).
Теоретически случайная величина, имеющая распределение Пуассона, принимает значения от 0 до ∞. Однако в тех ситуациях, когда распределение Пуассона применяется для приближения биномиального распределения, пуассоновская случайная величина — количество успехов среди n наблюдений — не может превышать число n. Из формулы (2) следует, что с увеличением числа n и уменьшением числа р вероятность обнаружить большое количество успехов уменьшается и стремится к нулю.
Как говорилось выше, математическое ожидание µ и дисперсия σ2 распределения Пуассона равны λ. Следовательно, при аппроксимации биномиального распределения с помощью распределения Пуассона для приближения математического ожидания следует применять формулу (3).
(3) µ = Е(Х) = λ = np
Для аппроксимации стандартного отклонения используется формула (4).
Обратите внимание на то, что стандартное отклонение, вычисленное по формуле (4), стремится к стандартному отклонению в биномиальной модели – , когда вероятность успеха p стремится к нулю, и, соответственно, вероятность неудачи 1 – р стремится к единице.
Предположим, что 8% шин, произведенных на некотором заводе, являются бракованными. Чтобы проиллюстрировать применение распределения Пуассона для аппроксимации биномиального распределения, вычислим вероятность обнаружить одну дефектную шину в выборке, состоящей из 20 шин. Применим формулу (2), получим
Если бы мы вычислили истинное биномиальное распределение, а не его приближение, то получили бы следующий результат:
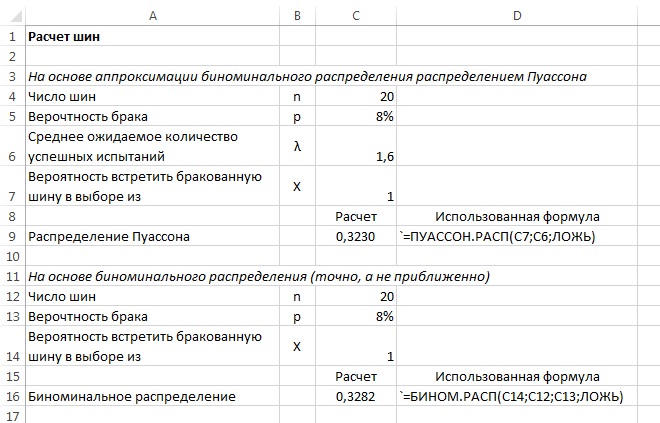
Однако эти вычисления довольно утомительны. В то же время, если вы используете Excel для вычисления вероятностей, то применение аппроксимации в виде распределения Пуассона становится излишним. На рис. 3 показано, что трудоемкость вычислений в Excel одинакова. Тем не менее, этот раздел, на мой взгляд, полезен понимаем того, что при некоторых условиях биномиальное распределение и распределение Пуассона дают близкие результаты.
Рис. 3. Сравнение трудоемкости расчетов в Excel: (а) распределение Пуассона; (б) биномиальное распределение
Итак, в настоящей и двух предыдущих заметках были рассмотрены три дискретных числовых распределения: биномиальное, гипергеометрическое и Пуассона. Чтобы лучше представлять, как эти распределения соотносятся друг с другом приведем небольшое дерево вопросов (рис. 4).
Рис. 4. Классификация дискретных распределений вероятностей
Предыдущая заметка Гипергеометрическое распределение
Следующая заметка Нормальное распределение
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 320–328

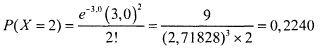
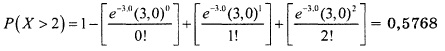


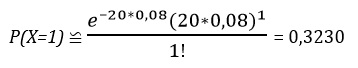
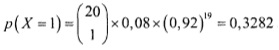

В рис.2 содержатся две опечатки:
1) В С3 д.б. $D$3, а не $F$3/
2) Наименования столбцов E6 и F6 следует поменять местами (д.б. P(>X) и P(>=X)).
Спасибо. Поправил
В строке «Применим формулу (1) с параметром X = 3.»
Не «Х» а гамма
Спасибо. Поправил.
Подскажите, пожалуйста, следующее. Как известно, для нахождение обратной функции нормального распределения есть функция в Excel НОРМ.СТ.ОБР(0,95)=1,65
А как вычислить для Распределения Пуассона?
Айгуль, в Excel нет функции обратной ПУАССОН.РАСП. На мой взгляд, дело здесь не в упущении разработчиков MS, а в том, что распределение Пуассона использует два целочисленных параметра: среднее и число испытаний. Как известно, подобрать целочисленные значения по функции очень непросто. В то же время нормальное распределение использует не целые параметры, так что нахождение обратной функции не составляет труда.
Прошу у всех прощения ,но это не комментарий, а попытка фиксации авторства частного лица. Суть дела в том, что мне, в результате самостоятельных изысканий, повезло обнаружить очень важное неизвестное до сих пор распределение, самое лучшее с точки зрения справедливости (я назвал его распределением Тертеряна) и математическую формулу, описывающее это распределение (она, эта формула, фундаментальна и проста). Разумеется, она не является формулой равенства. Она является формулой неравенства. Но неравенства справедливого. Моя формула справедливого неравенства найдет широкое применение для справедливого распределения доходов (вспомним грейдинг), для распределения налогов (вспомним нерешенную проблему расчета шкалы прогрессивного налога) и для решения других задач, связанных со справедливым и устойчивым распределением.
Тертерян Александр Сергеевич т. 8(916)052 84 96
E-mail: a.terter@yandex.ru
К сказанному выше хочу добавить, что для к-го интервала шкалы, разбитой на n интервалов, соответствующая доля этого к-го интервала от всего размаха шкалы составляет 0.234599684… В этом числе некоторые цифры сознательно искажены, но с определенной закономерностью известной только мне.