Недавно прочитал книгу Нассима Талеба Статистические последствия жирных хвостов. Книга о математике, лежащей в основе историй Талеба, рассказанных в его предыдущих эссе. Некоторые вопросы меня заинтересовали, и я решил остановиться на них подробнее. Заметка представляет собой смесь текста Талеба, моих моделей в Excel и кратких замечаний.
Начнем со среднеквадратического отклонения и дисперсии, как свойств высших моментов (точнее, вторых). Есть различие между среднеквадратическим отклонением и средним абсолютным отклонением, и это различие усиливается в случае жирных хвостов.
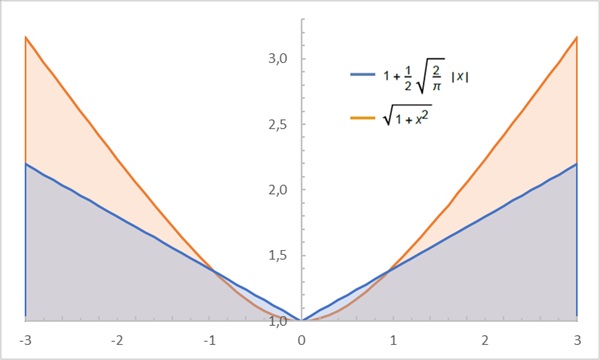
Рис. 1. Сравним поведение взвешивающих функций корень(K + x2) и K +|x|. При жирном хвосте среднеквадратическое отклонение расходится со средним абсолютным отклонением при больших значениях случайной величины х
Скачать заметку в формате Word или pdf, примеры в формате Excel
Примем для простоты, что среднее и медиана равны 0; тогда среднеквадратическое отклонение (Standard Deviation, STD):
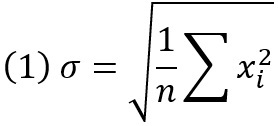
а среднее абсолютное отклонение (Mean Absolute Deviation, MAD):
![]()
Рис. 1 дает представление о том, как растет различие между этими статистическими моментами при больших средних отклонениях.
Обычные ошибки
Дэн Голдстайн и Насим Талеб задали следующий вопрос[1] профессиональным инвесторам и студентам выпускных курсов по финансовому инжинирингу — то есть людям, которые постоянно работают с рисками и отклонениями.
Акция (или фонд) имеет среднюю доходность 0%. Она изменяется в абсолютном выражении в среднем на 1% в день; рост в среднем составляет 1%, падение в среднем составляет 1%. Это не значит, что рост всегда 1 %, в некоторые дни рост 0,6%, в другие дни 1,45% и пр. Допустим, что мы живем в гауссовом мире, где доходность (или процент изменения за день) надежно моделируется нормальным распределением. Допустим, что в году 256 рабочих дней. Каково среднеквадратическое отклонение доходности (то есть процента изменения), параметр σAdj, характеризующий волатильность в финансовых прикладных программах? Каково среднеквадратическое отклонение за день? За год?
В условии задачи описано среднее абсолютное отклонение, а найти требовалось среднеквадратическое. Ответы на задачу в подавляющем большинстве оказались ошибочными. Почти все указали отклонение 1% в день. На самом деле гауссова переменная величина, которая за день изменяется в абсолютном выражении в среднем на 1%, имеет среднеквадратическое отклонение около 1,25%. В выборочных распределениях должно быть еще больше, до 1,7%. Про отклонение за год больше всего ответов было 16% или около того, что составляет около 80% от правильного ответа.
Профессиональные инвесторы для перехода от волатильности за день к волатильности за год умножали на корень из 256. Это дало бы правильный результат, если бы применялось к правильной оценке волатильности за день.
Итак, испытуемые были склонны сообщать MAD, когда их спрашивали о среднеквадратическом отклонении. Когда профессионалы финансовых рынков, постоянно слышащие, как обсуждают волатильность, говорят о «стандартном отклонении», они имеют в виду не среднеквадратическое отклонение, а среднее абсолютное, из-за чего недооценивают отклонения на 20–40%; для некоторых рынков недооценка может доходить до 90%. И когда им указывали на ошибку, мало кто из них понимал, что ошибся. При всем при том на просьбу выписать формулу среднеквадратического отклонения они успешно рисовали квадратный корень из среднего квадрата отклонения. Некоторые удивлялись, первый раз услышав от нас о существовании MAD.
Почему это важно: сложилась ситуация, где руководители, принимающие решения, рассуждают о «волатильности», имея о ней смутное представление. В финансовой печати отмечаем, что в ряде мест ту же ошибку делают и журналисты, пытаясь объяснить термин VIX (от volatility index, индекс волатильности). Даже на официальном сайте Министерства торговли США волатильность определена неверно.
Ошибка ведет к недооценке отклонений, потому что MAD, согласно неравенству Йенсена, меньше среднеквадратического отклонения (или равно ему). Для гауссовой случайной величины отношение ~ 1,25, а для жирных хвостов – больше.
Пример. Возьмем распределение с чрезвычайно жирным хвостом, в котором из n = 106 наблюдений одно-единственное показало миллион, а все остальные – минус единицу: X = {-1, -1, -1, …, 106}. Среднее абсолютное отклонение MAD(X) = 2. Среднеквадратическое отклонение STD(X) = 1000. Отношение среднеквадратического отклонения к среднему абсолютному отклонению = 500. Когда среднее арифметическое и медиана не равны, возникает вопрос, что подставлять в MAD? Талеб пишет, что обычно MAD центрируют вокруг медианы, но он считает, что для многих задач в теории принятия решений важнее видеть отклонения от среднего. Поэтому он центрирует MAD относительно среднего. Однако ChatGPT считает, что MAD центрируют относительно среднего арифметического:

Рис. 1а. ChatGPT о базе для расчета MAD
И в Excel функция СРОТКЛ() используют формулу, приведенную ChatGPT.
В примере выше MAD(X) = 2 получается также при центрировании относительно среднего арифметического.
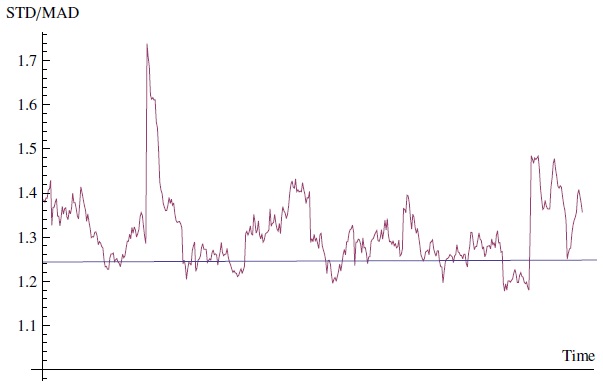
Рис. 2. Отношение STD/MAD для ежедневной доходности S&P 500 за последние 47 лет по скользящему временному окну 1 месяц. На уровень корень(π/2)≈1,253 (как приблизительное значение для гауссовых отклонений) можно смотреть как на точку отсечения жирнохвостости
Эффективность MAD и STD
Как полезную эвристику рассмотрим отношение h:
![]()
где Е – оператор математического ожидания (применяемый к исследуемому вероятностному параметру), и Х – центральная случайная величина, то есть Е Х = 0. h растет с ростом жирности хвостов распределения. Эффект недооценки волатильности по среднему абсолютному отклонению порождается выпуклостью вниз разности между этими функциями.
Почему в статистике предпочли STD, а не MAD? Читаем у Хьюбера:[2] был спор между Эддингтоном и Фишером, примерно в 1920 году, об относительных достоинствах dn (среднее абсолютное отклонение) и Sn (среднеквадратическое отклонение). Потом Фишер указал, что для в точности нормальных наблюдений Sn на 12% эффективнее (меньше), и, видимо, это решило исход спора.
Давайте реконструируем выкладки Фишера и поймем, что он имел в виду. Пусть n – число слагаемых. Асимптотическую относительную эффективность (Asymptotic Relative Efficiency, ARE) для гауссианы можно определить как
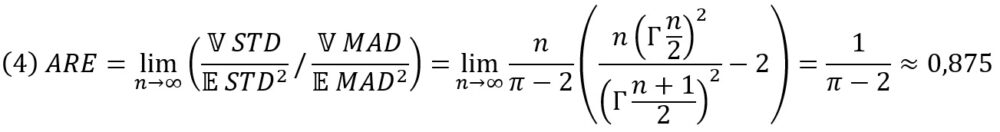
Здесь STD обозначает STD(X1, …, Xn) и MAD обозначает MAD(X1, …, Xn). То есть среднеквадратическое отклонение на 12,5% «эффективнее» среднего абсолютного отклонения, когда данные Гауссовы. Хотя от этого отношения ничего не останется при малейшем загрязнении данных. Ниже мы покажем как хрупко среднеквадратическое отклонение STD.
Влияние жирных хвостов на «эффективность» STD против MAD
Рассмотрим волатильность в обычной модели смешения, где с вероятностью р происходит случайное переключение на одно из двух распределений. Пусть они оба будут гауссовы и с математическим ожиданием 0; тогда и у модели математическое ожидание будет такое же. Дисперсию будем смешивать:
![]()
Для исследования модели используем метод Монте-Карло. Пусть загрязнение выбросами будет скромное, с вероятностью р = 0,01. На рис. 3 показано, что уже начиная с а = 2 ничего не остается от преимущества в эффективности у среднеквадратического отклонения по отношению к среднему абсолютному. С появлением выбросов MAD становится эффективнее, чем STD. Даже такие скромные «выбросы», как 5 сигм, делают MAD впятеро эффективнее, чем STD.
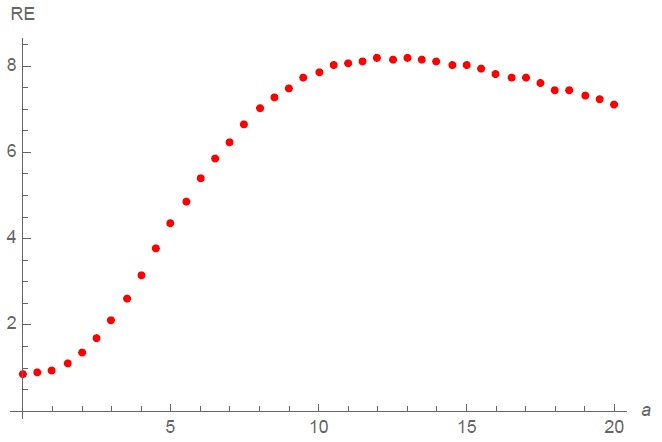
Рис. 3. Моделирование эффективности (Relative Efficiency, RE) среднеквадратического отклонения сравнительно со средним абсолютным отклонением, если подмешать в выборку выбросы величиной ![]() , где σ – среднеквадратичное отклонение
, где σ – среднеквадратичное отклонение
Случай Парето
Для стандартного распределения Парето с минимальным значением (и масштабом) L, плотностью вероятности f(x) = αLαx—α-1 и среднеквадратическим отклонением
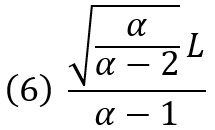
имеем
![]()
центрируя MAD относительно математического ожидания.[3]
Случайная величина Парето порождается средой, где неравномерности усиливаются до масштабов, сопоставимых с размерами всей среды; например, таково распределение богатства в условиях, когда действует принцип «деньги к деньгам».
Случайная величина X следует распределению Парето с коэффициентом масштаба L > 0 и коэффициентом формы, он же показатель степени хвоста α > 0, если X ∈ [L, ∞), то есть имеет минимальное значение L, и функция распределения имеет вид степенного закона
![]()
Плотность вероятности f(x) = αLαx—α-1 однохвостая с максимумом на краю х = L; среднее ∞ при α ≤ 1, иначе
![]()
дисперсия ∞ при α ≤ 2, иначе
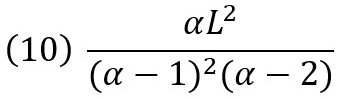
коэффициент асимметрии не существует при α ≤ 3, иначе
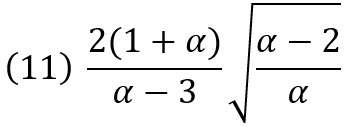
коэффициент эксцесса не существует при α ≤ 4, иначе
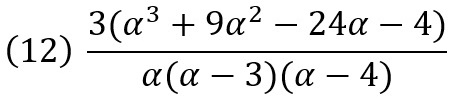
Бесконечные моменты
Любой бесконечный момент любого порядка, например бесконечная дисперсия, в наблюдаемой выборке проявляется как вычисляемая величина, то есть как конечный момент, просто потому, что выборка конечна. Скажем, распределение Коши, имеющее неопределенное математическое ожидание, в конечной выборке даст измеримое математическое ожидание; другое дело, что разные выборки будут давать совершенно разные математические ожидания. Следующие рисунки иллюстрируют «дрейф» моментов по мере поступления информации для стандартного распределения Коши
![]()
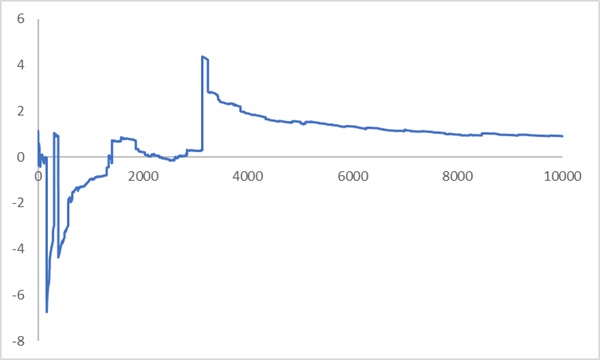
Рис. 4. Как изменяется среднее по выборке для последовательности данных, когда для их распределения (Коши) математическое ожидание не определено. В пределе fX(x) сходится к нулю… вот только выборки n = 10 000 не хватило…
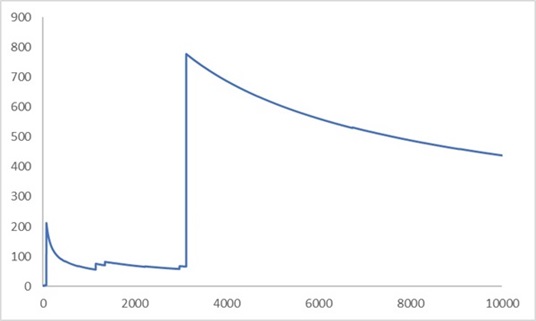
Рис. 5. Квадратный корень из второго момента выборки для последовательности данных, когда у их распределения бесконечная дисперсия. Наблюдаем кажущееся схождение, но только до очередного скачка
Почему среднеквадратическое отклонение нужно отправить в отставку, и немедленно!
Понятие среднеквадратического отклонения сбило с толку толпы ученых; пора отправить его в отставку из общего употребления и заменить на более эффективное среднее абсолютное отклонение. Среднеквадратическое отклонение следует оставить математикам, физикам и специалистам по математической статистике, выводящим предельные теоремы. Нет научных резонов рекомендовать его для статистических исследований в нашу компьютерную эпоху, ибо от него больше вреда, чем пользы — особенно когда растущий класс специалистов в общественных науках применяет готовые статистические инструменты к научным проблемам.
Скажем, пусть кто-то попросил вас оценить «среднее отклонение за день» для температуры в вашем городе (или биржевой стоимости компании, или артериального давления вашего дядюшки) на протяжении пяти последних дней. Данные об отклонениях в эти пять дней такие: (-23, 7, -3, 20, -1). Как вам оценить среднее отклонение?
Может быть, взять каждое наблюдение, возвести в квадрат, найти среднее по всем квадратам и извлечь из него квадратный корень? Или удалить знаки минус и посчитать среднее? Между этими двумя методиками серьезные различия. Первая оценит среднее отклонение как 15,7, а вторая — как 10,8. На самом деле вторая куда лучше соответствует «практическим задачам» и отражает реальность. Интуитивно мы часто ожидаем услышать именно о второй величине; нередко человеку сообщают среднеквадратическое отклонение, а он затем действует так, будто принял эту величину за среднее отклонение.
Причиной всему историческая случайность: в 1893 великий Карл Пирсон использовал термин «стандартное отклонение» (standard deviation) вместо употреблявшегося более громоздкого «среднеквадратическая ошибка» (root mean square error). И положил начало великому заблуждению: публика решила, что это значит среднее абсолютное отклонение. Предрассудок пустил корни и затвердел, как скала; всякий раз, кода какая-нибудь газета пыталась уточнить понятие рыночной «волатильности», она сбивалась в словесных описаниях на среднее абсолютное отклонение, даже если приводила формулу, по которой насчитала среднеквадратическое отклонение, более высокое.
И если бы только журналисты; аналогичное смешение можно увидеть в официальных документах Министерства торговли США и Федерального резерва — в заявлениях о рыночной волатильности, сделанных регуляторами рынка.
Вот что натворил неудачный термин для неинтуитивного понятия. Психологический феномен – склонность к упрощению – толкает людей принимать STD за MAD, потому что о MAD легче думать. Вот аргументы Талеба за революцию.
- MAD точнее оценивается по выборке и менее волатильно, чем STD, поскольку не взвешивает наблюдения, тогда как среднеквадратическая ошибка приписывает большим отклонениям больший вес, переоценивая хвостовые события. Мы часто используем STD в формулах, но в итоге приходим к необходимости преобразовать его в MAD (скажем, в финансах — для определения стоимости опциона). Поправка существенная. В Гауссовом мире STD примерно в 1,25 раза больше MAD. Но нам надо выживать при стохастической волатильности, где STD нередко превосходит MAD в 1,6 раза.
- Многие статистические явления и процессы характеризуются «бесконечной дисперсией» (то же знаменитое правило Парето 80/20), хотя обладают конечным и часто спокойно ведущим себя средним абсолютным отклонением. Во всех случаях, где существует STD, существует и MAD. Риска бесконечного MAD при конечном среднеквадратическом отклонении не существует.
- Многие экономисты побоялись рассмотреть модели с бесконечной дисперсией, додумав, что это значит бесконечное среднее абсолютное отклонение. Прискорбно, но факт. Когда великий Бенуа Мандельброт выдвинул свои модели с бесконечной дисперсией пятьдесят лет назад, экономисты испугались, потому что в их головах смешалось одно с другим.
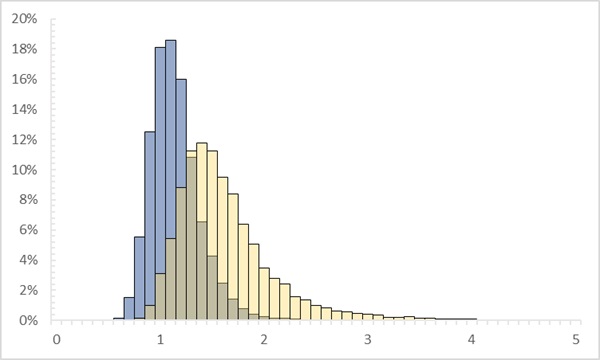
Рис. 6. Как распределено среднее абсолютное отклонение (синим) и среднеквадратическое отклонение (желтым), если исходное распределение следует степенному закону с конечной дисперсией
В качестве модельного я взял распределение Стьюдента с α = df = 3. Как обычно, у MAD более узкое распределение; в данном случае его даже трудно сравнить с распределением STD, имеющим бесконечную дисперсию (потому что квадрат случайной величины, распределенной по Парето с показателем α, распределен по Парето с показателем α/2). Можно, впрочем, сравнить распределения MAD и STD по их среднему абсолютному отклонению: у распределения STD оно в 2 раз больше.
Печально, что такая мелочь способна создать столько путаницы. Наши научные инструменты вышли далеко за нашу бытовую интуицию, и это стало проблемой для развития науки. В завершение приведу заявление сэра Роналда Фишера: «Статистик несет ответственность за понимание процедуры, которую применяет или рекомендует».
[1] Daniel Goldstein and Nassim Taleb. We don’t quite know what we are talking about when we talk about volatility. Journal of Portfolio Management, 33(4), 2007.
[2] P. J. Huber. Robust Statistics. Wiley, New York, 1981.
[3] Формула (7) отличается в оригинале и переводе, и я склонен больше верить версии перевода. Вообще, можно отметить, что перевод выполнен на очень высоком уровне с интересными комментариями и дополнениями.