Эта продолжение перевода книги Джерарда Вершурена. 100 симуляций в Excel
Предыдущий раздел К содержанию Следующий раздел
Глава 9. Честная монета
Что делает симуляция. Имитирует шестикратное подбрасывание монеты. В диапазоне С2:F8 подсчитывается теоретическая вероятность выпадения нуля решек, одной решки, и т.д. Подсчеты делаются для честной монеты с вероятностью выпадения решки в одном броске = 50%, и для нечестных монет, с вероятностью выпадения решки при однократном бросании = 20%, 30%, 40%. График для честной монеты представляет собой колоколообразную кривую. Максимум приходится на 3 решки и его теоретическая вероятность составляет 31% (ячейка F5). Для нечестных монет графики плотности вероятности имеют положительную асимметрию: пик сдвинут влево, а правый хвост более длинный, чем левый.
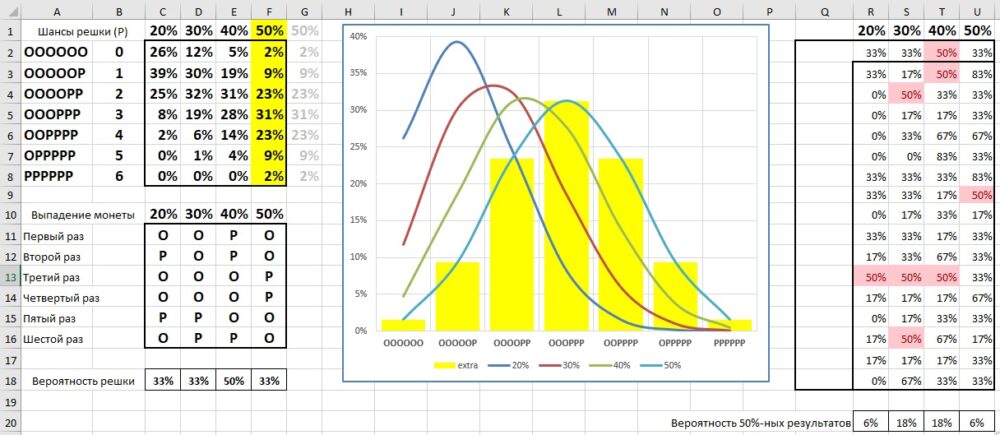
Рис. 2.1. Является ли монет честной? Чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Скачать заметку в формате Word или pdf, примеры в формате Excel
События со случайными исходами обладают тем свойством, что ни один конкретный исход не известен заранее. Однако если наблюдать множество исходов, то можно выявить закономерности. Когда мы подбрасываем честную монету, мы не знаем, какой стороной она упадет, но если мы подбросим монету миллионы раз, мы знаем, что она приземлится решкой очень близко к 50% случаев, если только…
…монета не имеет предпочтений. Здесь они смоделированы заданием более низкой вероятности выпадения решки. Чтобы определить, справедлива монета или нет, нам нужно было бы подбросить монету много раз. В этой симуляции мы делаем только шесть бросков в каждой серии. Поэтому для некоторых серий даже при вероятности решки 50:50 мы можем получить небольшое число серий, где эта вероятность воплотилась в нужный результат – около 31%. В ситуации, показанной на рис. 2.1, мы, вероятно, объявили бы честную монету несправедливой (см. значение в ячейке U20). Всего в одной серии число решек было равно трем. Статистики называют это ошибкой первого типа: мы сделали вывод, что монета нечестная, хотя на самом деле она честная. И наоборот, мы могли объявить монеты № 2 и 3 (ячейки S20 и Т20) честными. Это ошибка II типа: мы делаем вывод, что монета честная, хотя на самом деле она нечестная. Очевидно, что шесть подбрасываний недостаточно для надежных заключений.
Что вам нужно знать. Колоколообразная кривая очень часто встречается в статистике. Она отражает нормальное распределение. Чтобы изобразить эту кривую для двоичной ситуации (да/нет, орел/решка, успех/неудача) отлично подойдет функция Excel БИНОМ.РАСП(). Кстати, все функции в Excel состоящие из двух сокращений, разделенных точкой, где вторая часть РАСП – это статистические функции, возвращающие вероятность. Кроме упомянутой функции, это также: НОРМ.РАСП(), СТЬЮДЕНТ.РАСП(), ПУАССОН.РАСП() и многие другие.
Что вам нужно сделать. В ячейке C2 введите: =БИНОМ.РАСП($B2;6;C$1;0). Формула вернет значение биномиального распределения для нуля успехов (значение в В2) при шести испытаниях и вероятности успеха в одном испытании равного 20% (С1). Обратите внимание на использование смешанных ссылок. Они введены, чтобы можно было протащить формулу на диапазон С3:F8.
В столбце F вероятность выпадения решки 50%, и максимум кривой соответствует трем успехам (ячейка F5). Это честная монета. В других столбцах вероятность выпадения решки в одном испытании меньше (от 20% до 40%). Максимум кривой смещен влево. Т.е., решка будет выпадать реже.
В ячейке C11 мы имитируем первой бросок монеты: =ЕСЛИ(СЛЧИС()<=C$10;"Р";"О"). Скопируйте эту формулу на диапазон С11: F16.
В C18 мы подсчитываем процент решек: =СЧЁТЕСЛИ(C11:C16;"Р")/6. Скопируйте формулу в С18:F18.
Мы ожидаем, что значение в ячейке F18, соответствующее честной монете, составит 50%. Поскольку мы подбрасываем монету только 6 раз, появляется шанс, что результат может отличаться.
Мы повторим серию из 6 подбрасываний монеты еще 16 раз с помощью Таблицы данных. Введите формулы в R2: =C18, S2: =D18, T2: =E18, U2: =F18. Выделите диапазон Q2:U18. Пройдите по меню Данные –> Анализ "что, если" –> Таблица данных. Оставьте поле Подставлять значения по столбцам в: пустым, а в поле Подставлять значения по строкам в: щелкните на любую пустую ячейку, например W3. Это создаст в диапазоне Q3:U18 формулу массива: {=ТАБЛИЦА(;W5)}. Почему это работает см. предыдущий раздел.
В ячейке R20 подсчитайте вероятность серий, в которых было 50% решек: =СЧЁТЕСЛИ(R2:R18;0,5)/17. Скопируйте на ячейки R20:U20.
В R2:U18 создайте условный формат, чтобы подсветить ячейки со значением 50%.
Обратите внимание, как непросто решить, справедлива монета или нет.
Глава 10. Среднее средних
Что делает симуляция. Каждая выборка представляет собой 10 случайных целых чисел в диапазоне от 0 до 10. Например, первая выборка в ячейках В2:К2. Среднее значение выборки в L2. В ячейке L22 подсчитано среднее 20 средних значений по выборке. Именно значение в L22 и называется среднее средних. В столбцах N и O расположена таблица частот средних по выборке. Эта таблица выведена на график. Среднее средних представлено на графике вертикальной линией.
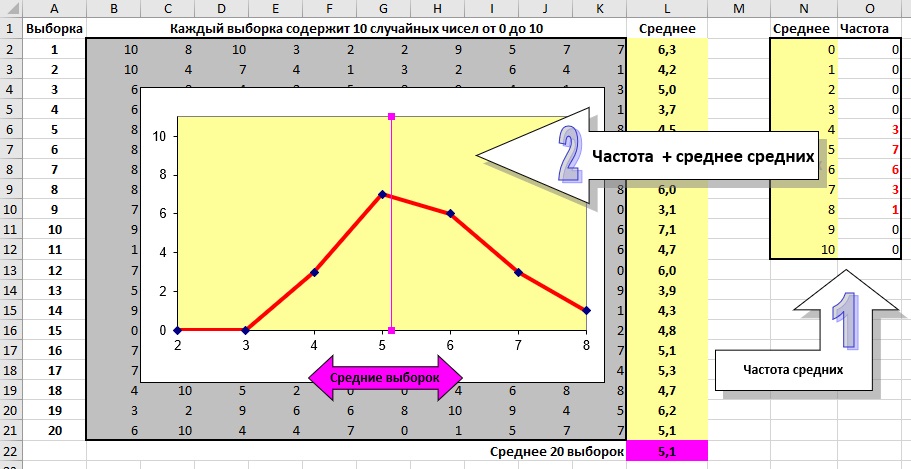
Рис. 2.2. Распределение средних значений выборок
Что вам нужно знать. Каждый раз, когда вы нажимаете Shift+F9, Excel пересчитывает все случайные числа, средние по выборке и среднее средних. Обратите внимание, как средние значения в столбце L довольно сильно разнятся, потому что каждое из них основано на выборке всего из 10 случайных чисел. А вот среднее средних меняется не сильно, так как оно основано на 10*20 = 200 случайных числах. В статистике это называется законом больших чисел.
Обратите также внимание, что средние значения распределены нормально (хотя и не идеально). И это при том, что сами случайные числа распределены равномерно. А это свойство известно в статистике, как центральная предельная теорема. Еще раз: независимо от того, какое распределение управляет отдельными значениями, средние значения выборок распределяются нормально!
Что вам нужно сделать. Введите в ячейку B2 формулу динамического массива: =СЛМАССИВ(20;10;0;10;ИСТИНА). В ячейке L2 вычислите среднее значение первой выборки: =СРЗНАЧ(B2:K2). Скопируйте формулу в L2:L21. В ячейка L22 найдите среднее из средних: =СРЗНАЧ(L2:L21). В ячейку O2 введите формулу динамического массива: =ЧАСТОТА(L2:L21;N2:N11). Как было показано в предыдущем разделе второй аргумент функции включает все интервалы, кроме последнего (N12). Графике основан на таблице частот. Вертикальная линия на графике представляет среднее средних и основана на наборе координат, скрытых в ячейках N15:O16.
Глава 12. Нормальное распределение
Что делает симуляция. В столбце A сгенерированы 100 случайных чисел со средним 0 и стандартным отклонением 1, распределенные нормально. В столбце D представлено частотное распределение этих случайных чисел, а в столбце Е теоретические значения для стандартного нормального распределения.
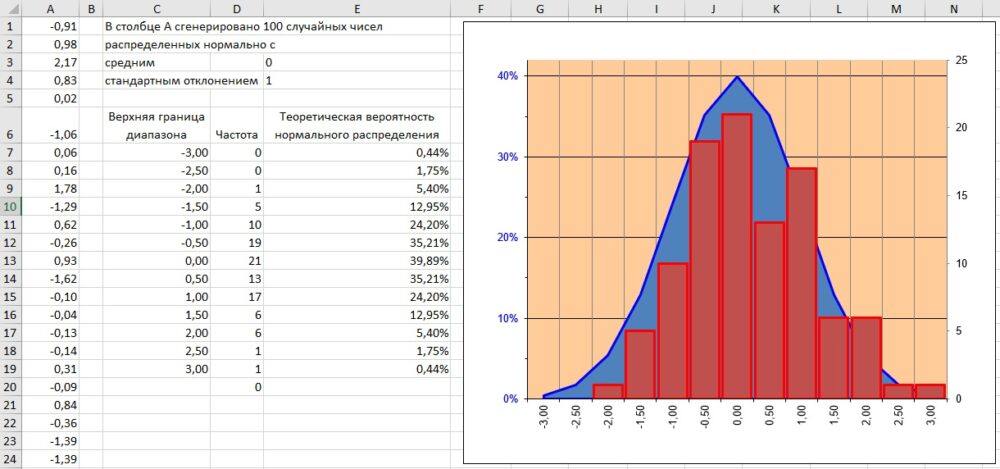
Рис. 2.3. Симуляция и теоретические вероятности нормального распределения
Что вам нужно знать. Чтобы сгенерировать 100 случайных чисел, распределенных нормально можно использовать надстройку Excel Анализ данных. Поищите эту опцию на вкладке Данные в правой части ленты. Если надстройка не установлена, пройдите по меню Файл –> Параметры, перейдите на вкладку Надстройки, и в нижней части окна в поле Управление выберите Надстройки Excel, кликните Перейти. Поставьте галочку напротив опции Пакет Анализа. Нажмите Ok.
На вкладке Данные, кликните Анализ данных и выберите опцию Генерация случайных чисел. Настройте параметры:
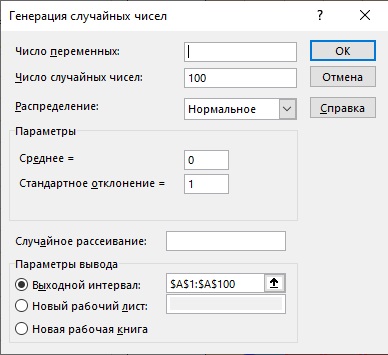
Рис. 2.4. Настройка генератора нормально распределенных случайных чисел
К сожалению, это статичный инструмент. Чтобы сгенерить новые 100 случайных чисел, нужно повторно войти в надстройку Анализ данных и запустить генератор случайных чисел. Для графика теоретической вероятности нормального распределения воспользуемся функцией Excel НОРМ.РАСП().
Что вам нужно сделать. Мы сгенерим случайные числа введя в ячейку A1 формулу: =НОРМ.ОБР(СЛМАССИВ(100;;0;1;ЛОЖЬ);E3;E4). Эта формула массива вернет 100 случайных в одном столбце, распределенные нормально со средним 0 (ячейка Е3) и стандартным отклонением 1 (Е4). Такой массив является волатильным и будет пересчитываться при каждом нажатии Shift+F9.
В ячейке С7 задайте диапазоны агрегирования случайных значений: =ПОСЛЕД(13;;E3-3*E4;E4/2). Эта функция динамических массивов вернет 13 значений, начинающихся с трех сигм меньше среднего (E3-3*E4) с шагом в половину сигмы (Е4/2). В ячейке D7 введите: =ЧАСТОТА(A1#;C7#). Первый аргумент функции ЧАСТОТА() имеет синтаксис A1#. Такого рода ссылка означает обращение ко всему динамическому массиву, заданному формулой в ячейке А1.
В ячейку Е7: =НОРМ.РАСП(C7#;E3;E4;ЛОЖЬ). Эта стандартная функция Excel также использует свойство динамических массивов. Функция в первом аргументе ожидает одно значение, а мы «подсунули» массив С7#. Поэтому функция НОРМ.РАСП() вернет не одно значение, а «разольется» по столбцу на размер массива С7#.
Понажимайте Shift+F9 и следите за изменением столбчатой диаграммы. Линейный график, отражающий теоретические значения распределения нормальной случайной величины, остается неизменным.
Глава 15. Доверительный интервал
Что делает симуляция. Модель показывает, что для генеральной совокупности со средним значением μ = 4,5 (ячейка B1) и стандартным отклонением σ = 0,7 (B2), делая выборку размером n = 35 (B3), мы на 95% (В4) можем быть уверены, что среднее значение по выборке ![]() будет между 4,27 и 4,73. Доверительный интервал (B6) будет иным, если мы изменим степень уверенности (95%). Принимая степень уверенности 95%, мы также принимаем вероятность ошибки α = 5% (B5).
будет между 4,27 и 4,73. Доверительный интервал (B6) будет иным, если мы изменим степень уверенности (95%). Принимая степень уверенности 95%, мы также принимаем вероятность ошибки α = 5% (B5).
Затем в Таблице данных с двумя переменными показано, как изменяется доверительный интервал при изменении стандартного отклонения генеральной совокупности σ и размера выборки n. Это случай анализа "что, если", основанный на вводе фиксированных значений. Поскольку симуляция изучает теоретические значения, формулы не пересчитываются при нажатии Shift+F9.
Что вам нужно знать. Ячейка B6 используется функция =ДОВЕРИТ.НОРМ(B5;B2;B3). Она имеет 3 аргумента: α = 5% (В5), σ = 0,7 (В2), n = 35 (В3). Функция возвращает величину доверительного интервала, которую следует отложить по обе стороны от среднего значения μ.

Рис. 2.5. Доверительный интервал
В отличие от предыдущих симуляций, здесь Таблица данных основана на двух переменных. Формула, на которой основаны расчеты расположена в левой угловой ячейке таблицы (В7). В ячейках С7:G7 показаны различные n, а в ячейках В8:В16 – различные σ.
Что вам нужно сделать. В ячейку B6 введите формулу: =ДОВЕРИТ.НОРМ(B5;B2;B3). В ячейку В7: =B6. Выделите диапазон. B7:G16. Пройдите по меню Данные –> Анализ "что, если" –> Таблица данных. В поле Подставлять значения по столбцам в: введите В3, а в поле Подставлять значения по строкам в: введите В2. Чтобы не ошибиться запомните правило. Когда в окне Таблицы данных предлагается Подставлять значения по столбцам в, используйте ссылку на исходное значение того параметра, которое будет в заголовках столбцов. Нажмите Ok. Это создаст в диапазоне С8:G16 формулу массива: {=ТАБЛИЦА(B3;B2)}.
Обратите внимание, что формула массива как бы связала все ячейки внутри таблицы (С8:G16). Вы не можете удалить или изменять никакую отдельную ячейку. Для изменения/удаления сначала выделите массив целиком.
Поскольку Таблица данных использует несколько значений σ и n, она не реагирует на изменения в ячейках В2 и В3. Так как среднее значение μ не используется в формулах, то изменения в В1 также не влияют на Таблицу данных. Единственным параметром, влияющим на Таблицу данных, является Степень уверенности. Чем она больше, тем больше доверительный интервал.
Глава 16. Статистическая мощность
Что делает симуляция. Модель позволяет оценить влияние ошибки I рода α (в ячейке B2 на рис. 2.6) на величину ошибки II рода β и статистическую мощность, равную 1 – β. Мощность означает вероятность выявить отличие среднего по выборке от среднего по генеральной совокупности. Или, другими словами, с некоторой степенью уверенности сказать , происходит ли выборка из генеральной совокупности, или нет. В этой модели расчеты основаны на стандартном нормальном распределении и z-значении.

Использование z-значения упрощает анализ физических кривых нормального распределения, сводя их разнообразие к стандартному виду. z-значения фактически являются единицами стандартного отклонения при среднем, равном нулю. Например, критическое значение z = 1,96 связано с ошибки 2,5% на одном конце кривой и 2,5% на другом. Т.е., при общей степени уверенности 95%.
Что вам нужно знать. Ошибка I рода описывается ситуацией, когда мы на основе выборочного исследования признали монету нечестной, хотя на самом деле она была честной (в диапазоне H24:Q24 на рис. 2.6 всего две решки и восемь орлов). Чтобы сократить вероятность ошибки I рода уменьшите α. Ошибка типа II представляет собой ситуацию, когда монета была на самом деле нечестной, но у вас было недостаточно данных, чтобы «поймать» ее (в диапазоне H26:Q6 орлов и решек поровну, хотя монета нечестная). Отличия мы объясняем простой случайностью. Чтобы снизить вероятность ошибки II рода, увеличьте размер выборки n.
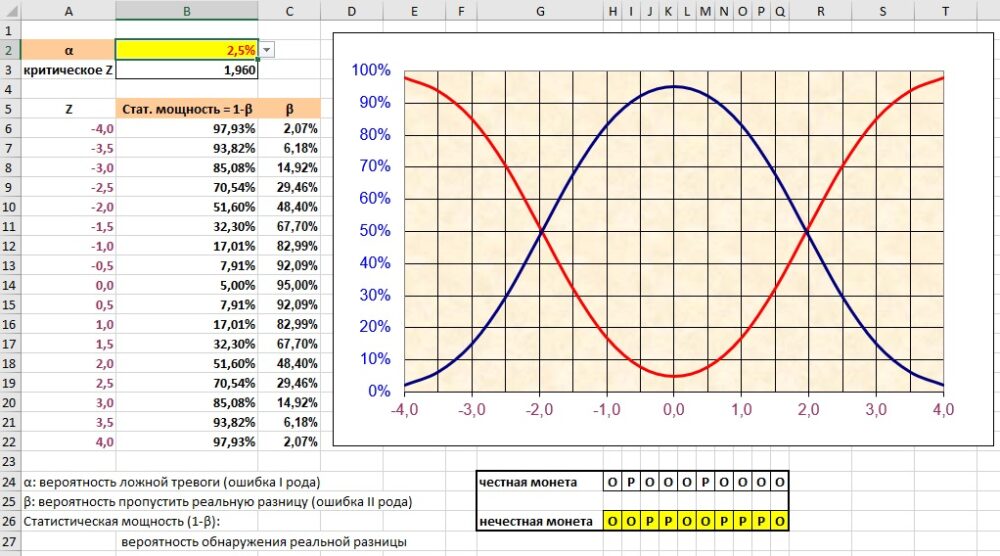
Рис. 2.6. Бета и статистическая мощность при α = 2,5%
В ячейке B3 формула =ABS(НОРМ.СТ.ОБР(B2)) возвращает значение z для вероятности, выбранной в B2. Значение z для α=2,5% равно –1,96. Минус, потому что значение вероятности маленькое, т.е. точка находится слева от пика колоколообразной кривой. Левее нуля. В правой части кривой z-значение +1,96 будет соответствовать вероятности 97,5%.
Обратите внимание на часть СТ внутри функции НОРМ.СТ.ОБР(). Это говорит о том, что функция относится к стандартному нормальному распределению с μ=0 и σ=1.
Что вам нужно сделать. Выделите ячейку B2, и пройдите по меню Данные –> Работа с данными –> Проверка данных –> Проверка данных. Настройке проверку значений:

Рис. 2.7. Проверка значений в ячейке ввода α
В ячейке B3 введите: =ABS(НОРМ.СТ.ОБР(B2)). Благодаря функции ABS критическое z-значение в ячейке В3 всегда будет положительным.
В ячейку А6 введите формулу динамического массива, задающую интервалы σ: =ПОСЛЕД(17;;-4;0,5). В ячейку С6 введите формулу ошибки II рода β: =(НОРМ.СТ.РАСП(A6#+B3;ИСТИНА)-НОРМ.СТ.РАСП(A6#-B3;ИСТИНА)). В ячейке B6: =1-C6#.
Тема взаимной зависимости ошибки I рода, ошибки II рода и статистической мощности мне представляется весьма интересной. У меня родилась идея, как иначе организовать симуляцию. Реализую и опубликую ее в ближайшее время. – Здесь и далее текст, набранный с отступом, прим. Багузина.
H24:Q24 имитирует честную монету. Введите в Н24: =ЕСЛИ(СЛМАССИВ(;10;0;1;ЛОЖЬ)>0,5;"О";"Р"). H26:Q26 – для нечестной монеты. В Н26 введите: =ЕСЛИ(СЛМАССИВ(;10;0;1;ЛОЖЬ)>0,3;"О";"Р"). Обратите внимание, честная монета выпадет орлом и решкой 50:50, а нечестная – 30 орлов против 70 решек.
Добавьте условное форматирование для честной монеты, которая 9 или 10 раз выпала одной стороной. Для диапазона H24:Q24: =ИЛИ(СЧЁТЕСЛИ($H$24:$Q$24;"О")>=9;СЧЁТЕСЛИ($H$24:$Q$24;»О»)<=1). А также подсветите нечестную монеты, если орлов ровно пять. Для диапазона H26:Q26: =СЧЁТЕСЛИ($H$26:$Q$26;"О")=5.
Увеличьте α до 10%.

Рис. 2.8. Бета и статистическая мощность при α = 10%
Здесь синяя кривая – величина ошибки II рода β, красная кривая – статистическая мощность (1–β). Если сравнить с рис. 2.6, для которого α = 2,5%, видно, что статистическая мощность увеличилась, т.е., шанс обнаружить реальные различия вырос.
Глава 17. Скрытые пики
Что делает симуляция. В модели мы имеем дело с популяцией, состоящей из двух подгрупп. Пока две субпопуляции имеют одинаковое среднее значение, даже с разными стандартными отклонениями, кривая для всей популяции будет симметричной. Но когда среднее значение одной субпопуляции меняется, кривая теряет симметрию. Вы можете смоделировать это, изменив значения в G2 и G3.
Что вам нужно знать. Популяции обычно включают скрытые подгруппы, которые могут оказать огромное влияние на состав всего населения. Как только кривая популяции теряет симметрию, стандартные статистические процедуры перестают работать. Проверка симметрии кривой может быть выполнена с помощью функции Excel СКОС(). Положительная асимметрия указывает на распределение с хвостом справа от среднего значения. Отрицательная асимметрия указывает на распределение с хвостом слева от среднего значения. Эмпирическое правило гласит, что существенной считается асимметрия меньше –1 или больше +1. Симметрия кривой является важным условием для многих статистических тестов, таких как t-критерий Стьюдента и дисперсионный анализ (ANOVA).
Что вам нужно сделать. В ячейках G2 и G3 с помощью Проверки данных установлен ограниченный набор значений. В ячейке А6 задайте 19 значений от нуля с шагом 10: =ПОСЛЕД(19;;0;10). В ячейке C6: =НОРМ.РАСП(A6#;D2;D3;ЛОЖЬ). D6: =C6#*1000. F6: =НОРМ.РАСП(A6#;G2;G3;ЛОЖЬ). G6: =F6#*1000. I6: =D6#+G6#.
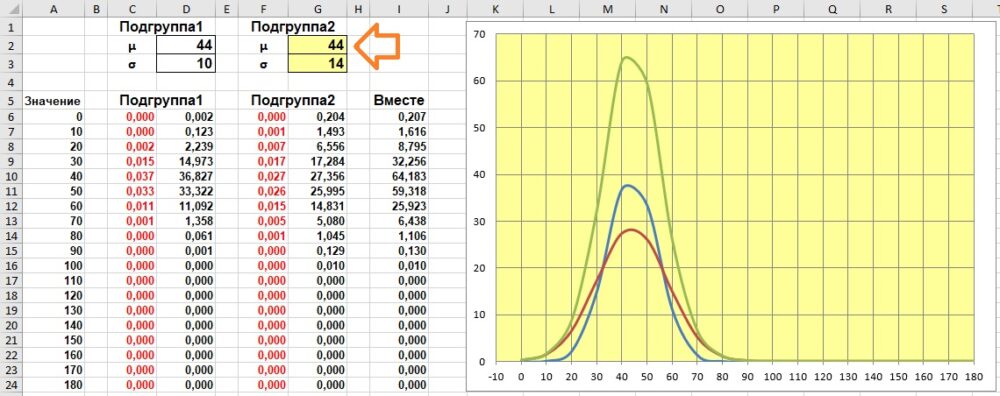
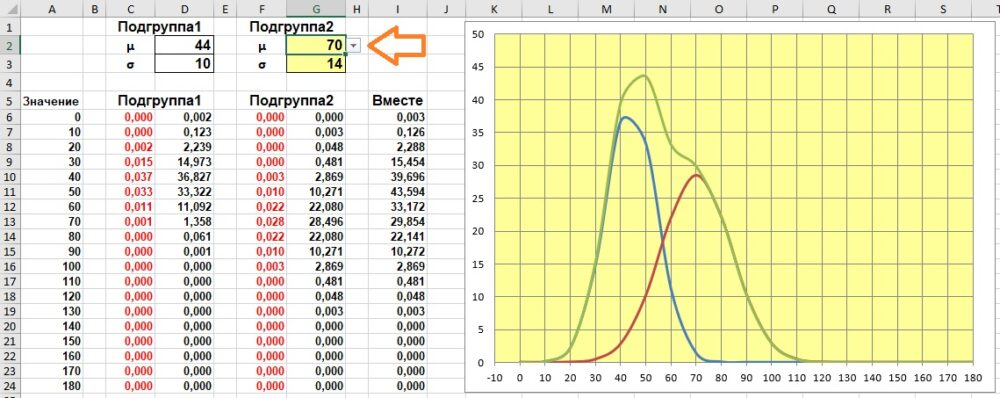
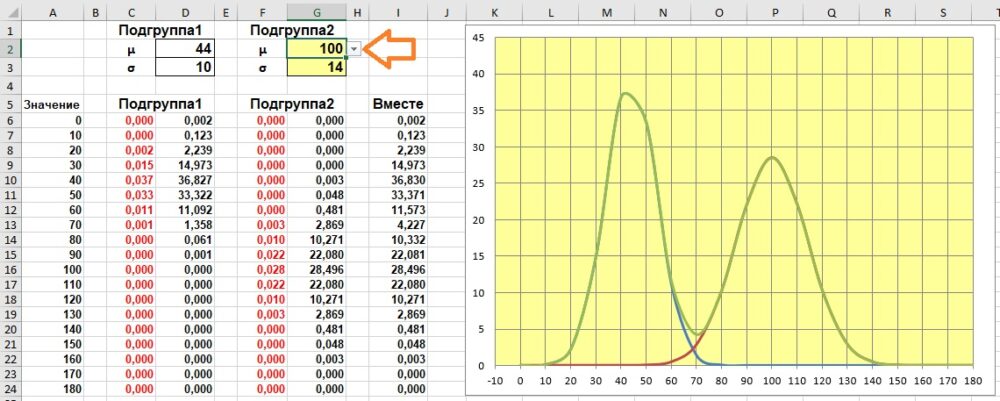
Рис. 2.9. С увеличением среднего значения второй подгруппы асимметрия всей популяции возрастает: а) μ2=44, б) μ2=70, в) μ2=100
Пройдитесь по всем доступным значениям среднего значения субпопуляции2: от 44 до 100 (G2). А также посмотрите, как отражается на графике изменение стандартного отклонения (G3).
Глава 18. Расчет размера выборки
Что делает симуляция. В популяции с неким параметром, имеющим средне значение μ (ячейка B1) и стандартное отклонение σ (B2), использовалось лечение. Делая выборку, мы хотим определить, привело ли лечение к заметным отличиям или нет. Размер отличия он же погрешность он же эффект от лечения – в ячейке В3. Минимальный размер выборки для наблюдения эффекта от лечения с уровнем достоверности 95% рассчитывается по формуле:

Что вам нужно знать. Минимальный размер выборки рассчитывается в ячейке B8. В ячейке E5 он продублирован для использования в Таблице данных. Последняя построена по двум параметрам. Столбцы используют различные отношения погрешности (эффекта) к μ, строки – вариация соотношений σ/μ.
Изменение уровня достоверности (B7) приводит к вычислению новых критических размеров выборок в Таблице данных.
Что вам нужно сделать. В ячейке B5 введите: =B2/B1. B6: =B3/B1. B8: =B5^2*(НОРМ.СТ.ОБР(1-(1-B7)/2)/B6)^2. Значение 1,96 – критическое z-значение для уровня достоверности 95%. Помните, что уровень достоверности 95% оставляет два хвоста по 2,5%, поэтому для вычисления z-значения следует использовать формулу =НОРМ.СТ.ОБР(97,5%).

Рис. 2.10. Минимальный размер выборки для обнаружения эффекта лечения
Ячейка E5: =B8. Выделите диапазон E5:K18. Пройдите по меню Данные –> Анализ "что, если" –> Таблица данных. В поле Подставлять значения по столбцам в: введите В6, а в поле Подставлять значения по строкам в: введите В5. В диапазоне F6:K18 отражается формула массива: {=ТАБЛИЦА(B6;B5)}. Скройте результаты в диапазонах F6:K6 и F7:F18, выделив их белым шрифтом. Эти результаты не представляют интереса.
В таблице добавлено условное форматирование. Красным выделены ячейки со значениями, использованными для построения Таблицы данных (из ячеек В5, В6 и В8). Горизонтальная ось (диапазон $G$5:$K$5): =И($B$6>F$5;$B$6<=G$5). Вертикальная ось (диапазон $E$7:$E$18): =И($B$5>$E6;$B$5<=$E7). Ячейки таблицы (диапазон $G$7:$K$18): =И(И($B$5>$E6;$B$5<=$E7);И($B$6>F$5;$B$6<=G$5)).
Измените уровень достоверности (B7) сначала на 99%, а затем на 90%. Критические размеры выборок в Таблице данных обновятся. Чем выше уровень достоверности мы хотим получить, тем больший размер выборки требуются. Также обратите внимание: чем меньший эффект от лечения мы хотим обнаружить, и чем больше вариабельность в выборке (σ), тем больший размер выборки нужно взять.
Глава 19. Контроль качества
Что делает симуляция. Моделирует работу сборочной линии. Объем партии может изменяться в широком диапазоне. Например, от 100 до 1000 штук (ячейка B1). Номинальное значение μ=15 (B2) подвержено изменчивости σ=2 (B3). Конкретные значения для изделий представлен в столбце А на основе генератора случайных чисел. Для обеспечения качества мы отбираем образцы (процент в E1). Если среди отобранных образцов мене 2% дефектов (E2), мы с уверенностью 95% (E3) принимаем партию. Если процент дефектов больше, мы не принимаем всю партию.
Поскольку такой процесс контроля качества сильно зависит от вероятностей, мы повторяем его несколько раз в Таблице данных.
Что вам нужно знать. Данные о партии в столбце A сформированы на основе формулы, поддерживающей динамические массивы. Число строк задается размером партии (В1). Для определения наибольшего количества дефектных деталей, которые позволяют не отбраковывать всю партию, используется функция БИНОМ.ОБР().
Что вам нужно сделать. Введите в ячейку A8 формулу динамического массива: =НОРМ.ОБР(СЛМАССИВ(B1;;0;1;ЛОЖЬ);B2;B3). Формула возвращает случайные значения в количестве из В1, распределенные нормально со средним из В2 и стандартным отклонением из В3. A6: =СРЗНАЧ(A8#).
В столбце D мы «отбираем» образцы для контроля качества. Доля отобранных образцов в Е1. Это случайный процесс, поэтому количество образцов может быть как меньше 10%, так и больше. Введите в D8: =ЕСЛИ((СЛМАССИВ(B1;;0;1;ЛОЖЬ)<E1);A8#;""). Эта формула проверяет является ли случайное значение в диапазоне от 0 до 1 меньше размера выборки (Е1). Если да, то возвращает соответствующее значение из столбца А (используя неявное пересечение). Если нет, возвращает пустое значение "".
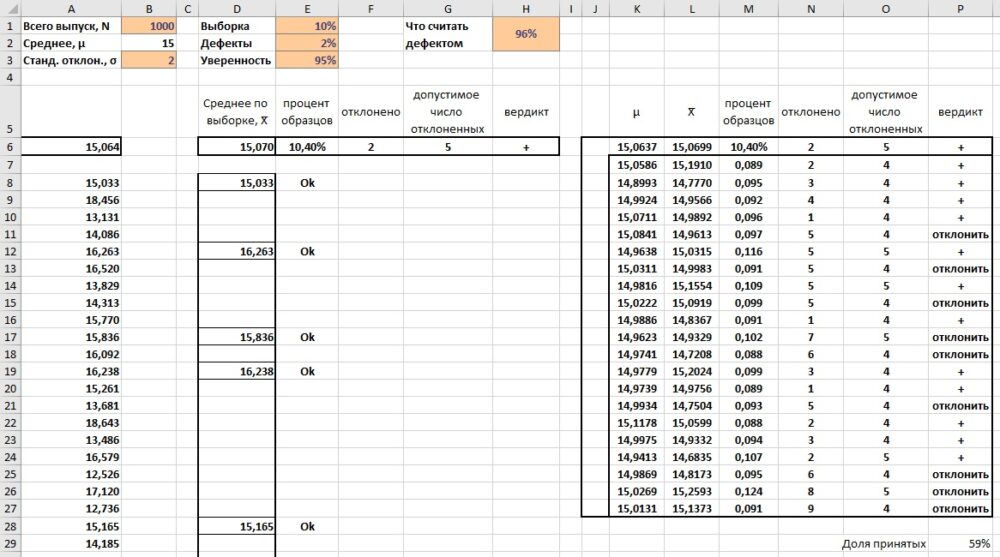
Рис. 2.11. Контроль качества
В столбце Е, начиная с ячейки Е8, мы решаем, является ли образец бракованным или нет. Введите в Е8: =ЕСЛИ(D8#<>"";ЕСЛИ((ABS(B2-D8#)/B3)>НОРМ.СТ.ОБР((1+Н1)/2);"отклонить";"Ok");""). Вероятность в Н1 подразумевает, что образцы признаются годными, если отличаются от номинального значения не более, чем на 2,054σ. Для μ=15 и σ=2 годные образцы попадают в диапазон 10,89–19,11.
В ячейках D6:H6 мы анализируем данные по выборке образцов. В D6 находим среднее по выборке: =СРЗНАЧ(D8#). В E6 проверяем, какая доля образцов была отобрана: =СЧЁТЕСЛИ(D8#;">0")/B1. В F6, сколько образцов забраковано: =СЧЁТЕСЛИ(E8#;"отклонить"). В G6 – каким может быть предельное число забракованных образцов по условиям задачи: =БИНОМ.ОБР(СЧЁТЕСЛИ(D8#;">0");E2;E3). В Н6 решаем принять или отклонить всю партию: =ЕСЛИ(F6>G6;"отклонить";"+").
Далее мы создаем шаблон для Таблицы данных. Мы ссылаемся из диапазона К6:Р6 на ячейки А6 и D6:H6. Выберите диапазон J6:P27. Пройдите по меню Данные –> Анализ "что, если" –> Таблица данных. Поле Подставлять значения по столбцам в: оставьте пустым, а в поле Подставлять значения по строкам в: кликните на любую пустую ячейку, например, R7. В диапазоне К7:Р27 появятся формулы массива: {=ТАБЛИЦА(;R7)}.
Теперь вы можете «поиграть» значениями в ячейках, выделенными на листе светло коричневым цветом.
Продолжение следует