Я часто сталкиваюсь с ситуацией, когда интересные научные концепции не используются на практике из-за сложности их представления. Одним из таких понятий является Центральная предельная теорема. Вот, что сказано в Википедии:
Центральные предельные теоремы – класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Звучит абстрактно… по крайней мере для меня. Переформулирую:
Центральная предельная теорема: независимо от формы распределения случайной величины средние выборок достаточного размера распределены нормально.
Если и эта формулировка мало что вам прояснила, не отчаивайтесь, изучите два примера.
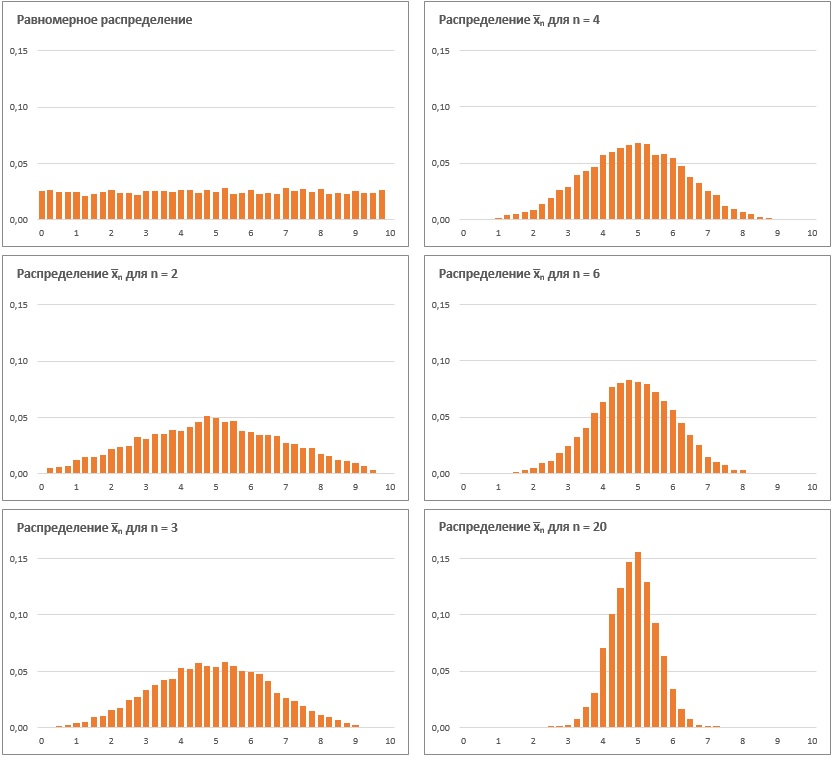
Рис. 1. Равномерное распределение случайной величины и распределение средних значений выборок разного размера
Скачать заметку в формате Word или pdf, примеры в формате Excel
Начнем с равномерного распределения (рис. 1). Я задал массив из 10 000 случайных чисел, равномерно распределенных на отрезке (0;10). Далее я подсчитал среднее значение двух случайных величин распределенных равномерно (n = 2). И таких средних я взял тоже 10 000. Видно, что распределение х̅2 уже далеко от равномерного, похоже на треугольник. По мере увеличения n распределение средних значений выборок х̅n всё более становится похожим на нормальное.
В качестве второго примера я выбрал экспоненциальное распределение ех, где х – случайное число в диапазоне 0–2,3. Такой выбор значений х связан исключительно с тем, чтобы ех имели приблизительно те же значения, что и в примере 1, т.е. от 0 до 10.
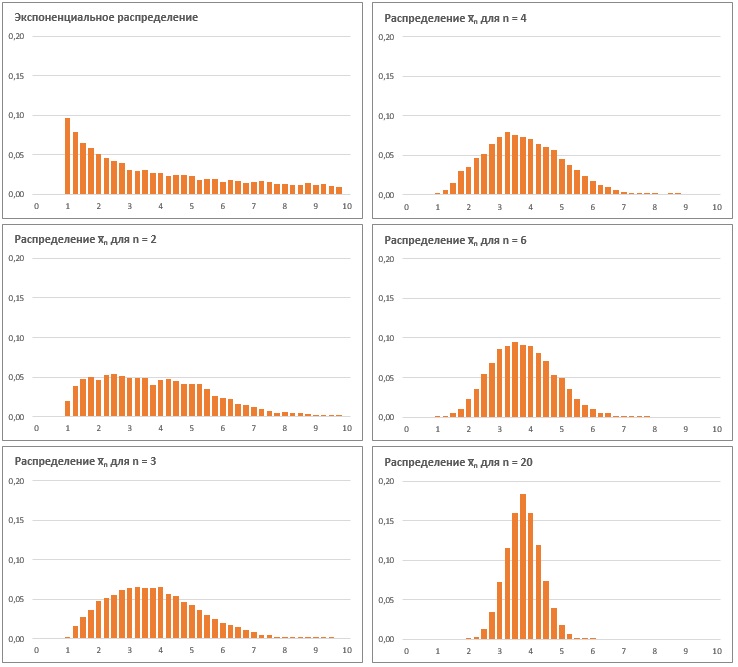
Рис. 2. Экспоненциальное распределение случайной величины и распределение средних значений выборок разного размера
Видно, что для n = 20 распределение средних значений выборок подчиняется нормальному закону. Итак
Независимо от формы распределения случайной величины средние выборок достаточного размера распределены нормально.
Надеюсь, что сейчас эта формулировка стала вам более понятной, и вы сможете использовать центральную предельную теорему на практике.
Это означает, что даже не зная какому закону отвечает распределение исследуемой вами случайной величины, вы можете взять выборку, включающую более 20 значений, и успешно применять к ней всё что вы знаете о нормально распределенных величинах. Рассчитать доверительный интервал полученного среднего значения, применить процедуру статистического вывода и т.п.
В следующей заметке я опишу любопытный метод статистического исследования, основанный на центральной предельной теореме.