Многие формы восприятия и действий можно математически смоделировать с помощью вероятностного (байесовского) вывода – метода, используемого для получения выводов на основе неопределенных данных. Согласно этим моделям, сталкиваясь с зашумленными и неоднозначными данными, человеческий мозг ведет себя как талантливый специалист по обработке данных или следователь на месте преступления. Данная богатая примерами и иллюстрациями книга представляет собой введение в методологию построения и использования вероятностных моделей перцептивного принятия решений и действий.
Вэй Цзи Ма, Конрад Кёрдинг, Дэниел Голдрайх. Байесовские модели восприятия и действия. – М.: ДМК Пресс, 2023. – 458 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 2% от объема книги), примеры в формате Excel
Глава 1. Неопределенность и вывод
Восприятие по своей сути является вероятностным и как таковое оптимально характеризуется как процесс байесовского вывода:
- условные вероятности, такие как p(A|B), представляют вероятность A при заданном B. В байесовском выводе о восприятии A и B обычно представляют состояние мира и наблюдение;
- функция правдоподобия р(наблюдение|состояние мира) отражает информационное содержание сенсорного наблюдения, относящееся к различению одного состояния мира от другого;
- чем более плоской является функция правдоподобия, тем меньше полезной информации мы получаем от наших органов чувств. Если функция правдоподобия совершенно плоская, то наблюдатель ничему не научился из наблюдения;
- априорное распределение вероятностей по состояниям мира р(состояние мира) суммирует информационное содержание наших прошлых наблюдений, т. е. исходные знания, которые у нас есть о мире. Восприятие основано не только на сенсорных наблюдениях, но и на ожиданиях, основанных на предыдущем опыте;
- более плоские априорные распределения означают, что мы меньше знаем о потенциальных состояниях мира;
- согласно правилу Байеса, апостериорная вероятность каждого гипотетического состояния мира р(состояние мира|наблюдение) вычисляется, исходя из вероятностей и априорных знаний о состояниях мира;
- восприятие, будь то зрение, слух или другие чувства, подвержены неопределенности.
Задача 1.9. Исследовательская статья под названием «Пасхальный кролик в октябре: он маскируется под утку?» поясняет, что «о внешнем виде пасхального кролика в его нерабочие дни известно очень мало». В ходе исследования авторы показали «неоднозначный рисунок утки/кролика (без указания авторства из номера Fliegende Blatter от 23 октября 1892 г.) 265 испытуемым в пасхальное воскресенье и 276 испытуемым в воскресенье в октябре 1992 г.
Авторы сообщили: «Если на Пасху рисунок значительно чаще распознавался как кролик, то в октябре большинство испытуемых считали его птицей». Рисунок, показанный авторами в своем исследовании, был похож на следующий:

Рис. 1. Кролик или утка?
Дайте байесовское объяснение результатов, полученных авторами.
Глава 2. Применение правила Байеса
Предположим, что, по нашему опыту, 10% всех полов мокрые: р(мокрый) = 0,1; р(сухой) = 0,9. Вероятности появления при отсутствии каких-либо наблюдений будут называться базовыми частотностями (base rate) в статистике или встречаемостями (prevalences) в медицине.
Порождающая модель также определяет вероятности наблюдений, обусловленных состояниями мира. Предположим, что, по нашему опыту, блестят 80% мокрых полов и только 40% сухих. Эти вероятности являются условными и принимают форму р(наблюдение|состояние мира). Эти вероятности должны быть определены для каждой комбинации наблюдения и состояния мира. Предположим, что
р(блестящий|мокрый) = 0.8
р(неблестящий|мокрый) = 0.2
р(блестящий|сухой) = 0.4
р(неблестящий|сухой) = 0.6
Вывод можно сделать, используя правило Байеса
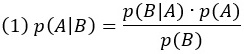
где А и В – любые две случайные величины.
В контексте вывода А – это скорее гипотетическое, чем фактическое состояние мира, и мы часто будем обозначать его через Н (от англ. hypothesized – гипотетический, предполагаемый). B – это наблюдение или набор наблюдений, которые мы будем обозначать как «obs» (от англ. observation – наблюдение).
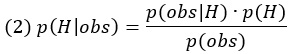
Здесь p(H) называется априорной вероятностью H, p(obs|H) называется правдоподобием H, а p(H|obs) – апостериорной вероятностью H. Это уравнение отражает интуитивно понятный характер правила Байеса применительно к оценке гипотез: если гипотеза чаще оказывается верной в мире, то еще до того, как мы примем во внимание наблюдения, эта гипотеза является более вероятной (априорность), и если наблюдения более ожидаемы при гипотезе (правдоподобие), то эта гипотеза также более вероятна.
Не говорите «правдоподобие наблюдения». Правдоподобие всегда является функцией гипотетического состояния мира. Оно равно вероятности данного наблюдения при гипотетическом состоянии мира.
Числитель в правиле Байеса – произведение правдоподобия и априорной вероятности – не имеет официального названия, но мы будем называть его протопостериором гипотезы H:
Protoposterior(H) = p(obs|H)p(H) = p(H,obs)
В нашем примере протопостериорами двух гипотез являются
Protoposterior(мокрый) = Prior(мокрый) * Likelihood(мокрый) = 0.1 * 0.8 = 0.08
Protoposterior(сухой) = Prior(сухой) • Likelihood(сухой) = 0.9 • 0.4 = 0.36
Протопостериор – это вероятность гипотезы и наблюдения вместе. В нашем примере 8% полов мокрые и блестящие, а 36% полов сухие и блестящие. Как и вероятности, протопостериорные значения в целом не будут в сумме равны 1.
Правило Байеса (2) говорит нам разделить протопостериорные значения на p(obs), вероятность наблюдений независимо от того, каким состоянием мира они были произведены. Оказывается, вероятность p(obs) равна сумме протопостериоров по всем гипотезам:

Чтобы получить апостериорные вероятности, сумма которых равна 1, мы нормализуем протопостериорные вероятности, то есть разделим каждую на их сумму p(obs). В этом смысле p(obs) является нормирующим множителем в правиле Байеса. В нашем примере
Posterior(мокрый) = р(мокрый|блестит) = Protoposterior(мокрый) / р(блестящий) = 0.08/0.44 = 0.182
Posterior(сухой) = р(сухой|блестит) = Protoposterior(сухой) / р(блестящий) = 0.36/0.44 = 0.818
Таким образом, p(obs) гарантирует, что, в отличие от правдоподобий или протопостериорных вероятностей, апостериорные вероятности всегда в сумме равны 1, то есть нормированы.
Применение (readout) апостериорного распределения – это отображение апостериорного распределения на решение или восприятие. Самый очевидный вывод – выбрать максимум, т. е. гипотезу с наибольшей апостериорной вероятностью. Этот выбор также называется максимальной апостериорной (maximum a posteriori, MAP) оценкой.
Задача 2.4. В некотором университете 15% всех студентов обучаются гуманитарным специальностям, 55% всех студентов являются студентами бакалавриата и 18% магистрантов обучаются гуманитарным специальностям. Какова вероятность того, что случайный студент-гуманитарий является магистрантом?
Глава 3. Байесовский вывод в условиях зашумленных измерений
Поскольку сигнал зашумлен, стимулу отвечает не одно значение, а вероятностное распределение. Распределение, связанное со стимулом s, обозначается как ps(s). Это распределение состояний мира или – в нашем текущем примере – распределение стимулов отражает, как часто встречается каждое возможное значение s.
Наиболее часто используемым непрерывным распределением вероятностей является распределение Гаусса, или нормальное распределение.
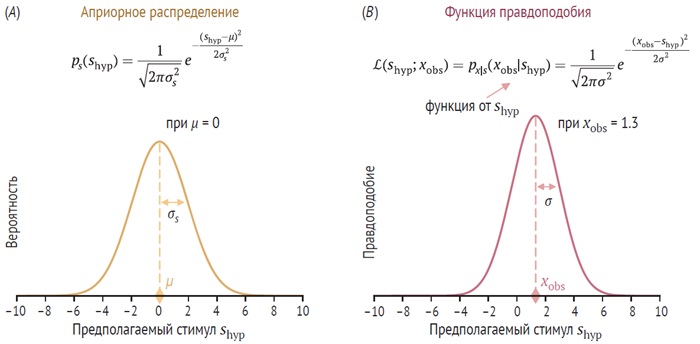
Рис. 2. Рассмотрим одно испытание, в котором измеряется xobs. Наблюдатель пытается сделать вывод, какое значение стимула s произвело это измерение. Две функции, которые играют роль в процессе вывода наблюдателя (в одном испытании), – это априорная вероятность и правдоподобие. Аргументом как априорного распределения, так и функции правдоподобия является гипотетический стимул shyp: (А) априорное распределение. Это распределение отражает убеждения наблюдателя о различных возможных значениях, которые может принимать стимул; (В) функция правдоподобия от стимула на основе измерения xobs. Функция правдоподобия сосредоточена на xobs
Используя функцию правдоподобия, можно сделать наилучшее предположение о значении стимула. Это наилучшее предположение называется оценкой максимального правдоподобия (maximum-likelihood estimate, MLE).
Апостериорное распределение
Байесовский наблюдатель вычисляет апостериорное распределение состояния мира на основе наблюдений, используя знание порождающей модели. В нашем примере апостериорное распределение представляет собой p(shyp|xobs) – функцию плотности вероятности для гипотетического стимула shyp при заданном измерении xobs. Правило Байеса принимает вид
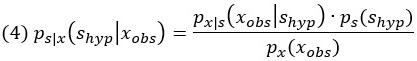
Его также часто записывают как
![]()
Это означает, что апостериорное распределение пропорционально произведению правдоподобия и априорного распределения. Это произведение мы назвали протопостериором. В последних двух выражениях мы использовали знак пропорциональности вместо множителя , поскольку этот множитель действует просто как нормировочный коэффициент. Если мы не знаем нормировочный коэффициент, мы все равно знаем полную форму апостериорного распределения вероятностей.

Рис. 3. Отношения между правдоподобием, нормированным правдоподобием, протопостериором и апостериорным распределением. Игнорирование априорного распределения равнозначно допущению того, что это распределение плоское
Итак, у нас два распределения Гаусса по одной и той же случайной величине у – априорное и правдоподобие. Одно имеет среднее μ1 и дисперсию σ1, а другое – среднее μ2 и дисперсию σ2. Произведение двух распределений Гаусса дает распределение Гаусса. Выражения, возникающие в результате умножения гауссиан, включают в себя несколько множителей σ2. Для упрощения вводят точность (precision) – величину, обратную дисперсии: J = 1/ σ2 с добавлением индексов по мере необходимости.
В этих обозначениях среднее апостериорного распределения
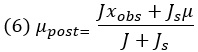
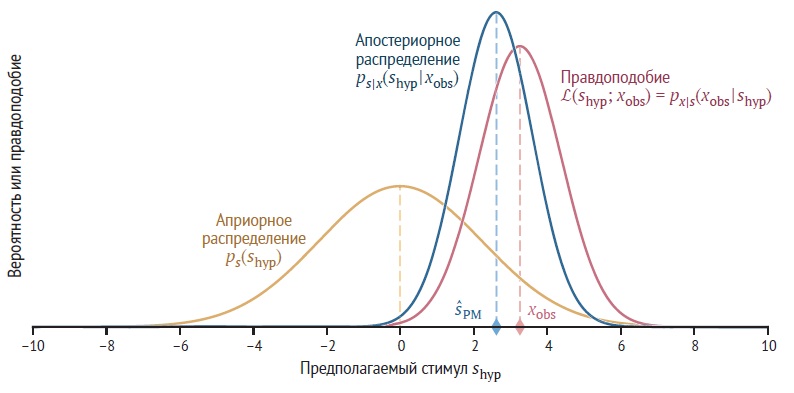
Рис. 4. Апостериорное распределение получается путем умножения априорного распределения на функцию правдоподобия и нормирования полученной функции (протопостериор). Предполагаемое значение стимула с наибольшей апостериорной вероятностью является апостериорной средней оценкой стимула наблюдателем ŝPM
Выражение среднего имеет вид
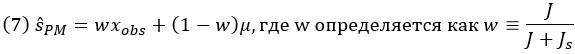
Поскольку J и Js оба неотрицательны, w представляет собой число от 0 до 1. Другими словами, апостериорное среднее представляет собой взвешенное среднее наблюдаемого измерения xobs и априорного среднего µ. Это средневзвешенное значение всегда будет находиться где-то между xobs и µ.
Где именно находится µpost, определяется весами w и 1 – w, приложенными к наблюдению и априорному среднему соответственно. Веса представляют собой нормализованные версии точности функции правдоподобия и априорного распределения. Если дисперсия правдоподобия ниже, чем у априорного распределения, точность правдоподобия (т. е. надежность измерения) выше, чем у априорного распределения. Как следствие вес для xobs выше, чем для µ, в результате чего апостериорное среднее лежит ближе к xobs, чем к µ. Конечно, верно и обратное: если дисперсия правдоподобия больше, чем априорного распределения, то апостериорное среднее будет ближе к априорному среднему, чем к измерению. По правилу Байеса априорные вероятности и правдоподобие – это всего лишь две части информации, которые необходимо объединить. Каждая часть информации имеет влияние, соответствующее качеству информации.
Неопределенность
Байесовскому выводу присуща неопределенность: априорная неопределенность отражает качество знаний наблюдателя о состоянии мира до того, как он сделает какие-либо наблюдения, неопределенность правдоподобия или сенсорная неопределенность отражают качество знаний наблюдателя о состоянии мира, основанных исключительно на наблюдениях, а апостериорная неопределенность отражает качество знаний наблюдателя о состоянии мира после проведения наблюдений.
Если все распределения являются гауссовыми, и если неопределенность представляет собой стандартное отклонение, ее значения равны: априорная неопределенность – σs; неопределенность правдоподобия ли сенсорная неопределенность – σ; апостериорная неопределенность:
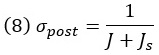
Для гауссовых априорных распределений и правдоподобий апостериорная неопределенность всегда меньше как априорной неопределенности, так и неопределенности правдоподобия.
В этой книге термин «шум» зарезервирован для процесса, посредством которого генерируются наблюдения, то есть он описывает изменчивость наблюдений или измерений от испытания к испытанию. Таким образом, шум является частью порождающей модели. «Неопределенность», с другой стороны, отражает наличие или отсутствие знаний наблюдателя в отношении переменных в мире. Ширина апостериорного распределения является мерой неопределенности, а не шума. Неопределенность является частью процесса вывода и субъективна, поскольку определяется не только наблюдением, но и априорными знаниями субъекта. Шум является одной из возможных причин неопределенности, но не единственной. Например, когда объект частично закрыт и нет прямой информации о части объекта, находящейся за мешающим предметом, наблюдатель имеет неопределенность без шума.
Гетероскедастичность
Когда дисперсия случайной величины зависит от среднего значения распределения, мы наблюдаем пример гетероскедастичности. Гетероскедастичность не мешает нам сформулировать байесовскую модель. Однако она приводит к тому, что функции правдоподобия не являются гауссовыми, даже если распределение измерений является гауссовым.
Амплитудные переменные
Переменные, которые никогда не принимают отрицательных значений, можно назвать амплитудными переменными (magnitude variable). Один из типов распределения вероятностей, предназначенных для амплитудных переменных, – это логарифмическое нормальное распределение (lognormal distribution). Поскольку область определения s равна [0, ∞), областью определения логарифма s является вся числовая прямая . Следовательно, можно определить распределение Гаусса для log s:
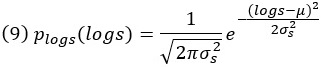
Приводя его к исходной переменной s, мы получаем
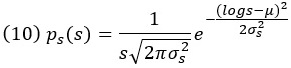
Множитель 1/s, называемый якобианом. Это логнормальное распределение с параметрами µ и σs2, также записываемое как Lognormal(s; µ, σs2). Параметры µ и σs2 не соответствуют непосредственно среднему значению и дисперсии. Среднее значение логнормально распределенной переменной s равно
![]()
Медиана s при логнормальном распределении равна eµ.
Важным свойством логнормального распределения является тот факт, что стандартное отклонение пропорционально среднему значению. Оказывается, это эмпирически правильное описание человеческих суждений о величине – соотношение, называемое законом Вебера-Фехнера. Например, уровень шума при измерении наблюдателем длины линии пропорционален самой длине.
Глава 6. Обучение как вывод
Бета-распределение определяется случайной величиной Y, которая принимает значения от 0 до 1. Чаще всего эта случайная величина сама является вероятностью, поэтому бета-распределение – это распределение вероятностей по вероятностной переменной. Плотность вероятности бета-распределения
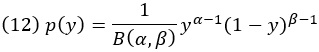
Здесь α и β – параметры распределения, причем оба должны быть положительными; B(α,β) обозначает бета-функцию – специальную функцию, роль которой (и фактически определение) заключается в нормировании бета-распределения. В Excel есть функции БЕТА.РАСП() и БЕТА.ОБР(). Несколько примеров бета-распределения:
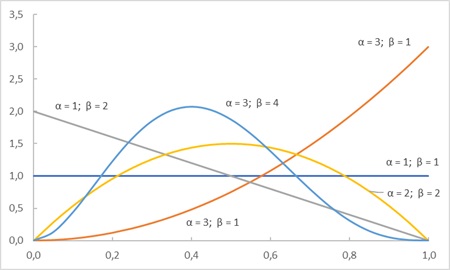
Рис. 5. Примеры бета-распределения для различных комбинаций параметров
Среднее значение бета-распределенной случайной величины y
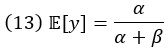
а дисперсия
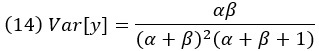
Гамма-распределение
Гамма-распределение определяется случайной величиной Y, которая принимает значения на положительной действительной числовой оси, такие как точность в нашем примере. Плотность вероятности гамма-распределения
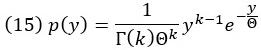
Здесь k и Θ – параметры распределения, причем оба они должны быть положительными. k называется параметром формы, а Θ – параметром масштаба. Γ(∙) обозначает гамма-функцию – специальную функцию, также представленную в Excel – ГАММА.РАСП() и ГАММА.ОБР().
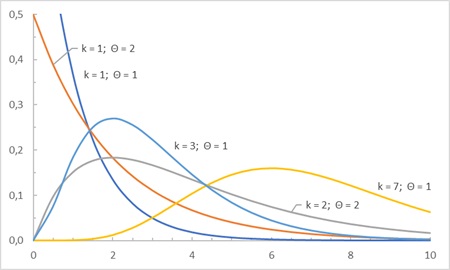
Рис. 6. Примеры гамма-распределения при различных комбинациях параметров
Среднее значение гамма-распределенной случайной величины y
![]()
Дисперсия
![]()
Глава 10. Одинаковый или разный?
Извлечение информации о структуре мира из сенсорного ввода является важной частью, если не конечной целью восприятия. Мир сильно структурирован: форма объекта состоит из цепочки мелких линейных элементов, объекты упорядочены по глубине, а музыкальное произведение состоит из точно подобранных последовательностей тонов. Как показывает знаменитая иллюзия Канижа, мозг воспринимает визуальную структуру, даже если существуют лишь косвенные сенсорные доказательства ее существования.
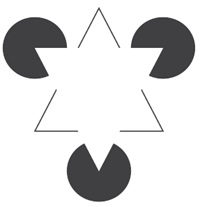
Рис. 7. Треугольник Канижа. Люди склонны видеть белый треугольник, лежащий поверх трех черных дисков
Действительно, на каком-то уровне все наше восприятие структуры основано на косвенной информации. Когда мы идем по оживленной улице, наш мозг, казалось бы, без особых усилий отделяет несколько источников звука от единого непрерывного потока. Можно утверждать, что распознавание объектов, независимо от сенсорной модальности, состоит из обнаружения структур на нескольких уровнях.
С момента зарождения психологии исследователей интересовало то, как мозг воспринимает структуру среди наборов составляющих элементов. По большей части объяснения явлений структурного восприятия были качественными и описательными. В основе этих объяснений лежат законы гештальта, или принципы гештальта, которые описывают, при каких обстоятельствах элементы воспринимаются как принадлежащие к целому (как в иллюзии Канижа). Существует длинный список таких законов:
- закон непрерывности: элементы, которые предполагают продолжение визуальной линии, обычно группируются вместе;
- закон замыкания: такие объекты, как формы, буквы, изображения и т. д., воспринимаются как цельные, даже если они не завершены (рис. 8A);
- закон подобия: элементы в ассортименте объектов перцептивно группируются вместе, если они подобны друг другу (рис. 8B);
- закон общей судьбы: объекты воспринимаются как связанные, если они указывают в одном направлении;
- закон близости: объекты, расположенные близко друг к другу, воспринимаются как образующие группу (рис. 8C-D);
- закон хорошего гештальта: объекты воспринимаются как сгруппированные вместе, если они образуют регулярный, простой и упорядоченный паттерн.
Практически с самого момента своего появления законы гештальта подвергались критике за расплывчатость, например в законе хорошего гештальта, где понятия «регулярный», «простой» и «упорядоченный» не определены. Более того, законы гештальта становятся еще более туманными, когда они противоречат друг другу. Байесовские модели могут улучшить эти законы, поскольку байесовские модели имеют нормативную основу и допускают точные количественные описания. Основная идея заключается в том, что наблюдатель рассматривает две гипотезы – например, элементы принадлежат друг другу или нет – и оценивает их апостериорные вероятности.
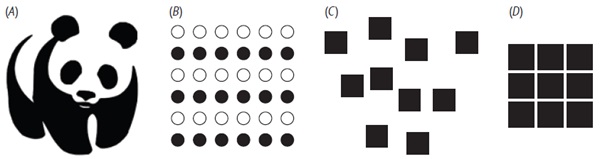
Рис. 8. (А) Закон замыкания; (В) закон подобия; (C-D) закон близости: левое множество рассматривается как девять несвязанных квадратов, а правое множество – как один квадрат
Глава 13. Сочетание вывода с полезностью
История теории полезности
Даниил Бернулли, а до него Габриэль Крамер работали над петербургским парадоксом. Этот парадокс связан с простой азартной игрой: в каждом раунде подбрасывается честная монета, и игра заканчивается, как только монета выпадает решкой (T). Затем испытуемый получает 2h долларов, где h – количество наблюдаемых орлов (H). Например, если наблюдаемая последовательность бросков монеты равна T, игрок выиграет 1 доллар; НТ – 2 доллара; ННТ – 4 доллара; HHHT – 8 долларов и т. д. Оказывается, возможный выигрыш в этой игре бесконечен. Ожидаемая полезность – это сумма всех возможных исходов выигрыша, умноженная на вероятность исхода. Представляя каждый возможный исход количеством орлов, мы имеем:
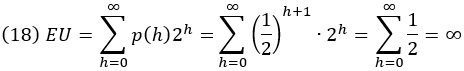
Парадокс заключается в том, что хотя ожидаемая полезность бесконечна, люди не будут платить больше нескольких долларов за участие в игре. Один из способов разрешить этот парадокс – ввести функцию полезности, отражающую убывающую предельную полезность денег: 1 001 000 долларов лишь немногим более ценны, чем 1 000 000 долларов, тогда как 1000 долларов гораздо ценнее, чем ничего.
Джереми Бентам, другой мыслитель, рассматривавший идею полезности, применил ее более непосредственно к удовольствиям и страданиям людей. Он использовал эти идеи, чтобы определить, как должно быть организовано общество, а именно путем максимизации полезности всех граждан – философии утилитаризма. Бентам считал, что все моральные и правовые нормы выводятся из этого простого принципа с использованием методов логики и эксперимента.