Владимир Гмурман. Теория вероятностей и математическая статистика

Многие поколения студентов хорошо знают это пособие, ставшее классическим учебным изданием. Его ценность заключается в том, что сложные вопросы теории вероятностей и математической статистики изложены в логической последовательности и доступной форме. Большое количество примеров позволяет лучше усвоить материал, а задачи, приведенные в конце каждой главы, – закрепить полученные знания. Мои комментарии даны с отступом.

Владимир Гмурман. Теория вероятностей и математическая статистика. – М.: Издательство Юрайт, 2023. – 480 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 10% от объема книги), примеры в формате Excel

Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon

ЧАСТЬ ПЕРВАЯ. СЛУЧАЙНЫЕ СОБЫТИЯ

Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Классическое определение. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Глава вторая. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Сумма вероятностей событий A₁, A₂, … A_n, образующих полную группу, равна единице:

Сумма вероятностей противоположных событий равна единице:

Глава третья. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Условной вероятностью Р_А(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

Для независимых событий теорема умножения (3.1) имеет вид

Вероятность появления хотя бы одного из событий A₁, A₂, … A_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий A̅₁, A̅₂, … A̅_n:

Если события A₁, A₂, … A_n имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий

Глава четвертая. СЛЕДСТВИЯ ТЕОРЕМ СЛОЖЕНИЯ И УМНОЖЕНИЯ

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Если события A и В несовместны, то их совмещение есть невозможное событие и, следовательно, Р(AВ) = 0. Формула (4.1) для несовместных событий принимает вид

Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B₁, В₂, …, В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

Вероятность гипотез. Формулы Байеса

Пусть событие A может наступить при условии появления одного из несовместных событий B₁, В₂, …, В_n, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется формуле полной вероятности (4.3).

Допустим, что произведено испытание, в результате которого появилось событие A. Поставим своей задачей определить, как изменились (в связи с тем, что событие A уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности Р_А(В₁), Р_А(В₂), …, Р_А(В_n).

Найдем сначала условную вероятность Р_А(В₁). По теореме умножения имеем

Отсюда

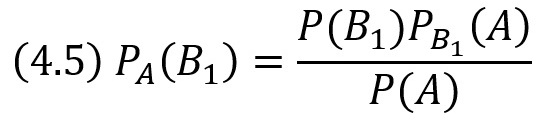
Заменив здесь Р(А) по формуле (4.3), получим

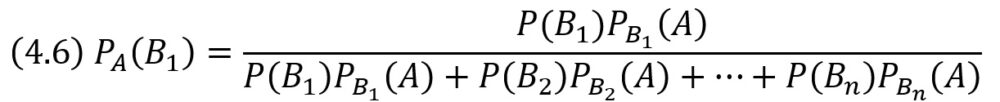
Формулы (4.5) и (4.6) называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие A.

Глава пятая. ПОВТОРЕНИЕ ИСПЫТАНИЙ

Формула Бернулли

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же – р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – p.

Вероятность того, что при n испытаниях событие А осуществится ровно k раз определяется формулой Бернулли:

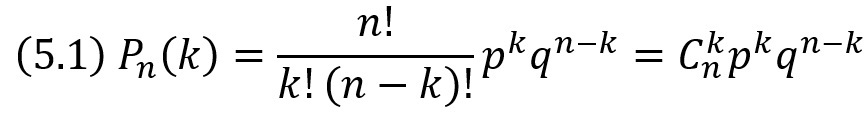
Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико. Для частного случая р = 1/2 асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему иногда называют теоремой Муавра – Лапласа.

Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции

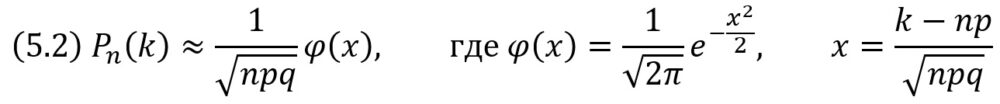
Имеются таблицы, в которых помещены значения функции φ(х) соответствующие положительным значениям аргумента х (рис. 1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция φ(х) четна, т. е. φ(–х) = φ(х).

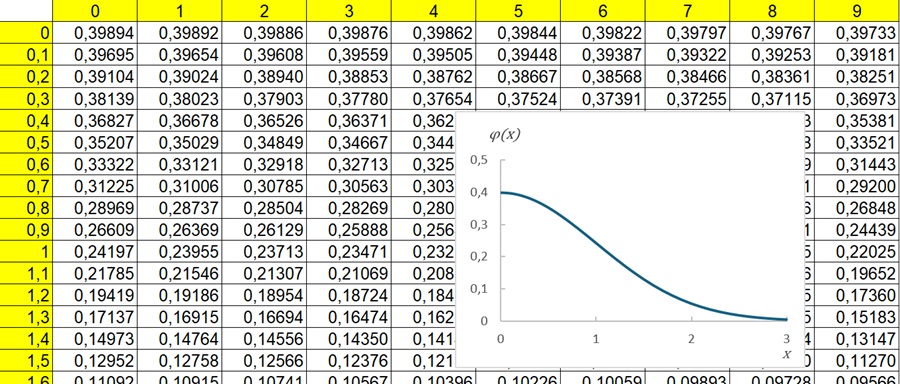
Рис. 1. Таблица значений функции Лапласа φ(х)

В Excel функции Лапласа φ(х) соответствует функция =НОРМ.СТ.РАСП(х;ЛОЖЬ).

Интегральная теорема Лапласа

Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_n(k₁,k₂) того, что событие А появится в n испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу

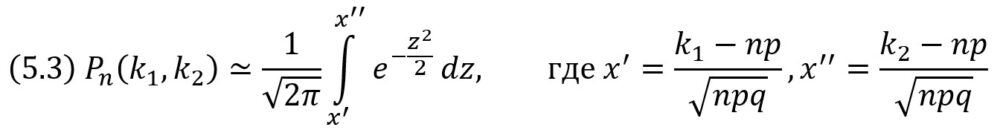
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются таблицами, так как неопределенный интеграл не выражается через элементарные функции. Таблица для интеграла

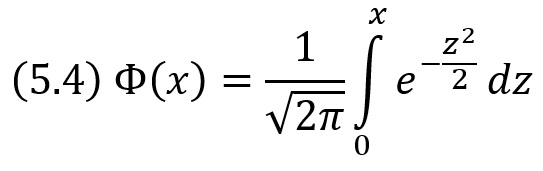
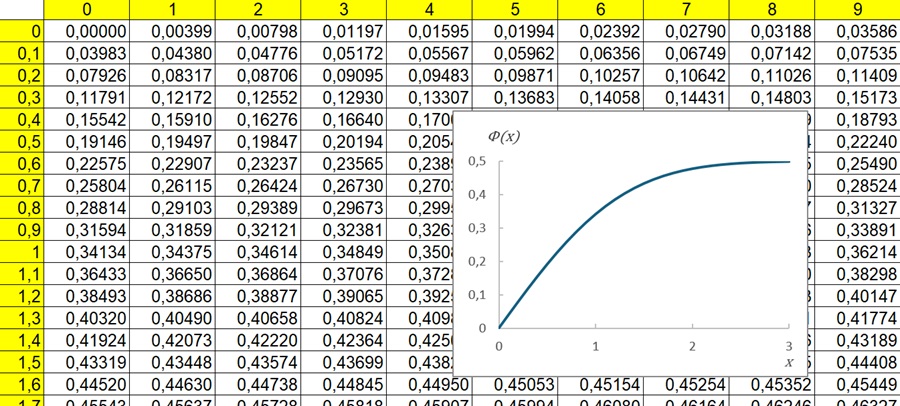
Рис. 2. Таблица значений интегральной функции Лапласа Ф(х)

В Excel интегральную функцию Лапласа Ф(х) можно найти с помощью формулы =НОРМ.СТ.РАСП(х;ИСТИНА) – 0,5.

ЧАСТЬ ВТОРАЯ. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Глава шестая. ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

X            x₁          x₂           …           х_n

Р            p₁          p₂          …           p_n

Биномиальное распределение

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q = 1 – р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения X таковы: x₁ = 0, х₂ = 1, х₃ = 2, …, х_n+1 = n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли (2.15). Эта формула является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (2.15) можно рассматривать как общий член разложения бинома Ньютона:

Таким образом, первый член разложения рⁿ определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член np^n–1q определяет вероятность наступления события n – 1 раз; …; последний член qⁿ определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

X            n             n–1         …           k                …           0

Р            npⁿ        np^n–1q   …      C_n^kp^kq^n—k     …           qⁿ

Распределение Пуассона

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р ≤ 0,1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.

Если произведение nр сохраняет постоянное значение, а именно nр = λ, то

Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0 < р < 1) и, следовательно, вероятность его непоявления q = 1 – р. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в k-м испытании, то в предшествующих k – 1 испытаниях оно не появлялось.

Обозначим через X дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями X являются натуральные числа: х₁= 1, х₂ = 2, …

Пусть в первых k – 1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

Полагая k = 1, 2, получим геометрическую прогрессию с первым членом р и знаменателем q (0 <q < 1): p, qp, q²p, … q^k–1p, …

По этой причине распределение (6.3) называют геометрическим.

Гипергеометрическое распределение

Пусть в партии из N изделий имеется М стандартных (М < N). Из партии случайно отбирают n изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима). Обозначим через X случайную величину – число m стандартных изделий среди n отобранных. Очевидно, возможные значения X таковы: 0, 1, 2, …, min (М, n).

Найдем вероятность того, что X = m, т. е. что среди n отобранных изделий ровно m стандартных.

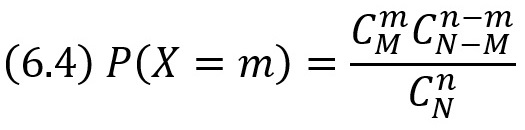
Глава седьмая. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

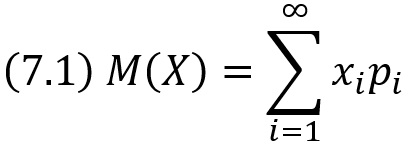
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Математическое ожидание постоянной величины равно самой постоянной:

Постоянный множитель можно выносить за знак математического ожидания:

Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

Математическое ожидание М(X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

Глава восьмая. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.

По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.

Отклонением называют разность между случайной величиной и ее математическим ожиданиям. Но, математическое ожидание отклонения равно нулю:

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:

Дисперсия постоянной величины C равна нулю:

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:

Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:

Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в  раз меньше среднего квадратического отклонения σ каждой из величин:

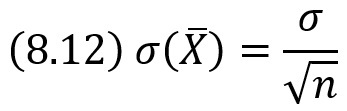
Начальные и центральные теоретические моменты

Рассмотрим дискретную случайную величину X, заданную законом распределения:

X            1           2            5           100

Р            0,6        0,2        0,19      0,01

Найдем математическое ожидание X: М(Х) = 1*0,6 + 2*0,2 + 5*0,19 +100*0,01 =2,95.

Напишем закон распределения X²:

X²          1            4            25         10 000

р            0,6        0,2        0,19      0,01

Найдем математическое ожидание X²: М(X²) = 1*0,6 + 4*0,2 + 25*0,19 + 10 000*0,01 = 106,15. Видим, что М(X²) значительно больше М(X). Это объясняется тем, что после возведения в квадрат возможное значение величины X², соответствующее значению х = 100 величины X, стало равным 10 000, т. е. значительно увеличилось; вероятность же этого значения мала (0,01).

Таким образом, переход от М(X) к М(X²) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X², а тем более к величинам X³, X⁴ и т. д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).

Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

В частности,

Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X–M(X))^k:

В частности,

Глава девятая. ЗАКОН БОЛЬШИХ ЧИСЕЛ

Неравенство Чебышева. Вероятность P того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, можно выразить неравенством:

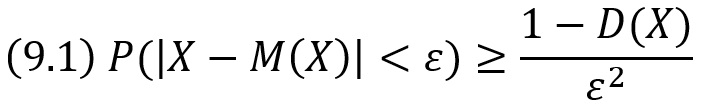
Теорема Чебышева. Если Х₁, Х₂, …, Х_n, … – попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число ε, вероятность неравенства

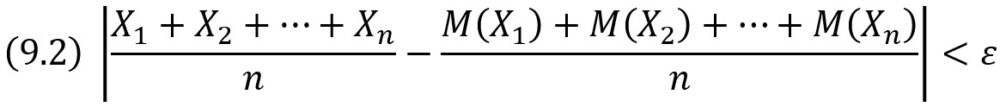
будет как угодно близка к единице, если число случайных величин достаточно велико.

Сущность теоремы Чебышева. Среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов.

Теорема Бернулли. Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если ε – сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

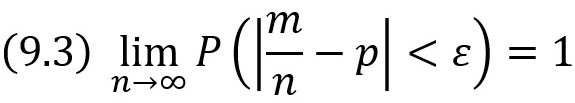
Глава десятая. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е.

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Иногда вместо термина «функция распределения» используют термин «интегральная функция».

Значения функции распределения принадлежат отрезку [0, 1]:

F(х) – неубывающая функция, т. е.

Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(х) = 0 при х ≤ а 2) F(х) = 1 при х ≥ b.

Глава одиннадцатая. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) – первую производную от функции распределения F(х):

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

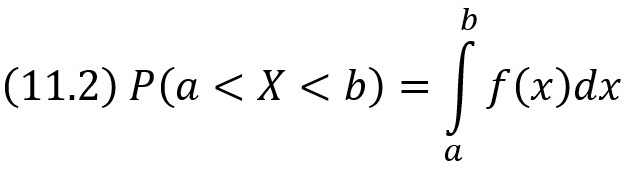
Зная плотность распределения f(х), можно найти функцию распределения F(х) по формуле

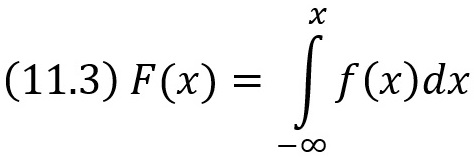
Глава двенадцатая. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

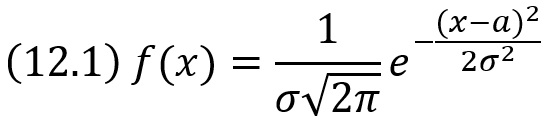
Нормальное распределение определяется двумя параметрами a и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение. Вероятностный смысл этих параметров таков: a есть математическое ожидание, σ – среднее квадратическое отклонение нормального распределения.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Исследуем функцию (12.1) методами дифференциального исчисления.

Функция определена на всей оси х. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю:

т.е. ось Ох служит горизонтальной асимптотой графика.

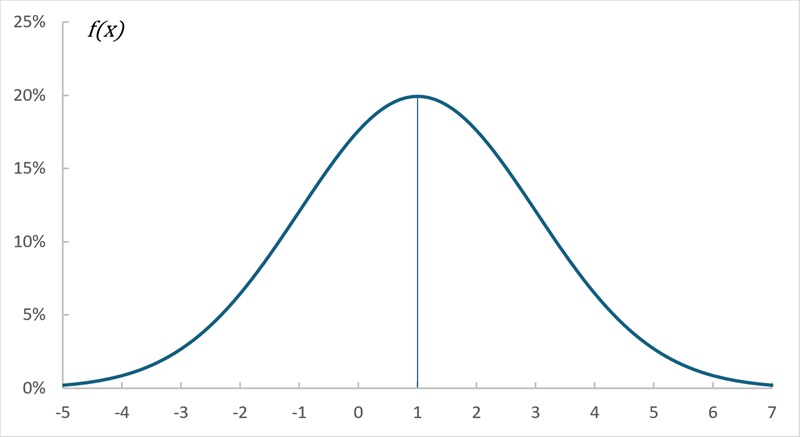
Рис. 3. Нормальная кривая при a = 1 и σ = 2

Исследуем функцию на экстремум. Найдем первую производную:

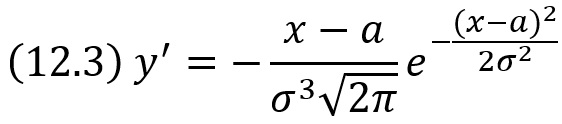
у’ = 0 при х = а, у’ > 0 при х < а, у’ < 0 при х > а.

Следовательно, при х = а функция имеет максимум, равный:

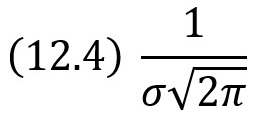
Разность х – а содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х – а.

Исследуем функцию на точки перегиба. Найдем вторую производную:

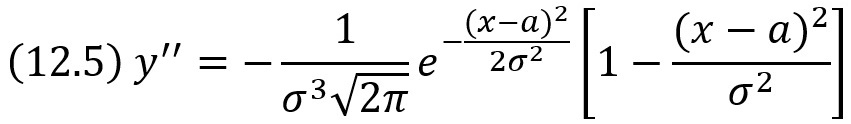
Легко видеть, что при x = a + σ и х = а – σ вторая производная равна нулю, а при переходе через эти точки она меняет знак. В обеих этих точках значение функции равно:

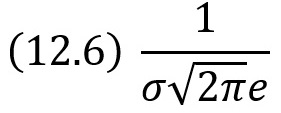
Таким образом, точки графика

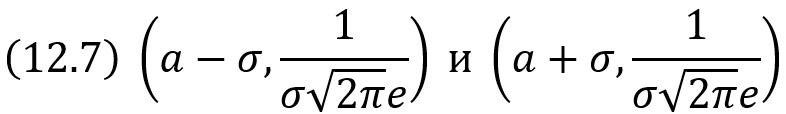
являются точками перегиба.

Формулировка центральной предельной теоремы

Известно, что нормально распределенные случайные величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А. М. Ляпуновым (центральная предельная теорема): если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

Характеристической функцией случайной величины X называют функцию

Для дискретной случайной величины X с возможными значениями х_k и их вероятностями p_k характеристическая функция

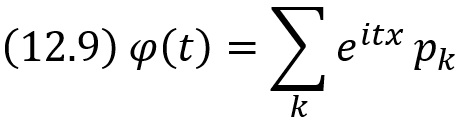
Для непрерывной случайной величины X с плотностью распределения f(х) характеристическая функция

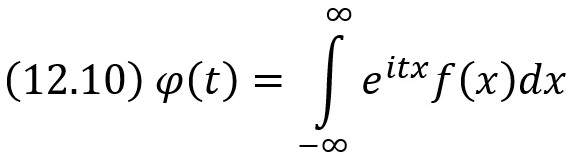
Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс

Эмпирическим называют распределение относительных частот. Эмпирические распределения изучает математическая статистика.

Теоретическим называют распределение вероятностей. Теоретические распределения изучает теория вероятностей. В этом параграфе рассматриваются теоретические распределения.

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

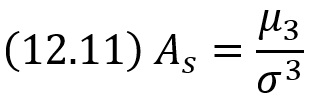
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.

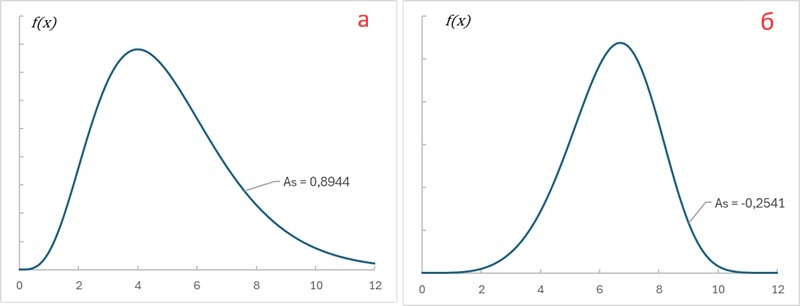
Рис. 4. Распределения а) с правым хвостом на основе гамма распределения, б) с левым хвостом на основе распределения Вейбулла (формулы см. в приложенном Excel-файле)

Для оценки «крутости», т. е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой — эксцессом.

Эксцессом теоретического распределения называют характеристику, которая определяется равенством

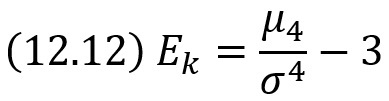
Для нормального распределения эксцесс равен нулю. Если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная (рис. 5а); если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная (рис. 5б).

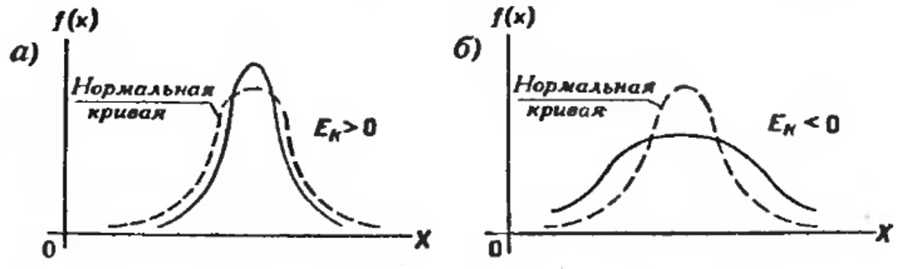
Рис. 5. Эксцесс кривых распределения: а) больше нуля, б) меньше нуля

На самом деле это не так. Например, положительный эксцесс равный трем имеют, как t-распределение Стьюдента с df = 6, так и стандартное распределение Лапласа:

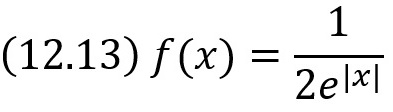
При том, что первое имеет более плоскую вершину, а второе – более острую, в сравнении с нормальным распределением (см. также Эксцесс распределения случайной величины):

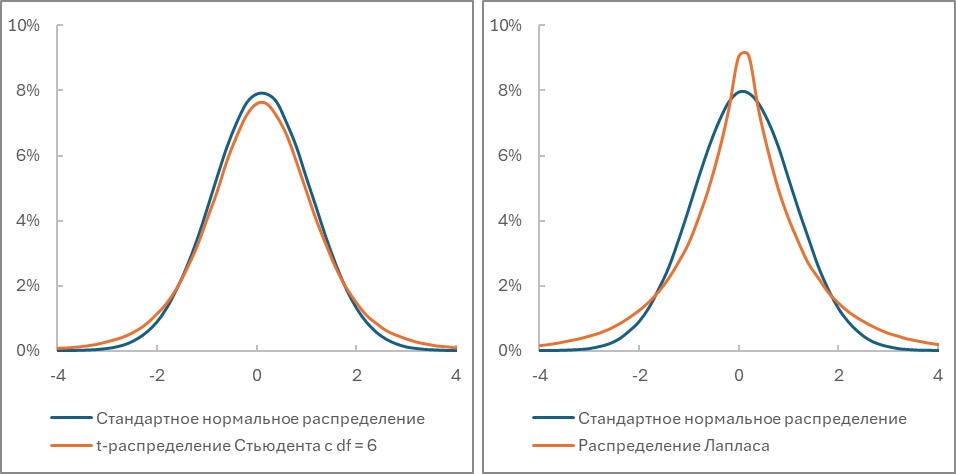
Рис. 6. Влияние толстых хвостов: а) t-распределение Стьюдента с df = 6; б) стандартное распределение Лапласа; в обоих случаях E_k = 3

Поскольку эксцесс пропорционален четвертой степени отклонения случайной величины от среднего, то возрастает роль больших отклонений, т.е. хвоста. Положительный эксцесс обусловлен более тяжелыми хвостами относительно нормального распределения, отрицательный – более легкими.

Функция одного случайного аргумента и ее распределение

Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y = φ(Х). Как найти распределение функции Y = φ(Х), зная плотность распределения случайного аргумента Х? Доказано: если у = φ(х) – дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой х = ψ(у), то плотность распределения g(y) случайной величины Y

Распределение суммы независимых слагаемых. Устойчивость нормального распределения

Плотность распределения суммы независимых случайных величин называют композицией. Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых).

Например, если X и Y — независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными a₁ = 3, а₂ = 4, D₁ = 1, D₂ = 0,5, то композиция этих величин (т. е. плотность вероятности суммы Z = X + Y) также распределена нормально, причем математическое ожидание и дисперсия композиции соответственно равны а = 3 + 4 = 7; D =1 + 0,5 = 1,5.

Распределение «хи квадрат»

Пусть Х_i (i = 1, 2, …, n) – нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице. Тогда сумма квадратов этих величин

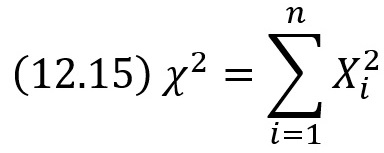
распределена по закону χ² («хи квадрат») с k = n степенями свободы; если же эти величины связаны одним линейным соотношением, например ΣX_i = nХ̅, то число степеней свободы k = n – 1.

Плотность этого распределения

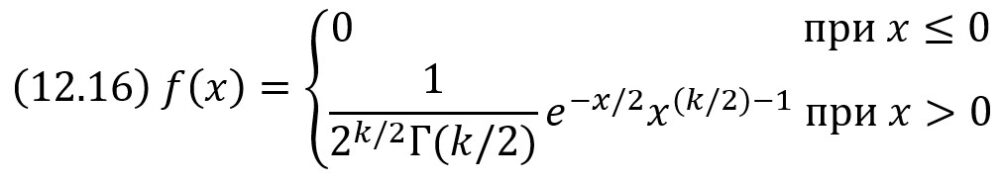
где…

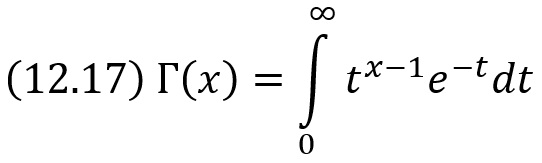
… есть гамма-функция; в частности, Г(n + 1) = n!

Отсюда видно, что распределение «хи квадрат» определяется одним параметром – числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Распределение Стьюдента

Пусть Z – нормальная случайная величина, причем M(Z) = 0, σ(Z) = 1, а V – независимая от Z величина, которая распределена по закону χ² с k степенями свободы. Тогда величина

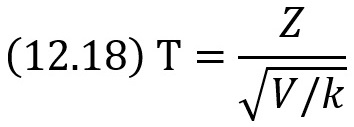
имеет распределение, которое называют t-распределением или распределением Стьюдента (псевдоним английского статистика В. Госсета), с k степенями свободы.

Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Распределение F Фишера — Снедекора

Если U и V – независимые случайные величины, распределенные по закону χ² со степенями свободы k₁ и k₂, то величина

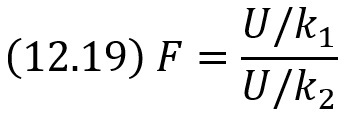
имеет распределение, которое называют распределением F Фишера–Снедекора со степенями свободы k₁ и k₂ (иногда его обозначают через V²).

Плотность этого распределения

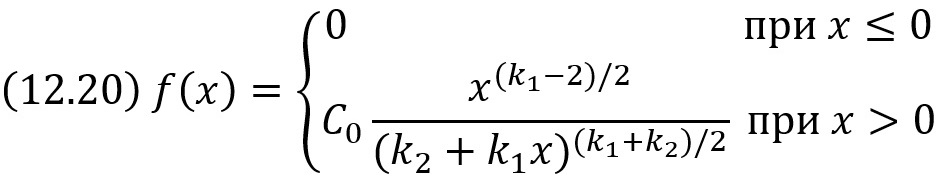
где

Мы видим, что распределение F определяется двумя параметрами – числами степеней свободы.

Глава тринадцатая. ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

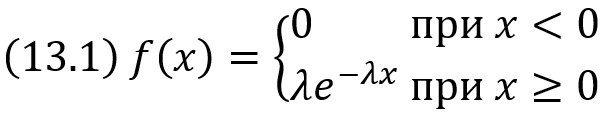
где λ – постоянная положительная величина.

Показательное распределение определяется одним параметром λ. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или более.

Функция распределения показательного закона:

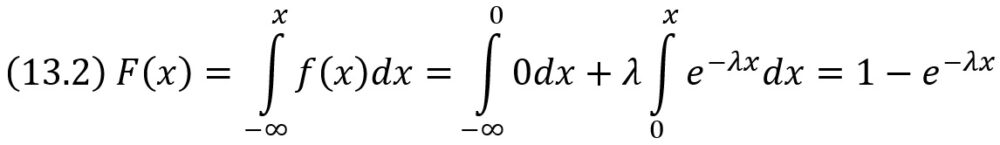
Математическое ожидание показательного распределения M(X) = 1/λ. Среднее квадратическое отклонение σ(X) = 1/λ.

Глава четырнадцатая. СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН

До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, …, n числами.

Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.

Рассмотрим двумерную случайную величину (X, Y). Пусть х, у – пара действительных чисел. Вероятность события, состоящего в том, что X примет значение, меньшее х, и при этом Y примет значение, меньшее у, обозначим через F(х,у). Если х и у будут изменяться, то, вообще говоря, будет изменяться и F(х,у), т. е. F(х,у) есть функция от х и у.

Функцией распределения двумерной случайной величины (X, Y) называют функцию F(х,у), определяющую для каждой пары чисел х, у вероятность того, что X примет значение, меньшее х, и при этом Y примет значение, меньшее у: F(х,у) = P(X<x, Y<y). Геометрически это равенство можно истолковать так: F(х,у) есть вероятность того, что случайная точка (X, Y) попадет в бесконечный квадрант с вершиной (х, у), расположенный левее и ниже этой вершины.

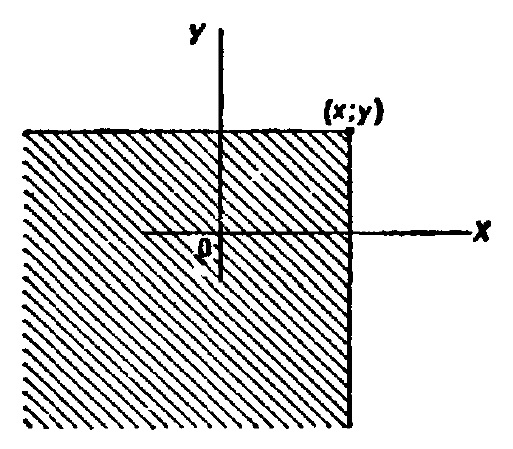
Рис. 7. Геометрическое толкование функции распределения двумерной случайной величины

Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.

Корреляционным моментом случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: μ_xy=М{[Х–М(Х)][Y–М(Y)]}.

Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.

Коэффициентом корреляции r_xy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Так как размерность μ_xy, равна произведению размерностей величин X и Y, σ_х имеет размерность величины X, σ_y имеет размерность величины Y, то r_xy – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.

Линейная регрессия. Прямые линии среднеквадратической регрессии

Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X: Y ≃ g(х) = αХ + β, где α и β – параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них – метод наименьших квадратов.

Функцию g(х) = αХ + β называют «наилучшим приближением» Y в смысле метода наименьших квадратов, если математическое ожидание М[Y – g(X)]² принимает наименьшее возможное значение. Функцию g(x) называют среднеквадратической регрессией Y на X, которая имеет вид

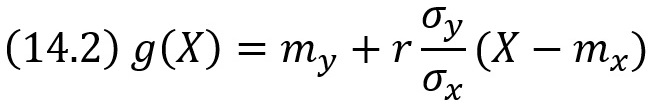
где

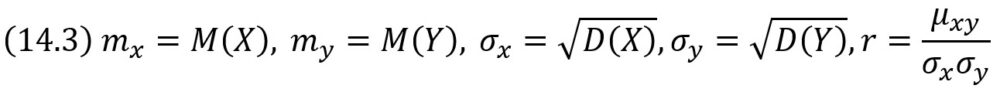
Коэффициент β = rσ_y/σ_x — называют коэффициентом регрессии Y на X, а прямую

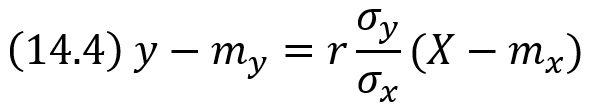
называют прямой среднеквадратической регрессии Y на X.

Величину

называют остаточной дисперсией случайной величины Y относительно случайной величины X; она характеризует величину ошибки, которую допускают при замене Y линейной функцией g(X). При r = ±1 остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от X.

ЧАСТЬ ТРЕТЬЯ. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Глава пятнадцатая. ВЫБОРОЧНЫЙ МЕТОД

Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов. Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:

1. оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
2. проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.

Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раз, x_k – n_k раз и Σn_i = n – объем выборки. Наблюдаемые значения х_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки n_i/n = W_i – относительными частотами.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(х), определяющую для каждого значения х относительную частоту события X < х. F*(х) = n_x/n.

В отличие от эмпирической функции распределения выборки функцию распределения F(х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(х) определяет вероятность события X < х, а эмпирическая функция F*(х) определяет относительную частоту этого же события. При больших n числа F*(х) и F(х) мало отличаются одно от другого. Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Глава шестнадцатая. СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.

Пусть Θ* – статистическая оценка неизвестного параметра Θ теоретического распределения. Допустим, что по выборке объема n найдена оценка Θ₁*. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку Θ₂*. Повторяя опыт многократно, получим числа Θ₁*, Θ₂*, …, Θ_k*, которые, вообще говоря, различны между собой. Таким образом, оценку Θ* можно рассматривать как случайную величину, а числа Θ₁*, Θ₂*, …, Θ_k* – как ее возможные значения.

Представим себе, что оценка Θ* дает приближенное значение Θ. Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. M[Θ*]= Θ.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения Θ* могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия D(Θ*) может быть значительной. В этом случае найденная по данным одной выборки оценка, например Θ₁*, может оказаться весьма удаленной от среднего значения Θ̅₁*, а значит, и от самого оцениваемого параметра Θ; приняв Θ₁* в качестве приближенного значения Θ, мы допустили бы большую ошибку.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n → ∞ стремится к нулю, то такая оценка оказывается и состоятельной.

Если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.

Групповая, внутригрупповая, межгрупповая и общая дисперсии

Допустим, что все значения количественного признака X совокупности, безразлично — генеральной или выборочной, разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю и дисперсию значений признака, принадлежащих группе, относительно групповой средней.

Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней

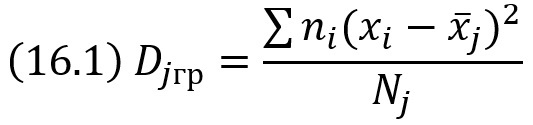
где n_i – частота значения х_i, j – номер группы; x̅_j – групповая средняя группы j; N_j = Σn_i – объем группы j.

Зная дисперсию каждой группы, можно найти их среднюю арифметическую.

Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:

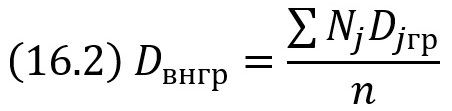
где N_j – объем группы j, n = ΣN_j – объем всей совокупности.

Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.

Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:

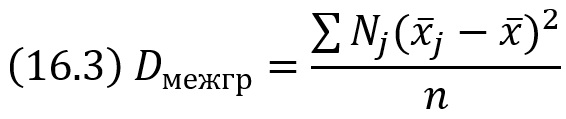
где x̅_j – групповая средняя группы j; N_j – объем группы j; х̅ – общая средняя; n – объем всей совокупности.

Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:

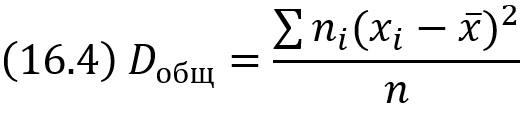
где n_i – частота значения х_i, х̅ – общая средняя; n – объем всей совокупности.

Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий: D_общ = D_внгр + D_межгр.

Оценка генеральной дисперсии по исправленной выборочной

Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Выборочная дисперсия является смещенной оценкой D_г. В качестве оценки генеральной дисперсии принимают исправленную дисперсию

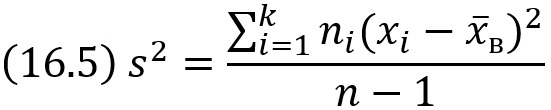
Подчеркнем, что s не является несмещенной оценкой; чтобы отразить этот факт, мы написали «исправленное» среднее квадратическое отклонение.

Точность оценки, доверительная вероятность (надежность). Доверительный интервал

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, – точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ – Θ*|. Другими словами, если δ > 0 и |Θ – Θ*|< δ, то чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Θ* удовлетворяет неравенству |Θ – Θ*|< δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с которой осуществляется неравенство |Θ – Θ*|< δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что |Θ – Θ*|< δ, равна γ

Это соотношение следует понимать так: вероятность того, что интервал (Θ* – δ, Θ* + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.

Доверительным называют интервал (Θ* – δ, Θ* + δ), который покрывает неизвестный параметр с заданной надежностью γ.

Так как случайной величиной является не оцениваемый параметр Θ, а доверительный интервал, то более правильно говорить не о вероятности попадания Θ в доверительный интервал, а о вероятности того, что доверительный интервал покроет Θ.

Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней х̅.

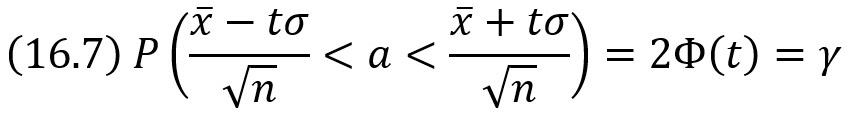
где γ – заданная надежность, t = δ√n/σ.

Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал (х̅ – tσ/√n, х̅ + tσ/√n) покрывает неизвестный параметр а; точность оценки δ = tσ/√n.

При возрастании объема выборки n число δ убывает и, следовательно, точность оценки увеличивается. Увеличение надежности оценки γ = 2Ф(t) приводит к увеличению t (Ф(t) –возрастающая функция), следовательно, и к возрастанию δ; другими словами, увеличение надежности влечет за собой уменьшение ее точности.

Пример. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением σ = 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним х̅, если объем выборки n = 36 и задана надежность оценки γ = 0,95.

Решение. Найдем t. Из соотношения 2Ф(t) = 0,95 получим Ф(t) = 0,475. По таблицам находим t =1,96.

Найдем точность оценки:

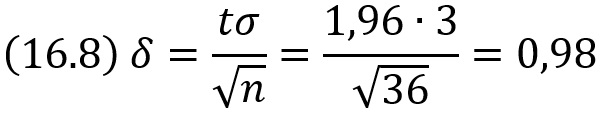
Доверительный интервал таков: (х̅ – 0,98; х̅ + 0,98). Например, если х̅ = 4,1, то доверительный интервал имеет следующие доверительные границы: х̅ – 0,98 = 4,1 – 0,98 = 3,12; х̅ + 0,98 = 4,1 + 0,98 = 5,08.

Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08. Подчеркнем, что было бы ошибочным написать Р(3,12 < а < 5,08) = 0,95. Действительно, так как а – постоянная величина, то либо она заключена в найденном интервале (тогда событие 3,12 < а < 5,08 достоверно и его вероятность равна единице), либо в нем не заключена (в этом случае событие 3,12 < а < 5,08 невозможно и его вероятность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром; она связана лишь с границами доверительного интервала, которые, как уже было указано, изменяются от выборки к выборке.

Поясним смысл, который имеет заданная надежность. Надежность γ = 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.

Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором σ предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t):

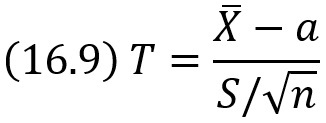
которая имеет распределение Стьюдента с k = n – 1 степенями свободы; здесь X̅ – выборочная средняя, S – «исправленное» среднее квадратическое отклонение, n – объем выборки.

Плотность распределения Стьюдента

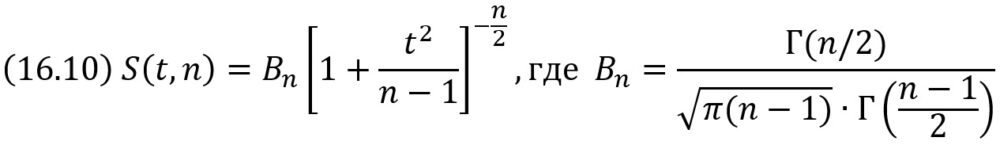
Мы видим, что распределение Стьюдента определяется параметром n – объемом выборки (или числом степеней свободы k = n – 1) и не зависит от неизвестных параметров а и σ; эта особенность является его большим достоинством. Поскольку S(t,n) – четная функция от t, вероятность осуществления неравенства

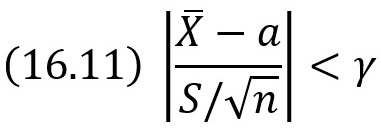
определяется

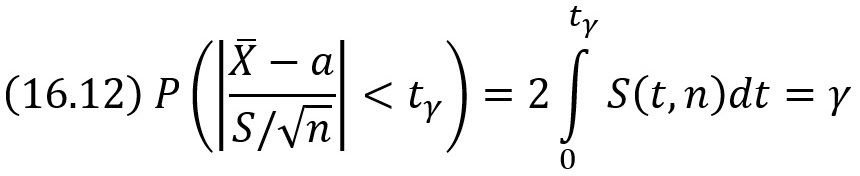
Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим

Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал, покрывающий. неизвестный параметр а с надежностью γ. Здесь случайные величины X̅ и S заменены неслучайными величинами х̅ и s, найденными по выборке. По таблице по заданным n и γ можно найти t_γ.

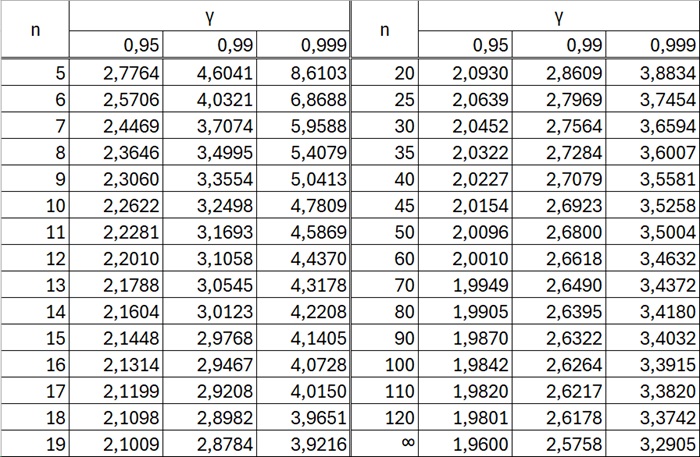
Рис. 8. Таблица значений t_γ = t(γ, n)

В Excel значение можно найти с помощью формулы =СТЬЮДЕНТ.ОБР(1-(1-γ)/2;n-1).

При неограниченном возрастании объема выборки n распределение Стьюдента стремится к нормальному. Значения в таблице для n = ∞ найдены по формуле =НОРМ.СТ.ОБР(1-(1- γ)/2). Поэтому практически при п > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением.

Для малых выборок (n < 30) замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если n = 5 и γ = 0,99, то, пользуясь распределением Стьюдента, найдем t_γ = 4,6, а используя функцию Лапласа, найдем t_γ = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

Метод моментов для точечной оценки параметров распределения

Можно доказать, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. На этом основан метод моментов, предложенный К. Пирсоном. Достоинство метода — сравнительная его простота. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.

А. Оценка одного параметра. Пусть задан вид плотности распределения f (х, Θ), определяемой одним неизвестным параметром Θ. Требуется найти точечную оценку параметра Θ.

Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν₁ = M₁. Учитывая, что ν₁ = М(X), М₁ = х̅_B, получим

Математическое ожидание М(X), как видно из соотношения

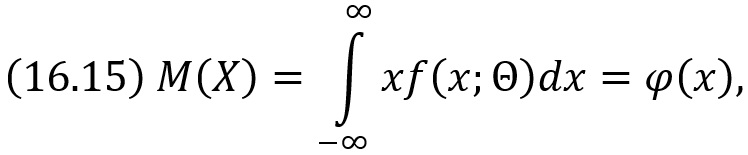
есть функция от Θ, поэтому (16.13) можно рассматривать как уравнение с одним неизвестным Θ. Решив это уравнение относительно параметра Θ, тем самым найдем его точечную оценку Θ*, которая является функцией от выборочной средней, следовательно, и от вариант выборки:

Пример. Найти методом моментов по выборке х₁, х₂, …, x_n точечную оценку неизвестного параметра λ показательного распределения, плотность распределения которого f(x) = λe^–λx (x≥0).

Решение. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν₁ = M₁. Учитывая, что ν₁ = М(X), М₁ = х̅_B, получим М(X)= х̅_B. Приняв во внимание, что математическое ожидание показательного распределения равно 1/λ, имеем 1/λ = х̅_B. Отсюда λ = 1/х̅_B. Итак, искомая точечная оценка параметра λ, показательного распределения равна величине, обратной выборочной средней: λ* = 1/х̅_B.

Б. Оценка двух параметров. Пусть задан вид плотности распределения f (х, Θ₁, Θ₂), определяемой неизвестными параметрами Θ₁ и Θ₂. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: ν₁ = M₁, μ₂ = M₂.

Учитывая, что ν₁ = М(X), μ₂ = D(X), M₁ = х̅_B, m₂ = D_B, получим М(X) = х̅_B, D(X) = D_B. Математическое ожидание и дисперсия есть функции от Θ₁ и Θ₂, поэтому два последних равенства можно рассматривать как систему двух уравнений с двумя неизвестными Θ₁ и Θ₂. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки Θ*₁ и Θ*₂. Эти оценки являются функциями от вариант выборки:

Пример. Найти методом моментов по выборке х₁, х₂, …, x_n точечные оценки неизвестных параметров а и σ нормального распределения

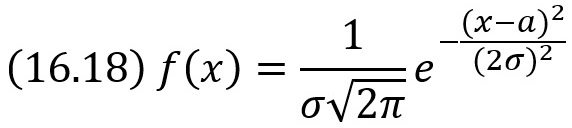
Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка: ν₁ = M₁, μ₂ = M₂. Учитывая, что ν₁ = М(X), μ₂ = D(X), M₁ = х̅_B, m₂ = D_B, получим М(X) = х̅_B, D(X) = D_B. Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна σ², имеем: а = х̅_B, σ² = D_B. Итак, искомые точечные оценки параметров нормального распределения: а* = х̅_B, σ* = √D_B.

Метод наибольшего правдоподобия

Кроме метода моментов существуют и другие методы точечной оценки неизвестных параметров распределения. К ним относится метод наибольшего правдоподобия, предложенный Р. Фишером.

А. Дискретные случайные величины. Пусть X – дискретная случайная величина, которая в результате n испытаний приняла значения х₁, х₂, …, x_n. Допустим, что вид закона распределения величины X задан, но неизвестен параметр Θ, которым определяется этот закон. Требуется найти его точечную оценку.

Обозначим вероятность того, что в результате испытания величина X примет значение x_i (i = 1, 2, …, n), через p(x_i; Θ). Функцией правдоподобия дискретной случайной величины X называют функцию аргумента Θ: L(x₁, х₂, …, х_n; Θ) = р(х₁; Θ)р(х₂; Θ) … р (х_n; Θ), где х₁, х₂, …, x_n – фиксированные числа.

В качестве точечной оценки параметра Θ принимают такое его значение Θ* = Θ*(х₁, х₂, …, x_n), при котором функция правдоподобия достигает максимума. Оценку Θ* называют оценкой наибольшего правдоподобия.

Функции L и lnL достигают максимума при одном и том же значении Θ, поэтому вместо отыскания максимума функции L ищут (что удобнее) максимум функции lnL.

Логарифмической функцией правдоподобия называют функцию lnL. Как известно, точку максимума функции lnL аргумента Θ можно искать, например, так:

найти производную

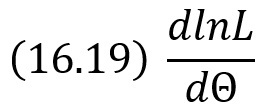
приравнять производную нулю и найти критическую точку – корень полученного уравнения (его называют уравнением правдоподобия);

найти вторую производную

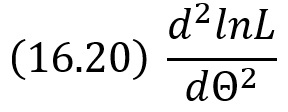
если вторая производная при Θ = Θ* отрицательна, то Θ* – точка максимума.

Найденную точку максимума Θ* принимают в качестве оценки наибольшего правдоподобия параметра Θ.

Функция правдоподобия – функция от аргумента Θ; оценка наибольшего правдоподобия – функция от независимых аргументов х₁, х₂, …, x_n. Оценка наибольшего правдоподобия не всегда совпадает с оценкой, найденной методом моментов.

Пример. Найти методом наибольшего правдоподобия оценку параметра X распределения Пуассона

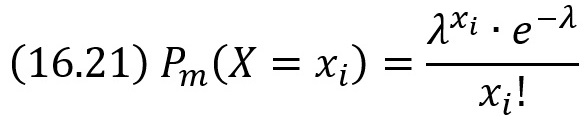
где m – число произведенных испытаний; х_i – число появлений события в i-м (i = 1, 2, …, n) опыте (опыт состоит из m испытаний).

Решение. Составим функцию правдоподобия, учитывая, что Θ = λ:

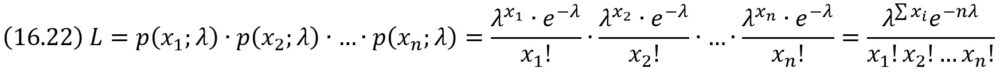
Найдем логарифмическую функцию правдоподобия:

Найдем первую производную по λ:

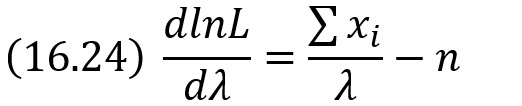
Напишем уравнение правдоподобия, для чего приравняем первую производную нулю:

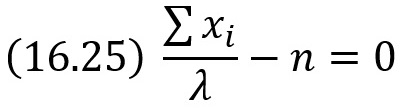
Найдем критическую точку, для чего решим полученное уравнение относительно λ:

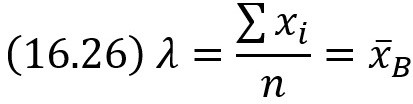
Найдем вторую производную по λ:

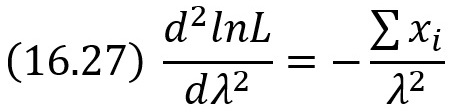
При λ = х̅_B вторая производная отрицательна; следовательно, λ = х̅_B – точка максимума и, значит, в качестве оценки наибольшего правдоподобия параметра λ распределения Пуассона надо принять выборочную среднюю λ* = х̅_B.

Глава семнадцатая. МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ

Условные варианты

Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда. Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Условными называют варианты, определяемые равенством u_i = (x_i – C)/h, где С – ложный нуль (новое начало отсчета); h – шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба). Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.

Если вариационный ряд состоит из равноотстоящих вариант с шагом h, то условные варианты есть целые числа.

Обычные, начальные и центральные эмпирические моменты

Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов. В отличие от теоретических эмпирические моменты вычисляют по данным наблюдений. Обычным эмпирическим моментом порядка k называют среднее значение k-х степеней разностей x_i – C:

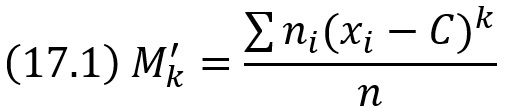
где x_i – наблюдаемая варианта, n_i – частота варианты, n = Σn_i – объем выборки, C – произвольное постоянное число (ложный нуль).

Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С = 0

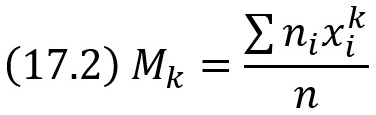
В частности,

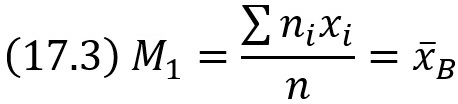
т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка k называют обычный момент порядка k при С = х̅_B

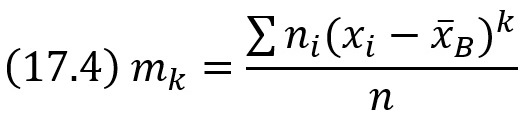
В частности,

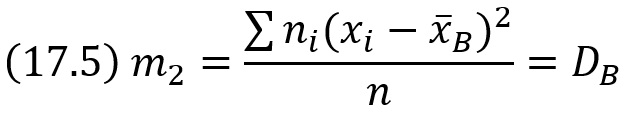
Условные эмпирические моменты

Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными. Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант:

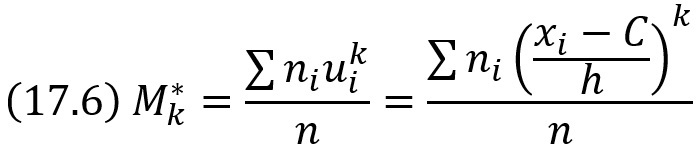
В частности,

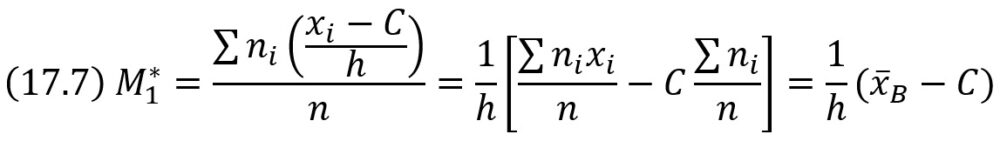
Отсюда х̅_B = M*₁h + C. Таким образом, для того чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль C.

Глава восемнадцатая. ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ

Функциональная, статистическая и корреляционная зависимости

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.

Пусть Y – урожай зерна, X – количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, т. е. Y связан с X корреляционной зависимостью.

Выборочный коэффициент корреляции

Выборочный коэффициент корреляции определяется равенством

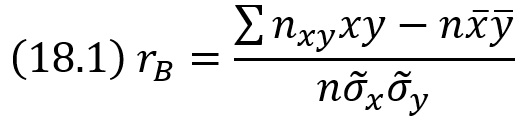
где х, у – варианты (наблюдавшиеся значения) признаков X и Y; n_ху – частота пары вариант (х, у); n –объем выборки (сумма всех частот); σ̃_х, σ̃_y – выборочные средние квадратические отклонения; х̅, у̅ –выборочные средние.

Предварительные соображения к введению меры любой корреляционной связи

Пусть данные наблюдений над количественными признаками X и Y сведены в корреляционную таблицу. Можно считать, что тем самым наблюдаемые значения Y разбиты на группы; каждая группа содержит те значения Y, которые соответствуют определенному значению X. Например, дана корреляционная таблица:

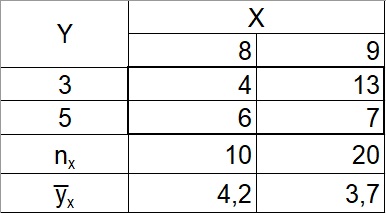
Рис. 9. Корреляционная таблица

К первой группе относятся те 10 значений Y (4 раза наблюдалось y₁ = З и 6 раз y₂ = 5), которые соответствуют х₁ = 8. Ко второй группе относятся те 20 значений Y (13 раз наблюдалось y₁ = З и 7 раз y₂ = 5), которые соответствуют х₁ = 9.

Условные средние теперь можно назвать групповыми средними: групповая средняя первой группы у̅₈ = (4*3 + 6*5)/10 = 4,2; групповая средняя второй группы у̅₉ = (13*3 + 7*5)/20 = 3,7. Поскольку все значения признака Y разбиты на группы, можно представить общую дисперсию признака в виде суммы внутригрупповой и межгрупповой дисперсий: D_общ = D_внгр + D_межгр. Если Y связан с X функциональной зависимостью, то D_межгр / D_общ = 1. Если Y связан с X корреляционной зависимостью, то D_межгр / D_общ < 1.

Чем связь между признаками ближе к функциональной, тем меньше D_внгр следовательно, тем больше приближается D_межгр к D_общ, а значит, отношение D_межгр / D_общ – к единице. Отсюда ясно, что целесообразно рассматривать в качестве меры тесноты корреляционной зависимости отношение межгрупповой дисперсии к общей, или, что то же, отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению.

Корреляционным отношением η называют отношение σ_межгр к σ_общ

Корреляционное отношение как мера корреляционной связи

Поскольку в рассуждениях не делалось никаких допущений о форме корреляционной связи, η служит мерой тесноты связи любой, в том числе и линейной, формы. В этом состоит преимущество корреляционного отношения перед коэффициентом корреляции, который оценивает тесноту лишь линейной зависимости. Вместе с тем корреляционное отношение обладает недостатком: оно не позволяет судить, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т. д. Эго объясняется тем, что при определении корреляционного отношения форма связи во внимание не принималась.

Глава девятнадцатая. СТАТИСТИЧЕСКАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр Θ равен определенному значению Θ₀, выдвигают гипотезу: Θ = Θ₀. Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и многие другие.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Например, статистическими являются гипотезы: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений. Гипотеза «на Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Нулевой (основной) называют выдвинутую гипотезу Н₀. Конкурирующей (альтернативной) называют гипотезу Н₁ которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а ≠ 10. Коротко это записывают так: Н₀: а=10; Н₁: а ≠ 10.

Различают гипотезы, которые содержат только одно и более одного предположений. Простой называют гипотезу, содержащую только одно предположение. Например, если λ – параметр показательного распределения, то гипотеза Н₀: λ = 5 – простая. Гипотеза Н₀: математическое ожидание нормального распределения равно 3 (σ известно) – простая.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза Н₀: λ > 5 состоит из бесчисленного множества простых вида Н_i: λ = b_i, где b_i – любое число, большее 5. Гипотеза Н₀: математическое ожидание нормального распределения равно 3 (σ неизвестно) – сложная.

Ошибки первого и второго рода

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через α; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).

Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают через U или Z, если она распределена нормально, F или υ² – по закону Фишера–Снедекора, Т – по закону Стьюдента, χ² – по закону «хи квадрат» и т. д. Поскольку в этом параграфе вид распределения во внимание приниматься не будет, обозначим эту величину в целях общности через K.

Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий:

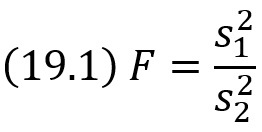
Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперед неизвестные значения, и распределена по закону Фишера–Снедекора. Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением K_набл называют значение критерия, вычисленное по выборкам. Например, если по двум выборкам найдены исправленные выборочные дисперсии s₁ = 20 и s₂ = 5, то наблюдаемое значение критерия F

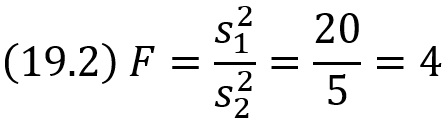
Критическая область. Область принятия гипотезы. Критические точки

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.

Поскольку критерий K – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют. Критическими точками (границами) k_кр называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством K > k_кр, где k_кр – положительное число (рис. 10а). Левосторонней называют критическую область, определяемую неравенством K < k_кр, где k_кр – отрицательное число (рис. 10б). Односторонней называют правостороннюю или левостороннюю критическую область. Двусторонней называют критическую область, определяемую неравенствами K < k₁, K > k₂, где k₂ > k₁. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что k_кр > 0): K < –k_кр, K > k_кр или равносильным неравенством |K| > k_кр (рис. 10в).

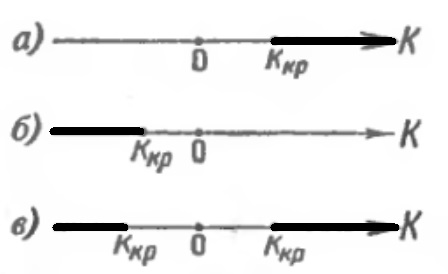
Рис. 10. Односторонние и двусторонняя критические области

Отыскание правосторонней критической области

Как найти критическую область? Для определенности начнем с нахождения правосторонней критической области, которая определяется неравенством K > k_кр, где k_кр > 0. Для отыскания правосторонней критической области достаточно найти критическую точку. Для ее нахождения задаются достаточной малой вероятностью – уровнем значимости α. Затем ищут критическую точку k_кр, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий K примет значение, большее k_кр, была равна принятому уровню значимости: P(K > k_кр) = α.

Для каждого критерия имеются таблицы[1], по которым и находят критическую точку, удовлетворяющую этому требованию.

Когда критическая точка найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что K_набл > k_кр, то нулевую гипотезу отвергают; если же K_набл < k_кр, то нет оснований отвергнуть нулевую гипотезу.

Наблюдаемое значение критерия может оказаться большим k_кр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости α.

Пусть нулевая гипотеза принята; ошибочно думать, что тем самым она доказана. Действительно, известно, что один пример, подтверждающий справедливость некоторого общего утверждения, еще не доказывает его. Поэтому, более правильно говорить данные наблюдений согласуются с нулевой гипотезой и, следовательно, не дают оснований ее отвергнуть.

На практике для большей уверенности принятия гипотезы ее проверяют другими способами или повторяют эксперимент, увеличив объем выборки.

Отвергают гипотезу более категорично, чем принимают. Действительно, известно, что достаточно привести один пример, противоречащий некоторому общему утверждению, чтобы это утверждение отвергнуть. Если оказалось, что наблюдаемое значение критерия принадлежит критической области, то этот факт и служит примером, противоречащим нулевой гипотезе, что позволяет ее отклонить.

Мощность критерия

Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.

Если вероятность ошибки второго рода (принять неправильную гипотезу) равна β, то мощность равна 1 – β.

Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода.

Чем меньше вероятности ошибок первого и второго рода, тем критическая область «лучше». Однако при заданном объеме выборки уменьшить одновременно α и β невозможно; если уменьшить α, то β будет возрастать.

Если α уже выбрано, то, пользуясь теоремой Ю. Неймана и Э. Пирсона, изложенной в более полных курсах, можно построить критическую область, для которой β будет минимальным и, следовательно, мощность критерия максимальной.

Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок.

Сравнение двух дисперсий нормальных генеральных совокупностей

Задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, самих методов измерений и т. д. Очевидно, предпочтительнее тот прибор, инструмент и метод, который обеспечивает наименьшее рассеяние результатов измерений, т. е. наименьшую дисперсию.

Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам с объемами, соответственно равными n₁ и n₂, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии s²_x и s²_y. Требуется по исправленным дисперсиям при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H₀: D(X) = D(Y).

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий примем отношение большей исправленной дисперсии к меньшей, т. е. случайную величину

Величина F при справедливости нулевой гипотезы имеет распределение Фишера–Снедекора со степенями свободы k₁ = n₁ – 1 и k₂ = n₂ – 1, где n₁ – объем выборки, по которой вычислена большая исправленная дисперсия, n₂ – объем выборки, по которой найдена меньшая дисперсия. Напомним, что распределение Фишера–Снедекора зависит только от чисел степеней свободы и не зависит от других параметров.

Критическая область строится в зависимости от вида конкурирующей гипотезы. Если конкурирующая гипотеза H₁: D(X) ≠ D(Y), то строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α.

Наибольшая мощность (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы} достигается тогда, когда вероятность попадания критерия в каждый из двух интервалов критической области равна α/2. Если обозначить через F₁ левую границу критической области и через F₂ – правую, то Р(F < F₁ ) = α/2, Р(F > F₂) = α/2.

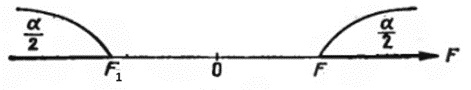
Рис. 11. Критические области при двусторонней конкурирующей гипотезе

Чтобы найти правую критическую точку надо вычислить отношение большей исправленной дисперсии к меньшей (19.3) и по таблице критических точек распределения Фишера–Снедекора по уровню значимости α/2 (вдвое меньшем заданного) и числам степеней свободы k₁ и k₂ (k₁ – число степеней свободы большей дисперсии) найти критическую точку F_кр(α /2; k₁, k₂).

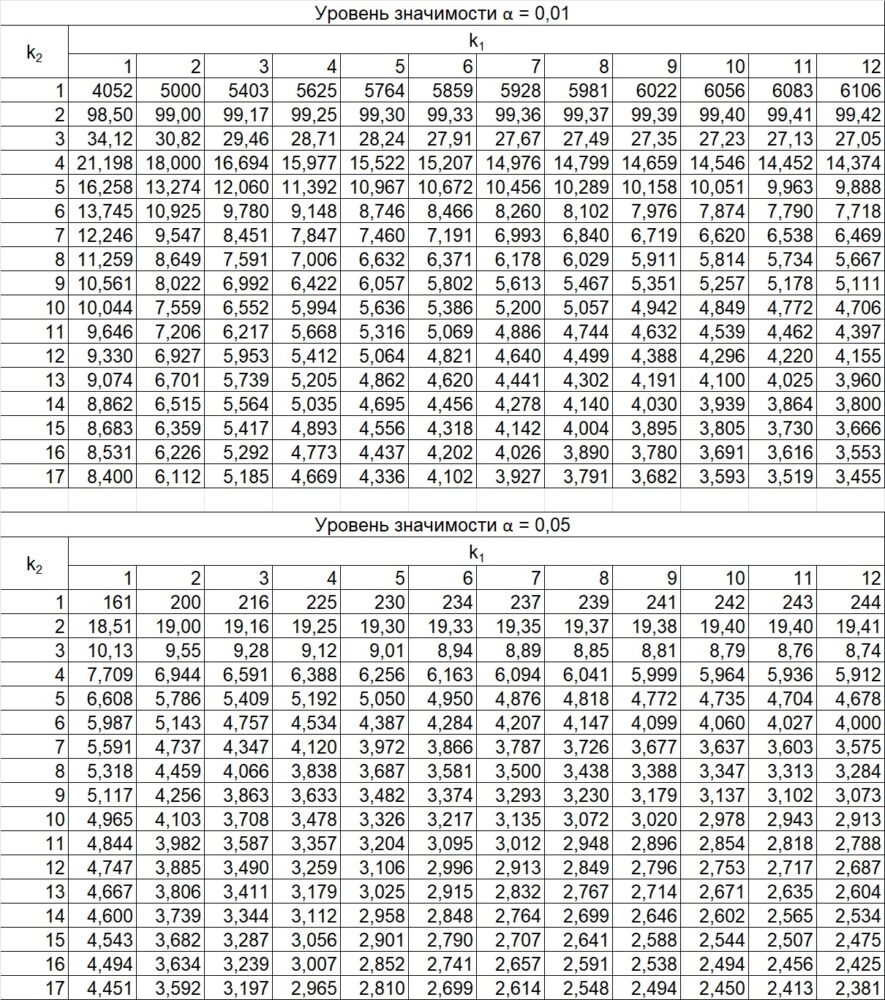
Рис. 12. Критические точки распределения F Фишера–Снедекора (k₁ – число степеней свободы большей дисперсии, k₂ – число степеней свободы меньшей дисперсии). Для отыскания критической точки в Excel воспользуйтесь формулой =F.ОБР(1-α; k₁; k₂).

Если F_набл < F_кр – нет оснований отвергнуть нулевую гипотезу. Если F_набл > F_кр – нулевую гипотезу отвергают.

Далее рассматриваются различные ситуации статистического вывода и различные критерии, в том числе:

• Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
• Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки)
• Сравнение двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки)
• …

ЧАСТЬ ЧЕТВЕРТАЯ. МЕТОД МОНТЕ–КАРЛО. ЦЕПИ МАРКОВА

Глава двадцать первая. МОДЕЛИРОВАНИЕ (РАЗЫГРЫВАНИЕ) СЛУЧАЙНЫX ВЕЛИЧИН МЕТОДОМ МОНТЕ-КАРЛО

Сущность метода Монте–Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно а: М(Х) = а.

Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений X; вычисляют их среднее арифметическое x̅ и принимают х в качестве оценки (приближенного значения) а* искомого числа а: а ≈ а* = х̅

Разыгрывание дискретной случайной величины

Пусть требуется разыграть дискретную случайную величину X, т. е. получить последовательность ее возможных значений x_i (i = 1, 2, …, п), зная закон распределения X:

X            х₁          х₂           …           х_n

P            p₁          p₂          …           p_n

Надо: 1) разбить интервал (0, 1) оси Or на n частичных интервалов: Δ₁ – (0; p₁), Δ₂ – (p₁; p₁ + p₂), …, Δ_n – (p₁ + p₂ +…+ p_n;1); 2) выбрать (например, из таблицы случайных чисел) случайное число r_j. Если r_j попало в частичный интервал Δ_i, то разыгрываемая дискретная случайная величина приняла возможное значение х₁.

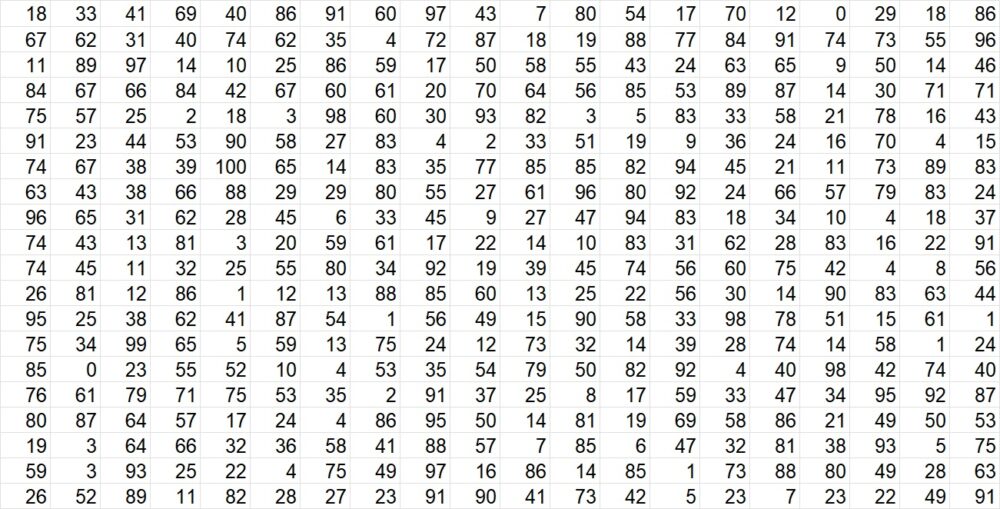
Рис. 13. Равномерно распределенные случайные числа; число – два первых десятичных знака, например, 18 –> 0,18. В Excel случайное число в диапазоне (0, 1) можно получить формулой =СЛЧИС()

Пример. Разыграть 8 значений дискретной случайной величины X, закон распределения которой задан в виде таблицы

X            3           11         24

p            0,25      0,16      0,59

Разобьем интервал  (0, 1) оси Or точками с координатами 0,25; 0,25 + 0,16 = 0,41 на 3 интервала: Δ₁ – (0; 0,25), Δ₂ – (0,24; 0,41), Δ₃ – (0,41; 1). Выпишем из таблицы восемь случайных чисел, например: 0,18; 0,67; 0,11; 0,84; 0,75; 0,91; 0,74; 0,63.

Случайное число r₁ = 0,18 принадлежит частичному интервалу Δ₁, поэтому разыгрываемая дискретная случайная величина приняла возможное значение х₁ = 3. Случайное число r₂ = 0,67 принадлежит частичному интервалу Δ₃, поэтому разыгрываемая величина приняла возможное значение х₃ = 24. Аналогично получим остальные возможные значения.

Итак, разыгранные возможные значения X таковы: 3; 24; 3; 24; 24; 24; 24; 24.

Разыгрывание непрерывной случайной величины. Метод обратных функций

Пусть требуется разыграть непрерывную случайную величину X, т. е. получить последовательность ее возможных значений x_i (i = 1, 2, …, п), зная функцию распределения F(х).

Теорема. Если r_i – случайное число, то возможное значение x_i разыгрываемой непрерывной случайной величины X с заданной функцией распределения F(х), соответствующее r_i, является корнем уравнения F(х_i) = r_i.

Доказательство. Пусть выбрано случайное число r_i (0 < r_i < 1). Так как в интервале всех возможных значений X функция распределения F(х) монотонно возрастает от 0 до 1, то в этом интервале существует, причем только одно, такое значение аргумента х_i при котором функция распределения примет значение r_i. Другими словами, уравнение F(х_i) = r_i имеет единственное решение

где F^-1 – функция, обратная функции y = F(x).

Если решить это уравнение в явном виде не удается, то прибегают к графическим или численным методам.

Пример. Непрерывная случайная величина X распределена по показательному закону, заданному функцией распределения (параметр λ > 0 известен)

Требуется найти явную формулу для разыгрывания возможных значений X.

Решение. Используя правило (21.1) напишем уравнение

Решим это уравнение относительно х_i:

Отсюда

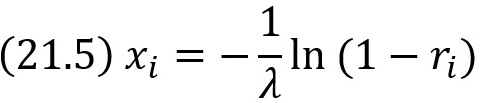
Случайное число r_i заключено в интервале (0, 1); следовательно, число 1 – r_i также случайное и принадлежит интервалу (0,1). Другими словами, величины R и 1 – R распределены одинаково. Поэтому для отыскания х_i можно воспользоваться более простой формулой

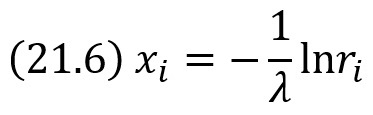
Известно, что

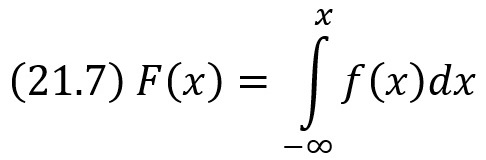
В частности,

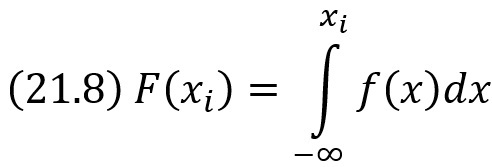
Отсюда следует, что если известна плотность вероятности f(х), то для разыгрывания X можно вместо уравнений F(х_i) = r_i решить относительно х_i уравнение

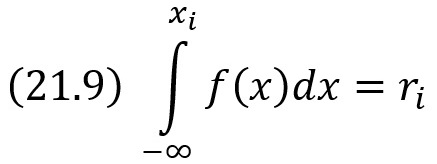
Для того чтобы найти возможное значение х_i непрерывной случайной величины X, зная ее плотность вероятности f(х), надо выбрать случайное число r_i и решить относительно х_i уравнение (21.8) или уравнение

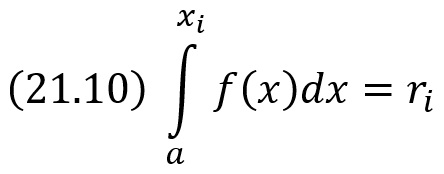
где а – наименьшее конечное возможное значение X.

Пример. Задана плотность вероятности непрерывной случайной величины X f(х) = λ(1–λx/2) в интервале (0; 2/λ); вне этого интервала f(х) = 0. Требуется найти явную формулу для разыгрывания возможных значений X.

Решение. Напишем в соответствии с правилом (21.9) уравнение

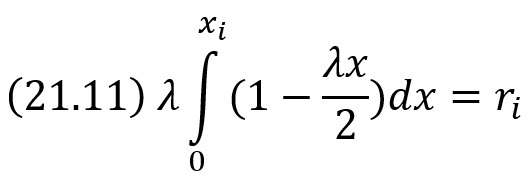
Выполнив интегрирование и решив полученное квадратное уравнение относительно х_i, получим

Глава двадцать вторая. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ЦЕПЯХ МАРКОВА

Цепью Маркова называют последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A₁, А₂, …, A_k полной группы, причем условная вероятность p_ij(s) того, что в s-м испытании наступит событие A_j(j = 1, 2, …,k), при условии, что в (s – 1)-м испытании наступило событие A_i(i = 1, 2, …. k), не зависит от результатов предшествующих испытаний.

Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий A₁, А₂, А₃, A₄, причем известно, что в шестом испытании появилось событие А₂, то условная вероятность того, что в седьмом испытании наступит событие А₄, не зависит от того, какие события появились в первом, втором, …. пятом испытаниях.

Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, от появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний.

Далее используется терминология, которая принята при изложении цепей Маркова. Пусть некоторая система в каждый момент времени находится в одном из k состояний: первом, втором, …. k-м. В отдельные моменты времени в результате испытания состояние системы изменяется, т. е. система переходит из одного состояния, например i, в другое, например j. В частности, после испытания система может остаться в том же состоянии («перейти» из состояния i в состояние j = i).

Таким образом, события называют состояниями системы, а испытания – изменениями ее состояний. Дадим теперь определение цепи Маркова, используя новую терминологию.

Цепью Маркова называют последовательность испытаний, в каждом из которых система принимает только одно из k состояний полной группы, причем условная вероятность p_ij(s) того, что в s-м испытании система будет находиться в состоянии j, при условии, что после (s – 1)-го испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

Однородная цепь Маркова. Переходные вероятности. Матрица перехода

Однородной называют цепь Маркова, если условная вероятность p_ij(s) (перехода из состояния i в состояние j) не зависит от номера испытания. Поэтому вместо p_ij(s) пишут просто p_ij.

Пример. Случайное блуждание. Пусть на прямой Ох в точке с целочисленной координатой х = п находится материальная частица. В определенные моменты времени t₁, t₂, t₃, … частица испытывает толчки. Под действием толчка частица с вероятностью р смещается на единицу вправо и с вероятностью 1 – р – на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков.

Таким образом, случайное блуждание – пример однородной цепи Маркова с дискретным временем.

Переходной вероятностью p_ij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние j.

Таким образом, в обозначении p_ij первый индекс указывает номер предшествующего, а второй – номер последующего состояния. Например, p₁₁ — вероятность «перехода» из первого состояния в первое; p₂₃ — вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

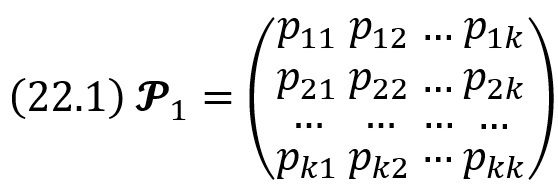
Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния i в любое возможное состояние j), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

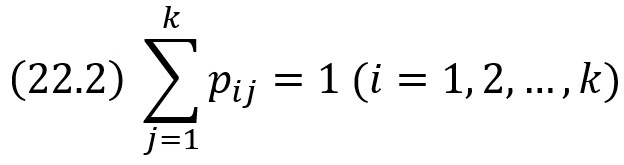
Приведем пример матрицы перехода системы, которая может находиться в трех состояниях:

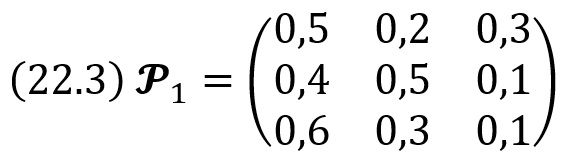
Здесь p₁₁ = 0,5 – вероятность перехода из состояния i = 1 в это же состояние j = 1; p₂₁ = 0,4 – вероятность перехода из состояния i = 2 в состояние j = 1.

Равенство Маркова

Обозначим через P_ij(n) вероятность того, что в результате n шагов (испытаний) система перейдет из состояния i в состояние j. Например, P₂₅(10) – вероятность перехода за 10 шагов из второго состояния в пятое.

Подчеркнем, что при n = 1 получим переходные вероятности P_ij(1) = p_ij.

Поставим перед собой задачу: зная переходные вероятности p_ij, найти вероятности P_ij(n) перехода системы из состояния i в состояние j за п шагов. С этой целью введем в рассмотрение промежуточное (между i и j) состояние r. Другими словами, будем считать, что из первоначального состояния i за m шагов система перейдет в промежуточное состояние r с вероятностью P_ir(m), после чего за оставшиеся n – m шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью P_rj(n–m).

По формуле полной вероятности

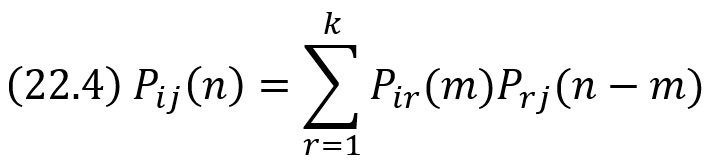
Эту формулу называют равенством Маркова.

 

[1] А для многих критериев есть формулы в Excel.