Книга известного советского популяризатора науки представляет из себя набор эссе о различных аспектах теории вероятностей, статистическом выводе и планировании эксперимента. Будет интересна тем, кто любит математику и статистику. Некоторые разделы вовсе не содержат формул. В некоторых – формулы присутствуют, но для их понимания школьной программы будет достаточно. Я приведу отдельные высказывания, которые мне показались наиболее интересными.
Яков Хургин. Да, нет или может быть… Рассказы о статистической теории управления и эксперимента. – М.: ЛЕНАНД, 2021. – 208 с. Это репринтное издание 1977 г.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 7% от объема книги)
Купить книгу в Ozon
Неопределенность и случайность
Пусть число наблюдений велико, и вы выбираете заранее какое-либо подмножество наблюдений, например каждое третье или первые сто пятнадцать в каждой тысяче. Тогда нужно, чтобы частоты наступлений изучаемого события, вычисленные по всем наблюдениям и по отобранному подмножеству, были близки. Если изучаемое событие обладает такими свойствами, то оно называется случайным. Именно в этих условиях вводится понятие вероятности наступления события, как обобщение частоты его наступления, причем вводится аксиоматически.
С другой стороны, исход олимпийских игр, скажем, по спортивной гимнастике, завоевавшей интерес широкого зрителя, заранее предсказать нельзя. С позиций теории вероятностей исход олимпийских игр не есть случайное событие: нельзя повторять олимпийские игры многократно в одних и тех же условиях. На следующих играх будут другие участники, другое место проведения игр и т.д. Такие события, в отличие от случайных, называют неопределенными. С математических позиций они изучаются в теории игр. В этой книжке будет рассказано главным образом о случайных событиях, и поэтому основным аппаратом служит теория вероятностей и математическая статистика.
Управление
Говоря об управлении, мы будем подразумевать наличие неопределенности, в условиях которой происходит последовательный процесс выдвижения и проверки гипотез, принятия решений и проверки их правильности.
Остап Бендер принимает решение
Гипотезы обычно обозначают буквой Н (от греческого Нypotesis). Исходную гипотезу или нуль-гипотезу будем обозначать Н0, а конкурирующую или альтернативную, то есть противоположную исходной, будем обозначать Н1. Однако, принимая решение на основании гипотезы можно ошибиться. Ошибка, при которой нуль-гипотеза на самом деле верна (Корейко — миллионер), а принимается альтернативная гипотеза (Корейко — простой счетовод), называют ошибкой первого рода или пропуском (здесь Остап «пропускает» миллионера, за которым охотится). Эту ошибку Остап совершит, если он откажется от «охоты» на Корейко, не поверив Балаганову, в ситуации, когда Корейко на самом деле подпольный миллионер.
Но, возможно, Шура Балаганов ошибся, и на самом деле Корейко — счетовод. Если при этом Остап принимает гипотезу о наличии у Корейко миллионов, то он потратит время и весьма скудные наличные средства на поиски несуществующего миллионера и в результате лишь познакомится со счетоводом, с которого не получишь даже «возмещения расходов». Это есть ошибка второго рода, или ложная тревога. Здесь нулевая гипотеза принимается, хотя она и не верна.
Немного о критериях
В одной и той же задаче при выборе лучшего объекта или лучшего решения всегда можно предложить множество самых различных критериев. При этом весьма эфемерны рассуждения о справедливых и несправедливых решениях, когда оценка ситуации и выбор критерия достаточно произвольны.
Не пропустить бы радиозайчик
Допустим, вы занимаетесь радиолокацией. Гипотеза Н0 – есть только шум и H1 – есть и сигнал, и шум. Ошибка первого рода — это ситуация, когда никакого объекта нет, иначе говоря, есть только шум, а принимается гипотеза Н1 о наличии сигнала и шума, то есть ложная тревога. В математической статистике вероятность ошибки первого рода или вероятность ложной тревоги носит название уровня значимости α. Ситуацию можно представить в виде таблицы:

Рис. 1. Сигнал и шум
Отношение правдоподобия
Попробуем выяснить, меняется ли от поколения к поколению величина среднего роста, считая распределение роста нормальным. Обширные статистические данные говорят, что средний рост взрослых мужчин родившихся в 1908–1913 годах = 162 см. А для небольшой группы мужчин, родившихся между 1943 и 1948 годами, вы подсчитали, что средний рост равен 170 см. Гипотеза, подлежащая проверке, состоит в том, что средний рост от поколения к поколению не меняется, а имеющиеся колебания (162 см и 170 см) – это просто результат естественного разброса, поскольку средний рост – случайная величина. Примем в качестве нулевой гипотезы, что средний рост в поколении родившихся в 1943–1948 годах тот же, что и в поколении родившихся в 1908–1913 годах. Альтернативная гипотеза – средний рост за эти тридцать пять лет увеличился.
Представим плотности вероятностей роста при каждой из гипотез, причем «левая» кривая соответствует H0. Обратимся к группе наблюдаемых мужчин более позднего поколения и проверим рост первого из них (скажем, первого по алфавиту). Пусть он оказался 164 см. Если он из «левой» группы, то он обладает ростом 164 см с плотностью вероятности, равной высоте отрезка, параллельного вертикальной оси, над числом 164 до левой кривой, то есть более высокого отрезка. Если же наблюдаемый мужчина принадлежит к группе с предполагаемым новым распределением вероятностей, график плотности которого — «правая» кривая, то он будет обладать ростом 164 см с плотностью вероятности, равной высоте аналогичного отрезка над числом 164, но уже до правой кривой. Нам надо принять решение — отнести наблюдаемое значение к одному из этих двух распределений. Предлагаемый принцип принятия решения заключается в выборе того из распределений, к которому наблюдение относится с большей вероятностью. В данном случае больше вероятность для нулевой гипотезы.
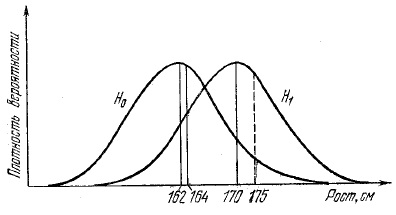
Рис. 2. Плотность вероятности Н0 и Н1
Отношение плотностей вероятности носит название отношения правдоподобия. Отношение правдоподобия сравнивается с единицей, и в зависимости от того, оказывается ли оно больше или меньше единицы, выбирается «левая» или «правая» гипотеза, то есть выбирается более правдоподобное решение.
Если рост второго мужчины 175 см, то с помощью тех же рассуждений следует принять гипотезу о его принадлежности к «правому» распределению. Эти отдельные отношения правдоподобия перемножают и получают выражение, которое также называется отношением правдоподобия, но уже для всей совокупности наблюдений. Теперь назначается число, называемое порогом, и правило принятия или отвержения гипотезы Н0 состоит в сравнении полученного отношения правдоподобия с порогом: если оно больше порога, принимается гипотеза Н0 («левая» кривая), в противном случае принимается гипотеза H1 («правая» кривая).
Может быть…
Казалось бы, в математической статистике должны быть разработаны методы для назначения или вычисления допустимых вероятностей ошибок при проверке гипотез (критерия α). Однако я должен огорчить вас; эти вопросы лежат не только вне математической статистики, но пока вообще вне математической науки. Хочу обратить ваше внимание на крайнюю субъективность допустимого уровня риска.
Компромисс
В этой ситуации имеется возможность поставить задачу оптимизации: при заданном уровне значимости α выбрать процедуру принятия решения, при которой вероятность ошибки второго рода β будет наименьшей. Сформулированный принцип выбора оптимальной процедуры составляет центральную идею одного из методов статистической проверки гипотез, развитого выдающимися статистиками Джоном Нейманом и Эгоном Пирсоном в середине тридцатых годов XX в.
В теории Неймана–Пирсона критикуется прежде всего достаточно произвольный выбор одной из двух альтернативных гипотез, который царил в статистике до их теории. Однако разработанная ими теория переносит этот произвол на выбор допустимого уровня значимости. Конечно, после того как уровень значимости выбран, проверка гипотез производится со всей научной строгостью. Но значительный произвол все равно остается, он просто перенесен глубже, и теперь труднее обнаружить, сколь велики последствия такого произвола. И сейчас, после интенсивных исследований последних десятилетий, теория статистической проверки гипотез все еще далека от завершения.
Риск
Школьник едет за город на автобусе. Билет стоит 50 коп., и мальчик-сладкоежка подсчитывает, сколько смог бы он купить мороженого на эту сумму. Школьник решает ехать без билета. Конечно, безбилетника может обнаружить контролер. Возможны два исхода эксперимента: ω0 – контролер есть, ω1 – контролера нет, причем Р(ω0) = р – вероятность появления контролера, P(ω1) = 1 – p = q – вероятность непоявления контролера. Школьник может принять два решения: d0 – покупает билет, d1 – едет без билета. Возможные потери школьника: r0 – стоимость билета, r1 – величина штрафа за безбилетный проезд.
Обозначим через L(ωi, di) потери в случае, когда принято решение di, а наступает исход ωi.
Мерилом обсуждаемых средних потерь служит их математическое ожидание при выбранном решении d, так что нас интересует величина
![]()
где – знак математического ожидания.
Она и называется риском при принятии решения d. Вычислим риск при обоих возможных решениях школьника. Если он выбирает решение d0, то есть покупает билет, то
![]()
Это естественно: если билет куплен, то появляется ли контролер или нет, потери школьника — это стоимость билета.
Если же школьник едет без билета, то
![]()
Если вероятность появления контролера р = 0,05, то есть контролер посещает в среднем каждый двадцатый автобус, а величина штрафа 3 рубля, то риск безбилетника
![]()
Выгодно ехать без билета.
Борьба с безбилетниками иногда активизируется – объявляется кампания за «обилечивание» пассажиров. Во время кампании вероятность появления контролера становится равной 0,6, причем пассажиру заранее неизвестно, началась ли кампания или нет. Допустим вероятность обычной автобусной жизни равна g, а вероятность кампании за «обилечивание» = 1 – g. Эти вероятности называют априорными: они известны или, скорее, предполагаются известными до проводимых наблюдений. Знание априорных вероятностей дает возможность вычислить математическое ожидание — риск, то есть взять риск, усредненный по априорным вероятностям.
Таким образом, средний риск для потенциального безбилетника, когда он едет в автобусе, будет равен
![]()
Риск, усредненный по априорным вероятностям, а вслед за ним и решение, доставляющее минимум среднего риска, называют байесовским.
Байесовский подход широко применяется в теории решений. Но здесь есть одно весьма уязвимое место: нужно знать априорные вероятности. Есть ситуации, когда априорные вероятности можно считать известными, например в задачах контроля качества продукции при установившейся технологии массового производства или в некоторых задачах медицинской диагностики. Но, к сожалению, есть много реальных ситуаций, где априорные вероятности не только неизвестны, но и вообще не имеют смысла. Скажем, в задачах обнаружения в системе ПВО не имеет смысла говорить об априорной вероятности появления самолета противника в данном районе. Поэтому при отсутствии априорных вероятностей или при значительных затруднениях с их заданием приходится отказываться от байесовского подхода и вернуться к методу отношения правдоподобия или теории Неймана – Пирсона.
Стратегия разборчивой невесты
Каждая девушка среди своих поклонников ищет Принца и, сопоставляя возможности с желаниями, старается «не промахнуться» выбрать лучшего. Оставим за рамками определение, что есть лучший, и разберем простую математическую модель. Пусть у красавицы имеется n женихов, и она знакомится с ними последовательно. После знакомства она может отвергнуть его или назвать своим избранником. Вернуться к ранее отверженному жениху нельзя, а количество женихов заранее известно и фиксировано (см. также Задача о разборчивой невесте).
Можно остановиться на первом же шаге, то есть выбрать точку с координатой а1. При такой стратегии невеста получает лучшего из претендентов лишь с вероятностью 1/n. Если претендентов много – n велико, – то вероятность выйти замуж за лучшего оказывается весьма маленькой. Однако, есть стратегии и получше.
Пусть n четное. Выберем такую стратегию: пропустим первые n/2 точек, а затем выберем первую точку, координата которой окажется больше всех предыдущих. Вероятность остановиться на точке с наибольшей координатой при этой стратегии будет > 0,25 независимо от величины n.
В общем случае, так как число n всех точек фиксировано, имеется оптимальная стратегия, приводящая к успеху с наибольшей возможной вероятностью. Такая стратегия оптимального выбора состоит в следующем: пропускается некоторое определенное количество объектов s и затем выбирается первый объект, лучший всех предыдущих. Если n очень велико, то оптимальная стратегия позволяет выбрать наилучшего из всех возможных кандидатов с вероятностью:
![]()
где е — основание натуральных логарифмов.
Регрессия
Пусть есть две случайные величины ξ и η, между которыми есть некоторая зависимость: похоже, что чем большее значение х принимает ξ, тем большее значение у принимает ξ. При этом точная зависимость η от ξ не известна. Или, другими словами, зависимость между случайными величинами не детерминированная, а статистическая. Если нарисовать облако данных, соответствующее реализациям случайных величин (ξ, η), то есть наблюденным парам значений — точкам (хi, уi), i = 1, 2, …, n, то они располагаются вдоль какой-то кривой:

Рис. 3. Облако данных двух случайных величин ξ и η
Слово регрессия в статистику ввел Френсис Гальтон, один из создателей математической статистики. Сопоставляя рост детей и их родителей, он обнаружил, что соответствие между ростом отцов и детей слабо выражено, оно оказалось меньшим, чем он ожидал. Однако Гальтон не унывал — он объяснил это явление наследственностью не только от родителей, но и от более отдаленных предков: по его предположениям, то есть по его математической модели, рост определяется наполовину родителями, на четверть — дедом и бабкой, на одну восьмую — прадедом и прабабкой и т.д. Гальтон обратил внимание на движение назад по генеалогическому дереву и назвал это явление регрессией (антоним прогрессу). Впоследствии слово «регрессия» заняло в статистике заметное место, хотя, как это часто бывает в любом языке, в том числе и в языке науки, в него теперь вкладывают другой смысл — оно означает статистическую связь между случайными величинами.
На практике мы почти никогда не знаем точный вид распределения, которому подчиняется величина, а тем более вид совместного распределения двух или большего количества случайных величин, и поэтому уравнение регрессии y = φ(x) нам тоже неизвестно.
Если связь между случайными величинами линейная, зависимость можно записать в виде:
![]()
где β0 и β1 – коэффициенты, которые нужно определить по экспериментальным данным, а ε — ошибка, которую мы полагаем случайной, имеющей нулевое математическое ожидание и такой, что ее значения в различных точках (xi, уi) будут независимыми.
Кирпичики
Если через экспериментальные точки провести кривую и отложить δ-окрестность, то, как бы сложно (угловато, с резкими колебаниями, подъемами или спадами) ни была устроена непрерывная функция, и какое бы маленькое δ мы бы ни выбрали, найдется многочлен, не отличимый с точностью до δ от этой конкретной непрерывной функции. Это утверждение – одна из самых фундаментальных теорем математического анализа; оно носит название теоремы Вейерштрасса об аппроксимации (приближении) непрерывных функций многочленами.
![]()
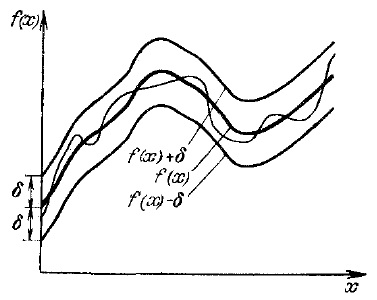
Рис. 4. Регрессионная кривая с δ-окрестностью
Карл Вейерштрасс (1815–1897) – один из наиболее крупных математиков девятнадцатого века. Он получил фундаментальные результаты почти во всех разделах математического анализа.
В строительстве используется набор типовых деталей. В математике многочлены выполняют роль кирпичиков, из которых можно сложить функции, приближающие произвольную непрерывную функцию с любой заданной точностью.
Солнце всходит и заходит…
Любую непрерывную периодическую функцию можно с любой степенью точности приблизить тригонометрическим многочленом:
![]()
Например, кардиограмму:
![]()
Рис. 5. Кардиограмма, как пример периодической непрерывной функции
Вернемся к облаку данных на рис. 3. Уравнение регрессии у=φ(х) нам неизвестно, и из экспериментального материала, независимо от обширности данных, нельзя его вывести. Сначала нужно выдвинуть гипотезу о виде зависимости или, говоря другими словами, выдумать математическую модель и лишь затем, пользуясь экспериментальными данными, проверять ее адекватность.
Самая близкая
Когда выбран вид математической модели, следующим этапом нужно подобрать коэффициенты. Например, для облака экспериментальных данных на рис. 3, выражающих неизвестную нам связь переменных х и у, кажется целесообразным попробовать модель в виде многочлена третьей степени:
![]()
где коэффициенты ai – числа, которые мы и должны отыскать, или, говоря точнее, на основании имеющихся экспериментальных данных вычислить, их оценки – приближенные значения.
Конечно, можно провести целое семейство кривых – графиков подобных многочленов, которые достаточно хорошо будут соответствовать экспериментальному облаку на рис. 3. Ниже нарисованы такие графики. Разбросы же, наглядно изображаемые облаком на рисунке, естественно, считать результатом случая.
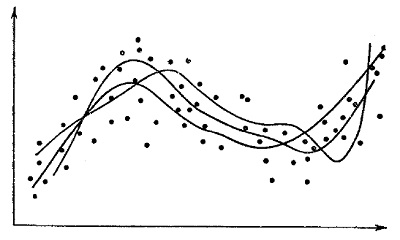
Рис. 6. Несколько вариантов кривых, аппроксимирующих облако данных
Функция f(x), которую мы хотим воспроизвести, нам неизвестна. Вся имеющаяся о ней информация содержится в облаке экспериментальных данных и тех соображениях, на основании которых выбрана математическая модель.
Если начертить график одной из возможных реализаций математической модели выбранного нами вида, то есть при каких-то определенных числовых значениях коэффициентов, то кривая как-то пройдет среди точек экспериментального облака. Соединим теперь каждую экспериментальную точку с кривой посредством отрезка прямой, параллельной оси ординат:
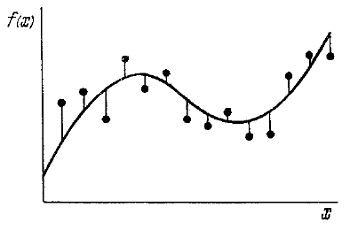
Рис. 7. Метод наименьших квадратов
Самой удобной мерой оценки близости регрессионной кривой к экспериментальным точкам оказалась сумма квадратов длин отрезков. Следует выбрать ту модель (ту кривую), для которой сумма квадратов длин отрезков будет минимальной.
Пороки пассивности
Наблюдение за движением кометы, за течением технологического процесса в режиме нормальной эксплуатации, за достижениями спортсмена – это примеры пассивных экспериментов. Опираясь на данные пассивного эксперимента, можно построить уравнения регрессии и, возможно предсказание значений функций отклика по уравнению регрессии внутри обследуемой области. Восстановление значений функции внутри обследуемой области по отдельным данным, взятым в некоторых точках области, называется интерполяцией. Но часто исследователю нужно знать поведение функции отклика вне обследуемой области, т.е. экстраполировать значения функции. Можно ли воспользоваться уравнением регрессии для решения задачи экстраполяции?
В 1676 году Роберт Гук объявил об открытии закона, устанавливающего связь между удлинением пружины при растяжении и действующей (растягивающей) силой.
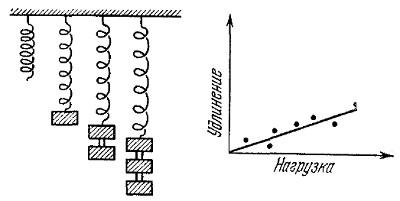
Рис. 8. Схема и результаты эксперимента Гука
Но можно ли предсказать поведение функции отклика и дальше, вне участка нагрузок, проверенных экспериментально, продолжив прямую линию? Пожалуй, сомнительна такая возможность. И в самом деле, как показывают дальнейшие эксперименты, начиная с некоторых значений нагрузки, линейность нарушается, а затем нарушается и упругость. Этот пример иллюстрирует небезопасность экстраполяции.
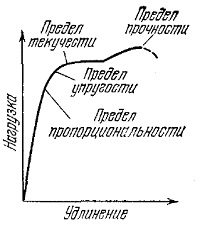
Рис. 9. Зависимость удлинения от нагрузки в более широком диапазоне
Активный против пассивного
В условиях активного эксперимента исследователь имеет возможность в факторном пространстве сам выбирать точки, в которых будут ставиться эксперименты. Отобранные точки в факторном пространстве и последовательность, в которой ставятся эксперименты в выбранных точках, называют планом эксперимента, и поэтому выбор точек и стратегии их последовательного использования— это и есть планирование эксперимента.
Шаг за шагом
Выделим на поверхности отклика какую-то точку и рассмотрим небольшую ее окрестность. В малой окрестности кусок достаточно гладкой поверхности практически не отличим от куска плоскости, и если плоскость не параллельна горизонтальной плоскости, то по ней можно сделать шаг вниз по наиболее крутому направлению. Перейдя в новую точку и выделив ее небольшую окрестность, можно опять построить кусок плоскости, практически неотличимый от куска поверхности, и сделать вновь наиболее крутой шаг вниз. Так будет продолжаться движение вниз до тех пор, пока либо не будет достигнута граница допустимой области, либо в окрестности точки плоскость окажется параллельной горизонтальной плоскости.
Предлагаемая шаговая или последовательная стратегия эксперимента представляет собой вариант последовательного анализа Вальда, где для проверки гипотезы (о стационарности точки, о наличии минимума, о глобальности этого минимума) производятся эксперименты.
Где ставить эксперименты?
Рассмотрим задачу взвешивания трех образцов. Можно последовательно взвешивать каждый из них. Так и поступает традиционный исследователь, но вначале он делает холостое взвешивание для определения нулевой точки весов. Когда образец кладется на весы, в таблице ставится +1, когда он на весах отсутствует — ставится -1. Результат взвешивания обозначим через у с соответствующим индексом:
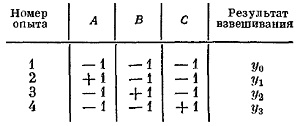
Рис. 10. Традиционная схема взвешивания трех образцов
Исследователь изучает поведение каждого фактора в отдельности, то есть проводит однофакторные эксперименты. Вес каждого из образцов оценивается лишь по результатам двух опытов: холостого опыта и того, в котором изучаемый объект был на весах. Например, вес образца А:
![]()
Ошибка взвешивания предполагается независимой от взвешиваемой величины, аддитивной и имеющей одно и то же распределение. Тогда дисперсия измерения веса образца:
![]()
где σ2 – дисперсия любого взвешивания.
Такой же будет дисперсия веса образцов В и С.
Но эксперимент можно провести и по другому плану — многофакторному:
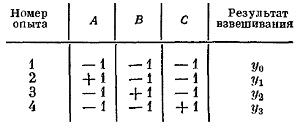
Рис. 11. Многофакторный план взвешивания трех образцов
Теперь нет холостого взвешивания. В первых трех опытах последовательно взвешивают образцы А, В, С, а в четвертом взвешиваются все три образца вместе. Умножая элементы последнего столбца таблицы последовательно на элементы столбцов А, В, С и деля на два, ибо, в соответствии с планом, каждый из образцов взвешивается дважды, получим веса:
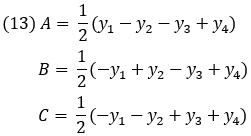
Здесь веса образцов не искажаются весами других, ибо, например, в выражение для веса образца В каждый из весов образцов А и С входит дважды и притом с разными знаками. Дисперсия ошибки взвешивания теперь равна
![]()
то есть вдвое меньше, чем при однофакторном плане взвешивания. Если бы мы захотели при однофакторном плане получить такую же дисперсию, как и при обсуждаемом многофакторном, то следовало бы провести каждый из четырех однофакторных опытов дважды, то есть провести восемь взвешиваний вместо четырех.
Итак, при многофакторном плане каждый вес вычисляется по результатам всех четырех опытов — вот причина уменьшения дисперсии вдвое! (О дробном факторном эксперименте и его плане см. Юрий Адлер. Введение в планирование эксперимента.)
Теория планирования эксперимента началась с работ знаменитого английского статистика сэра Рональда Фишера в 20–30-х годах XX века и затем, в рассматриваемом направлении, была развита в пятидесятых годах в США Дж. Боксом и его сотрудниками, и именно эти последние работы, имевшие четко выраженный прикладной характер, стимулировали их широкое признание.
Как достичь успеха
Если исследуются не количественные факторы, а качественные, то используется дисперсионный анализ (см. например, Однофакторный дисперсионный анализ и Двухфакторный дисперсионный анализ). Дисперсионный анализ широко применяется в психологии, биологии, химии — всюду, где встречаются задачи с качественными факторами.
Реплики под занавес
В теории эксперимента главное достижение вовсе не в сокращении числа необходимых опытов. Сознательное планирование эксперимента влечет за собой необходимость четкого логического анализа всей ситуации от продумывания исходных посылок, анализа априорной информации и выбора адекватной модели до использования рандомизации, последовательной стратегии эксперимента, оптимального выбора точек в факторном пространстве, разумной, обоснованной интерпретации результатов статистической обработки, причем представленной в компактной форме, удобной и для публикации, и для дальнейшего использования.