В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель — это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения. [1]
Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.
Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.
- Выборка состоит из фиксированного числа элементов n, представляющих собой исходы некоего испытания.
- Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача.
- Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 – р.
- Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.
Скачать заметку в формате Word или pdf, примеры в формате Excel2207
Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.
Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.
Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:
Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:
Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009. Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей n элементов, следует воспользоваться формулой сочетаний (1):
где n! = n * (n –1) * (n – 2) * … * 2 * 1 — факториал числа n, причем 0! = 1 и 1! = 1 по определению.
Это выражение часто обозначают как ![]() . Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:
. Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:
Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:
(Количество возможных последовательностей) *
(вероятность конкретной последовательности) = 4 * 0,0009 = 0,0036
Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.
Биномиальное распределение
где Р(Х) — вероятность X успехов при заданных объеме выборки n и вероятности успеха р, X = 0, 1, … n.
Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X, подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n. Произведение рX(1 – р)n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n. Величина ![]() определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях. Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна
определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях. Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна
Р(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =![]()
Рассмотрим примеры, иллюстрирующие применение формулы (2).
1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна
2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна
Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна
Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037
3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события
Р(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
Используя формулу (2), вычислим каждую из этих вероятностей:
Следовательно, Р(Х < 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
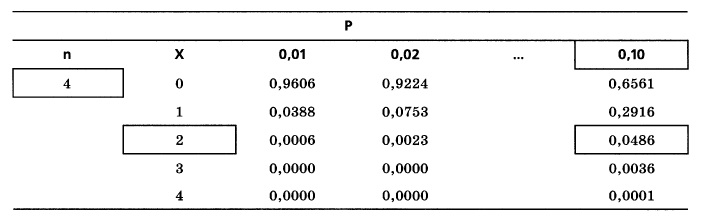
По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее. Некоторые из этих вероятностей приведены рис. 1. Например, чтобы получить вероятность, что Х = 2 при n = 4 и p = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0,1.
Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1
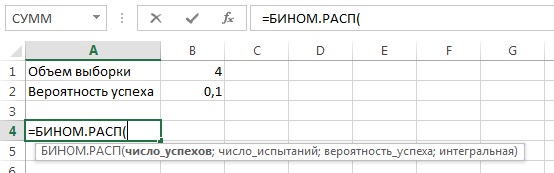
Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х, число испытаний (или объем выборки) – n, вероятность успеха – р, параметр интегральная, принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).
Рис. 2. Параметры функции =БИНОМ.РАСП()
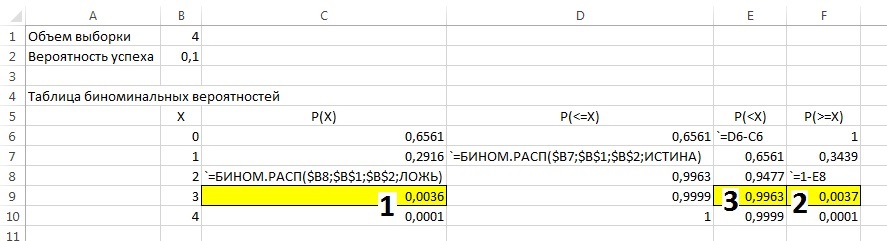
Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле. Цифрами показаны ответы на примеры соответствующего номера).
Рис. 3. Расчет биномиального распределения в Excel для n = 4 и p = 0,1
Свойства биномиального распределения
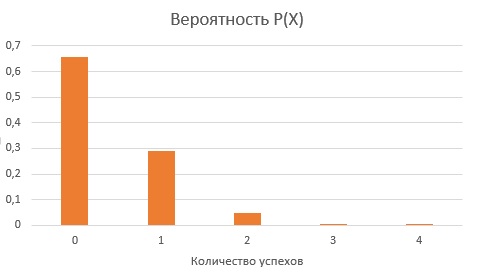
Биномиальное распределение зависит от параметров n и р. Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,5, биномиальное распределение является симметричным независимо от величины параметра n. Однако, если р ≠ 0,5, распределение становится асимметричным. Чем ближе значение параметра р к 0,5 и чем больше объем выборки n, тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).
Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1
Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р:
(3) Μ = Е(Х) = np
В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.
Стандартное отклонение биномиального распределения
Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:
Предыдущая заметка Ковариация и ее применение в финансовом деле
Следующая заметка Гипергеометрическое распределение
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313
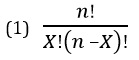
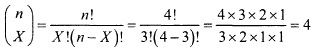
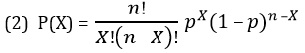
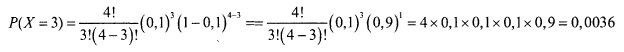
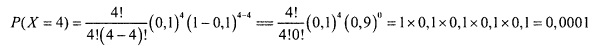
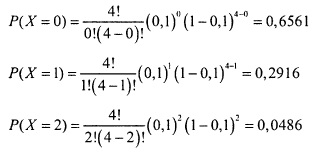
Здравствуйте, мне 23 года, я учусь в Европе и уже заканчиваю университет подготовкой к ГОСам.
Вы очень помогли мне понять тему распределений в статистике, очень много материала перечитал, но ваш изложен наиболее лаконично.
Спасибо огромное!
Здравствуйте, г-н Багузин.
Я исследую распределение наночастиц по размеру.
Распределение наночастиц имеет вид несимметричной кривой с максимумом в диапазоне 2-4 нм в координатах «Относит. частота наблюдения частиц — размер частиц (от 0.5 до 10 нм). Величина максимума обычно колеблется от 10 до 15%.
Какая модель будет лучше описывать распределение частиц, по Вашему мнению?
Насколько корректно рассчитать объем и поверхность таких сферических частиц путем интегрирования наблюдаемой в микроскопе
функции распределения частиц?
Валентин, задача подбора функции распределения по экспериментальным данным довольно сложна… и на мой взгляд, однозначного решения вы не найдете. Как правило идут от какой-то теории. Теория подразумевает какое-то распределение, и вы подбираете параметры распределения, чтобы добиться наилучшей корреляции теоретической кривой и экспериментальных данных. Несимметричную кривую дает целый ряд распределений: биномиальное, гипергеометрическое, хи-квадрат, …