Увлекательное введение в науку о данных, в котором упор делается на критическое мышление, а не на статистические методы. Введение в науку о данных или статистику не должно начинаться с доказательства сложных теорем или запоминания терминов и формул, но именно так устроены многие учебники по статистике. В книге показано, как инструменты критического анализа применяются к проблемам в самых разных областях, включая выборы, гражданские конфликты, преступность, терроризм, финансовые кризисы, здравоохранение, спорт, музыка и космические путешествия.
Итан Мескита, Энтони Фаулер. Статистика без подвоха. Методы критического анализа данных и причинного вывода. М.: ДМК Пресс, 2023. – 454 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 4% от объема книги)
Купить бумажную или цифровую книгу в издательстве ДМК-Пресс, бумажную книгу в Ozon или Лабиринте
Глава 1. Критическое мышление в эпоху данных
Тот факт, что аргумент опирается на сложный количественный анализ данных, не означает, что этот аргумент строгий или правильный. Чтобы использовать возможности данных для принятия более эффективных решений, мы должны сочетать количественный анализ с критическим мышлением.
Как получается, что эксперты в столь многих областях так часто допускают существенные ошибки? Экспертное знание в любой области приходит в результате обучения, практики и опыта. Но никто не прикладывает аналогичные усилия, чтобы научиться корректно и непредвзято работать с данными. И даже когда люди стремятся к этому, их преподаватели склонны преувеличивать технические аспекты и недооценивать концептуальные, хотя фундаментальные проблемы почти всегда связаны с концептуальными ошибками в мышлении, а не с техническими ошибками в расчетах.
Глава 2. Корреляция: что это такое и для чего она нужна?
Корреляция между двумя явлениями мира – это степень, в которой они склонны происходить вместе. Чтобы оценить корреляцию, нам нужны вариации обеих переменных.
Почему корреляции самый важный инструмент количественного анализа? Потому что корреляция позволяет нам предсказать изменение какого-либо показателя или свойства на основании известных изменений других показателей или свойств.
Существуют три варианта использования такого рода знаний: (1) описание, (2) прогнозирование и (3) причинно-следственная связь. Каждый раз, когда вы собираетесь использовать корреляцию, следует четко понимать, какую из этих трех задач вы пытаетесь решить и какими должны быть достоверные знания о мире, чтобы корреляция была применима в конкретных условиях.
Описание отношений между свойствами или признаками объектов мира – самый простой способ использования корреляций. Если вы хотите делать прогнозы, нужно быть готовым сделать некоторые дополнительные предположения о мире. Во-первых, является ли взаимосвязь, которую вы обнаружили в своей выборке, отражением более широкого явления, или она является результатом случайных изменений в ваших данных? Ответ на этот вопрос требует статистического вывода. Во-вторых, даже если вы убеждены, что обнаружили реальную взаимосвязь в своей выборке, следует подумать о том, является ли ваша выборка репрезентативной для генеральной совокупности, относительно которой вы пытаетесь сделать прогнозы.
В целом неправильно делать вывод о причинно-следственной связи на основе корреляций, хотя многие эксперты занимаются этим постоянно.
Измерение корреляций
Существует несколько разновидностей статистических данных, которые можно использовать для описания и измерения корреляции между переменными: ковариация, коэффициент корреляции и наклон линии регрессии.
Ковариация:
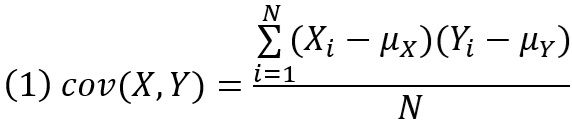
В ковариации произведение отклонений зависит от того, насколько изменчивы переменные. Коэффициент корреляции учитывает дисперсию переменных:
![]()
Коэффициент корреляции принимает значение от –1 до 1. Иногда коэффициент корреляции возводят в квадрат, чтобы вычислить показатель r2. Его значение всегда находится между 0 и 1. r2 часто интерпретируют как долю изменчивости Y, объясняемую X.
Одна из потенциальных проблем, связанных с коэффициентом корреляции и показателем r2, заключается в том, что они ничего не говорят о размере связи между Х и Y. Поэтому часто используют наклон линии наилучшего соответствия. Она же линия регрессии наименьших квадратов (ordinary least squares, OLS). Наклон линии регрессии (также иногда называемый коэффициентом регрессии), когда значение Y находится на вертикальной оси, а X – на горизонтальной оси, равен
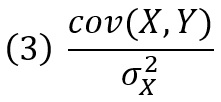
Это число наглядно показывает нам, насколько в среднем изменяется Y при увеличении X на одну единицу.
Линейные связи интересны и важны, но не все связи линейны. Рассмотрим две возможные связи между переменными Х и Y:
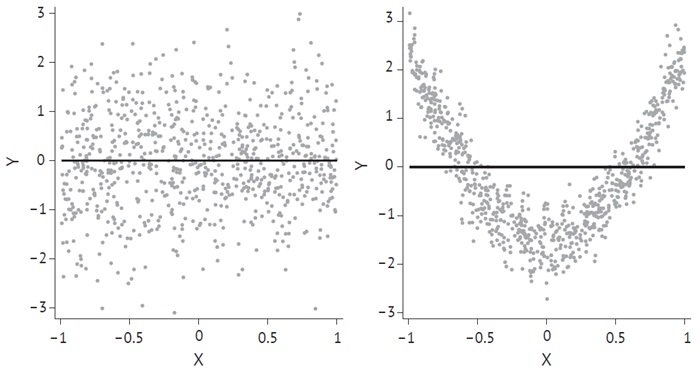
Рис. 1. Нулевая корреляция может означать многое
На левом графике нет корреляции между X и Y, а также, похоже, нет каких-либо интересных отношений. На правом графике также нет корреляции между Х и У – в среднем более высокие значения X не обязательно связаны с высокими значениями Y, а низкие значения X не имеют тенденции возникать вместе с низкими значениями Y. Но между этими двумя переменными существует связь. Переменная X на правом графике полезна для прогнозирования Y. Рациональный анализ данных требует большего, чем просто вычисление корреляций. Важно смотреть на данные с разных точек зрения (например, с помощью диаграмм рассеяния, подобных этой).
Глава 3. Причинно-следственная связь: что это такое и для чего она нужна?
«Какое влияние это оказало на результат?» – более концептуально правильный вопрос, чем «Что стало причиной явления?»
Причинный эффект – это изменение какой-либо характеристики мира вследствие изменения другой его характеристики. Так, например, можно сказать, что ставка налога оказывает причинное влияние на государственные доходы.
Мы дали весьма свободное разговорное определение причинного эффекта, поэтому вы, возможно, не заметили, что мы немного коснулись философии. Что подразумевается под следствием или результатом? Ведь мир такой, какой он есть. Откуда взялось это изменение какой-то другой характеристики мира?
Фактически наше определение причинно-следственной связи основано на мысленном эксперименте. Подобные сравнения называются контрфактическими (counterfactual) мысленными экспериментами, потому что по крайней мере один из миров, которые мы сравниваем, не является реальным, фактическим миром – он находится в нашем воображении. Сравнение результатов такого мысленного эксперимента является контрфактическим сравнением.
Теперь становится ясно, что, говоря о «следствии» или «результате», мы на самом деле имеем в виду определение причинно-следственной связи. Мы говорим о сравнении между результатом в реальном мире и результатом в контрфактическом мире. Идея контрфактуальности философски тонка. Мы введем математический механизм описания контрфактических явлений, называемых потенциальными исходами (potential outcome).
Для каждого человека мы можем наблюдать только один потенциальный исход. Но причинно-следственное явление – это разница в потенциальных исходах для одного человека. Эта присущая причинным явлениям принципиальная ненаблюдаемость называется фундаментальной проблемой причинного вывода.
Влияние поступления в колледж на ваш доход – это разница в ваших доходах в мире, в котором вы учитесь в колледже, и в мире, в котором вы не учитесь в колледже. Вы не можете одновременно поступить и не поступить. То есть у вас есть два потенциальных результата. Но реальный исход у вас только один.
Но как добиться ответов на причинно-следственные вопросы, если последствия воздействия принципиально ненаблюдаемы? К счастью, существует множество ситуаций, когда нам не обязательно знать эффект для каждого отдельного объекта анализа. Вместо этого достаточно знать средний эффект для многих людей.
В чем причина?
Расхожее утверждение гласит, что Первая мировая война была вызвана убийством в 1914 г. эрцгерцога Фердинанда, наследника престола Австро-Венгрии (см., например, Барбара Такман. Августовские пушки). Убийцы были частью движения, которое хотело, чтобы Сербия взяла под свой контроль Южные Балканы, включая Боснию и Герцеговину, которые Австро-Венгрия аннексировала в 1908 г. Правительство Австро-Венгрии ответило на убийство июльским ультиматумом. Условия ультиматума были настолько обременительны, что сербское правительство их отвергло. Когда ультиматум был отклонен, Австро-Венгрия объявила войну Сербии, что побудило Россию мобилизовать свою армию для защиты Сербии. В ответ Германия (союзница Австро-Венгрии) объявила войну России, Франция (союзница России) объявила войну Германии, и вся эта неразбериха переросла в Первую мировую войну. Поэтому принято говорить, что убийство эрцгерцога Фердинанда вызвало Первую мировую войну.
Применим к этому утверждению контрфактический подход. Можно задаться вопросом: случилась бы Первая мировая война в контрфактическом мире, в котором Фердинанд не был убит? Если бы в этом контрфактическом мире Первая мировая война не началась, то было бы правильно сказать, что убийство повлияло на начало войны. Но это далеко не утверждение, что убийство эрцгерцога стало причиной войны. Ведь существует множество факторов, которые, будь они иными, предотвратили бы начало Первой мировой войны. Конечно, если бы эрцгерцог Фердинанд не был убит, возможно, война (в том виде, как мы ее знаем из истории) не началась бы. Но кроме того, если бы Австро-Венгрия не аннексировала Боснию и Герцеговину, возможно, Фердинанд никогда бы не был убит и война никогда бы не началась, поэтому аннексия была такой же причиной, как и убийство. Точно так же, если бы сербское правительство приняло июльский ультиматум, возможно, войны удалось бы избежать, поэтому несоблюдение ультиматума также было причиной.
Еще одно удивительное следствие контрфактического подхода заключается в том, что некоторые события могут вообще не иметь причин. Некоторые события могут быть результатом совпадения нескольких факторов, при этом наличие или отсутствие отдельного фактора не способно изменить исход. Эта теоретическая возможность является еще одной причиной того, что, возможно, не имеет особого смысла задавать вопросы типа «Что стало причиной Первой мировой войны?». Вполне возможно, что, несмотря на все факторы, о которых мы любим говорить, устранения любого из них на самом деле было бы недостаточно для предотвращения войны.
Мы пришли к убеждению, что корреляция не обязательно подразумевает причинно-следственную связь. Но, что, возможно, еще более удивительно, причинно-следственная связь не обязательно подразумевает корреляцию.
Глава 4. Не бывает корреляции без вариаций
Вы не можете узнать о корреляции без изменения обеих интересующих переменных. Неспособность найти вариацию той или иной переменной при попытке установить корреляцию является исключительно распространенной ошибкой. Первая причина заключается в выборе зависимой переменной. Вторая – в том, что мир часто устроен таким образом, что подталкивает нас совершать эту ошибку.
Если вы хотите спрогнозировать или объяснить какое-то явление, естественным побуждением будет начать с изучения предыдущих случаев возникновения этого явления. Это называется выбором зависимой переменной. Но если вы смотрите только на случаи, когда явление имело место, вы пытаетесь оценить корреляцию без вариаций, поскольку у вас нет различий в том, произошло это явление или нет.
В 2006 г. Фонд Билла и Мелинды Гейтс заказал исследование причин прекращения учебы в средней школе. Почти половина (47%) прервавших обучение заявили, что основной причиной ухода из школы были неинтересные занятия. 69% респондентов заявили, что у них нет мотивации или вдохновения усердно работать.
Однако, тот факт, что половина бросивших школу считает учебу скучной, не означает, что скучность школы коррелирует с уходом из нее. Поскольку корреляция требует вариаций, ее измерение должно включать сравнение тех, кто бросил школу, с теми, кто не бросил, чтобы увидеть, насколько велика доля бросивших школу среди тех, кто считает учебу скучной. Исследование Фонда Гейтса, поскольку оно рассматривает только тех, кто бросил школу, не может провести такое сравнение.
Эта же проблема свойственна процессу расследования после катастроф. Мы склонны смотреть на факторы, которые, как нам кажется, способствовали катастрофе, спрашивать, присутствовали ли они и в прошлых катастрофах, и, если это так, приходить к выводу, что нам следует устранить эти факторы в будущем. Но без анализа всех ситуаций, включая те, в которых катастрофы не было, мы не можем на самом деле узнать, коррелирует ли наличие этих факторов с возникновением катастрофы. Поэтому мы не знаем, есть ли чему поучиться.
Глава 5. Применение регрессии в описании и прогнозировании
Наши прогнозы становятся все лучше и лучше по мере того, как мы включаем все больше и больше объясняющих переменных, поскольку у нас появляется все больше и больше параметров, с которыми мы можем экспериментировать, чтобы настроить кривую на соответствие данным. Но это не обязательно означает, что вы должны использовать как можно больше объясняющих переменных. Нужно искать компромисс.
Прежде всего помните, что частью нашей цели является описание данных в простой и лаконичной форме, которую легко понять и объяснить. Добавление все большего количества членов уравнения часто приводит к ухудшению прогнозов за пределами выборки. Причина в том, что, по мере того как используемая нами функция становится все более и более гибкой, она может начать воспринимать каждый небольшой скачок и сбой в данных как значимый эффект, даже если это не так. Это явление называется переобучением (overfitting).
По сравнению с большинством сложных политических явлений президентские выборы в США довольно предсказуемы. Даже за несколько месяцев до выборов мы часто имеем довольно хорошее представление о том, кто победит, исходя из состояния экономики. А в последние недели перед днем выборов среднее значение опросов обычно находится в пределах одного или двух процентных пунктов от окончательной доли голосов. Журналист Нейт Сильвер зарекомендовал себя как гигант в области анализа политических данных, по сути, усредняя результаты опросов (подробнее см. Нейт Сильвер. Сигнал и шум).
Один из способов попытаться оценить и смягчить переобучение – исключить некоторые данные из вашего регрессионного анализа и провести тесты вне выборки. Можно получить регрессию на 90% ваших данных, и проверить её на оставшихся 10%.
Наиболее распространенной формой представления выводов регрессии является таблица:
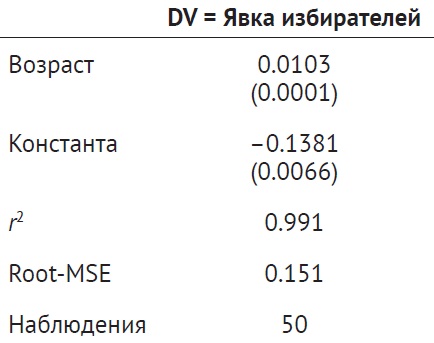
Рис. 2. Вывод регрессии средней явки избирателей по возрасту
Число в скобках – стандартная ошибка. Число в строке «Константа» – это точка пересечения регрессионной кривой с осью 0Y – αOLS. Число в строке «Возраст» представляет собой наклон линии регрессии βOLS. r2 – величина отклонения в явке избирателей, которую можно предсказать по возрасту. Root-MSE – это квадратный корень из среднеквадратической ошибки, который дает вам некоторое представление о том, насколько в среднем прогнозы регрессии далеки от реальных точек данных.
Глава 6. Выборки, неопределенность и статистические выводы
Оценка = Оцениваемая величина + Смещение + Шум
Оценка (estimate) – это число, которое мы получаем в результате анализа выборки. Мы надеемся, что наша оценка будет близка к истинному значению переменной в генеральной совокупности, которое мы называем оцениваемой величиной (estimand). Оценка может не совпадать с оцениваемой величиной по двум причинам: из-за систематической ошибки или смещения (bias) и шума. Смещение относится к ошибкам, которые происходят по систематическим причинам, а шум относится к нефакторным (несистематическим) ошибкам, возникающим по случайным причинам.
Мы говорим, что оценивающий процесс является несмещенным, если после его применения к бесконечному числу новых независимых выборок среднее значение генерируемых им оценок будет равно оцениваемой величине (подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?).
Стандартное отклонение – способ измерения того, насколько широко простирается распределение переменной (или, что аналогично, насколько изменчивой является переменная). Представьте, что мы запустили наш оцениватель бесконечное количество раз, каждый раз с новой выборкой данных. В этом мысленном эксперименте мы можем рассматривать саму оценку как переменную. Каждый раз, когда мы извлекаем выборку данных и запускаем оцениватель, мы получаем другое значение оценки из-за шума. Следовательно, можно представить распределение оценок, которые мы получим после повторения нашей оценки бесконечное количество раз. Это воображаемое распределение называется выборочным распределением (sampling distribution)[1]. Стандартное отклонение этого выборочного распределения называется стандартной ошибкой (standard error). Стандартная ошибка, если бы мы ее знали, дала бы нам представление о том, насколько далека любая конкретная оценка от средней оценки, поскольку она измеряет, насколько изменчивыми будут наши оценки. Если оценка не смещена, средняя оценка равна оцениваемой величине. Для несмещенной оценки стандартная ошибка приблизительно говорит нам, насколько далека типичная оценка от истинного значения, которое мы пытаемся узнать.
Стандартная ошибка примерно равна
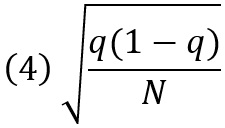
где N обозначает размер выборки, q – вероятность «да», (1–q) – вероятность «нет».
Но мы не знаем q. На практике мы аппроксимируем стандартную ошибку, подставляя в формулу вместо q нашу оценку этой величины, равную выборочному q̂.
Маленькие выборки и экстремальные наблюдения
Маленькие города, как правило, доминируют в списке мест с экстремальным уровнем заболеваемости раком или средними доходами не потому, что они обязательно в среднем более или менее предрасположены к раку или более или менее богаты, а потому, что уровень заболеваемости раком и средние доходы в них более изменчивы, чем в местах с более высоким количеством людей для усреднения.
Статистический вывод и проверка гипотез
Как делать выводы о генеральных совокупностях, используя оценки на основе выборок? Для этого нам нужно прибегнуть к проверке гипотезы. Предположим, мы провели беспристрастный опрос тысячи избирателей, и это дало оценку доли голосов кандидата от республиканской партии в q = 0,532, или 53,2%. Насколько вероятно, что мы могли бы наблюдать такие свидетельства, даже если республиканец не более популярен, чем демократ. Поэтому мы проверяем, насколько вероятно, что мы бы заметили наблюдаемые доказательства, если бы два кандидата были на самом деле одинаково популярны. Этот эталон отсутствия отношений обычно называют нулевой гипотезой.
Чтобы понять суть проверки гипотезы, начнем с предположения, что нулевая гипотеза верна, т.е. два кандидата одинаково популярны, поэтому q = 0,5. Теперь зададимся вопросом, насколько вероятно, что мы получим результат опроса, по крайней мере, столь же благоприятный для республиканца, как тот, который мы фактически нашли, (q̂ = 0,532).
При истинной доле голосов q = 0,5 и опросе одной тысячи избирателей стандартная ошибка нашего оценивателя по формуле (4) составляет приблизительно 1,6 процентного пункта
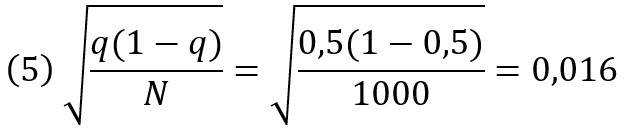
Наша оценка 0,532 соответствует превышению нулевой гипотезы на две стандартные ошибки (0,5 + 2*0,016 = 0,532). Центральная предельная теорема гласит, что 95% оценок из беспристрастного опроса, который мы проводили, будут находиться в пределах двух стандартных ошибок от истинного значения, а это означает, что только 5% оценок будут отклоняться более чем на две стандартные ошибки от истинного значения. Более того, в половине этих неудачных случаев оценка будет на две стандартные ошибки ниже истинного значения (что указывает на заметное лидерство демократа). Таким образом, если нулевая гипотеза верна, вероятность того, что мы получим результат опроса, столь же благоприятный для республиканца, как и тот, который мы получили, составляет около 2,5%, или 1 из 40.
Проверка гипотез – это стратегия оценки вероятности получения столь экстремального результата, как ваш, при условии, что нулевая гипотеза верна.
Статистическая значимость
Полученная выше вероятность 2,5% называется p-значением. Если наше значение p действительно низкое, мы можем заключить, что нулевая гипотеза вряд ли верна. Таким образом, мы располагаем статистически убедительными свидетельствами того, что избиратели действительно отдают предпочтение республиканцам.
Общий подход заключается в том, чтобы заранее указать определенный порог (чаще всего 0,05), и, если значение p ниже этого порога, мы говорим, что отвергаем нулевую гипотезу, и делаем вывод, что у нас есть статистически значимые доказательства в пользу гипотезы, которую мы проверяли. Конечно, проверка гипотез не дает определенных выводов. При пороге значимости 0,05 существует 5%-ная вероятность получения статистически значимого результата, даже если нулевая гипотеза верна. Но проверка гипотез дает один из способов количественного рассуждения о том, может ли закономерность или результат, обнаруженный вами в наборе данных, отражать подлинное явление, а не просто быть следствием шума.
Хотя статистическая значимость полезна и информативна, ее часто неправильно используют и неправильно понимают. Критическое мышление и данные дополняют, а не заменяют друг друга. Тот факт, что мы занимаемся статистикой, не означает, что мы должны перестать предметно думать о вопросах, на которые стремимся ответить. Мы должны использовать статистические выводы, когда это возможно. Но также нужно всегда напоминать себе о необходимости делать существенные выводы на основе имеющихся фактов.
Интересная история о том, как ученые и статистики пришли к общепринятому 5%-ному порогу статистической значимости, изложена в статье: Michael Cowles and Caroline Davis. 1982. On the Origins of the .05 Level of Statistical Significance. American Psychologist 37 (5): 553-58.
История вероятностей и статистики см. Ian Hacking. 2006. The Emergence of Probability: A Philosophical Study of Early Ideas about Probability and Statistical Inference, 2nd Edition. Cambridge University Press и Ian Hacking. 1990. The Taming of Chance. Cambridge University Press.
Глава 7. Завышение значимости и занижение отчетности
Когда мы обнаруживаем закономерности в данных, мы хотим знать, отражают ли они реальные явления или же они могли легко возникнуть в результате случайности. Поэтому статистическая проверка гипотез и p-значения явно полезны. Но есть проблема. Ни общественность, ни более широкое научное сообщество не видят всех проверок гипотез, которые были (или могли быть) проведены. Обычно принято обнародовать только статистически значимые результаты.
Выбор наилучших результатов из большого количества испытаний, т. е. завышение значимости (over-comparing) и избирательное сообщение только об интересных или статистически значимых случаях, т. е. занижение отчетности (under-reporting), – опасная комбинация, которая встречается повсеместно.
Проблема завышения значимости и занижения отчетности влияет на нашу способность накапливать знания в определенной области в течение продолжительного времени. Мы знаем, что любая оценка, даже несмещенная, может быть далека от истинной оценки из-за шума. Есть надежда, что по мере накопления оценок шум усредняется, так что среднее значение большого количества несмещенных оценок становится очень близким к истинной оценке. Завышение значимости и занижение отчетности означает, что этого может не случиться при анализе опубликованных оценок – тревожное явление, называемое предвзятостью публикации (publication bias).
Одна из причин, по которой мы можем столкнуться с завышением значимости и занижением отчетности, – неправильное или нечестное поведение отдельных аналитиков. Научное сообщество называет игру с данными или тестами до тех пор, пока значение p не станет ниже определенного порога, р-хакингом. Допустим, ученый проводит эксперимент и не получает статистически значимых доказательств ожидаемого или желаемого результата. Этот ученый может решить, что, вероятно, что-то было не так с первой попыткой, и поэтому попытается немного подкорректировать эксперимент. Фактически ученый может продолжать проводить подобные эксперименты до тех пор, пока один из них не станет статистически значимым. Если он проведет эксперимент достаточное количество раз, то из-за воздействия шума рано или поздно получит искомый результат, даже если изучаемого явления в реальности не существует. Это проблема завышения значимости отдельного эксперимента. И, конечно, если недобросовестный ученый сообщает только о результатах одного эксперимента, который дал статистически значимый результат, мы сталкиваемся с проблемой занижения отчетности и, следовательно, предвзятости публикации.
Еще один способ завышения значимости – это рассмотреть множество разных эффектов воздействия. Предположим, вы хотите оценить эффективность какой-то новой таблетки от сердечно-сосудистых заболеваний. Вы можете провести отличное клиническое исследование, в данных которого вообще отсутствует предвзятость. Но, возможно, вы собрали данные о многих показателях среди подопытных пациентов: смертности, частоте сердечных приступов и инсультов, уровне холестерина, продолжительности госпитализации, способности заниматься физическими упражнениями, субъективном ощущении здоровья и т.д. Затем вы можете проверить, оказывает ли таблетка статистически значимое влияние на каждый из этих результатов. Если вы рассмотрите достаточно много разных показателей, то, скорее всего, обнаружите статистически значимый результат по одному из них просто из-за шума – т.е. люди, получившие лекарство, и люди, получившие плацебо, будут различаться по некоторым результатам, даже если лекарство вообще ни на что не влияет.
Под р-скринингом мы понимаем эксперименты, которые не дали статистически значимых доказательств эффекта, и не привели к публикации статьи.
Всегда сложно узнать наверняка, применялся ли р-хакинг в отдельном исследовании. Тем не менее критическое мышление помогает нам понять, насколько широко распространена проблема р-хакинга. Наилучшим доказательством этому служит исследование р-значений в опубликованной научной литературе.
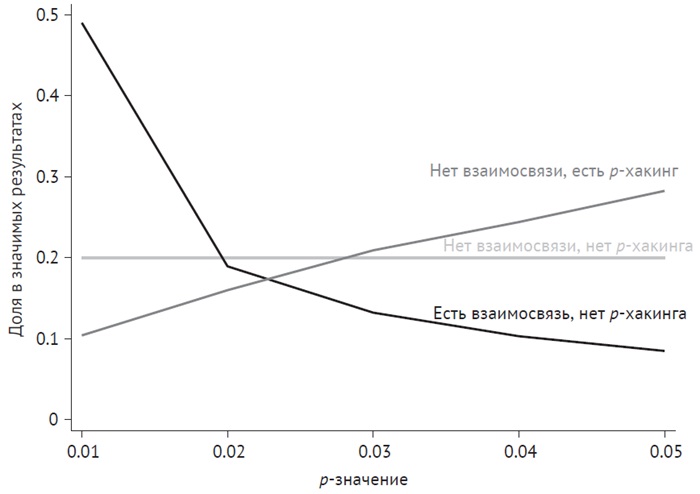
Рис. 3. р-хакинг искажает распределение p-значений в научных публикациях
Порог 0,05 – это произвольное число. Мы должны использовать p-значения, когда это уместно. Но они не являются окончательным средством оценки правдоподобности количественных результатов.
Глава 8. Возврат к среднему значению
У любого показателя, который частично является функцией систематических факторов (иногда их называют сигналом), а частично функцией случайных или несистематических факторов (которые мы иногда называем шумом), произойдет возврат к среднему значению. Представьте себе многократно наблюдаемый исход, где при каждом наблюдении результат отражает комбинацию систематического сигнала (например, генов) и случайного шума (например, солнечного света). Экстремальные результаты обычно возникают из-за совпадения экстремальных значений как сигнала, так и шума. В других итерациях, пока сигнал остается фиксированным, шум принимает новое случайное значение. И ожидаемо значение шума будет средним. Таким образом, ожидается, что экстремальные значения в одной итерации вернутся к среднему значению в других итерациях.
Многие явления в мире имеют подобную структуру «сигнал-шум». Поэтому явление возврата к среднему значению встречается повсеместно. Следовательно, критическое отношение к доказательствам заставляет нас помнить о возможности возврата к среднему значению.
Предположим, вы наблюдаете некоторый результат, состоящий из сигнала и шума, и этот результат на удивление велик. (Этот аргумент, конечно, работает и для удивительно малых значений.) Затем предположим, что вы собираетесь наблюдать другой результат, где сигнал такой же, как и при первом наблюдении, но будет новый, независимый выброс шума. Поскольку первое наблюдение очень велико, оно, вероятно, отражает большую величину сигнала и большую величину шума. Новое наблюдение снова имеет большое значение сигнала, но значение шума, вероятно, будет меньше. Так что новое наблюдение, скорее всего, будет меньше.
Важно отметить, что, приводя этот аргумент, мы ничего не сказали о том, какой результат возник первым во времени. Мы говорили только о порядке, в котором вы их наблюдали. Возврат к среднему значению – это не сила гравитации, которая с течением времени притягивает вещи к среднему значению. Для логики возврата к среднему значению абсолютно не важно, что во времени произошло первым.
Комментаторы, аналитики и случайные наблюдатели из раза в раз неправильно понимают природу возврата к среднему значению, придумывая сложные теории для объяснения закономерностей, отражающих простое статистическое явление. Это звучит так, будто мы должны подозревать возврат к среднему значению почти везде, и в грубом приближении так и есть. Мы должны наблюдать возврат к среднему значению любой переменной, на которую влияют сигнал и шум.
Но есть ситуации, когда нам не следует ожидать возврата к среднему значению. Возьмем, к примеру, фондовый рынок. Стоит ли нам ожидать возврата к среднему значению цен на акции? Из логики возврата к среднему значению следует, что в среднем компании с низкими ценами акций должны подрасти в будущем, а компании с высокими ценами должны упасть. Возврат к среднему также предсказывает, что за повышением должно последовать снижение, и наоборот. Можем ли мы использовать эту информацию, покупая акции, которые только что упали, и продавая акции, которые только что выросли?
Ответ на этот вопрос почти наверняка – нет. Предположим, что произошло возвращение к среднему значению цен на акции. Умные инвесторы поймут это, будут следовать описанной выше стратегии и заработают много денег. Но если достаточное количество инвесторов будет следовать этой стратегии, возврат к среднему значению исчезнет, потому что акции с низкими ценами будут расти, а цены акций с высокими ценами будут снижаться в ответ на решения рынка о покупке и продаже. Гипотеза эффективного рынка гласит, что, поскольку большое количество трейдеров ищет такого рода возможности, мы не сможем предсказать изменения цен на акции, и, следовательно, нам не следует ожидать возврата к среднему значению.
Возврат к среднему значению довольно распространен в деловом мире. Мы видим это в отношении корпоративных доходов и прибылей, несмотря на желание стартапов и венчурных капиталистов прогнозировать будущие доходы, делая линейные, а иногда и экспоненциальные прогнозы на основе прошлых доходов. Так почему же мы не видим возврата к среднему значению цен на акции? Основная причина в том, что цены на акции отражают представления о будущем, а доходы – нет. Цена акций определяется убеждениями инвесторов в долгосрочной стоимости компании. И если бы происходило возвращение к среднему значению, это означало бы, что инвесторы совершают систематические ошибки при формировании своих убеждений. Если бы существовали акции, цена которых должна в будущем гарантированно вырасти, все инвесторы кинулись бы их скупать, моментально подняв цену акций и аннулируя наши ожидания.
Когда дело касается убеждений, понятие возврата к среднему значению неприменимо.
Глава 9. Почему корреляция и причинно-следственная связь не одно и то же
Начнем с примера, в котором принимаются важные решения о том, как использовать ресурсы, и где мы можем с некоторой уверенностью отделить корреляцию от причинно-следственной связи. В США есть чартерные школы, которые работают за государственный счет, но независимо от системы государственных школ. Во многих районах количество детей, подающих заявки на поступление в чартерные школы, превышает возможности зачисления. По закону, когда число желающих учиться в чартерной школе превышает количество учащихся, она должна принимать учеников посредством лотереи.
В качестве примера рассмотрим школу Пройсса (Preuss School) – чартерную школу, созданную Калифорнийским университетом в Сан-Диего. Дети из школы Пройсса учатся намного лучше, чем их сверстники в государственных школах Сан-Диего:
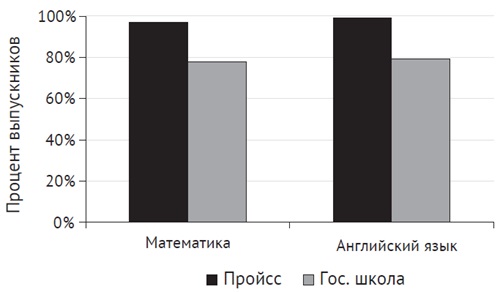
Рис. 4. Результаты стандартизированных тестов в школе Пройсса и городских школах Сан-Диего
Но талант детей и участие родителей сами по себе являются весьма важными факторами, определяющими успеваемость учащихся. Предположим, что контингент учащихся, участвующих в лотереях чартерных школ (и, следовательно, попадающих в эти школы), в среднем более талантлив и происходит из семей, более заинтересованных в образовании, чем население в целом. Когда учеников, выигравших в лотерею, сравнивают с учениками, проигравшими в лотерею, корреляция исчезает – разницы в успеваемости практически нет.
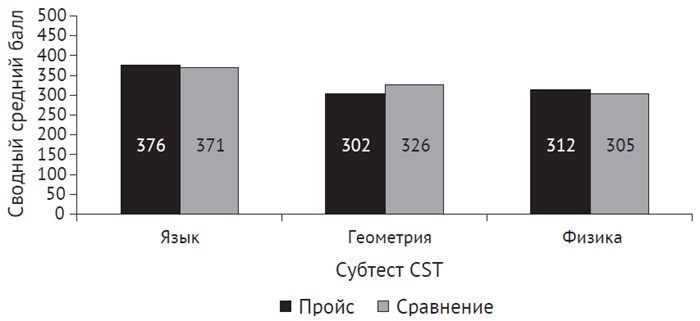
Рис. 5. Сравнение результатов стандартизированных тестов детей, выигравших и не выигравших вступительную лотерею в школу Пройсса
Когда мы сравниваем яблоки с яблоками, оказывается, что высокоэффективные чартерные школы практически не влияют на успеваемость учащихся. Большинство очевидных успехов этих школ связано с тем фактом, что дети, участвующие в лотереях чартерных школ, уже отличаются от среднестатистического ученика в плане обучения. В любом случае их успехи в учебе будут выше среднего. Такое отделение корреляции от причинно-следственной связи может изменить ваши взгляды на то, как нам следует тратить ресурсы на образование.
Чтобы правильно интерпретировать корреляции, нам необходимо отчетливо понимать, когда возникают систематические базовые различия, поскольку именно они приводят к смещению. Есть два основных источника таких различий: искажающие факторы и обратная причинно-следственная связь. Изучение победителей и проигравших в лотерею помогло опровергнуть причинно-следственную связь, поскольку разорвало связь между талантом (искажающий фактор) и посещением школы Пройсса (воздействие). Обратная причинность существует, если результат каким-то образом меняет воздействие.
Глава 15. Как наделить статистику смыслом
Существует два способа указать размер эффекта: изменение результата, который он вызывает, в процентах или в процентных пунктах. Изменение в процентных пунктах – это разница между двумя процентными значениями. Изменение в процентах – это разница между двумя процентными значениями, деленная на первоначальное значение. Например, переход от 20% к 22% означает увеличение на 2 процентных пункта (22% минус 20%), или рост на 10% (2/20). Вот пример.
The Wall Street Journal сообщила о медицинском эксперименте, который показал, что новый препарат снижает «риск смерти от сердечных заболеваний, сердечных приступов и других серьезных проблем с сердцем на 44%». Звучит солидно. На самом деле базовый риск сердечного приступа составляет около 2,8%. Снижение частоты сердечных приступов на 44% означает переход к 1,6 %. В статье используются статистические данные, отвечающие на вопрос, вызывает ли препарат заметное снижение количества сердечно-сосудистых заболеваний? Ответ положительный. Но заголовок создает впечатление, будто данные отвечают на гораздо более важный вопрос, спасет ли препарат много жизней? В статье нет ответа. Преобразовав статистический показатель (процентное снижение) в суть (количество предотвращенных сердечных приступов на 100 пролеченных человек), мы можем легко обнаружить разницу и ответить на вопросы, наиболее важные для принятия решений.
Правило Байеса и количественный анализ
Правило Байеса позволяет оценить, насколько мы можем быть уверены в истинности некоторой научной гипотезы в свете доказательств, представленных в научном исследовании. Ранее мы узнали, что p-значение говорит, насколько вероятно, что данный результат получен случайно. Но если вдуматься, то станет ясно, что это не ответ на правильный вопрос. Аналитик рассчитал вероятность того, что он нашел бы связь в своих данных, даже если бы в мире не было реальной связи, т.е. Рг(результат | связь отсутствует). На самом деле нужно знать, насколько вероятно отсутствие реальной связи при имеющемся результате, то т. е. Рг(связь отсутствует | результат). Вероятность существования реальной связи при условии данного результата равна 1 – Рг(связь отсутствует | результат).
Предположим, мы получили p < 0,05. Какова вероятность того, что предполагаемая взаимосвязь отражает реальное явление, а не появляется в данных из-за шума? По правилу Байеса:
![]()
Знаменатель можно разбить на два слагаемых:
- взаимосвязь реальна и тест правильно ее определил – Рr(связь существует) * Рr(результат | связь существует);
- взаимосвязи нет, но тест ошибочно идентифицирует ее как реальную из-за шума – Рr(связь отсутствует) * Рr(результат | связь отсутствует).
Можно переписать (6) в виде:
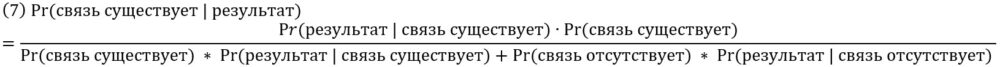
Мы знаем Рr(результат | связь отсутствует). Это – уровень значимости, используемый при проверке гипотезы = 0,05. Остальные числа найти сложнее. Величина Рr(связь существует) – наше априорное убеждение в том, что настоящая связь существует, до того, как мы увидели какие-либо новые свидетельства. Величина Рr(результат | связь существует) – вероятность того, что мы найдем взаимосвязь в ваших данных при условии, что она действительно существует. И это статистическая мощностью теста (подробнее см. Статистическая мощность эксперимента в Excel). Статистическая мощность представляет собой ответ на следующий вопрос: какова вероятность того, что мы обнаружим статистически значимый результат в данных, при условии, что взаимосвязь реальна?
Перепишем правило Байеса с учетом более предметной интерпретации величин:

Предположим, у нас есть догадка о некой причинно-следственной связи. Пока это лишь слабое предположение. Мы считаем, что вероятность существования этого эффекта составляет 5% (наше априорное убеждение). Затем проводим рандомизированный эксперимент. Мы хотим быть уверены в ответе, поэтому обеспечиваем большой размер выборки, такой, что статистическая мощность теста будет равна 80%. Мы используем порог статистической значимости 5%. Каким будет апостериорное убеждение относительно вероятности того, что эффект реален, при условии, что наблюдается статистически значимый результат?
![]()
Что случилось? Даже при условии получения результата, статистически значимого на уровне 95%, вероятность того, что эффект, который мы наблюдаем, существует на самом деле, составляет всего 46%! Если наши априорные убеждения низки (5%), наши апостериорные убеждения, вероятно, также будут низкими.
Эти рассуждения помогают нам лучше понять кризис репликации во многих научных дисциплинах. Каково априорное убеждение относительно проверяемых гипотез? Вероятно, довольно низкое. Как следствие, апостериорное убеждение в том, что эффект реален, даже при наличии статистически значимых доказательств, не так уж велико. Следующий рисунок дает наглядное представление об этом. Вертикальная ось представляет собой апостериорную вероятность того, что наблюдаемая связь реальна. Горизонтальная ось – это априорная вероятность того, что она реальна. Кривая отображает правильное апостериорное убеждение как функцию вашего априорного убеждения при условии, что исследование со статистической мощностью 0,8 и порогом значимости 0,05 дало статистически значимые доказательства существования взаимосвязи.
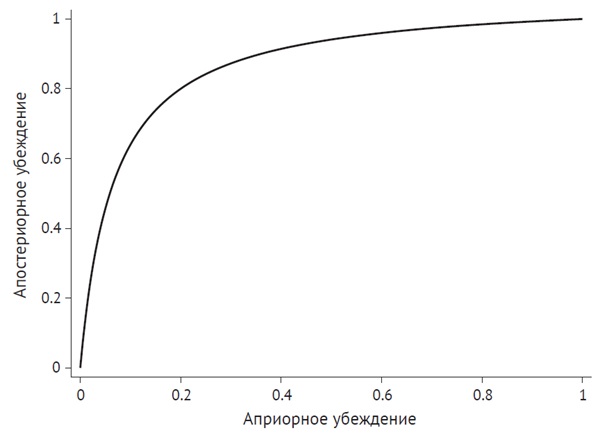
Рис. 6. Апостериорное убеждение в том, что эффект реален при наличии статистически значимых доказательств, как функция априорного убеждения
Наши априорные убеждения чрезвычайно важны для формирования апостериорных убеждений. Например, если у вас чрезвычайно низкое априорное убеждение относительно существования экстрасенсорного восприятия, то, возможно, даже не имеет смысла его изучать, потому что результаты исследования практически не окажут влияния на ваши убеждения.
На рис. 7 показано, как изменение убеждений в ответ на новые данные соотносится с априорным убеждением. Здесь изображено ваше апостериорное убеждение в том, что реальная взаимосвязь существует, минус ваше априорное убеждение в том, что взаимосвязь существует, для различных значений априорного убеждения при условии, что вы наблюдали статистически значимые доказательства в пользу этой взаимосвязи. Как видите, если ваше априорное убеждение уже очень близко к 0 или 1, изменить его очень сложно. Эффект новых данных является наибольшим для умеренно неожиданных результатов (т.е. результатов, для которых ваше априорное убеждение было около 0,2).
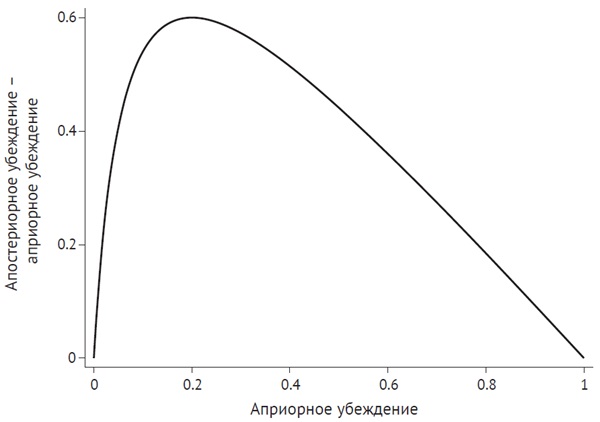
Рис. 7. Разница между апостериорными и априорными убеждениями в ответ на новые доказательства в зависимости от априорных убеждений
Два человека могут (и должны) совершенно по-разному реагировать на одну и ту же информацию, если у них разные априорные убеждения. Некоторые люди могут увидеть какое-то свидетельство об экстрасенсорном восприятии, последствиях глобального потепления или вмешательстве России в американские выборы и резко изменить свои убеждения, в то время как другие могут увидеть те же доказательства и вообще почти не изменить свои убеждения. Когда мы сталкиваемся с этим в повседневной жизни, то часто приходим к выводу, что люди, которые реагировали иначе, чем мы, неразумны или иррациональны. Но правило Байеса говорит нам, что совершенно естественно, когда разные люди по-разному реагируют на одну и ту же информацию, если вначале у них были разные априорные убеждения.
Выводы из наших рассуждений могут вызвать у вас дискомфорт. Разве мы, аналитики данных, не должны позволить данным говорить непредвзято, не навязывая собственных предубеждений? И откуда берутся эти априорные убеждения, если не из данных? Это трудные вопросы. Но обойти их невозможно. Если вы хотите что-то сказать о вероятности существования подлинной причинно-следственной связи при наличии каких-либо доказательств, вам необходимо иметь априорные убеждения о вероятности этой связи. Вы не можете просто игнорировать свои априорные убеждения.
Глава 16. Измерение показателей вашей миссии
Есть еще один интересный вопрос. Иногда в мире существуют отношения между событиями или объектами, которые вы могли бы использовать для достижения своей цели. Но как только вы попытаетесь это сделать, стратегическая адаптация заставит эти отношения исчезнуть или измениться, и они перестанут быть такими полезными. Чтобы понять, как это происходит, рассмотрим исторический пример.
В 1696 г. английскому королю Вильгельму III понадобились деньги. Вплоть до 1660-х гг. Британия производила монеты из чеканного серебра. У этих монет была серьезная проблема: люди соскабливали или срезали ценное серебро с краев монет. В результате стоимость монет в серебре оказалась меньше их номинала. Эта широко распространенная практика обрезки монет угрожала подорвать доверие к английской валюте.
Чтобы решить эту проблему, Корона затеяла большую перечеканку монет в 1696 г., предложив выкупить обрезанные монеты в обмен на новые, обработанные на станке монеты, которые нельзя было обрезать . Но выкуп обрезанных монет за настоящие монеты обходился дорого. По сути, Корона должна была компенсировать разницу между номинальной стоимостью монеты и стоимостью серебра. Итак, Короне необходимо было увеличить доходы. Но как это сделать?
Корона хотела облагать богатых более высоким налогом, чем бедных. Одним из естественных способов добиться этого является введение подоходного налога. Но англичане были против подоходного налога, поскольку оценка дохода подразумевала вторжение в личную жизнь. Поэтому Короне нужно было найти способ налогообложения богатства, более приемлемый с политической точки зрения. Решением стал налог на окна.
Налог на окна имел то преимущество, что его можно было взимать по результатам внешнего осмотра дома, тем самым исключая любое вторжение в частную жизнь. В самой ранней версии налога Корона установила базовую плату в размере двух шиллингов за все дома. Кроме того, дома, в которых было от десяти до двадцати окон, платили дополнительно от четырех до шести шиллингов, а дома, в которых было более двадцати окон, платили дополнительно от восьми до десяти шиллингов. Окна в рабочих помещениях не учитывались.
Аргументом в пользу налога на окна была очевидная корреляция между окнами и богатством. В среднем люди, в чьих домах было больше окон, были богаче. Облагая налогом окна, Корона могла увеличить доходы таким образом, чтобы большая часть бремени ложилась на богатых и меньшая на бедных, что и было ее миссией.
Но на этом история не заканчивается. Англичане, как и многие другие народы, не любят платить налоги. И поэтому они стратегически адаптировались. Очень быстро многие окна были заколочены или заложены кирпичом, чтобы уменьшить причитающиеся налоги. Со временем архитектура изменилась. В больших домах стало меньше окон и больше комнат, которые можно было представить как рабочие помещения. Таким образом, с течением времени как доходы Короны, так и прогрессивность налога на окна снизились.
В данном случае миссией Короны было постепенное увеличение доходов. Для этого необходимо было выявить и обложить налогом более богатых людей, не вторгаясь в их частную жизнь. Авторы идеи заметили корреляцию между окнами и богатством, которая, казалось, была именно тем, что нужно для достижения цели. Но использование этой корреляции заставило домовладельцев стратегически адаптировать свое поведение так, чтобы корреляция больше не сохранялась (или, по крайней мере, сохранялась гораздо менее сильно), что подрывало миссию. Следовательно, обсуждая изменения в поведении или политике в ответ на какие-то наблюдения, всегда нужно задаваться вопросом, сохранится ли взаимосвязь, выявленная этими наблюдениями, после того как вы измените свое поведение или политику.
Закон на окна действовал до середины XIX века, но традиции в Англии столь сильны, что даже сейчас новые дома строят с окнами, заложенными кирпичами.
Глава 17. О пределах возможностей количественной оценки
Какими бы важными ни были количественные данные, не существует такой вещи, как решение, основанное исключительно на данных. Это верно как минимум по двум причинам. Во-первых, для многих важных решений достоверные данные ограничены или даже отсутствуют. Но решения все равно приходится принимать. На самом деле даже решение ничего не делать – это тоже решение. Поэтому важно четко понимать, что нам делать, когда мы сталкиваемся с отсутствием данных.
Во-вторых, правильное решение никогда не может быть определено только на основе количественного анализа. Анализ призван стать инструментом, используемым для достижения наших целей и ценностей. Но иногда кажется, что хвост виляет собакой – мы подгоняем свои ценности под требования количественной оценки.
Не все можно легко измерить или дать количественную оценку. Ограниченное «пятно света» в мире, управляемом данными, сужает нашу точку зрения, заставляя сосредоточиться только на тех вещах, где доступны количественные свидетельства.
Во-первых, мы можем просто игнорировать критически важные проблемы, потому что не понимаем, как принять решение, основанное на фактических данных. Во-вторых, требование доказательств может создать своего рода предвзятость статус-кво, т.е. стремление ничего не менять, если количественных данных недостаточно.
Количественные данные должны помогать нам принимать более правильные решения, которые способствуют достижению наших целей и ценностей. Но если мы не будем осторожны, ситуация может измениться на противоположную: наши цели и ценности будут определяться доступностью количественных данных.
Во-первых, количественные инструменты иногда могут незаметно для нас внести в процесс принятия решений ценности, с которыми мы не согласны. Во-вторых, стремление соответствовать количественной оценке может подтолкнуть нас к принятию ценностей, которые в противном случае мы могли бы отвергнуть.
Один из рисков количественной оценки, особенно в эпоху, когда машинное обучение и алгоритмическое принятие решений становятся все более распространенными, заключается в том, что нежелательные ценности могут проникнуть в решения незаметно для нас. Алгоритмы машинного обучения – это в большей или меньшей степени просто причудливые способы использования корреляций для прогнозирования. Алгоритм, который не учитывает расовую или гендерную принадлежность, т.е. не имеет доступа к данным о расе или поле, тем не менее может в конечном итоге делать прогнозы, которые по-разному относятся к людям с разной расовой или гендерной идентичностью. Это может произойти, например, если алгоритм имеет доступ к данным о переменных, которые коррелируют с расой.
Что отличает вульгарный утилитаризм от всех других нормативных рамок, так это то, что он легко поддается количественному анализу. Трудно понять, как количественно измерить ценность прав и обязанностей или как взвесить соображения справедливости. Гораздо проще дать количественную оценку материальных затрат и выгод, а затем просто складывать и вычитать, чтобы выяснить, насколько хороша та или иная политика.
Действительно, с вульгарным утилитаризмом настолько удобно работать, что он стал частью стандартных предположений, лежащих в основе многих количественных анализов, особенно в дискуссиях о государственной политике. Стремление максимизировать чистое благосостояние – игнорирование вопросов прав, обязанностей, ответственности, справедливости, достоинства и т.д. – настолько укоренилось в нашем поведении и мышлении, что мы даже не замечаем этого. Мы просто считаем само собой разумеющимся, что хорошая политика – это та, которая максимизирует выгоды за вычетом затрат. Мы преследуем не те цели и ценности, которые хотелось бы, а те, которые поддаются количественной оценке. Мы утилитаристы не потому, что таковы наши убеждения. Нас делает утилитаристами стремление работать только с измеримыми величинами.
Оцените по достоинству, как усердно вы работали над этой книгой и как далеко мы продвинулись вместе. Теперь вы являетесь членом небольшой, но растущей группы людей, которые могут ясно и непредвзято думать о проблеме выбора зависимой переменной, о разнице между статистической и существенной значимостью, возврате к среднему значению, предвзятости публикации, источниках «космического привыкания», взаимосвязи между корреляцией и причинностью, планах исследования и многом другом. Это фундаментальные навыки, которые будут служить вам всегда, даже если вы больше никогда не построите ни одну регрессию. Ведь мы живем в такое время, когда критическое мышление в отношении данных абсолютно необходимо всем, кто хочет понять мир и сделать его лучше.
[1] Выборочное распределение в смысле распределения средних значений выборок.