Каковы шансы поймать нечестную монету?

Возможно, вы слышали про парадокс дней рождения. Ответьте на вопрос: сколько человек должно быть в группе, чтобы вероятность совпадения дней рождения (число и месяц) хотя бы у двух людей превысила 50%? Прежде чем читать далее, дайте быстрый приблизительный ответ.

Скачать заметку в формате Word или pdf, примеры в формате Excel

Если принять во внимание, что вероятность совпадения дней рождения в группе из двух человек, равна 1/365=0,27% (без учета високосных лет), то можно решить, что потребуется группа из более чем 180 человек, чтобы вероятность совпадения превысила 50%.

На самом деле в группе из более чем двух человек число пар быстро возрастает, поэтому вероятность совпадения можно искать по формуле комбинаторики, например, такой:

где р(n) – вероятность совпадения дней рождения хотя бы у двух человек в группе из n человек.

Построим график функции р(n) в Excel.

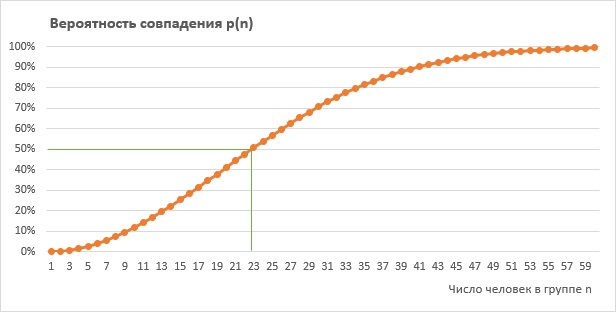
Рис. 1. График вероятности совпадения дней рождения хотя бы у двух человек из группы размером n

Видно, что вероятность 50% достигается в группе всего из 23 человек. С точки зрения математики никакого парадокса нет. Парадокс возникает между нашей интуицией и расчетом.

Аналогичный феномен можно увидеть и в восприятии нами того, легко ли выявить нечестную монету. Допустим, вы выполнили 10 бросков и орел появился 7 раза. На ваш взгляд, есть ли основания считать монету нечестной?

Статистический вывод

Такого рода вопросы рассматриваются в рамках статистического вывода. В статистическом выводе на основе случайной выборки делаются предположения относительно генеральной совокупности. Наши 10 бросков – это выборка. Статистический вывод позволяет оценить, с какой вероятностью выборка происходит из генеральной совокупности [бесконечно большого числа бросков] честной монеты или генеральной совокупности нечестной монеты.

Для начала сравним, как будут распределены вероятности для выборок (при n = 10), проистекающих из двух генеральных совокупностей – «честной» и «нечестной». Понятно, что распределение для честной монеты одно, а для нечестных – множество. Только для примера предположим, что нечестная монета с вероятностью 70% падает орлом, и 30% – решкой.

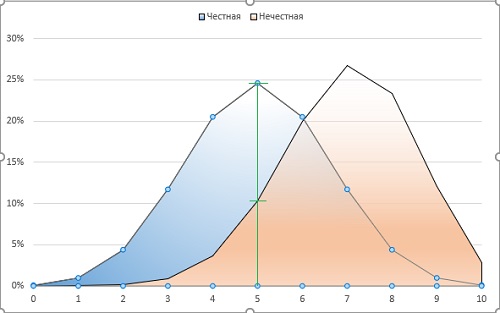
Рис. 2. Вероятности выпадения орла в десяти бросках

Еще раз, что показывает график? С какой вероятностью в серии из 10 бросков выпадет 0, 1, 2, …, 10 орлов, если монета честная (синяя кривая) или нечестная (рыжая кривая). Например, выборка с 5 орлами в случае честной монеты появится с вероятность 24,6%, а в случае нечестной монеты – 10,3%.

Но у нас нет рыжего графика. Мы лишь знаем априорное (теоретическое) распределение для честной монеты, и провели эксперимент – бросили монету 10 раз, получив в серии 7 орлов. Так у нас в руках честная монета или нет?

Проверка гипотез

Статистический вывод основан на проверке гипотез. Гипотеза – некое утверждение об интересующем нас параметре генеральной совокупности. В нашем примере гипотеза заключается в том, что выборка из 10 бросков с 7 орлами проистекает из генеральной совокупности с выпадением орлов c математическим ожиданием μ = 5. Гипотеза о том, что параметр генеральной совокупности равен ожидаемому, называется нулевой и обозначается Н₀:μ = 5.

Обратите внимание: при том, что нам доступна информация об одной выборке, нулевая гипотеза относится к параметру всей генеральной совокупности. В этом суть процедуры статистического вывода! Еще раз:

в статистическом выводе на основе случайной выборки делаются предположения относительно генеральной совокупности

Статистический вывод может показать, что нулевая гипотеза неверна. Поэтому также необходимо сформулировать альтернативную гипотезу. Она будет считаться истинной, если нулевая гипотеза будет отвергнута. Альтернативная гипотеза Н₁ противоположна нулевой гипотезе Н₁:μ ≠ 5.

Формулировка альтернативной гипотеза не столь тривиальна, как кажется. Например, по каким-то причинам, мы можем знать, что нечестная монета увеличивает вероятность орлов, но не уменьшает. Тогда альтернативная гипотеза будет односторонней Н₁:μ > 5.

В связи с проверкой гипотез важно понимать следующее:

• Нулевая гипотеза Н₀ отражает статус-кво, или отсутствие особенностей. Например, если мы говорим об эффективности рекламы, то нулевая гипотеза заключается в том, что реклама не увеличивает продажи)) Нулевая гипотеза не требует доказательств.
• Альтернативная гипотеза Н₁ отрицает нулевую и является нашим предположением, которое требуется доказать.
• Если нулевая гипотеза отвергается, альтернативная гипотеза считается истинной.
• Если нулевая гипотеза не отвергается, альтернативная считается недоказанной. Её недоказанность не означает, что нулевая гипотеза верна.

Параметр генеральной совокупности и статистика выборки

В нашем примере нулевая гипотеза означает, что в среднем в выборке должно содержаться 5 орлов. В этом случае параметр генеральной совокупности (в нашем случае это математическое ожидание) μ равен теоретическому (для случая честной монеты). То количество орлов, которое присутствует в нашей одиночной выборке х̅, называется статистикой. Статистика позволяет дать оценку соответствующего параметра генеральной совокупности, из которой извлечена выборка. Даже если нулевая гипотеза истинна, из-за изменчивости выборочное среднее не обязано в точности совпадать со средним значением генеральной совокупности. Однако в этом случае можно ожидать, что выборочное среднее будет мало отличаться от математического ожидания генеральной совокупности.

С другой стороны, если между выборочной статистикой и параметром генеральной совокупности наблюдаются значительные различия, возникает желание отклонить нулевую гипотезу. Например, если при 10 бросках орлов не было, можно заподозрить, что математическое ожидание генеральной совокупности не равно номинальному (т.е. μ ≠ 5). В любом случае статистический вывод основывается на предположении, что случайные выборки являются репрезентативными и правильно представляют свойства генеральной совокупности, из которой они извлечены.

К сожалению, процесс принятия решения на практике не так прост. Он существенно зависит от субъективного восприятия понятий «большое отклонение» и «небольшое отклонение». Проверка гипотез позволяет формализовать эти понятия… но не добавляет объективности.

Процедура статистического вывода включает:

• вычисление выборочной статистики (в нашем примере число орлов в 10 бросках),
• выбор статистики, положенной в основу критерия размежевания.

Статистика критерия размежевания

Бросание монеты подчиняется биномиальному распределению. Его математическое ожидание равно произведению объема выборки n на вероятность успеха р. Для честной монеты в серии из 10 бросков среднее:

а стандартное отклонение:

Дискретное биномиальное распределение для целей размежевания можно аппроксимировать нормальным распределением.[1]

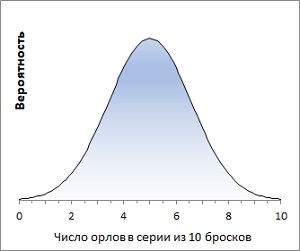
Рис. 3. Нормальное распределение для μ = 5 и σ = 1,58

Критерий размежевания нулевой и альтернативной гипотез

Представленная на рис. 3 статистика для целей размежевания разделяется на две части. По краям симметрично располагаются области отклонения нулевой гипотезы, также называемые критическими областями. В центре – область принятия нулевой гипотезы.

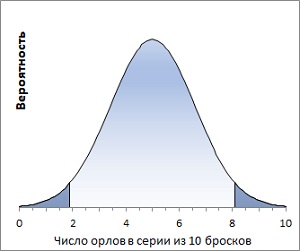
Рис. 4. Области принятия и отклонения нулевой гипотезы

Если альтернативная гипотеза односторонняя, вся область отклонения нулевой гипотезы будет лежать с одного края.

Когда статистика выборки попадает в область принятия гипотезы, нулевую гипотезу отклонить нельзя. Если статистика выборки попадает в критическую область, нулевая гипотеза отклоняется. В этом случае мы говорим, что монета нечестная.

При проверке гипотез сначала следует определить критическое значение. Оно отделяет область принятия нулевой гипотезы от области отклонения нулевой гипотезы. Критическое значение определяется через вероятность области отклонения нулевой гипотезы. Размер критической области непосредственно связан с величиной риска, возникающего, когда параметр генеральной совокупности оценивается по выборочным данным.

Риски, возникающие при проверке гипотез

При оценке параметра генеральной совокупности по выборочным значениям существует риск прийти к неверным выводам. При проверке гипотез возможны два типа ошибок: 1- и 2-го рода. В нашем сценарии ошибка 1-го рода возникает, когда мы считаем, что монета нечестная, в то время как на самом деле она честная. С другой стороны, если мы держимся нулевой гипотезы и считаем, что монета честная, в то время как на самом деле она нечестная, возникает ошибка 2-го рода.

Еще раз, ошибка 1-го рода возникает, когда отклоняется истинная нулевая гипотеза Н₀. Вероятность ошибки 1-го рода обозначается буквой α. Альфа – вероятность, или площадь хвоста кривой распределения, а не значение по оси Х. На рис. 4 темно синие области по краям в совокупности составляют 5% общей площади под кривой. Таким образом мы постулировали величину ошибки первого рода α = 0,05. В Excel левое критическое значение можно найти по формуле: =НОРМ.ОБР(α/2;μ;σ). Для α = 0,05 на каждую критическую область приходится по 0,025 вероятности. Как мы рассчитали в формулах (2) и (3) μ = 5, σ = 1,58. Таким образом левая граница: НОРМ.ОБР(0,025;5;1,58) = 1,9. Правая граница НОРМ.ОБР(1-0,025;5;1,58) = 8,1.

Ошибку 1-го рода также называют уровнем значимости. Поскольку уровень значимости задается, он находится под полным контролем лица, выполняющего проверку. Часто выбирают уровни значимости α равные 0,01, 0,05 или 0,1. Почему же не минимизировать ошибку первого рода, и не дать альфе минимальное значение!? Потому, что возрастет ошибка второго рода: мы гораздо чаще [чем нужно] будем держаться нулевой гипотезы. На эту тему позвольте поучительный анекдот.

Муж заподозрил жену в неверности и нанял частного детектива, чтобы следить за ней. Через некоторое время детектив докладывает о проделанной работе:

– Они поговорили, выпили и начали раздеваться.

– Ну, а дальше? Что было дальше? – в нетерпении спрашивает муж.

– А дальше они погасили свет, и я ничего не смог увидеть.

– Ах, опять эта проклятая неизвестность!

Здесь нулевая гипотеза – жена сохраняет верность. А критическое значение для мужа настолько далеко отстоит от среднего, что он придерживается нулевой гипотезы слишком рьяно… упуская возможность принять альтернативную гипотезу.

Ошибка 2-го рода возникает, когда не отклоняется ложная нулевая гипотеза Н₀. Вероятность ошибки 2-го рода обозначается буквой β. В отличие от ошибки 1-го рода, которая задается экспериментатором, ошибку 2-го рода можно оценить лишь качественно.

Ошибка 2-го рода и статистическая мощность

Вероятность ошибки 2-го рода можно визуально представить как площадь под кривой распределения альтернативной гипотезы, лежащая в пределах области принятия нулевой гипотезы:

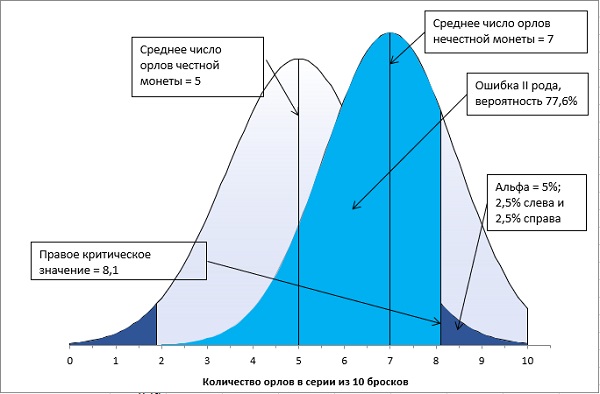
Рис. 5. Вероятность ошибки 2-го рода

Ошибка 2-го рода – голубая область лежащая под кривой распределения альтернативной гипотезы (нечестной монеты) от нуля до критического значения 8,1.

Вероятность события, дополняющего ошибку 2-го рода до единицы называют статистической мощностью. Статистическая мощность по определению равна 1 – β.

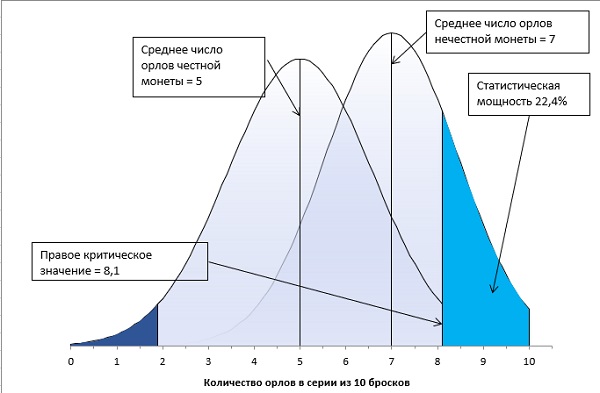
Рис. 6. Статистическая мощность для выборок с n = 10

В нашем сценарии статистическая мощность равна вероятности прийти к выводу, что монета нечестная, когда она действительно нечестная. Можно также сказать, что статистическая мощность равна вероятности отклонить ложную нулевую гипотезу Н₀. Видно, что наш эксперимент обладает небольшой статистической мощностью. Вероятность отклонения ложной нулевой гипотезы составляет всего 22,4%.

На самом деле, всё еще интереснее! Если распределение честной монеты полностью детерминировано, то гипотетическое распределение нечестной монеты нам не известно. Всё, что у нас есть – одиночная выборка. С какой вероятностью нечестная монета выпадает орлом – 0,7, 0,6, 0,8, … – мы не знаем. Вспомните, что альтернативную гипотезу мы сформулировали в самом общем виде – Н₁:μ ≠ 5. Если бы в качестве альтернативной гипотезы выступала Н₁:μ = 7, приведенные выше расчеты имели бы право на существование.

Несмотря на то, что расчет статистической мощность в общем случае выполнить нельзя, теория подсказывает, какие факторы позволяют увеличить мощность:

1. Уровень α. Посмотрите на рис. 6. Более высокая α смещает критическое значение от хвоста к центру, увеличивая голубую область.
2. Тип теста. Переход от двунаправленной альтернативной гипотезы к однонаправленной переносит всю вероятность в один хвост, что также смещает критическое значение от хвоста к центру, и увеличивает мощность.
3. Разница между математическим ожиданием генеральной совокупности μ (для честной монеты) и средними значением выборки х̅. Если бы выпало 8 орлов, правый колокол сместился еще больше вправо, что увеличило голубую область на рис. 6.
4. Первые три фактора часто неподвластны нам в эксперименте. Поэтому четвертый фактор может стать основным. Увеличьте размер выборки n. Это приведет к уменьшению стандартного отклонения. Колоколообразные кривые станут более узкими. Отличие среднего по выборке станет более отчетливым.

Посмотрите, что произойдет, если мы увеличим n до 100 (сравните с рис. 2):

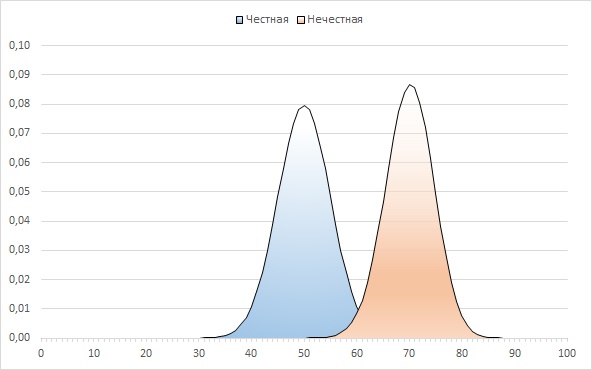
Рис. 7. Плотность вероятности для n = 100

Для n = 100, статистическая мощность при тех же условиях (Н₁:μ ≠ 5, двунаправленный тест, α = 5%) дает великолепные 98,7%. Т.е., сделав 100 бросков, и получив 70 орлов, с вероятностью 98,7% нам следует отклонить нулевую гипотезу Н₀:μ = 5.

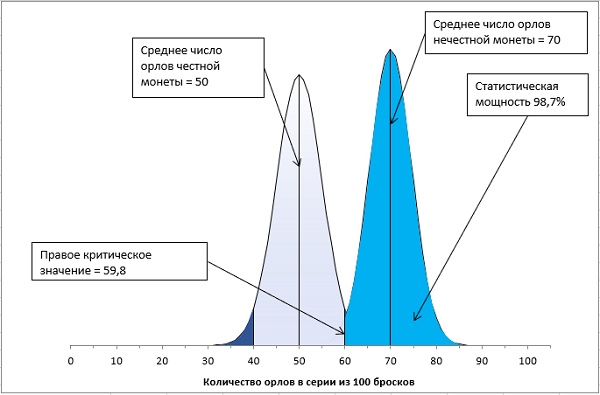
Рис. 8. Статистическая мощность для выборок с n = 100

Суть статистического вывода

Соберем все шаги вместе. Мы начали с выборки n = 10, в которой орел появился 7 раз. Вопрос, является ли монеты честной, привел нас к процедуре статистического вывода. Мы сформулировали нулевую и альтернативную гипотезы: Н₀:μ = 5, Н₁:μ ≠ 5. Далее мы увидели, что критерий признания/отклонения нулевой гипотезы является субъективным. Чем чаще отклонение от среднего мы не будем считать критичным, тем дольше мы будем держаться за нулевую гипотезу… И тем реже будем признавать истинность альтернативной гипотезы. Мы ввели понятие статистической мощности – вероятности признания альтернативной гипотезы, когда она верна. И показали, что повысить статистическую мощность можно путем увеличения размера экспериментальной выборки.

В начале заметки я спрашивал:

Допустим, вы выполнили 10 бросков и орел появился 7 раза. На ваш взгляд, есть ли основания считать монету нечестной?

Теперь вы можете сказать, что появление 7 орлов в серии из 10 бросков не позволяет признать монету нечестной. В то же время появление 70 орлов в серии из 100 бросков почти наверняка свидетельствует о нечестности монеты.

[1] На самом деле в целях размежевания используют более сложные статистики. Но для первого знакомства со статистическим выводом, я решил не усложнять.