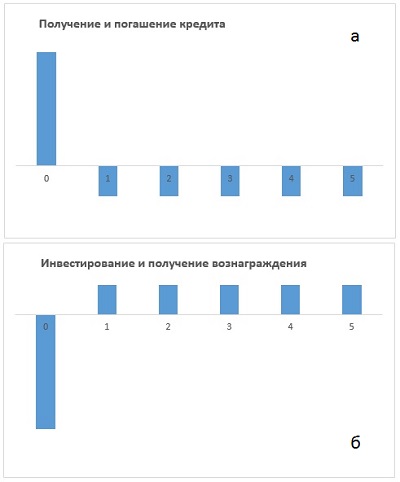
Около 20 лет назад я работал в издательстве. Собственник видел, что основная деятельность приносит всё меньше доходов, и я рассказал о возможности инвестировать средства сегодня, и получать выплаты в течение всей жизни. На похожем принципе основан нобелевский фонд. Согласно завещанию Альфреда Нобеля, на премии можно было направлять только проценты, полученные на стоимость активов фонда. Активы фонда с течением времени не уменьшаются, а расходуется только дополнительный капитал. В общем случае аннуитет — график платежей (в счет погашения кредита или получения вознаграждения на инвестиции) равными суммами через равные промежутки времени (рис. 1). Формулы для этих двух вариантов идентичны, и отличаются только знаком.
Рис. 1. Аннуитетные платежи: а) кредитование; б) инвестирование. По оси абсцисс – периоды времени, по оси ординат – суммы.
Скачать заметку в формате Word или pdf, примеры в формате Excel
Аннуитет – это не вечный финансовый двигатель, а механизм, основанный на том, что одна и та же сумма сегодня и в будущем имеет разную ценность. Аннуитет может быть конечным (количество выплат ограничено) или бесконечным. Последний также называют перпетуитет.
Сумма инвестиций (сегодня) для получения в будущем n выплат определяется формулой:
где, PV – текущая приведенная стоимость инвестиций (present value); Р – сумма разового аннуитетного платежа; n – количество периодов выплаты вознаграждения на инвестиции; r – ставка дисконтирования за период платежа; например, если выплаты раз в год, то ставка годовая; если выплаты раз в месяц, ставка месячная; Аn; r – коэффициент приведения аннуитета. Аn; r показывает, какую сумму достаточно инвестировать в начальный момент времени, чтобы потом регулярно в течении срока, состоящего из n периодов получать платежи единичного размера с учетом регулярного начисления на оставшиеся денежные средства сложных процентов по ставке r за каждый расчетный период (подробнее см. Аннуитетные финансовые функции).
В докомпьютерную эру коэффициент приведения аннуитета находили по специальным таблицам, имеющим дискретный шаг (рис. 2).
Рис. 2. Таблица для определения коэффициента приведения аннуитета; приводится по книге Михаил Лимитовский. Инвестиционные проекты и реальные опционы на развивающихся рынках; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Гораздо проще расчет коэффициента может быть выполнен в Excel для любых n и r с помощью функции =ПС(ставка; кпер; плт; [бс]; [тип])
где ПС – приведенная (к текущему моменту) стоимость займа или инвестиции на основе постоянной процентной ставки;
ставка – процентная ставка за период; например, если получен кредит на автомобиль под 10% годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%);
кпер – число периодов платежей; например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов.
плт – платеж, производимый в каждый период и не меняющийся на протяжении всех выплат; при расчете коэффициента приведения аннуитета плт = –1;
бс – значение будущей стоимости; при расчете коэффициента приведения аннуитета опускается;
тип – число 0 или 1, обозначающее, когда должна производиться выплата; 0 или опущен – в конце периода, 1 – в начале периода; при расчете коэффициента приведения аннуитета опускается.
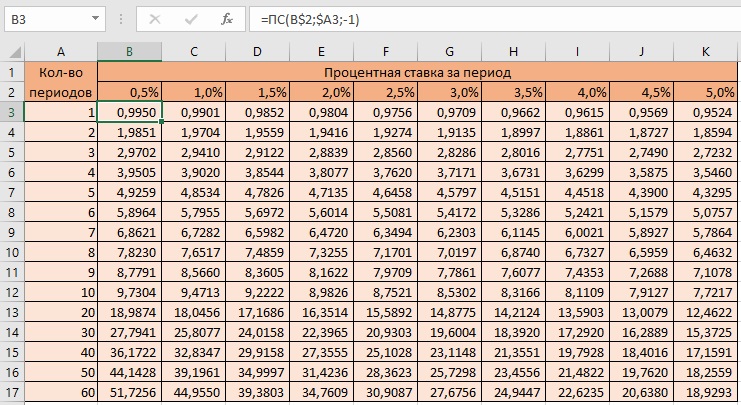
Рассчитаем, фрагмент приведенной выше таблицы в Excel (формулы см. в приложенном Excel-файле на листе «КПА»):
Рис. 3. Расчет коэффициента приведения аннуитета в Excel
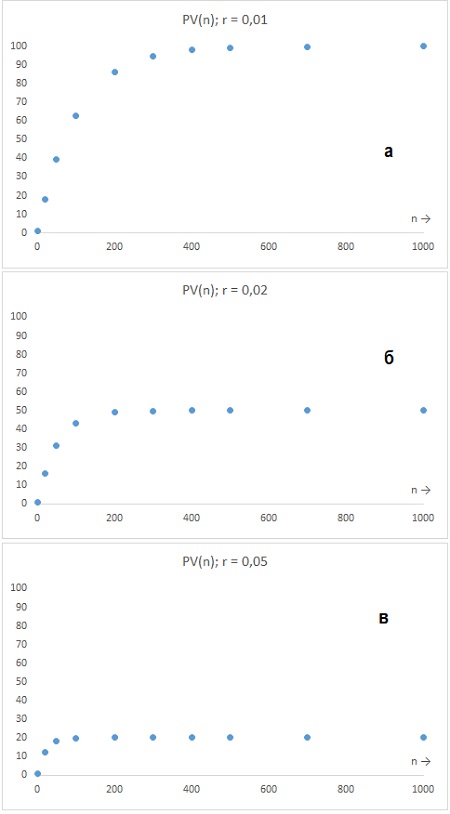
Любопытно отразить на графике зависимость PV(n) для нескольких значений r, например, 1%, 2%, 5%. Видно, что с ростом n, PV стремится к некоторому пределу, который равен 1/r (рис. 4). Этот предел и есть стоимость бессрочного аннуитета (или бессрочной ренты, или перпетуитета). Перпетуитет вычисляется по формуле
Рис. 4. Предел, к которому стремится функция PV(n) равен 1/r: а) r = 1%, PV(n→∞)→100; б) r = 2%, PV(n→∞)→50; в) r = 5%, PV(n→∞)→20