Недавно прочитал Искусство статистики Дэвида Шпигельхалтера. На тему байесовской вероятности очень понравился пример с монетами. Сначала – фрагмент книги, а затем небольшая модель в Excel.
У вас в кармане три монеты: на одной два орла, на другой две решки, третья обычная. Вы наугад вытаскиваете монету, подбрасываете ее, и выпадает орел. Какова вероятность, что на другой стороне монеты тоже орел? Дайте свой ответ, прежде чем читать далее.

Рис. 1. Три монеты
Скачать заметку в формате Word или pdf, примеры в формате Excel
Дерево решений
Многие бы решили, что ответ — 1/2, поскольку монета либо обычная, либо с двумя орлами, и вероятность выбрать одну из них одинакова. Проверим это, нарисовав дерево решений. На рис. 2 показано, чего можно ожидать, если проделать такой эксперимент шесть раз. В среднем каждая монета будет выбрана дважды, и каждая из сторон выпадет по разу. Орел выпадает в трех случаях, причем в двух на второй стороне также будет орел. Поэтому вероятность того, что на второй стороне монеты тоже орел, равна 2/3, а не 1/2. По сути, выпадение орла повышает вероятность выбора монеты с двумя орлами, ведь у такой монеты есть два варианта упасть орлом вверх, а у симметричной — только один.
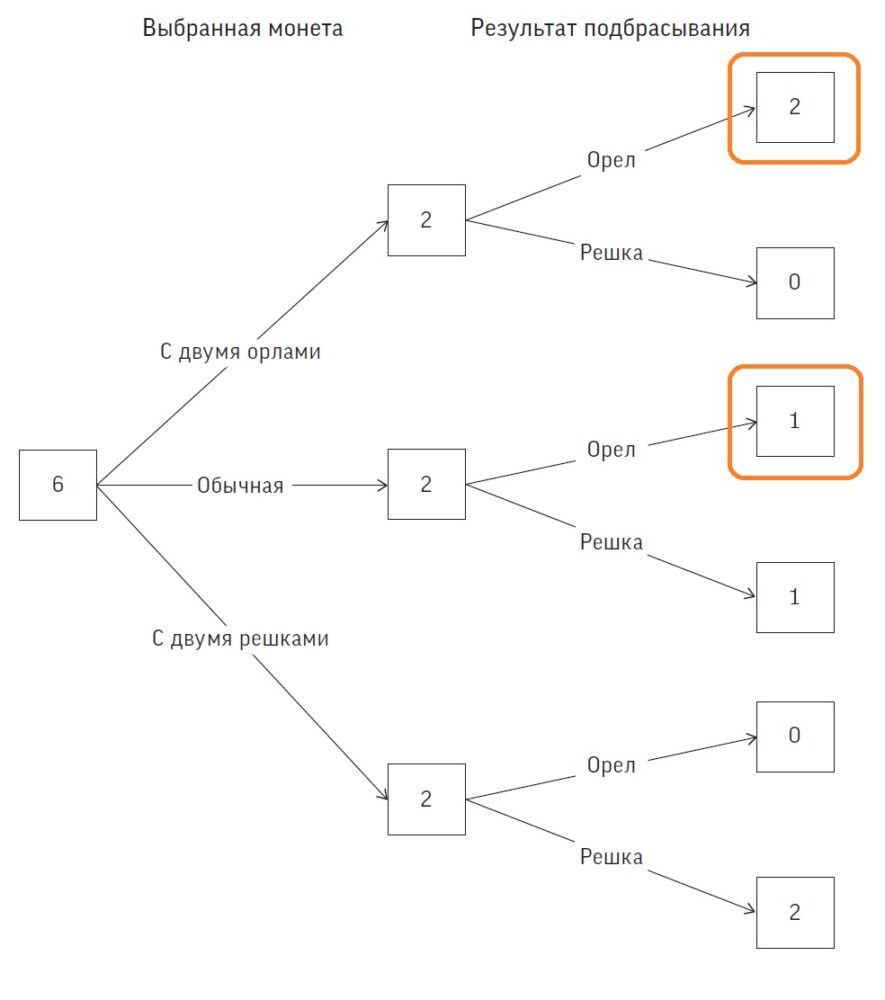
Рис. 2. Дерево ожидаемых количеств для задачи с тремя монетами, показывающее, чего можно ожидать в случае шести экспериментов
Модель в Excel
В ячейке А2 формулой…
=ВЫБОР(СЛМАССИВ(100000;;1;3;ИСТИНА);"ОО";"ОР";"РР")
… я задаю 100 000 «монет» трех типов: орел/орел (ОО), орел/решка (ОР) и решка/решка (РР). Вероятность выбора каждого типа монеты = 1/3.
В ячейке В2 формулой…
=ЕСЛИ(СЛУЧМЕЖДУ(1;2)=1;ЛЕВСИМВ(A2);ПРАВСИМВ(A2))
… я выбираю одну из сторон монеты. Вероятность выбора каждой стороны = ½.
В ячейке Е3 формулой…
=СЧЁТЕСЛИМН(B:B;$E$1;A:A;D3)
… я подсчитываю число монет типа ОР, для которых в результате подбрасывания выпал орел.
Видно, что если выпал орел, то вероятность того, что вторая сторона тоже орел (т.е., выбрана монета ОО) в два раза выше.
Если вам всё еще кажется, что ответ странный, подумайте об этом так. Монета РР имеет ноль шансов выпасть орлом. Монета ОР имеет один шанс из двух выпасть орлом. Монета ОО выпадет орлом в двух шансах из двух. Всего три шанса, что выпадет орел. При этом два шанса, что вторая сторона тоже орел))
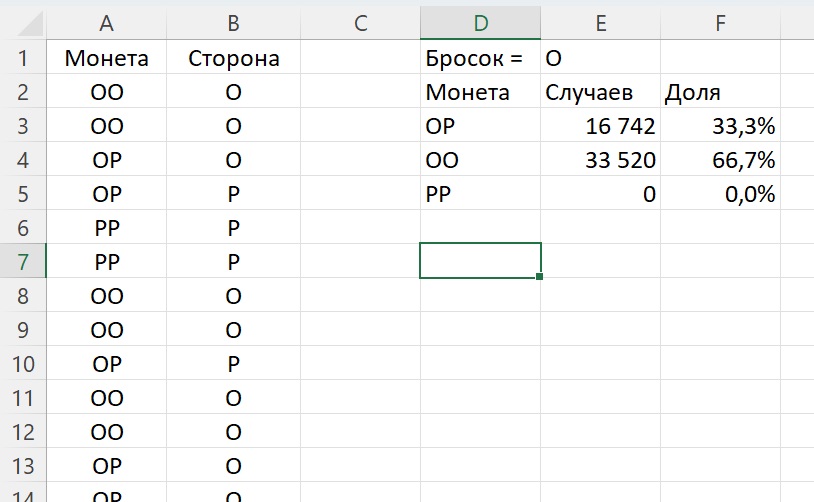
Рис. 3. Модель в Excel
Странная логика.
«Вы наугад вытаскиваете монету, подбрасываете ее, и выпадает орел.
Какова вероятность, что на другой стороне монеты тоже орел?»
Иными словами, вопрос сводится к определению вероятности того,
что из кармана вытащена именно монета с двумя орлами, ибо только
с ней получится такой результат.
Такая монета лишь 1 из 3, => вероятность — 1/3.
Или?
Или))
У нас осталось 2 варианта монеты с орлом, прчём на одной он есть и с обратной стороны, а на другой его нет. Поэтому вероятность — 1/2 🙂
Вот если бы нам выпала решка, тогда вероятность орла 1/3*0 + 1/3*1/2 + 1/3 * 1 = 1/2. Логично, что и в произвольном случае вероятность тоже 1/2. Ситуация сбалансирована.
2 из 3 шансов что выпадет орёл и 1/2 из этих шансов, что орёл окажется и на другой стороне. Значит в итоге 2/6 за то, что при выпавшем орле на другой стороне тоже орёл.
Именно это можно увидеть на картинке: из шести экспериментов два совпадения с условиями задачи.
Ну и в финале сократим дробь и получим 1/3
На самом деле здесь высчитывается не то, будет ли второй орел или нет на обороте после броска (если бы высчитывалось это, то вероятность была 1/2, так как из приемлемых исходов после броска у нас оставались только 2 монеты ОО и ОР), а то, с какой вероятностью мы вытащили!! монету, у которой на другой стороне тоже будет орел. Это тот же Парадокс Монти Холла, только там с открытием дверей была задача, а тут с монетой.
Ты берешь монету (для решения задачи надо вытягивать ОО) с общей вероятностью 1/3. После броска и выпадения Орла, монета с РР и вероятность ее вытягивания из кармана отпадает. Но общая вероятность не становится 50/50. Изначальная вероятность 33% на правильную монету говорит, что в 2 случаях из 3 ты ошибся и вытянул не ОО, а ОР. И что вероятность монеты с ОО составляет 66% или 2/3.
Сам факт броска отсылает нас на то, какую мы достали монету. Короче лучше посмотреть про Парадокс Монти Холла на ютубе, там Кевин Спейси все объяснит)