Нил Дж. Салкинд. Статистика для тех, кто (думает, что) ненавидит статистику

Что объединяет множество людей, начинающих изучать статистику? Они считают, что статистика сложна и запутанна. Нил Салкинд постоянно совершенствует свой курс, и выпустил уже 6-е издание, стремясь так рассказывать о статистике, чтобы новички перестали пугаться! В книге совсем немного теории и доказательств. После прочтения вы сможете понять материал в научных статьях, интерпретировать результаты статистического анализа, а также выполнять основные статистические операции.

В этой книге вы найдете: чем занимается статистика; вычисление и значение средних; что такое дисперсия и стандартное отклонение, надежность и достоверность; зачем нужно иллюстрировать данные; какие существуют типы корреляции; определение вероятности и кривая нормального распределения; как отличать ошибки первого и второго рода; Z- и t-критерии; основы дисперсионного анализа; линейная и множественная регрессия; хи-квадрат и другие непараметрические критерии. Примеры выполнены в статистическом пакете SPSS.

Нил Дж. Салкинд. Статистика для тех, кто (думает, что) ненавидит статистику. – М.: ДМК Пресс, 2020. – 502 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 6% от объема книги), примеры в формате Excel

Купить книгу в Ozon или Лабиринте

Файлы с данными можно скачать на сайте издательства.

Часть I. Ура! У меня статистика

Статистика – наука об организации и анализе информации. С помощью статистики мы можем извлечь смысл из исследований.

Глава 1. Статистика или садистика?

Вы узнаете о сборе, организации и обобщении данных в рамках описательной статистики. А затем, когда познакомитесь с приемами статистики вывода, вы научитесь интерпретировать данные. Описательная статистика занимается организацией и описанием характеристик совокупности данных. Статистика вывода становится следующим методом, который требуется после сбора и обобщения данных. Она позволяет на основании небольшой группы данных сделать выводы о большей группе. Меньшая группа данных часто называется выборкой, и она является частью либо подмножеством генеральной совокупности, или популяции.

Статистика – это инструментарий, который помогает понять мир вокруг нас. Она структурирует собранную информацию и позволяет нам сделать определенные утверждения, насколько характеристики этих данных будут применимы в новых условиях. Есть множество различных способов для обдумывания и решения всевозможных типов задач. Набор инструментов, с которым вы познакомитесь в этой книге, поможет вам посмотреть на интересные задачи с нового ракурса. И хотя это может быть вовсе не очевидно сейчас, но этот новый способ мышления можно будет применять и в новых ситуациях.

Часть II. Σигма, Фрейд и описательная статистика

Глава 2. Серединный мир

Среднее – это одна величина, которая лучше всего отражает целую группу величин. Средние, которые также называются мерами центральной тенденции, представлены тремя видами: среднее значение, медиана и мода. Среднее значение очень чувствительно к экстремальным значениям величин.

Иногда вы можете столкнуться с ситуацией, когда одно и то же значение встречается несколько раз, и тогда вам понадобится рассчитать взвешенную среднюю. Взвешенную среднюю легко посчитать, умножив значения на частоту их появления, сложив все произведения и затем поделив сумму на общее количество случаев.

В основах статистики проводится важное различие между величинами, относящимися к выборке (части генеральной совокупности) и ко всей генеральной совокупности (или популяции) в целом. Для этого статистики прибегают к следующим договоренностям. Для показателей выборки (таких как средняя по выборке) используются латинские буквы. Для параметров генеральной совокупности (таких как средняя по генеральной совокупности) берут греческие буквы. Так, например, среднее значение оценок за контрольную у 100 пятиклассников будет обозначаться Х̅₅, тогда как средняя оценка для генеральной совокупности всех пятиклассников будет обозначаться греческой буквой «мю» – μ₅.

Медиана не чувствительна к крайним значениям, на которые реагирует среднее значение. Когда у вас есть набор величин, в котором одно или несколько значений являются экстремальными, медиана лучше обозначает центральное значение этого набора, чем любая другая мера центральной тенденции.

Мода – это значение, которое встречается в наборе данных чаще всего.

Шкалы измерения можно расставить в порядке от наименее (номинальной) к наиболее тонко настроенной (пропорциональной). Чем «выше» находится шкала измерения, тем точнее, детальнее и информативнее собираемые данные. Средняя точнее измеряет центральную тенденцию, чем медиана, а медиана – точнее, чем мода. Используйте моду, когда имеете дело с категориальными данными, чьи значения могут попадать только в один класс (такими как цвет волос, политические предпочтения, место жительства и религия). В подобных случаях эти категории называются взаимоисключающими.

Используйте медиану, когда имеете дело с выбросами и не хотите исказить средние показатели, например, когда интересующая вас переменная – это доход, выраженный в долларах. Используйте среднюю, когда имеете дело с данными без выбросов, которые при этом не являются категориальными (например, с числовой оценкой за тест или количеством секунд, за которое можно проплыть 50 ярдов).

Глава 3. Vive la Difference!

Изменчивость показывает, насколько отдельные данные отличаются друг от друга. Изменчивость –мера того, насколько каждая величина в группе данных отличается от среднего значения. Размах вычисляется путем вычитания минимального значения распределения из максимального. Размах говорит о том, насколько различаются самое большое и самое маленькое значения в наборе данных. Но размах мало что говорит об отличии друг от друга индивидуальных величин.

Стандартное отклонение отображает среднюю величину изменчивости в наборе данных. Это среднее расстояние от среднего значения:

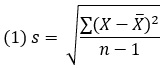
Три важных вопроса, которые улучшат понимание того, что собой представляет стандартное отклонение. Во-первых, почему мы просто не сложили все отклонения от среднего? Мы не сделали этого потому, что сумма всех отклонений от среднего всегда равна нулю. Во-вторых, почему мы возводим отклонения в квадрат? Мы делаем это потому, что хотим избавиться от знаков «минус», чтобы при суммировании не получился ноль. И наконец, почему в итоге мы извлекаем квадратный корень? Мы делаем это потому, что хотим вернуться к тем же единицам измерения, с которых начинали.

Почему n – 1? Что не так с n? Подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?

Глава 4. Лучше один раз увидеть

Способы сделать диаграмму информативной:

• Выберите правильный тип диаграммы
• Минимизируйте. Удалите элементы диаграммы, которые не несут смысловой нагрузки
• Выровняйте заголовок влево
• Дайте говорящее название
• Выровняйте подписи осей вверх и вправо
• Сделайте пропорции, как картинка TV

Столбиковые диаграммы нужно использовать, когда вы хотите сравнить частоты различных категорий между собой. Категории перечисляются по горизонтальной оси х, а значения показываются по вертикальной оси у.

Круговые диаграммы нужно использовать, когда вы хотите показать долю чего-то.

Глава 5. Мороженое и преступность

Коэффициент корреляции – это числовой показатель, который показывает ассоциацию (связь) между двумя переменными. Значение этой описательной статистики находится в пределах от –1 до +1.

Коэффициент корреляции Пирсона между переменными X и Y:

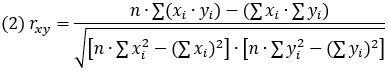
Обратите внимание на сумму квадратов и квадрат суммы. В Excel используется функция КОРРЕЛ().

Что действительно интересно в корреляциях, так это то, что они измеряют расстояние, на котором одна переменная изменяется в соотношении с другой. Так, если обе переменные имеют высокую вариабельность (изменчивость), то корреляция между ними будет скорее высокой, чем низкой. Нельзя утверждать, что большая изменчивость гарантирует высокую корреляцию, поскольку для этого нужно, чтобы изменения значений имели систематический характер. Но если изменчивость одной переменной ограничена, то тогда не важно, как сильно меняется другая, корреляция все равно будет ниже. В предельном случае, когда одна переменная вовсе не меняется r_xy = 0.

Визуально корреляцию представляют диаграммой рассеяния. В Excel такие диаграммы называются точечными.

Как интерпретировать коэффициент корреляции?

Эмпирический метод оценивает «на глазок»:

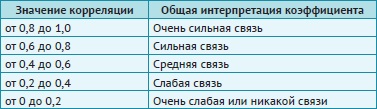
Рис. 1. Интерпретация коэффициента корреляции

Гораздо более точный способ интерпретации коэффициента корреляции – через вычисление коэффициента детерминации. Коэффициент детерминации показывает, сколько процентов дисперсии в одной переменной связано с дисперсией другой переменной. Коэффициент детерминации равен квадрату коэффициента корреляции. Например, если корреляция между средним выпускным баллом и количеством учебных часов равна 0,70 (или r_србалл = 0,70), тогда коэффициент детерминации, обозначаемый r²_србалл, равен 0,7², или 0,49. Это означает, что 49 % дисперсии среднего балла можно объяснить разницей во времени, уделяемом учебе.

Рис. 2. Общая дисперсия и корреляция между переменными

Помните, что корреляция выражает ассоциацию, существующую между двумя или более переменными, при этом она никак не связана с причинностью. Две переменные могут иметь общую причину, которая остается за кадром. Например, была установлена связь: чем больше съедается мороженого, тем… выше преступность. Однако, обе переменные связаны с температурой на улице. Когда становится тепло, совершается больше преступлений… и съедается больше мороженного.

Для разных шкал измерения используются разные коэффициенты корреляции:

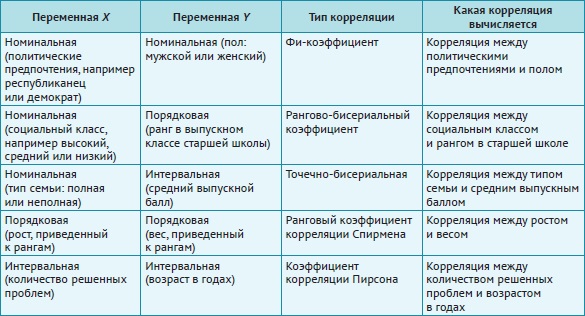
Рис. 3. Шкалы измерения и типы корреляций

Коэффициент частной корреляции показывает степень (тесноту) взаимосвязи двух переменных относительно друг друга, без учета влияния третьей переменной. Иногда третью переменную называют опосредующим (или искажающим) фактором.

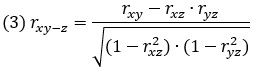
Возвращаясь к предыдущему примеру, допустим данные о потреблении мороженого, уровне преступности и температуре в 10 городах были следующими:

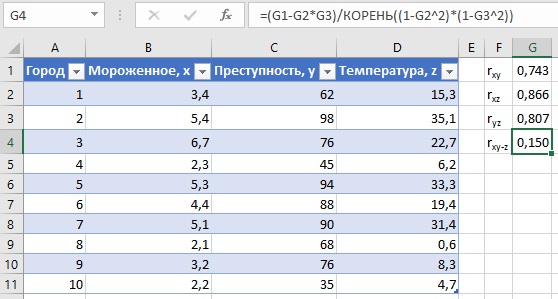
Рис. 4. Пример вычисления коэффициента частной корреляции

После очистки от влияния температуры мы получили коэффициент корреляции между потреблением мороженного и уровнем преступности r_xy-z = 0,15. На уровне шума.

Реальная статистика. Вот забавный материал, соответствующий растущему интересу к применению статистики в спорте с неофициальным названием саберметрика. Термин был придуман Биллом Джеймсом (Bill James) и стал известен благодаря фильму Человек, который изменил все.

Стивен Холл (Stephen Hall) с коллегами исследовал связь между заработком команд и их конкурентоспособностью в профессиональном бейсболе и футболе. Он был одним из первых, кто посмотрел на нее с эмпирической точки зрения. Другими словами, до того, как были опубликованы эти данные, большинство людей принимало решения на основании разрозненного опыта, а не опираясь на количественные оценки. Холл взял данные о заработной плате команд в Главной лиге бейсбола и в английском футболе за период 1980–2000 гг. и использовал для их изучения модель, которая позволяла выявить причинно-следственные связи (а не только ассоциацию).

За 1990-е гг. и оплата, и результаты бейсболистов существенно выросли, но нет доказательств, что причинная связь идет от оплаты к результативности. Для сравнения: исследователи показали, что для английского футбола более высокая оплата стала причиной лучших результатов. Здорово, правда, что можно исследовать ассоциацию при помощи специальных казуальных моделей?

Hall S., Szymanski S. & Zimbalist A. S. Testing causality between team performance and payroll: The cases of Major League Baseball and English soccer. Journal of Sports Economics, 2002. Р. 149-168.

Глава 6. Только правда

Надежность свидетельствует о том, насколько последовательно тест или то, что вы используете в качестве инструмента измерения, измеряет что-то. Поскольку…

Наблюдаемая оценка = истинная оценка + оценка ошибки

…надежность тем выше, чем ниже ошибка.

Различают надежность нескольких видов. Ретестовая надежность применяется, когда вы хотите проверить, надежен ли тест при повторении через какое-то время. Измеряется коэффициентом корреляции Пирсона. Надежность параллельных форм применяется, когда вы хотите проверить эквивалентность, или равнозначность, двух разных форм одного и того же теста. Измеряется коэффициентом корреляции Пирсона. Надежность внутренней согласованности применяется, когда вы хотите знать, согласованы ли между собой элементы теста в том, что они отражают одно (и только одно) измерение, компонент или интересующую область. Измеряется с помощью Альфа Кронбаха.

При вычислении альфы Кронбаха вы рассчитываете корреляцию между баллами каждого элемента и общей суммой баллов по каждому человеку, а затем сравниваете ее с дисперсией всех индивидуальных оценок за отдельные задания. Логика в этом такова, что любой тестируемый с высоким общим баллом должен иметь (более) высокий балл по каждому заданию (например, 5, 5, 3, 5, 3, 4, 4, 2, 4, 5 при общем балле 40), а каждый тестируемый с (более) низким общим баллом будет иметь (более) низкую оценку за каждое отдельное задание (например, 4, 1, 2, 1, 3, 2, 4, 1, 2, 1).

Формула для расчета альфы Кронбаха:

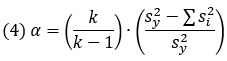
где k – количество вопросов; s²_y – дисперсия каждого наблюдаемого значения; Σs²_i – сумма всех дисперсий для каждого задания.

На рис. 5 представлена выборка ответов 10 людей на вопросы об отношении к медучреждениям. Ответы могли находиться между 1 (полностью несогласен) и 5 (полностью согласен). Также показаны промежуточные вычисления.

Рис. 5. Пример расчета альфа Кронбаха

Взаимная надежность оценивающих – это показатель, который говорит о том, насколько двое оценивающих согласны в своих суждениях о каком-то результате. Измеряется формулой:

(5) Взаимная надежность оценивающих = Количество согласий / Количество возможностей согласия

Достоверность, или валидность, – свойство инструмента оценки, которое показывает: этот инструмент делает именно то, что он обещает сделать. Достоверный тест – это тест, который измеряет то, что планирует измерить.

Процесс установки надежности и достоверности любого инструмента может занять годы напряженной работы. Если вы занимаетесь собственным исследованием, например для диплома или диссертации, обязательно найдите показатель, который уже имеет хорошо обоснованные надежность и достоверность. Таким образом, вы сможете заняться основной работой по тестированию гипотез, а не возиться с труднейшей задачей разработки инструментария, которая сама по себе может стать делом жизни.

Часть III. Карты, деньги, вероятности

Глава 7. Гипотезы и вы

Показатель того, насколько хорошо выборка отображает свойства генеральной совокупности, называется ошибкой репрезентативности. Ошибка репрезентативности – это разница между значениями статистики выборки и параметрами генеральной совокупности. Чем выше ошибка репрезентативности, тем больше погрешность вашей выборки, следовательно, тем сложнее будет доказать, что результаты, полученные для нее, действительно отображают то, что вы ожидали обнаружить в генеральной совокупности. И точно так же, как существуют меры изменчивости для распределений, есть и показатели изменчивости для этой разницы между выборкой и генеральной совокупностью. Она часто называется стандартной ошибкой — по сути, это стандартное отклонение для разницы между показателем выборки и генеральной совокупности.

Нулевая гипотеза – это утверждение об отсутствии разницы между переменными, которые вы изучаете. Например, между учениками 9-го и 12-го классов не будет наблюдаться различий в средних результатах теста на память.

Более того, если между двумя группами обнаружатся различия, вы должны предположить, что они объясняются случайностью.

Альтернативная гипотеза утверждает, что между переменными существует связь. Для одной нулевой гипотезы может быть сформулировано несколько альтернативных. Альтернативные гипотезы бывают направленные или ненаправленные.

Ненаправленная альтернативная гипотеза для примера с учениками описывается уравнением:

где H₁ является обозначением первой (из, возможно, нескольких) альтернативной гипотезы; Х̅₉ обозначает средний балл по тесту памяти для выборки из учеников 9-го класса; Х̅₁₂ обозначает средний балл по тесту памяти для выборки из учеников 12-го класса.

Направленная альтернативная гипотеза уточняет направление этого различия. Например:

Нулевая гипотеза всегда относится к генеральной совокупности, тогда как альтернативные гипотезы всегда относятся к выборке. Мы отбираем выборку участников из большей совокупности. Затем мы пытаемся обобщить результаты, полученные на выборке, на генеральную совокупность. Это процесс вывода.

Нулевые гипотезы всегда записываются греческими буквами, а альтернативные – латинскими.

Критерии качества хорошей гипотезы

Хорошая гипотеза сформулирована как утверждение, а не как вопрос.

Хорошая гипотеза указывает на ожидаемую связь между переменными. Обратите внимание на слово «ожидаемую». Определение ожидаемой связи помогает предотвратить беспорядочное выуживание любого отношения между переменными, которое может обнаружиться в исследовании (что называется «бессистемным подходом»).

Хорошие гипотезы – это проверяемые гипотезы, т. е. содержащие переменные, которые можно измерить.

Глава 8. Нормальны ли ваши кривые?

Нормальные распределения физических величин отличаются по своим показателям центральной тенденции и изменчивости. Для удобства анализа все нормальные распределения приводят к стандартному нормальному распределению путем простой подстановки:

где z – это z-оценка; X – значение физической величины, для которой дается z-оценка; X̅ – среднее значение распределения; s – стандартное отклонение распределения.

z-оценка – это просто количество стандартных отклонений от среднего значения.

Распределения характеризуются четырьмя параметрами: средним значением, изменчивостью, асимметричностью и эксцессом.

Асимметрия – это мера отсутствия симметрии, или скошенности, распределения. Другими словами, один «хвост» распределения длиннее другого. У распределения с положительной асимметрией правый хвост тоньше и длиннее. И наоборот, у распределения с отрицательной асимметрией левый хвост тоньше и длиннее.

Эксцесс показывает степень плоскости или крутизны распределения. Плосковершинным называется более плоское, по сравнению с нормальным, распределение. Крутовершинным называют распределение с более высокой вершиной в центре, по сравнению с нормальным.

Если дисперсия пропорциональна квадрату разности отдельных значений и среднего, асимметрия (скос) – кубу, то эксцесс – четвертой степени:

В Excel для вычисления этих статистик есть функции СКОС() и ЭКСЦЕСС().

Часть IV. Значимая разница: применение статистики вывода

Глава 9. Значимо значимый

Поскольку наш мир не идеален, мы не можем быть уверены в том, что только выделенные нами факторы могут вызывать различия между группами. Уровень случайности, или риска, который вы готовы взять на себя, выражается в виде уровня значимости. Если вы видите, что представленные результаты имеют уровень значимости 0,05 (или p < 0,05), это можно объяснить как наличие 1 шанса из 20, что любые найденные различия объясняются не приведенной в гипотезе причиной, а какой-то другой, неизвестной причиной или причинами (либо случайностью).

В итоге исследователь определяет уровень риска, который он готов взять на себя. Если результаты попадают в область, которая говорит: «Это не могло произойти по чистой случайности — что-то еще оказывает влияние», — то исследователь знает, что нулевая гипотеза (которая утверждает отсутствие различий) не является лучшим объяснением полученных результатов. Вместо нее предпочтительнее использовать объяснение альтернативной гипотезы (заключающееся в том, что существуют различия или неравенство).

Статистическая значимость (формальное определение) – это степень принимаемого вами риска, что вы отклоните нулевую гипотезу, когда в действительности она будет справедлива. Принимаемый вами риск совершить такую ошибку (или уровень значимости) также известен как ошибка первого рода, или ошибка типа I.

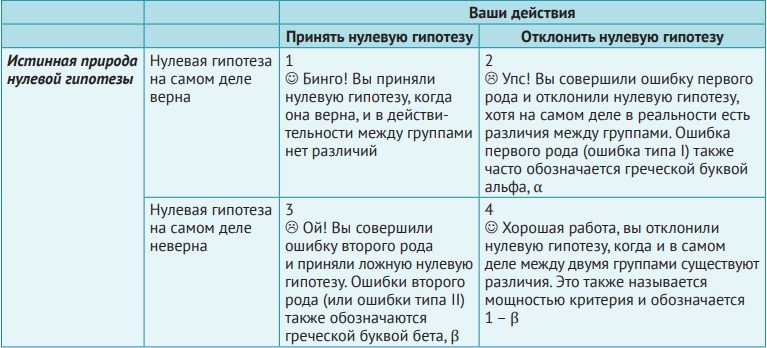
Рис. 6. Различные типы ошибок

Самое важное для понимания этой таблицы – то, что исследователь никогда на самом деле не знает истинной природы нулевой гипотезы и того, есть ли в действительности разница между группами. Почему? Потому что генеральная совокупность (которую представляет нулевая гипотеза) никогда не тестируется напрямую. Это непрактично, и именно поэтому у нас есть статистика вывода.

В идеале вы хотите минимизировать ошибки и первого, и второго рода, но это не всегда легко и не всегда вам подконтрольно. Вы можете полностью контролировать уровень ошибки первого рода или объем риска, который вы готовы принять (потому что фактически сами устанавливаете этот уровень). Ошибки второго рода, однако, не напрямую зависят от вас, но связаны с такими факторами, как размер выборки. Ошибки второго рода особенно чувствительны к количеству предметов в выборке, и по мере возрастания их числа ошибки второго рода сокращаются.

Тогда как описательная статистика применяется для описания характеристик выборки, инференциальная статистика используется для формирования предположений о генеральной совокупности на основании этих характеристик.

Как работает проверка значимости: план

Проверка значимости основана на факте, что с каждым типом нулевой гипотезы связан определенный вид статистики, или статистический критерий. Вот общие шаги, которые нужно предпринять для статистической проверки любой нулевой гипотезы:

• формулировка нулевой гипотезы
• определение уровня значимости, или ошибки первого рода, связанного с нулевой гипотезой
• выбор статистического критерия (рис. 7)
• вычисление значения критерия на основе наших данных
• расчет критического значения, необходимого для отклонения нулевой гипотезы
• сравнение наблюдаемого значения с критическим: если наблюдаемое значение оказывается более крайним, чем критическое, то нулевая гипотеза не может быть принята; если полученное значение не превосходит критического, нулевая гипотеза является самым привлекательным объяснением.

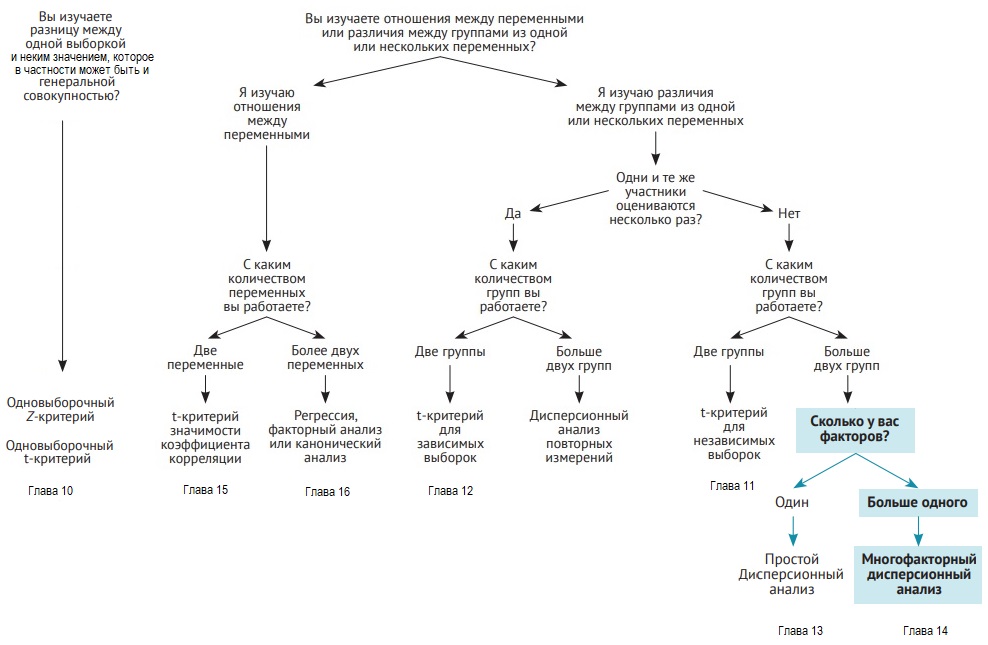
Рис. 7. Быстрая (но не всегда идеальная) инструкция для выбора применяемого статистического критерия; ; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

На рис. 8 представлены все шаги, которые мы только что сделали. Кривая отображает все возможные результаты для конкретной нулевой гипотезы, такие как различия между двумя группами или значимость коэффициента корреляции. Критическое значение – это точка, после которой наблюдаемые значения считаются такими редкими, что делается вывод: наблюдаемые значения возникли не случайно, а из-за влияния какого-то фактора. Если результат, представленный наблюдаемым значением, оказывается слева от критической точки, то делается вывод, что нулевая гипотеза является наиболее привлекательным объяснением для любых наблюдаемых различий. Если наблюдаемое значение оказывается справа от критической точки, то делается вывод, что альтернативная гипотеза является наиболее привлекательным объяснением для любых наблюдаемых различий.

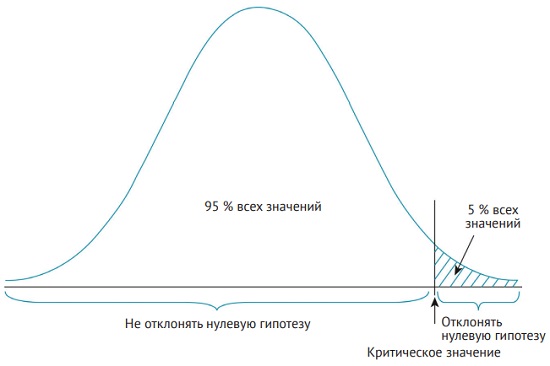
Рис. 8. Сравнение наблюдаемых значений с критическими и решение об отклонении или принятии нулевой гипотезы

Глава 10. Строго по одному. Одновыборочный Z-критерий

Если мы изучаем различия между выборкой и генеральной совокупностью, т.е., проверяется только одна группа, то подходящий статистический критерий – это одновыборочный Z-критерий.

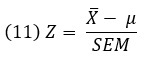
где X̅ – среднее значение выборки; µ – среднее значение совокупности; SEM – стандартная ошибка среднего.

А теперь для расчета стандартной ошибки среднего, которая нужна вам в формуле 10.1, воспользуйтесь формулой 10.2:

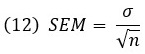
где σ – стандартное отклонение генеральной совокупности; n – размер выборки.

Рассмотрим пример. Д-р МакДональд думает, что его группа студентов, изучающих науку о Земле, исключительна (в хорошем смысле), и ему интересно знать, попадает ли средняя оценка его группы в границы средних оценок большей группы студентов, изучавших науку о Земле за прошедшие 20 лет. Он знает средние значения и стандартные отклонения как для своей группы из 36 человек, так и для большей группы из 1000 бывших учеников:

Рис. 9. Показатели студентов

Нулевая гипотеза утверждает, что среднее выборки равно среднему по генеральной совокупности: Н₀: Х̅=µ. Альтернативная гипотеза для данного примера: Н₁: Х̅≠µ. Выберем уровень значимости α=0,05. Используем одновыборочный Z-критерий. Рассчитаем значение статистического критерия (наблюдаемого значения):

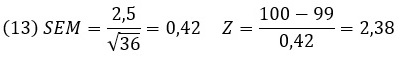
Рассчитаем критическое значение Z-статистики в Excel: =НОРМ.СТ.ОБР(0,975)=1,96. Наблюдаемое значение Z=2,38 попадает в хвост распределения (больше критического). Это означает, что нам нужно дать объяснение, почему различаются средние по выборке и по совокупности. Т.е., отличия нельзя объяснить лишь случайностью.

Размер эффекта

Это мера того, насколько отличаются две группы друг от друга (мера величины воздействия). На размер эффекта не влияет размер выборки. Суждение о размере эффекта добавляет новое измерение к пониманию значимости результатов. Великим гуру размера эффекта был Джейкоб Коэн (Jacob Cohen). d Коэна для размера эффекта одновыборочного Z-критерия:

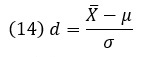
где X̅ – среднее значение выборки; µ – среднее значение генеральной совокупности; σ – стандартное отклонение генеральной совокупности.

Если мы подставим в формулу 14 данные д-ра МакДональда, то получим

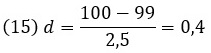
Коэн считал, что

• маленький размер эффекта находится в пределах от 0 до 0,2;
• средний размер эффекта находится в пределах от 0,2 до 0,5;
• большой размер эффекта – это любое значение больше 0,5.

Подробнее см. Джейкоб Коэна Statistical Power Analysis for the Behavioral Sciences.

Если выборки небольшие лучше применить одновыброчный t-критерий, который сравнивает среднее значение выборки с другим значением. Иногда это значение действительно оказывается средним значением генеральной совокупности… но не обязательно.

Глава 11. (t)eт-a-тeт. Проверки значимости для средних значений разных групп

t-критерий Стьюдента для независимых средних:

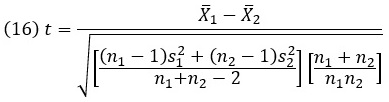
где X̅₁ – среднее значение для группы 1; X̅₁ – среднее значение для группы 2; n₁ — количество участников в группе 1; n₂ — количество участников в группе 2; s²₁ – дисперсия для группы 1; s²₂ – дисперсия для группы 2.

Если n₁=n₂ и дисперсии близки, формула (16) упрощается:

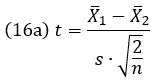
Глава 12. (t)eт-a-тeт (снова). Сравнение средних величин связанных групп

t-критерий для зависимых средних указывает, что одна группа с одними и теми же участниками изучалась в разных условиях (например, до начала эксперимента и после его завершения). Синоним зависимых групп – повторные измерения. t-критерий для зависимых средних:

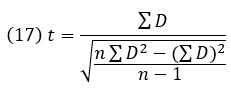
где D – это разность значений конкретного показателя в точке 1 и точке 2; ΣD – сумма всех разностей между группами значений; (ΣD)² – сумма квадратов разностей между группами значений; n –количество пар наблюдений.

Рассмотрим эксперимент, в котором изучались оценки за чтение до и после окончания программы обучения. Нулевая гипотеза Н₀: µ_{после программы}=µ_{до программы}. Альтернативная гипотеза Н₁: µ_{после программы}>µ_{до программы}.

Рис. 10. Оценки за чтение до и после программы

Уровень значимости α=0,05. Мы используем t-критерий для зависимых средних, также называемый t-критерий для парных выборок. Расчет значения статистического критерия (наблюдаемого значения).

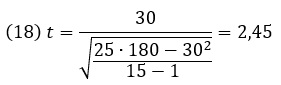
t_{критическое}=СТЬЮДЕНТ.ОБР(0,95;B29-1) = 1,71. Альтернативная гипотеза направленная – результаты эксперимента будут выше, чем до него. Все 5% сосредоточены в одном хвосте t-распределения. Наблюдаемое значение (2,45) больше, чем критическое значение (1,71), что позволяет отклонить нулевую гипотезу.

Глава 13. Двух групп недостаточно? Попробуйте дисперсионный анализ

Если мы проверяем различия между показателями разных групп (например, разницу в результатах спортсменов), спортсмены тестируются только один раз, выделяются три группы (меньше 6 лет опыта, 7-10 лет, более 10 лет опыта), в качестве статистического критерия следует использовать дисперсионный анализ или ANOVA (от англ. ANalysis Of VAriance).

Статистическим критерием для ANOVA является F-критерий (названный в честь Р.А.Фишера, создателя этого критерия).

Простой дисперсионный анализ применяется, когда изучается только один фактор (такое как принадлежность к конкретной группе), причем у этого фактора более двух уровней. Простой дисперсионный анализ также называют однофакторным дисперсионным анализом. Методика называется «дисперсионным анализом», потому что дисперсия, возникающая из-за различий в результатах, подразделяется на (а) дисперсию, возникающую из-за различий между группами, и (б) дисперсию, возникающую из-за различий внутри групп. Затем два вида дисперсий сравниваются друг с другом. Дисперсия между группами объясняется разницей влияния, тогда как внутригрупповая дисперсия возникает из-за различий между отдельными представителями внутри каждой группы.

Более сложный вид дисперсионного анализ, многофакторный, применяется для изучения нескольких экспериментальных факторов. Например, принадлежность к группе и полу.

Рис. 11. Дизайн многофакторного эксперимента

Такой дизайн называется факторным дизайном 3*2. Цифра 3 указывает, что у одного фактора выделяются три уровня (группа 1, группа 2 и группа 3). Цифра 2 указывает, что у другого фактора имеется два уровня (мужской или женский). Их комбинация дает шесть возможных вариантов.

Вычисление статистического критерия Фишера

F-критерий оценивает гипотезы о существовании различий между группами:

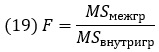
где МS_межгр – дисперсия между группами; MS_{внутригр} – дисперсия внутри групп.

Если бы внутри каждой группы изменчивость отсутствовала, тогда любые различия между группами были бы существенными. F сравнивает степень вариабельности между группами (возникающую из-за группирующего фактора) со степенью вариабельности внутри групп (возникающую вследствие случайности). Если это F = 1, любые различия между группами не являются статистически значимыми. По мере увеличения F возрастает вероятность того, что между группами есть нечто, помимо случайности.

Например, мы изучаем три группы дошкольников и их показатели развития речи (область В1:D11):

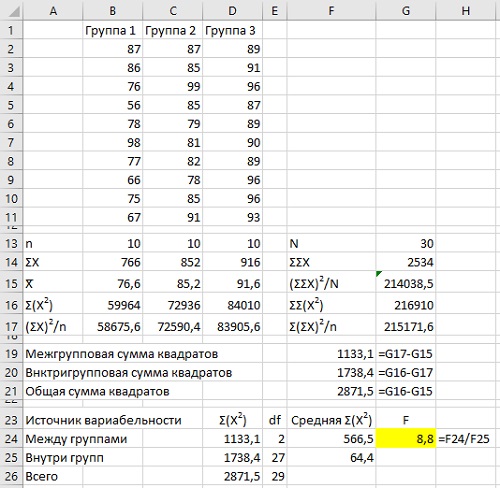
Рис. 12. Показатели развития речи у дошкольников

Нулевая гипотеза утверждает, что нет различий между средними показателями трех групп: Н₀: µ₁=µ₂=µ₃. Альтернативная гипотеза ненаправленная и утверждает, что между средними величинами трех групп существует различия Н₁: Х̅₁≠Х̅₂≠Х̅₃. Выбираем величину ошибки первого рода α=0,05. В качестве статистического критерия выбираем простой дисперсионный анализ.

Ранее мы говорили об одно- и двусторонних критериях. Для дисперсионного анализа такого понятия не существует. Поскольку проверяется больше двух групп и F-критерий является универсальным устойчивым критерием (следовательно, дисперсионный анализ любого вида проверяет общие различия между средними), обсуждение конкретного направления этих различий не имеет смысла.

Предварительно мы вычисляем количество участников в каждой группе (n), сумму значений (ΣX), среднее (X̅), сумму квадратов Σ(Х²) и среднюю сумму квадратов (ΣХ)²/n. Далее вычисляем аналогичные показатели для всех трех групп (область F13:G17). Теперь можно вычислить межгрупповую, внутригрупповую и общую сумму квадратов (область F19:F21).

На следующем этапе нужно определиться со степенями свободы для трех сумм квадратов. Для межгрупповой оценки df=k–1, где k – количество групп. Для внутригрупповой оценки df =N–k, где N – размер всей выборки. Тогда отношение Фишера – это отношение средней суммы квадратов межгрупповых различий к средней сумме квадратов внутригрупповых различий (область D24:G26).

Выполнив эти расчеты вручную, вы получили важное понимание того, откуда берутся цифры, и что они означают. В Excel расчеты можно упростить с помощью надстройки Пакет анализа. Чтобы запустить вычисления пройдите по меню Данные –> Анализ данных. Выберите Однофакторный дисперсионный анализ:

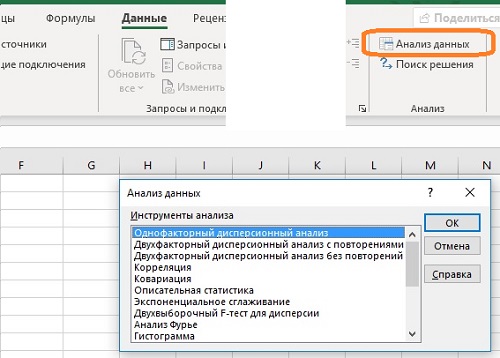
Рис. 13. Запуск надстройки Пакет анализа

Если вы не видите на ленте опцию Анализ данных, пройдите по меню Файл –> Параметры. Перейдите на вкладку Надстройки, и в нижней части окна выберите Надстройки Excel. Нажмите на кнопку Перейти. В открывшемся окне поставьте галочку напротив Пакет анализа.

В окне настроек Однофакторного дисперсионного анализа установите следующие параметры:

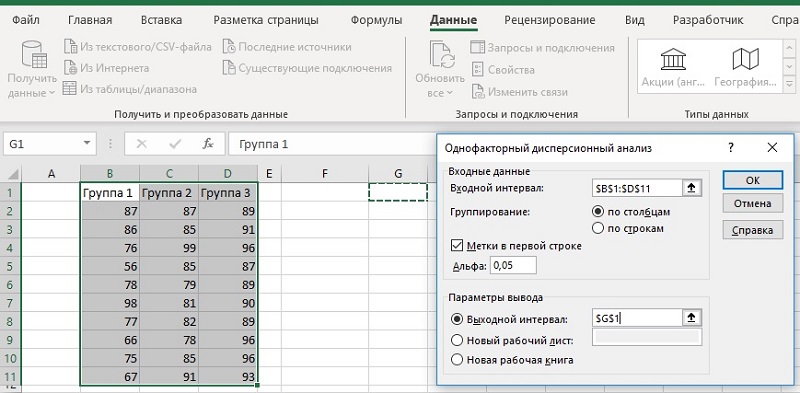
Рис. 14. Настройка опций Однофакторного дисперсионного анализа

Нажмите Ok. На листе Excel появится таблица:

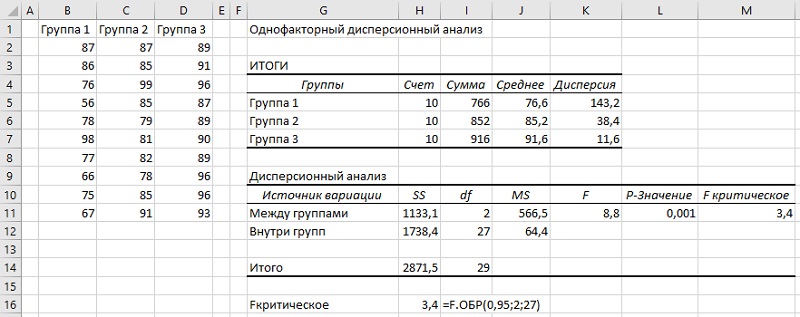
Рис. 15. Однофакторный дисперсионный анализ с помощью надстройки Пакет анализа

Значения в таблице, естественно, не отличаются от предыдущих ручных расчетов (сравни с рис. 12).

Любопытно, что F-критерий для двух групп будет равен квадрату t-критерия для двух групп: F = t².

Как и раньше, нам нужно сравнить наблюдаемое F-значение с критическим. Критическое F-значение можно найти в Интернете (например, здесь). Оно также выводится в таблице Однофакторного дисперсионного анализа – см. ячейку М12 на рис. 15. F-значение также можно рассчитать с помощью формулы =F.ОБР(0,95;2;27). Здесь 0,95 = 1–α, 2 – число степеней свободы в числителе, 27 – в знаменателе.

Наблюдаемое значение (8,8) больше критического (3,4), следовательно нулевую гипотезу нельзя принять. Различия между группами не могли появиться случайно, а стали следствием влияющего фактора – метода обучения чтению.

Можно сравнить еще два значения: вероятность того, что наблюдаемые различия – следствие случайности и уровень значимости α. Первая вероятность рассчитана на рис. 15 в ячейке L11 и равна 0,001. Это существенно меньше α=0,05.

Размер эффекта для однонаправленного дисперсионного анализа

Здесь используется величина под названием «эта в квадрате» η². Шкала для оценки размера эффекта: маленький – около 0,01; средний – около 0,06; большой – около 0,14.

Наблюдаемый размер эффекта является большим.

Установив, что различия средних существуют, вы можете выяснить, какие именно средние различаются. Стандартного метода в Excel я не нашел. Есть опция в SPSS (подробнее см. Апостериорные критерии для однофакторного дисперсионного анализа).

Глава 15. Двоюродные или просто хорошие друзья? Проверка отношений коэффициентом корреляции

Если вы изучается связь между переменными (а не различия между группами), используются только две переменные, то подходящая статистика – t-критерий для коэффициента корреляции. Рассмотрим, например, связь между качеством брака и качеством детско-родительских отношений. Эти (придуманные) значения находятся в диапазоне от 0 до 100. Чем выше показатель, тем брак счастливее, а отношения с детьми лучше.

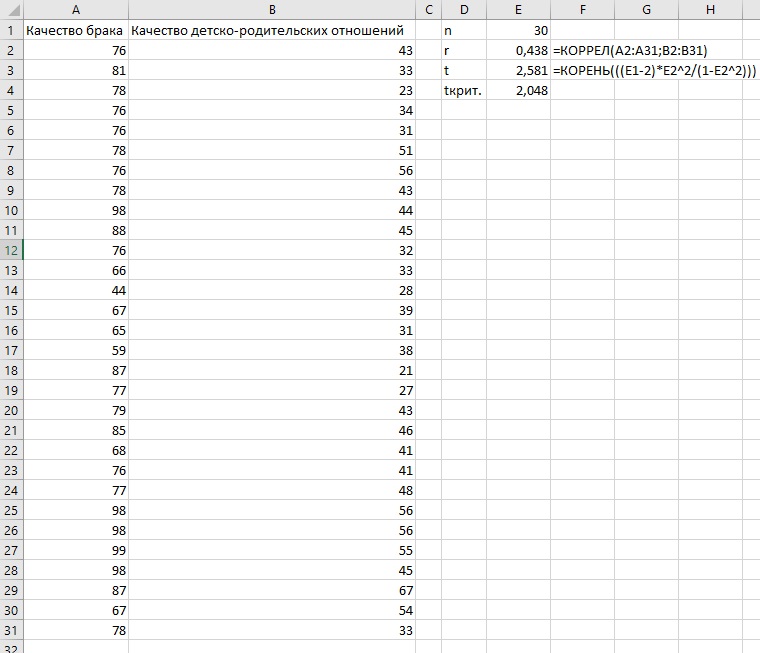
Рис. 16. Качество брака и отношений с детьми

Коэффициент корреляции Пирсона r = 0,438. А теперь пройдем по всем этапам проверки значимости и принятия решения о смысле этой величины.

Нулевая гипотеза утверждает отсутствие связи между качеством брака и качеством отношений между родителями и детьми Н₀: ρ_xy = 0. Греческая буква ρ обозначает оценку коэффициента корреляции для генеральной совокупности. Альтернативная гипотеза является двусторонней и утверждает наличие взаимосвязи между двумя переменными Н₁: r_xy ≠ 0. Уровень значимости α = 0,05. t-критерий для коэффициента корреляции:

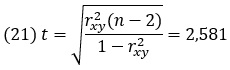
t_{критическое} = СТЬЮДЕНТ.ОБР.2Х(α;n-2) = СТЬЮДЕНТ.ОБР.2Х(0,05;30-2) = 2,048

t > t_{критическое}, и у нас есть основания отклонить нулевую гипотезу.

Глава 16. Как предсказать, кто выиграет Суперкубок. Применение линейной регрессии

Что такое предсказание?

Вы можете не только рассчитать степень, в которой две переменные связаны между собой (путем вычисления коэффициента корреляции), но и использовать эти корреляции для того, чтобы предсказать значение одной переменной на основании значения другой. Как работает регрессия? Собираются данные о прошлых событиях (например, о существующей связи между двумя переменными), а затем они применяются к будущему событию при условии знания только одной переменной. Чем выше абсолютное значение коэффициента корреляции, тем точнее будет предсказание.

Рассмотрим пример предсказания среднего балла в колледже на основании среднего балла аттестата.

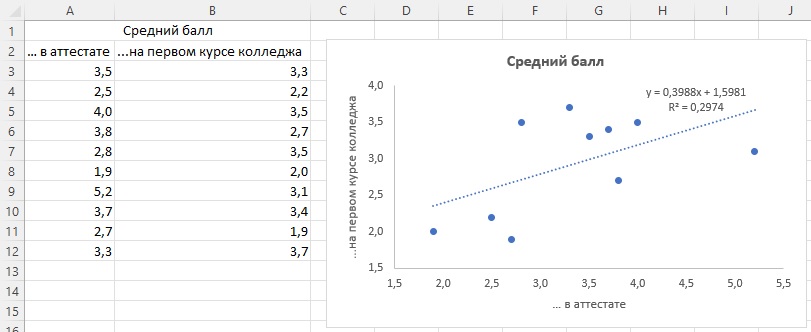
Рис. 17. Средний балл в аттестате и на первом курсе колледжа

Начните с построения диаграммы рассеяния исходных данных (область А2:В12). Кликните правой кнопкой мыши на любую точку на диаграмме и выберите Добавить линию тренда. Это и есть линии регрессии. Кликните на линию тренда, справа появится окно Формат линии тренда. Поставьте галочки Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R²). Линия регрессия строится методом наименьших квадратов. Она проходит так, чтобы сумма квадратов расстояний от реальных точек до линии (по вертикали) была наименьшей.

Показателем ошибки регрессии является коэффициент детерминации. Он показывает процент снижения ошибки в отношениях между переменными. В нашем примере корреляция между двумя переменными равна 0,55, а коэффициент детерминации – 0,2974 (или 0,55²). Если бы корреляции не было и точки располагались случайной, то R²=0. Сейчас же почти 30% разброса можно объяснить связью двух переменных.

ЧАСТЬ V. Больше статистики! Больше инструментов!

Глава 17. Что делать с ненормальными. Хи-квадрат и другие непараметрические критерии

Изученные ране статистические критерии предполагают, что данные имеют определенные характеристики. Например, что выборка достаточно велика, чтобы быть репрезентативной для генеральной совокупности; что дисперсии обеих групп гомогенны, или одинаковы. Более того, многие из рассмотренных критериев продолжают работать даже в том случае, если одно из этих предположений нарушено. С другой стороны, если предположения нарушены, лучше применять непараметрические критерии.

Хи-квадрат – непараметрический критерий, который позволяет определить, можно ли объяснить наблюдаемое распределение частот чистой случайностью. Одновыборочный хи-квадрат включает в себя только одно измерение и часто называется критерием согласия. Он показывает, насколько собранные вами данные согласуются с паттерном, который вы ожидали увидеть. Двухвыборочный хи-квадрат включает в себя два измерения и часто называется критерием независимости. Например, его можно использовать для проверки того, является ли предпочтение школьных ваучеров независимым от принадлежности к политической партии и пола.

Одновыборочный критерий согласия хи-квадрат

Одновыборочный критерий согласия хи-квадрат сравнивает то, что мы наблюдаем, с тем, что мы ожидали бы от случайности:

где χ² – значение критерия хи-квадрат; О – наблюдаемая частота; Е – ожидаемая частота.

Например, получено три варианта ответов о предпочтении школьных ваучеров:

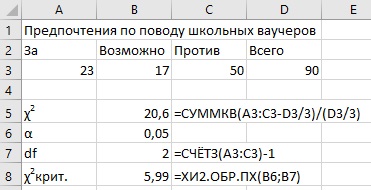
Рис. 18. Предпочтения по поводу школьных ваучеров

Нулевая гипотеза утверждает, что нет различий в частоте распределения случаев по каждой категории H₀: P₁ = P₂ = P₃. Здесь P – процент случаев в категории. Альтернативная гипотеза утверждает, что в частоте распределения случаев по каждой категории есть различия H₁: P₁ ≠ P₂ ≠ P₃. Выберем уровень значимости α = 0,05. В качестве статистического критерия выберем хи-квадрат. Наблюдаемое значение оказывается более крайним, чем критическое. Нулевую гипотезу нельзя принять. Распределение респондентов по группам неравномерно. Определенно, существуют различия в количестве людей, голосующих за, против или не определившихся по вопросу школьных ваучеров.

Почему «критерий согласия»? Название предполагает, что эта статистика отвечает на вопрос, насколько хорошо набор данных согласуется с существующим стандартом. Набор данных – это то, что вы наблюдаете. Слово «согласуется» предполагает, что есть другой набор данных, с которым можно сравнить наблюдаемый. Этот стандарт является набором ожидаемых частот, которые рассчитываются в процессе вычисления значения χ². Если набор данных согласуется с ним, то значение χ² приближается к тому, что вы ожидаете увидеть при влиянии чистой случайности, и не имеет значимых отличий от него. Если наблюдаемые данные не согласуются, тогда то, что вы наблюдаете, отличается от того, что вы могли бы ожидать.

Критерий независимости хи-квадрат

Проверяет наличия связи между двумя измерениями, заданными номинальными переменными. Рассмотрим выборку мужчин и женщин, участвовавших в голосовании.

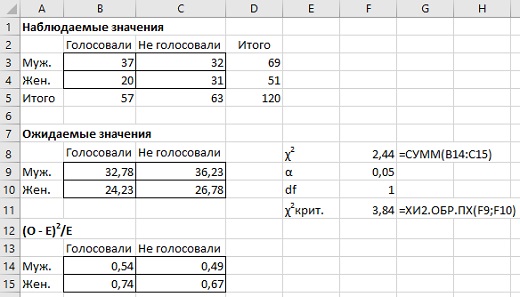
Рис. 19. Участие в голосовании

χ² рассчитывается по формуле (22). Теперь ожидаемое значение – это произведение итога по ряду на итог по столбцу, деленное на общее количество всех наблюдений. Так, например, ожидаемое значение для голосовавших мужчин =(69 × 57)/120 = 32,78. Расчетное χ² = 2,44.

Нулевая гипотеза: пол и участие в голосовании не зависят друг от друга. Альтернативная гипотеза: пол и участие в голосовании зависят друг от друга. Уровень значимости α=0,05. Количество степеней свободы df=(r–1)*(c–1), где r – количество рядов, c – количество столбцов. В нашем примере df=1. Критическое значение χ²крит.=ХИ2.ОБР.ПХ(α;df)=3,84. Если наблюдаемое значение не превосходит критического, то нулевая гипотеза дает самое привлекательное объяснение.

Другие непараметрические критерии

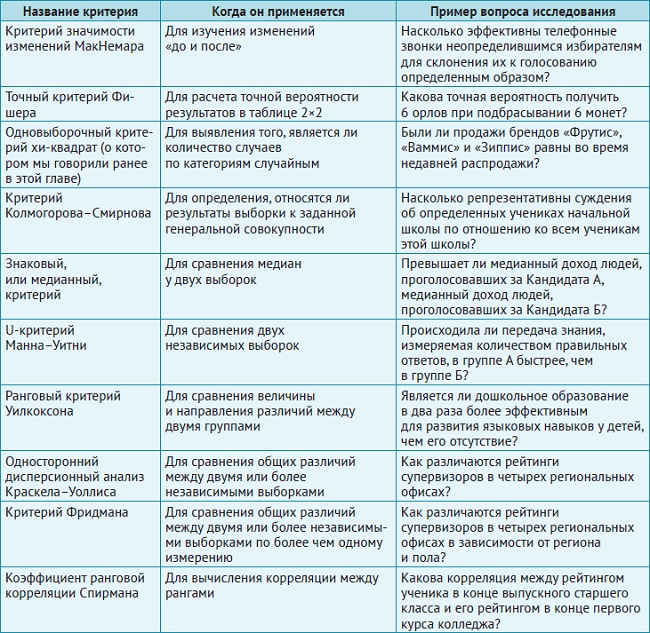
Рис. 20. Непараметрические критерии для анализа категориальных и порядковых данных

Статистические пакеты

Статистическое программное обеспечение https://en.wikipedia.org/wiki/List_of_statistical_software

Бесплатные статистические программы. https://freestatistics.altervista.org/?p=stat

Одна из лучших бесплатных программ (мало в чем уступающая SPSS) – OpenStat https://openstat.en.softonic.com/

Популярная программа – R – см., например? Алексей Шипунов. Наглядная статистика. Используем R http://baguzin.ru/wp/?p=14666

Компания «StatSoft» (принадлежащая «Делл») предлагает семейство продуктов STATISTICA: http://statsoft.ru/

SPSS является одним из самых популярных первоклассных статистических пакетов, и поэтому мы посвятили ему целое приложение в книге: https://baguzin.ru/wp/?p=23334

Интернет-сайты

The World Wide Web Virtual Library: Statistics. Виртуальная библиотека статистики.

История статистики на англ. языке. History of statistics Википедия, eMathZone.

Онлайн-курс из 18 уроков

Данные, готовые к скачиванию:

• наборы статистических данных на https://itl.nist.gov/div898/strd/
• данные Бюро переписи населения США https://census.gov/
• библиотека данных The Data and Story Library https://dasl.datadescription.com/
• наборы данных в области экономики http://www.bris.ac.uk/Depts/Economics/Growth/datasets.htm
• сайт Федерального комитета по статистической методологии США https://nces.ed.gov/FCSM/index.asp