Задачи прогнозирования построены на изменении неких данных во времени (продаж, спроса, поставок, ВВП, выбросов углерода, численности населения…) и проецировании этих изменений на будущее. К сожалению, выявленные на исторических данных, тренды могут нарушаться множеством непредвиденных обстоятельств. Так что данные в будущем могут существенно отличаться от произошедшего в прошлом. [1] В этом и состоит проблема прогнозирования.
Однако, существуют методики (под названием экспоненциальное сглаживание), позволяющие не только попытаться предсказать будущее, но и выразить численно неопределенность всего, что связано с прогнозом. Численное выражение неопределенности с помощью создания интервалов прогнозирования поистине неоценимо, но часто игнорируется в прогностическом мире.
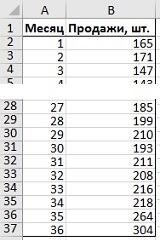
Рис. 1. Временной ряд данных
Скачать заметку в формате Word или pdf, примеры в формате Excel
Исходные данные
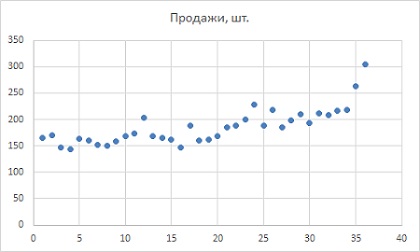
Допустим, вы фанат «Властелина Колец», и вот уже три года изготавливаете и торгуете мечами (рис. 1). Отобразим продажи графически (рис. 2). За три года спрос удвоился — может быть, это тренд? Мы вернемся к этой мысли чуть позже. На графике есть несколько пиков и спадов, что может быть признаком сезонности. В частности, пики приходятся на месяцы с номерами 12, 24 и 36, которые оказываются декабрями. Но может быть это лишь случайность? Давайте выясним.
Рис. 2. Диаграмма временного ряда данных
Простое экспоненциальное сглаживание
Методы экспоненциального сглаживания основываются на прогнозировании будущего по данным из прошлого, где более новые наблюдения весят больше, чем старые. Такое взвешивание возможно благодаря константам сглаживания. Первый метод экспоненциального сглаживания, который мы опробуем, называется простым экспоненциальным сглаживанием (ПЭС, simple exponential smoothing, SES). Он использует лишь одну константу сглаживания.
При простом экспоненциальном сглаживании предполагается, что ваш временной ряд данных состоит из двух компонентов: уровня (или среднего) и некоей погрешности вокруг этого значения. Нет никакого тренда или сезонных колебаний — есть просто уровень, вокруг которого колеблется спрос, тут и там окруженный небольшими погрешностями. Отдавая предпочтение более новым наблюдениям, ПЭС может явиться причиной сдвигов этого уровня. Говоря языком формул,
Спрос в момент времени t = уровень + случайная погрешность около уровня в момент времени t
Так как же найти приблизительное значение уровня? Если принять все временные значения как имеющие одинаковую ценность, то следует просто вычислить их среднее значение. Однако, это плохая идея. Следует дать больший вес недавним наблюдениям.
Создадим несколько уровней. Рассчитаем исходный уровень в первый год:
уровень0 = среднее значение спроса за первый год (месяцы 1-12)
Для спроса на мечи он равен 163. Мы используем уровень0 (163) как прогноз спроса на месяц 1. Спрос в месяц1 равен 165, то есть он на 2 меча выше уровня0. Стоит обновить приближение исходного уровня. Уравнение простого экспоненциального сглаживания:
уровень1 = уровень0 + несколько процентов × (спрос1 – уровень0)
уровень2 = уровень1 + несколько процентов × (спрос2 – уровень1)
И т.д. «Несколько процентов» — называется константой сглаживания, и обозначается альфой. Это может быть любое число от 0 до 100% (от 0 до 1). Выбирать значение альфы вы научитесь позже. В общем случае значение для разных моментов времени:
Уровеньтекущий период = уровеньпредыдущий период +
альфа × (спрос текущий период – уровень предыдущий период)
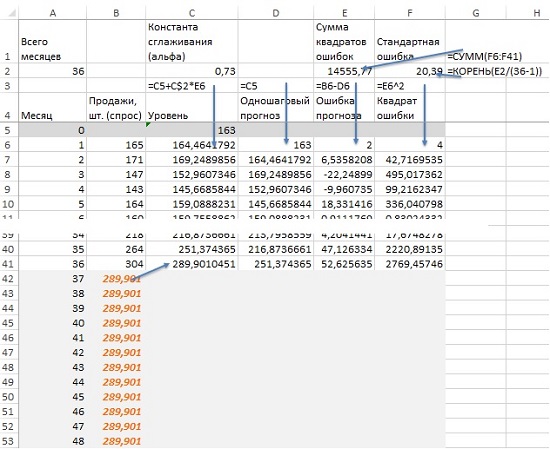
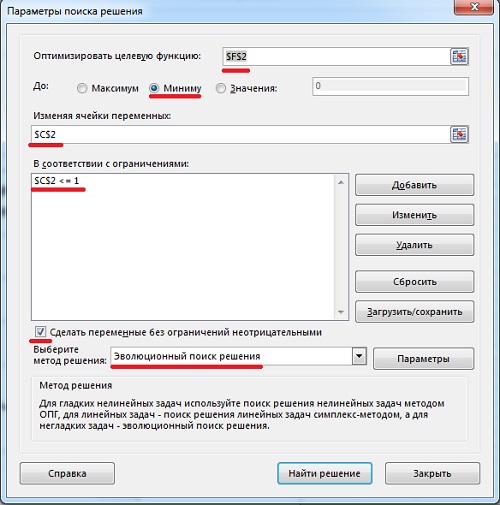
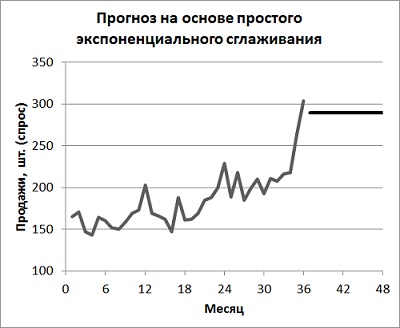
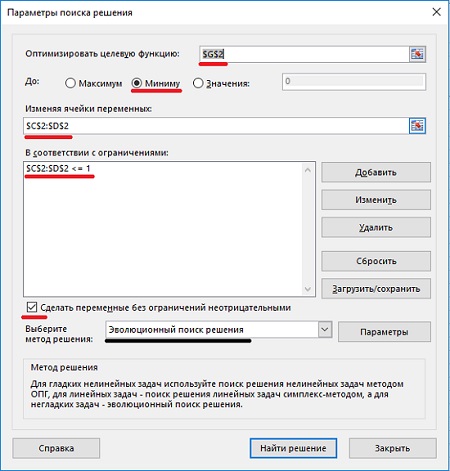
Будущий спрос равен последнему вычисленному уровню (рис. 3). Поскольку вы не знаете, чему равна альфа, установите для начала в ячейке С2 значение 0,5. После того, как модель будет построена, найдите такую альфа, чтобы сумма квадратов ошибки – Е2 (или стандартное отклонение – F2) были минимальны. Для этого запустите опцию Поиск решения. Для этого пройдите по меню ДАННЫЕ –> Поиск решения, и установите в окне Параметры поиска решения требуемые значения (рис. 4). Чтобы отразить результаты прогноза на диаграмме, для начала выберите диапазон А6:В41, и постройте простую линейную диаграмму. Далее кликните на диаграмме правой кнопкой мыши, выберите опцию Выбрать данные. В открывшемся окне создайте второй ряд и вставьте в него предсказания из диапазона А42:В53 (рис. 5).
Рис. 3. Простое экспоненциальное сглаживание
Рис. 4. Параметры поиска решения
Рис. 5. Диаграмма прогноза простого экспоненциального сглаживания
Возможно, у вас есть тренд
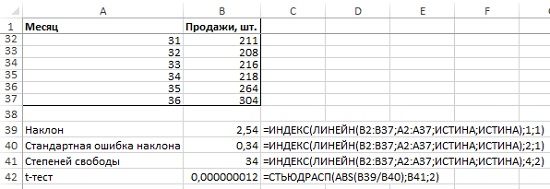
Чтобы проверить это предположение достаточно подогнать линейную регрессию под данные спроса и выполнить тест на соответствие критерию Стьюдента на подъеме этой линии тренда (как в главе 6). Если уклон линии ненулевой и статистически значимый (в проверке по критерию Стьюдента величина р менее 0,05), у данных есть тренд (рис. 6).
Рис. 6. Тест Стьюдента показывает наличие тренда
Мы воспользовались функцией ЛИНЕЙН, которая возвращает 10 описательных статистик (если вы ранее не пользовались этой функцией, рекомендую Функция массива ЛИНЕЙН) и функцией ИНДЕКС, которая позволяет «вытащить» только три требуемые статистики, а не весь набор. Получилось, что наклон равен 2,54, и он значим, так как тест Стьюдента показал, 0,000000012 существенно меньше 0,05. Итак, тренд есть, и осталось включить его в прогноз.
Экспоненциальное сглаживание Холта с корректировкой тренда
Часто оно называется двойным экспоненциальным сглаживанием, потому что имеет не один параметр сглаживания — альфа, а два. Если у временной последовательности линейный тренд, то:
спрос за время t = уровень + t × тренд + случайное отклонение уровня в момент времени t
Экспоненциальное сглаживание Холта с корректировкой тренда имеет два новых уравнения, одно — для уровня по мере его продвижения во времени, а другое — тренд. Уравнение уровня содержит сглаживающий параметр альфа, а уравнение тренда – гамма. Вот как выглядит новое уравнение уровня:
уровень1 = уровень0 + тренд0 + альфа × (спрос1 – (уровень0 + тренд0))
Обратите внимание, что уровень0 + тренд0 — это просто одношаговый прогноз от исходных значений к месяцу 1, поэтому спрос1 – (уровень0 + тренд0) — это одношаговое отклонение. Таким образом, основное уравнение приближения уровня будет следующим:
уровеньтекущий период = уровеньпредыдущий период + трендпредыдущий период + альфа × (спростекущий период – (уровень предыдущий период) + трендпредыдущий период))
Уравнение обновления тренда:
трендтекущий период = трендпредыдущий период + гамма × альфа × (спростекущий период – (уровень предыдущий период) + трендпредыдущий период))
Холтовское сглаживание в Excel аналогично простому сглаживанию (рис. 7), и, как и выше, цель – найти два коэффициента, минимизируя сумму квадратов ошибок (рис. 8). Чтобы получить исходные значения уровня и тренда (в ячейках С5 и D5 на рис. 7), постройте график за первые 18 месяцев продаж и добавьте к нему линию тренда с уравнением. Исходное значение тренда 0,8369 и исходный уровень 155,88 занесите в ячейки С5 и D5. Прогнозные данные можно представить графически (рис. 9).
Рис. 7. Экспоненциальное сглаживание Холта с корректировкой тренда; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Рис. 8. Параметры поиска решения для экспоненциального сглаживания Холта
Рис. 9. Диаграмма прогноза холтовского экспоненциального сглаживания
Выявление закономерностей в данных
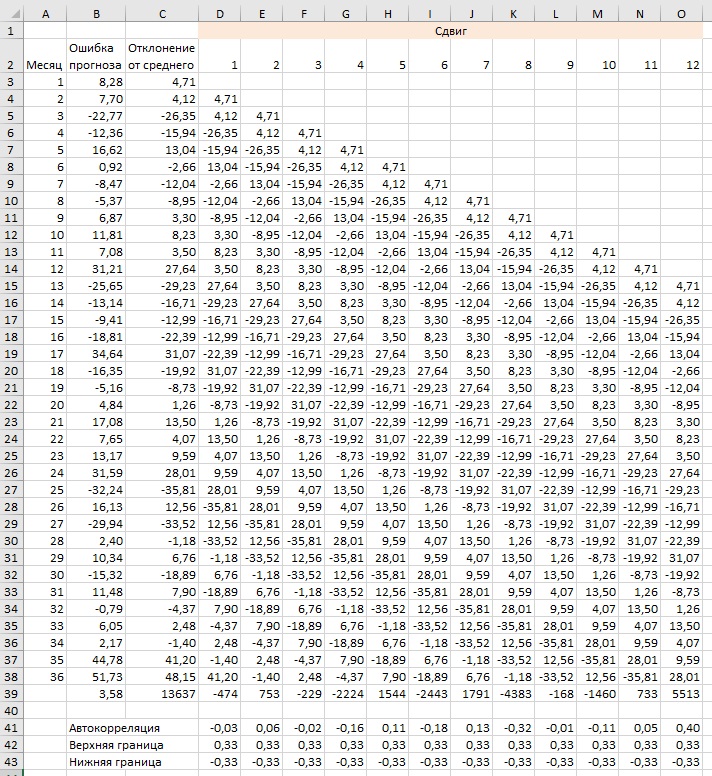
Есть способ испытать прогностическую модель на прочность — сравнить погрешности сами с собой, сдвинутыми на шаг (или несколько шагов). Если отклонения случайны, то улучшить модель нельзя. Однако, возможно, в данных о спросе есть сезонный фактор. Концепция погрешности, коррелирующей с собственной версией за другой период, называется автокорреляцией (подробнее об автокорреляции см. Простая линейная регрессия). Чтобы рассчитать автокорреляцию, начните с данных об ошибке прогноза за каждый период (столбец F на рис. 7 переносим в столбец В на рис. 10). Далее определите среднюю ошибку прогноза (рис. 10, ячейка В39; формула в ячейке: =СРЗНАЧ(B3:B38)). В столбце С рассчитайте отклонение ошибки прогноза от среднего; формула в ячейке С3: =B3-B$39. Далее последовательно сдвигайте столбец С на столбец вправо и строку вниз. Формулы в ячейках D39: =СУММПРОИЗВ($C3:$C38;D3:D38), D41: =D39/$C39, D42: =2/КОРЕНЬ(36), D43: =-2/КОРЕНЬ(36).
Рис. 10. Расчет автокорреляции
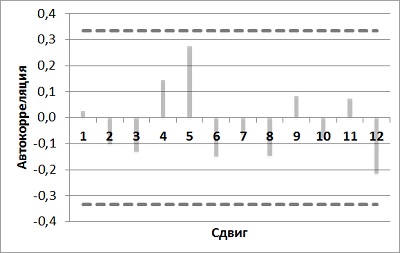
Что может значить для одного из столбцов D:O «синхронное движение» со столбцом С. Например, если столбцы С и D синхронны, то число, отрицательное в одном из них, должно быть отрицательным и в другом, положительное в одном, положительное – в другом. Это означает, что сумма произведений двух столбцов будет значительной (отличия накапливаются). Или, что тоже самое, чем ближе значение в диапазоне D41:О41 к нулю, тем ниже корреляция столбца (соответственно от D до О) со столбцом С (рис. 11).
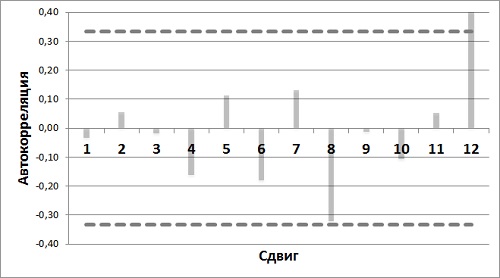
Рис. 11. Диаграмма автокорреляции
Одна автокорреляция выше критического значения. Погрешность, сдвинутая на год, коррелирует сама с собой. Это означает 12-месячный сезонный цикл. И это неудивительно. Если вы посмотрите на график спроса (рис. 2), то окажется, что есть пики спроса на каждое Рождество и провалы в апреле-мае. Рассмотрим технику прогнозирования, учитывающую сезонность.
Мультипликативное экспоненциальное сглаживание Холта-Винтерса
Метод называется мультипликативным (от multiplicate — умножать), поскольку использует умножение для учета сезонности:
Спрос в момент t = (уровень + t × тренд) × сезонная поправка для момента t × все оставшиеся нерегулярные поправки, которые мы не можем учесть
Сглаживание Холта-Винтерса также называют тройным экспоненциальным сглаживанием, потому что у него три сглаживающих параметра (альфа, гамма и сезонный фактор – дельта). Например, если имеется 12-месячный сезонный цикл:
Прогноз на месяц 39 = (уровень36 + 3 × тренд36) х сезонность27
Анализируя данные, необходимо выяснить, что в серии данных является трендом, а что — сезонностью. Чтобы выполнить вычисления по методу Холта-Винтерса, необходимо:
- Сгладить исторические данные методом скользящего среднего.
- Сравнить сглаженную версию временного ряда данных с оригиналом, чтобы получить приблизительную оценку сезонности.
- Получить новые данные без сезонного компонента.
- Найти приближения уровня и тренда на основе этих новых данных.
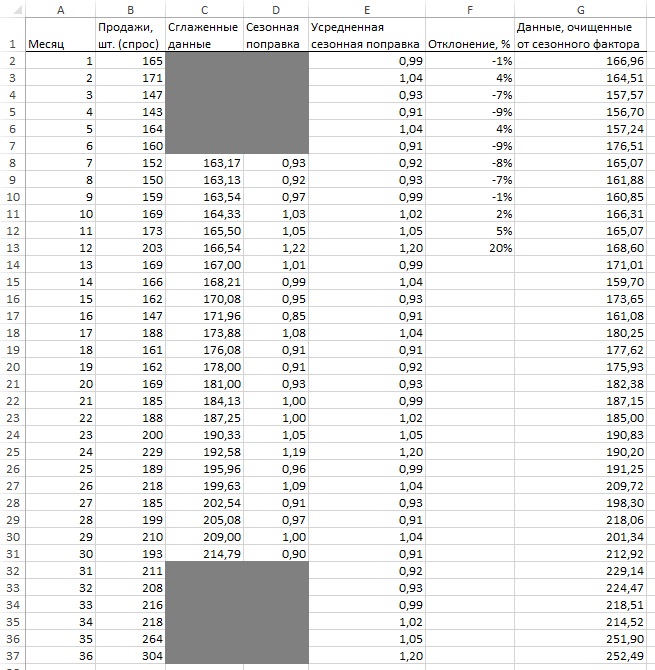
Начните с исходных данных (столбцы А и В на рис. 12) и добавьте столбец С со сглаженными значениями на основе скользящего среднего. Так как сезонность имеет 12-месячные циклы, имеет смысл использовать среднее за 12 месяцев. С этим средним есть небольшая проблема. 12 – четное число. Если вы сглаживаете спрос за месяц 7, стоит ли считать его средним спросом с 1-го по 12-й месяц или со 2-го по 13-й? Чтобы справиться с этим затруднением, нужно сгладить спрос с помощью «скользящего среднего 2×12». Т.е., взять половину от двух средних с 1 по 12-й месяц и со 2 по 13. Формула в ячейке С8: =(СРЗНАЧ(B3:B14)+СРЗНАЧ(B2:B13))/2.
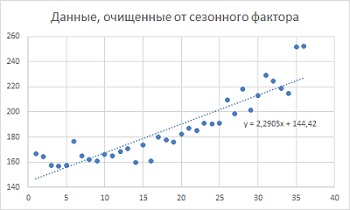
Рис. 12. Данные, очищенные от сезонного фактора
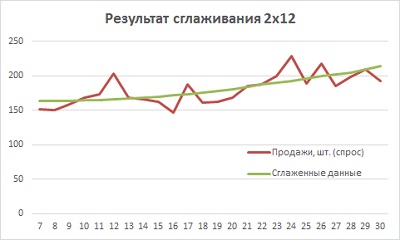
Сглаженные данных для месяцев 1–6 и 31–36 получить нельзя, так как не хватает предыдущих и последующих периодов. Для наглядности исходные и сглаженные данные можно отразить на диаграмме (рис. 13).
Рис. 13. Сглаженные данные спроса
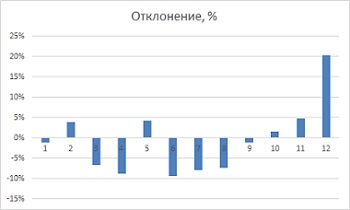
Теперь в столбце D разделите оригинальную величину на сглаженную и получите приблизительное значение сезонной поправки (столбец D на рис. 12). Формула в ячейке D8: =B8/C8. Обратите внимание на всплески в 20% выше нормального спроса в месяцах 12 и 24 (декабрь), в то время как весной наблюдаются провалы. Эта техника сглаживания дала вам две точечные оценки для каждого месяца (всего 24 месяца). В столбце Е найдено среднее значение этих двух факторов. Формула в ячейке Е1: =СРЗНАЧ(D14;D26). Для наглядности уровень сезонных колебаний можно представить графически (рис. 14).
Рис. 14. Сезонные колебания
Теперь можно получить данные, скорректированные на сезонные колебания. Формула в ячейке G1: =B2/E2. Постройте график на основе данных столбца G, дополните его линией тренда, выведите уравнение тренда на диаграмму (рис. 15), и используйте коэффициенты в последующих расчетах.
Рис. 15. Данные, скорректированные на сезонные колебания
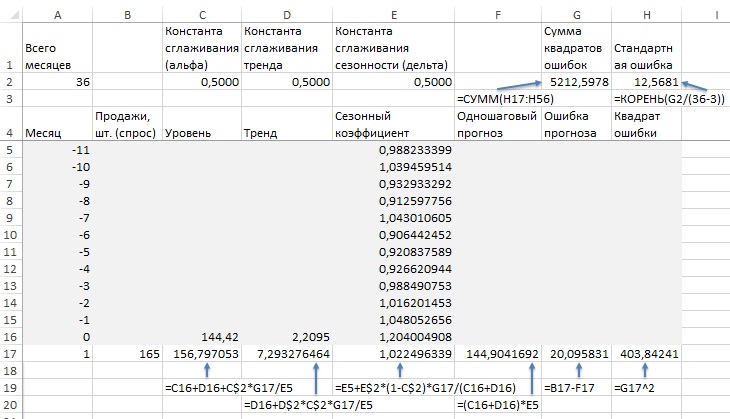
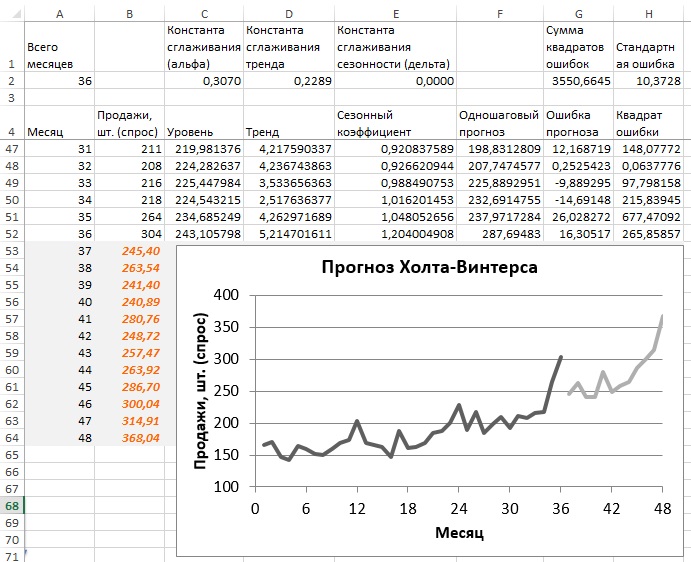
Сформируйте новый лист, как показано на рис. 16. Значения в диапазон Е5:Е16 подставьте с рис. 12 области Е2:Е13. Значения С16 и D16 возьмите из уравнения линии тренда на рис. 15. Значения констант сглаживания установите для начала на отметке 0,5. Растяните значения в строке 17 на диапазон месяцев с 1 по 36. Запустите Поиск решения для оптимизации коэффициентов сглаживания (рис. 18). Формула в ячейке В53: =(C$52+(A53-A$52)*D$52)*E41.
Рис. 16. Данные для прогноза Холта-Винтера
Рис. 17. График прогноза Холта-Винтерса
Теперь в сделанном прогнозе нужно проверить автокорреляции (рис. 18). Так как все значения расположились между верхней и нижней границами, вы понимаете, что модель неплохо поработала над пониманием структуры значений спроса.
Рис. 18. Коррелограмма модели Холта-Винтерса
Построение доверительного интервала прогноза
Итак, у нас есть вполне рабочий прогноз. Как установить верхние и нижние границы, которые можно использовать для построения реалистичных предположений? В этом вам поможет симуляция Монте-Карло, с которой вы уже встречались в главе 4 (см. также Использование метода Монте-Карло для расчета риска). Смысл заключается в том, чтобы сгенерировать будущие сценарии поведения спроса и определить группу, в которую попадают 95% из них.
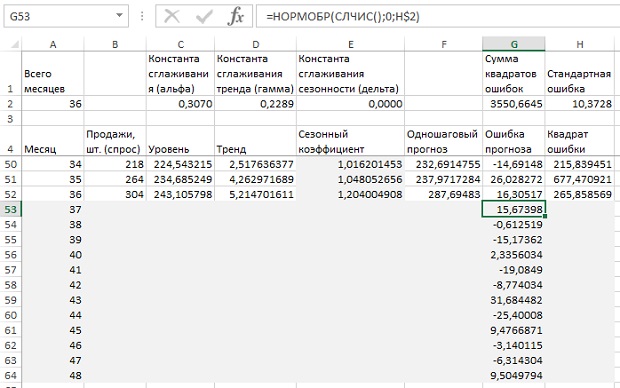
Удалите с листа Excel прогноз из ячеек В53:В64 (см. рис. 17). Вы запишете туда спрос на основе симуляции. Последнюю можно сгенерировать с помощью функции НОРМОБР. Для будущих месяцев вам достаточно снабдить ее средним (0), стандартным распределением (10,37 из ячейки $Н$2) и случайным числом от 0 до 1. Функция вернет отклонение с вероятностью, соответствующей колоколообразной кривой. Поместите симуляцию одношаговой погрешности в ячейку G53: =НОРМОБР(СЛЧИС();0;H$2). Растянув эту формулу вниз до G64, и вы получите симуляции ошибки прогноза для 12 месяцев одношагового прогноза (рис. 19). Ваши значения симуляций будут отличаться от приведенных на рисунке (на то она и симуляция!).
Рис. 19. Симулированные ошибки прогноза
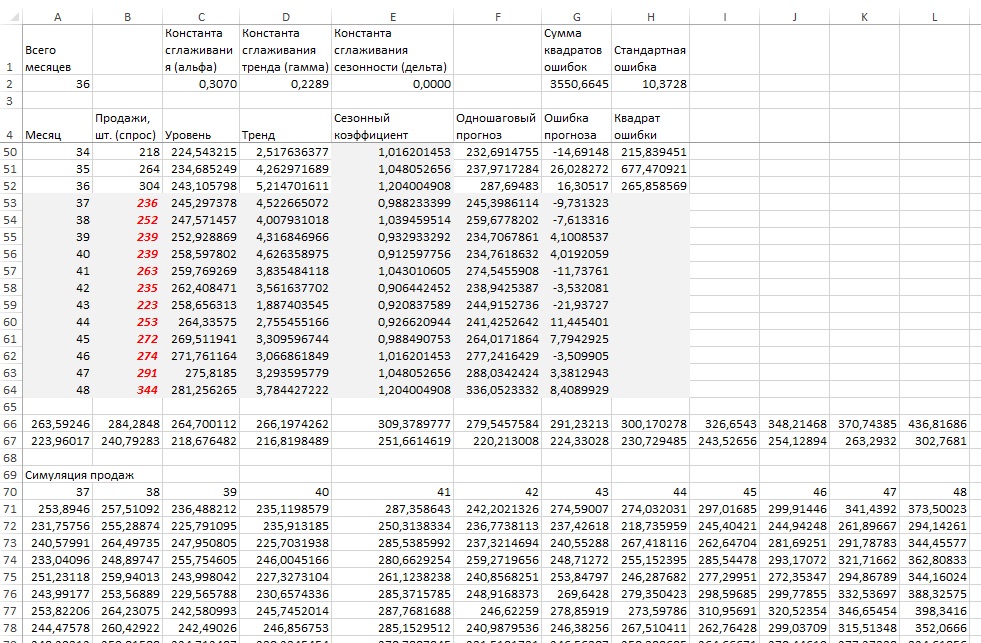
С погрешностью прогноза у вас есть все, что нужно для обновления уровня, тренда и сезонного коэффициента. Так что выделите ячейки C52:F52 и растяните их до строки 64. В результате у вас имеются симулированная ошибка прогноза и сам прогноз. Идя от обратного, можно спрогнозировать значения спроса. Вставьте в ячейку В53 формулу: =F53+G53 и растяните ее до В64 (рис. 20, диапазон В53:F64). Теперь вы можете нажимать на кнопку F9, каждый раз обновляя прогноз. Разместите результаты 1000 симуляций в ячейках А71:L1070, каждый раз транспонируя значения из диапазона В53:В64 в диапазон А71:L71, A72:L72, … A1070:L1070. Если вас это напрягает напишите код VBA.
Рис. 20. Тысяча сценариев дают хорошую оценку 95%-ного доверительного интервала
Теперь у вас есть по 1000 сценариев на каждый месяц, и вы можете использовать функцию ПЕРСЕНТИЛЬ, чтобы получить верхние и нижние границы в середине 95%-ного доверительно интервала. В ячейке А66 формула: =ПЕРСЕНТИЛЬ(A71:A1070;0,975), а в ячейке А67: =ПЕРСЕНТИЛЬ(A71:A1070;0,025).
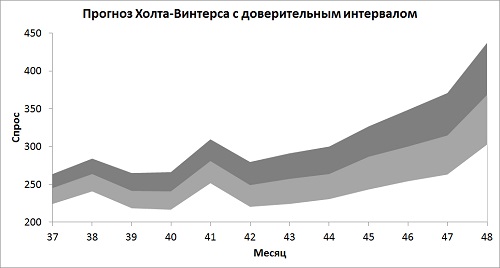
Как обычно, для наглядности данные можно представить в графическом виде (рис. 21).
Рис. 21. Прогностический интервал по Холту-Винтерсу
На графике есть два интересных момента:
- Погрешность со временем становится шире. В этом есть смысл. Неуверенность накапливается с каждым месяцем.
- Точно так же погрешность растет и в частях, приходящихся на периоды сезонного повышения спроса. С последующим его падением погрешность сжимается.
[1] Написано по материалам книги Джона Формана Много цифр: Анализ больших данных при помощи Excel. – М.: Альпина Паблишер, 2016. – С. 329–381


Спасибо большое! отличная статья
Здравствуйте.
На каком основании взято, что кртическое значение для проверки значений автокорреляции вычисляется по формуле 2/КОРЕНЬ(36)?
Автор книги (Джон Форман) просто написал: «Обычно критические значения проводят на уровне ± 2/корень из количества точек данных». Рекомендую также посмотреть раздел «Статистика Дурбина-Уотсона» заметки
Простая линейная регрессия.Очень путаный пример мультипликативного экспоненциального сглаживания Холта-Винтерса получился, сложно проследить алгоритм и спроецировать на свои данные. После построения линии тренда для сезонных колебаний можно ли действия в экселе подробно описать?
Игорь, рекомендую обратиться к первоисточнику — книге Формана. Там расписано еще подробнее…
Добрый день!
Подскажите, а почему мы (в примере про ПЭС) с 37 периода берем постоянное значение, а не протягиваем дальше столбец С? Ведь мы уже на имеющихся данных выбрали подходящую альфа, минимизирующую ошибки — значит, есть уже модель прогнозная, можно по аналогии построить до конца. А так получается прогноз только на один период (37й).
Понятно, что там нулевой прогноз ошибки, но все равно…Может, можно было бы построить тренд по данным из столбца С? Просто как-то странно, все будущие прогнозные периоды одинаковые.
Екатерина, здравствуйте. Т.к это модель простого экспоненциального сглаживания, далее можно использовать более усложненные модели с трендом, сезонностью, мультипликативной или адаптивной ошибкой и экзогенными переменными. Если вам интересно я сейчас в Excel реализую эти модели, могу поделиться файлом.
Да, было бы интересно. Но у вас есть сайт, где можно посмотреть? Принимать файл со стороны небезопасно(
К сожалению сайта нет.
Андрей,а можете прислать ссылку с гугл диска на ваш файл?
Сылка на файл ниже
https://drive.google.com/open?id=1G3SBgHUGJxuEj4vozw49fzcrFXJGWOd7
Подскажите, а чем отличается ПЭС от экспоненциального сглаживания, которое Вы описываете в другой заметке — анализ временных рядов
На мой взгляд, они немного различаются. Когда имеет смысл какой из этих двух методов применять?
Екатерина, здравствуйте.
Выбор модели прогнозирования определяется исходя из оценок прогноза каждой конкретной модели, классических оценок около 10 (IC, MAPE, MASE, MAE и т.д).
На данный момент разновидностей моделей экспоненциального сглаживания разработано достаточно много, классических моделей только 30 шт. По данному вопросу необходимо изучить книгу: Forecasting with Exponential Smoothing The State Space Approach Rob J. Hyndman, Anne B. Koehler,
J. Keith Ord and Ralph D. Snyder.