Герой Бена Аффлека в фильме Расплата выполняет аудит компании по производству робототехники. Сотрудница финансового отдела компании обнаружила несоответствие на миллионы долларов. Аффлек анализирует первые цифры счетов, и обнаруживает их неестественность. Злой умысел подтвержден…

Бен Аффлек и Анна Кендрик в фильме Расплата
Предыдущая глава Оглавление Следующая глава
Скачать заметку в формате Word или pdf
Закон Бенфорда
Он известен еще, как закон первой цифры, и гласит, что в числах, основанных на данных из жизни, цифра 1 на первом месте встречается гораздо чаще, чем все остальные.
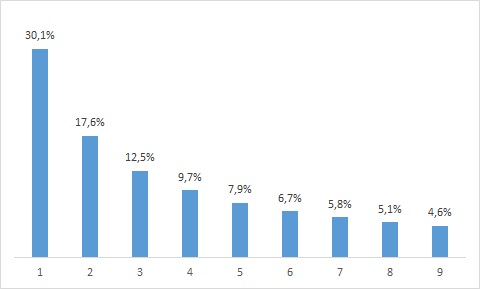
Закон Бенфорда (см. в Excel): по горизонтали – первые значащие цифры данных, по вертикали – вероятность их появления
Американский астроном Саймон Ньюком в 1881 г. заметил, что страницы логарифмических таблиц, на которых числа начинались с единицы, истрепаны гораздо сильнее. Он предположил, что такие числа встречались в расчетах чаще, и вывел эмпирическую закономерность. В 1938 г. Фрэнк Бенфорд переоткрыл эту закономерность. Она применима ко множествам чисел, которые могут расти экспоненциально. В их число входят суммы счетов, цены на акции, численность населения стран, длины рек, площади водоемов… Закон как нельзя лучше подходит для обработки большого массива финансовых показателей на предмет мошенничества.
Закон Ципфа
В середине XX в. социолог Джордж Кингсли Ципф вывел эмпирическую закономерность распределения частот слов естественного языка. Если слова любого текста ранжировать по частоте использования, то произведение ранга на частоту есть величина постоянная:
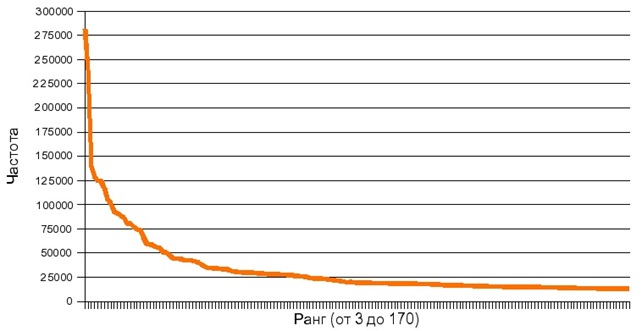
F*R =C, где:
F – частота появления слова в тексте;
R – ранг слова (наиболее употребляемое слово получает ранг 1, следующее – 2 и т.д.);
С – константа; Ципф экспериментально определил, что С ≈ 0,1.
Закон Ципфа: график для частот слов из статей русской Википедии
Принцип Парето
Ципф рассматривал степенные законы как вездесущие структуры общественных наук. Степенные законы также широко представлены в физике. Например, шкала Рихтера для измерения силы землетрясений. Слабые землетрясения обычны, тогда как сильные редки, а частота и сила землетрясений связаны формулой на основе степенной зависимости. В то же время закон Ципфа является не чем иным, как принципом Парето «наоборот».
В самом общем виде принцип Парето заключается в следующем: основные результаты достигаются небольшим числом усилий. При этом часто (но не обязательно) наблюдается пропорция 80/20. Например, 20% клиентов дают 80% продаж; 80% товарного запаса приходится на 20% номенклатуры; 80% брака является следствием 20% всех возможных причин… Философия принципа Парето – сущности распределяются неравномерно, и дают не одинаковый вклад в итоговый результат.
Фракталы и финансовые рынки
Случайности различной природы…
- игровой (рулетка, бросание костей),
- технологической (диаметр вала, изготавливаемого на токарном станке)
- физической (рост взрослого человека)
… описываются кривой Гаусса. Но целый ряд явлений не подчиняются этому распределению: богатство стран и отдельных людей, колебания цен на акции, курсы валют, частота использования слов, сила землетрясений… Для таких явлений характерным является то, что среднее значение сильно зависит от выборки.
Бенуа Мандельброт, изучая степенные ряды показал, что они приводят к фрактальной природе экономических и социальных систем. Хвосты распределения не уменьшаются до бесконечности, а остаются толстыми довольно далеко от средних значений.
Фрактал – геометрический объект, обладающий свойством самоподобия. Вид фрактала не зависит от масштаба. Все диаграммы выглядят одинаково: в отсутствие условных обозначений никто не скажет, какой именно период времени – минуты, часы или годы – охватывает ценовая диаграмма:
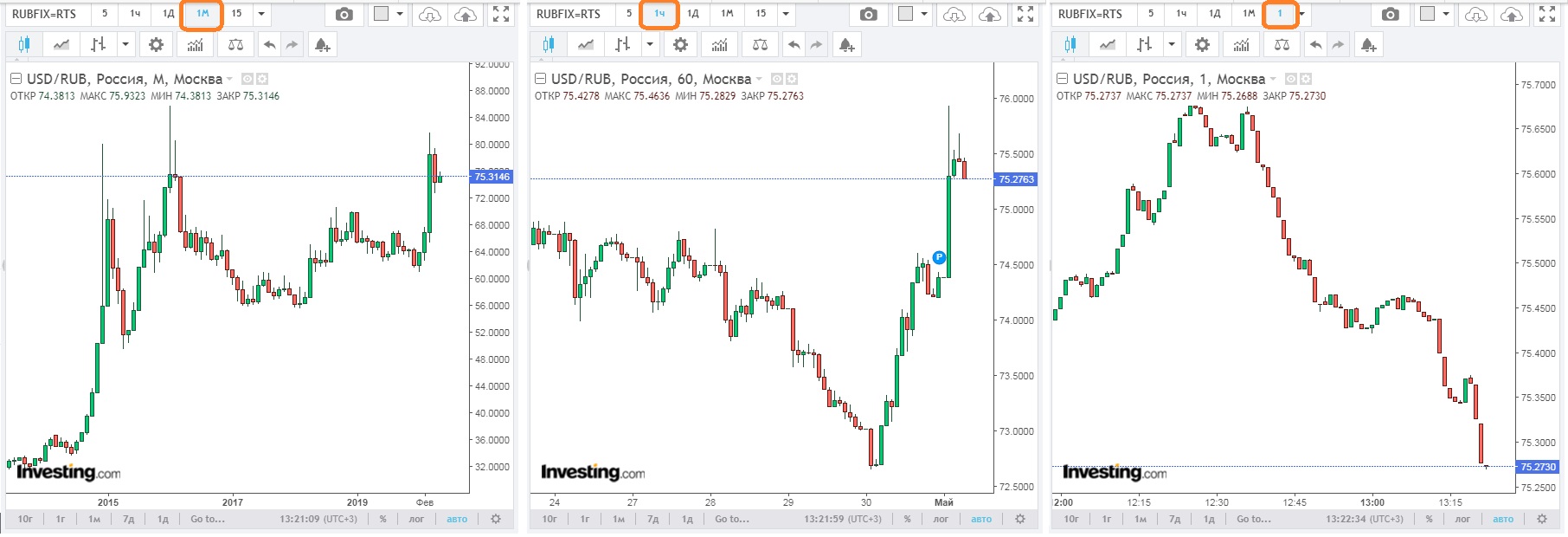
Курс рубля к доллару на трех временных горизонтах: месяц, час, минута; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Благодаря тому, что всего два числа – среднее значение и стандартное отклонение – говорят нам все необходимое о генеральной совокупности, кривая Гаусса приобрела столь широкую популярность. Мир финансов совершенно иной. В нем ошибки распределены не так, как почти одинаковые песчинки; они представляют собой смесь песчинок, гравия, валунов и гор. Финансовые рынки управляются фрактальной статистикой на основе долговременной памяти. Движение цен описывается не колоколообразной кривой, а степенными рядами, значительно более бурными. Рынки вводят в заблуждение. Графики цен легко одурачат любого профессионала, который отыщет в них закономерности просто из-за присущей человеческой натуре потребности находить закономерности там, где их нет.
Литература
Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью. М.: Livebook/Гаятри, 2010. – 352 с. Конспект: https://baguzin.ru/wp/?p=4219
Закон Бенфорда или закон первой цифры: https://baguzin.ru/wp/?p=4367
Закон Ципфа и фрактальная природа социальных и экономических явлений: https://baguzin.ru/wp/?p=1716
АВС-анализ и принцип Парето для бизнеса: https://baguzin.ru/wp/?p=310
Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах. – М.: Издательский дом Вильямс, 2006. – 400 с. Конспект: https://baguzin.ru/wp/?p=1604