Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения – чем стандартное отклонение отличается от стандартной ошибки, и в каких случаях, применять ту или иную статистику. А недавно в книге Искусство статистики Дэвида Шпигельхалтера я узнал про бутстрэппинг, и понял, как объяснить различия стандартного отклонения и стандартной ошибки.
Для начала зададим 100 значений стандартной нормально распределенной случайной величины. В этом контексте стандартная означает, что ее матожидание μ = 0, а среднеквадратичное отклонение σ = 1. Поскольку значения в Excel получены с помощью волатильной функции СЛМАССИВ(), после любого действия они пересчитываются. Поэтому диаграммы в заметке и в файле будут отличаться.
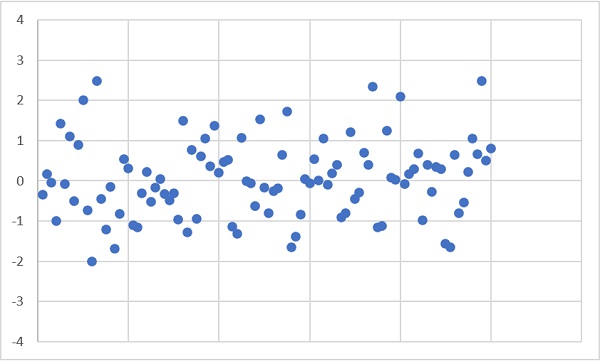
Рис. 1. Нормально распределенная случайная величина
Скачать заметку в формате Word или pdf, примеры в формате Excel
Стандартное отклонение
… является наиболее распространенным показателем рассеивания значений случайной величины относительно её среднего арифметического.
Стандартное отклонение вычисляют по формуле:
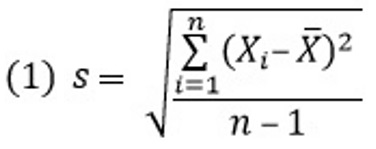
где X̅ – среднее арифметическое значений случайной величины (далее я буду называть его просто средним), Хi – отдельные значения случайной величины, n – число значений случайной величины.
Вообще термины разными авторами используются немного по-разному. Мне нравится следующий подход. Генеральную совокупность описывают параметрами, обозначаемыми греческими буквами: математическое ожидание μ и среднеквадратичное отклонение σ. Выборки описывают статистиками, обозначаемыми латинскими буквами: среднее арифметическое X̅ и стандартное отклонение s. Стандартное отклонение иначе называют оценкой среднеквадратичного отклонения. Как правило, есть генеральная совокупность с неизвестным нам среднеквадратичным отклонением σ. Извлекая выборку, и вычисляя стандартное отклонение s, мы кое-что узнаем о среднеквадратичном отклонении генеральной совокупности σ. Поэтому и говорят, что s является оценкой сигмы.
На самом деле за термином стандартное отклонение стоят две немного отличающиеся статистики. Но эта заметка о другом)) Подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?
Нанесем на диаграмму линию среднего и границы, отстоящие от среднего на расстоянии ±2s.

Рис. 2. Линия среднего и границы ±2s
Для стандартного нормального распределения за границы ±2s попадают 4,6% значений.
=(1-НОРМ.СТ.РАСП(2;ИСТИНА))*2 = 4,6%
И действительно 5 точек на рис. 2 лежат вне границ. Совпадение не обязано быть таким точным. Если вы откроете файл Excel на листе «Рис. 2» и понажимаете F9, принудительно изменяя случайные значения, то увидите, что вне границ может лежать от 2 до 8 точек. А если нажимать F9 достаточно долго, то вы получите более экстремальные числа точек вне границ. Для стандартного нормального распределения в пределах ±2s лежат приблизительно 95% значений. Поскольку s – оценка среднеквадратичного отклонения σ, которое в свою очередь равно 1, то 95% всех значений попадают в диапазон ≈ ±2.
Чем меньше s, тем кучнее значения случайной величины располагаются вокруг среднего. Итак
стандартное отклонение – мера разброса случайной величины
Среднее арифметическое выборки
Напомню, что мы задаем наши 100 значений с помощью генератора случайных чисел формулой в Excel
=НОРМ.СТ.ОБР(СЛМАССИВ(100;;0;1;ЛОЖЬ))
Хотя мы установили для генератора случайных чисел μ = 0 и σ = 1, значения X̅ и s будут немного отличаться для каждой выборки.
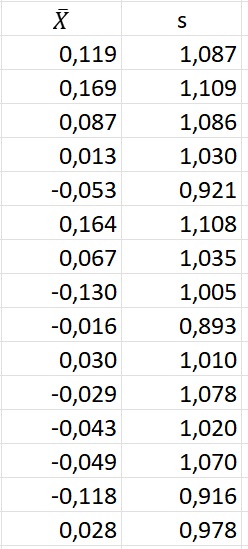
Рис. 3. Среднее и стандартное отклонение для 15 выборок размером n = 100
Теперь мы хотим узнать, что можно сказать о неизвестном математическом ожидании генеральной совокупности μ, подсчитав среднее арифметическое конкретной выборки, например, первой X̅ = 0,119?
Бутстрэп
Как пишет Евгения Поникарова, переводчик книги Дэвида Шпигельхалтера «Искусство статистики», слово bootstraps означает ремешки в виде ушка, которые прикрепляются к верхней части обуви, чтобы ее было проще натягивать. В английском языке есть выражение To pull oneself over a fence by one’s bootstraps (буквально — перетащить себя через ограду за ушки своей обуви), которое означает «выпутаться из своих проблем самому». Еще можно вспомнить барона Мюнхгаузена, который вытащил себя за волосы из болота.
Бутстрэп – компьютерный метод исследования распределения статистик, основанный на многократной генерации выборок методом Монте-Карло на базе имеющейся одной выборки. Термин ввел в 1977 году Брэдли Эфрон.
Итак, возьмем одну выборку из 100 случайных чисел и зафиксируем значения. Это наша исходная выборка (столбец А на рис. 4). Её среднее X̅(100) = 0,121, а стандартное отклонение s(100) = 0,995. 95% значений попадают в диапазон ≈ 0,121 ± 1,990.
С помощью генератора случайных чисел будем формировать из исходной выборки бутстрэп-выборки разного размера. Хитрость заключается в том, что выбирать значения мы будем с возвращением. Т.е., все значения любой бутстрэп-выборки взяты из исходной, а вот уникальность значений будет потеряна. Например, выборка в столбце С содержит два значения 0,7394. Я подсветил их с помощью условного форматирования. Опять же, если вы откроете Excel-файл, то дублей может не быть, так как бутстрэп-выборка сформирована волатильной функцией СЛМАССИВ().
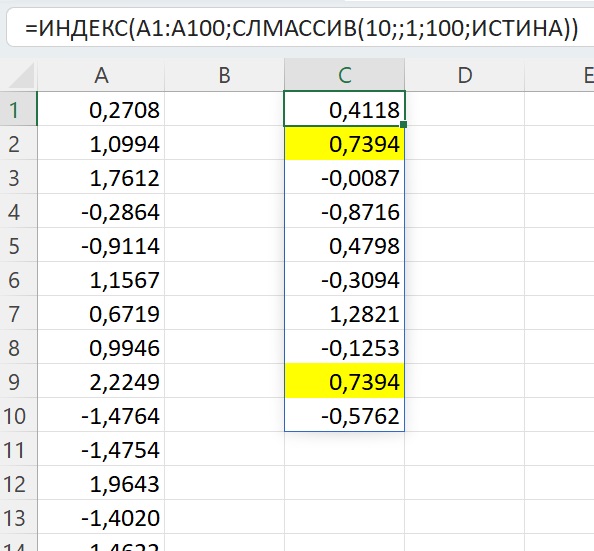
Рис. 4. Бутстрэп-выборка может содержать повторения
Для удобства последующей обработки расположим значения бутстрэп-выборки по горизонтали. Начнем со значения n = 3. Извлечем 1000 бутстрэп-выборок (рис. 5). В столбце А исходная выборка, n = 100. Столбец С содержит номер бутстрэп-выборки. В столбцах D, E и F извлеченные значения, в G – средние значения по выборкам. В ячейке G1 среднее D1:F1, в ячейке G2 – среднее D2:F2 и т.д. На диаграмме показано распределение средних значений бутстрэп-выборок для n = 3.
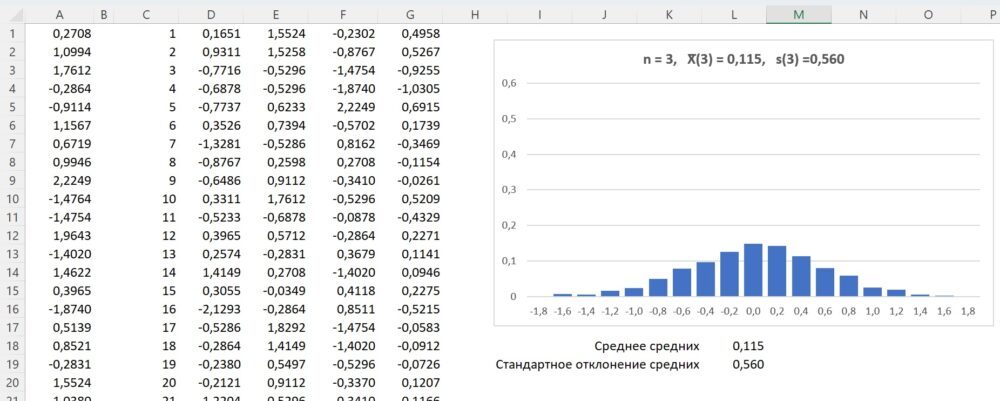
Рис. 5. Распределений средних значений 1000 бутстрэп-выборок, n = 3
Среднее средних 1000 бутстрэп-выборок = 0,115, стандартное отклонение средних значений 1000 бутстрэп-выборок = 0,560. Напоминаю, что 95% исходных значений выборки попадают в диапазон 0,12 ± 1,99. Для бутстрэп-выборок n = 3 мы только что нашли, что 95% средних попадают в диапазон 0,115 ± 1,120 (0,560*2 = 1,120). Кажется естественным, что разброс средних меньше, чем разброс отдельных значений.
Повторим моделирование для n = 5, 20, 50.
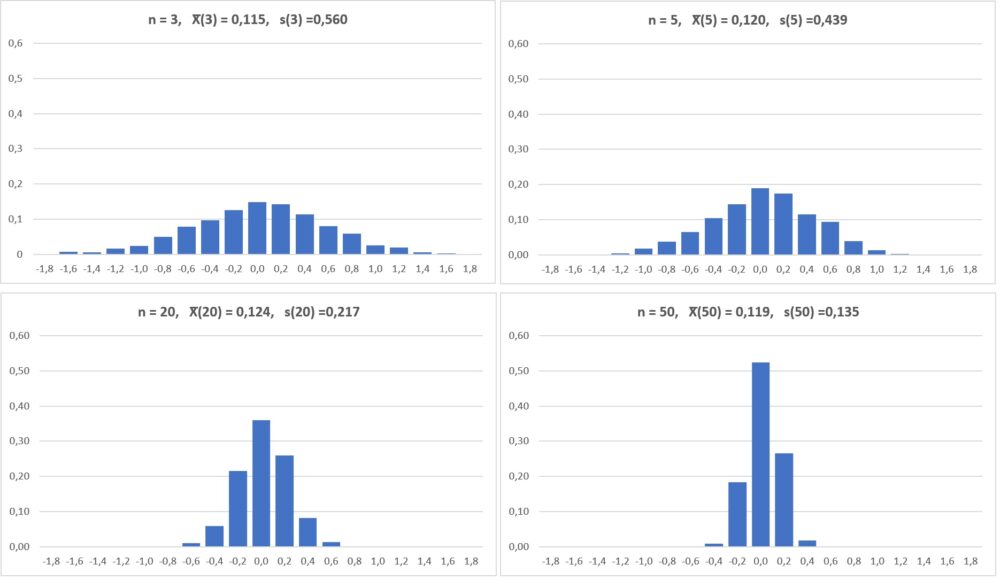
Рис. 6. С увеличением n стандартное отклонение средних значений бутстрэп-выборок уменьшается
Осмыслим, что мы получили. На рис. 6 представлены распределения средних значений бутстрэп-выборок разного размера из исходной выборки 100 случайных нормально распределенных чисел. Среднее каждого распределения близко к нулю (в нашей конкретной выборке из 100 чисел это среднее равно 0,121). А вот стандартное отклонение s(n) уменьшается по мере роста размера бутстрэп-выборок: s(3) = 0,560, s(5) = 0,439, s(20) = 0,217, s(50) = 0,135.
Стандартна ошибка
…или стандартная ошибка среднего – статистика, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности.
Ничего не напоминает!? А что за статистику s(n) мы рассчитали выше в бутстрэп-анализе!? Да, это было стандартное отклонение выборочного среднего X̅(n).
Величина стандартной ошибки зависит от дисперсии генеральной совокупности σ2 и объёма выборки n. Стандартная ошибка среднего вычисляется по формуле
![]()
где σ – величина среднеквадратического отклонения генеральной совокупности, и n – объём выборки. Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле:
![]()
где s — стандартное отклонение случайной величины.
Сведем в одной таблице рассмотренные статистики:

Рис. 7. Рассмотренные статистики
Здесь в столбцах J:L приведены статистики для одной выборки размера n, а в столбце M – статистики для бутстрэп-выборок соответствующего размера с рис. 6. Если в Excel-файле на листе «Рис. 7» понажимать F9, вы увидите, что не всегда совпадение между столбцами L и M будет таким хорошим, но тенденция будет прослеживаться.
Выше я писал, что мы исследуем неизвестное математическое ожидание генеральной совокупности μ на основе среднего арифметического выборки X̅(100) = 0,119.
Мы можем использовать статистику, именуемую стандартной ошибкой. Для нас она черный ящик – формула, выведенная на основе теории вероятностей. С другой стороны мы можем построить множество бутстрэп-выборок размера n = 100, и подсчитать стандартное отклонение средних этих бутстрэп-выборок. И мы показали, что стандартная ошибка для одной выборки и стандартное отклонение средних бутстрэп-выборок, это одно и то же! В нашем примере, получив X̅(100) = 0,119, мы можем сказать, что с вероятностью 95% математическое ожидание генеральной совокупности μ лежит в диапазоне 0,119 ± 0,212 (0,106*2=0,212). Итак
стандартная ошибка – мера оценки математического ожидания генеральной совокупности μ на основании статистик выборки
Например, 95%-ный доверительный интервал для μ
Понятно, что с увеличением размера выборки n доверительный интервал будет сужаться. В пределе при n → ∞, X̅ → μ и SE → 0.