Эта заметка родилась на стыке трех моих увлечений: футбол, Excel и статистика)) Известно, что число голов, забитых каждой командой в одном матче подчиняется распределению Пуассона. Я решил проверить это на результатах матчей английской премьер-лиги сезона 2021/2022. Всего было 38 туров по 10 матчей в туре, по две команды в одном матче. Итого 760 исходных значений.
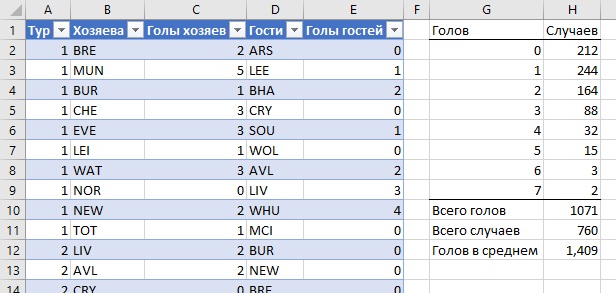
Рис. 1. Распределение числа забитых голов
Скачать заметку в формате Word или pdf, примеры в формате Excel
Распределение Пуассона
Распределение Пуассона имеет один параметр λ – среднее количество успешных испытаний в заданной области возможных исходов. Количество успешных испытаний Х пуассоновской случайной величины изменяется от 0 до бесконечности. Плотность распределения Пуассона описывается формулой:
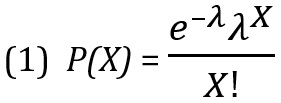
где Р(Х) – вероятность ровно X успешных испытаний, λ – среднее ожидаемое количество успехов, е – основание натурального логарифма, равное 2,71828, X – количество успехов.
В Excel плотность распределения Пуассона можно задать формулой =ПУАССОН.РАСП(Х; λ; ЛОЖЬ). Чтобы сравнивать одинаковые сущности, я разделил число случаев (столбец Н на рис. 1) на общее число случаев. И получил вероятности (столбец В на рис. 2). Также я подсчитал плотность распределения Пуассона для Х = 0, 1, …, 7 при λ = 1,409 (столбец С на рис. 2). Например, вероятность не забить ни одного гола Х = 0 задается формулой =ПУАССОН.РАСП(0;1,409;ЛОЖЬ) = 0,244 или 24,4%.
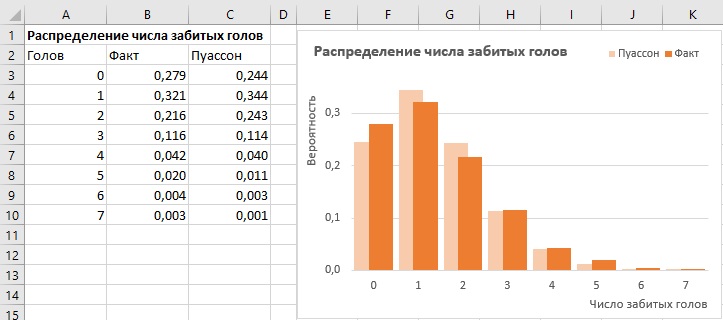
Рис. 2. Вероятности забить n голов в сезоне 2021/22 и распределение Пуассона для λ = 1,409
Статистический вывод
Глядя на рис. 2 можно заметить, что фактические вероятности забить n голов и вероятности, соответствующие распределению Пуассона для среднего λ = 1,409 неплохо совпадают. Статистический вывод позволяет количественно оценить, насколько «неплохо».
Итак, в качестве нулевой гипотезы Н0 примем, что наша выборка по результатам сезона 2021/22 происходит из генеральной совокупности, подчиняющейся распределению Пуассона с λ = 1,409. В качестве альтернативной гипотезы Н1 будем считать, что выборка происходит из генеральной совокупности, описываемой иным распределением.
Осталось выбрать статистику, которая позволит сравнить с одной стороны расхождения между фактическим и распределением Пуассона, а с другой – с критическим значением статистики, соответствующим α = 5% или, что еще строже, α = 1%. t-статистика не подходит, и я решил впервые в своей практике воспользоваться статистикой Колмогорова.
Статистика Колмогорова
Критерий согласия Колмогорова служит для проверки гипотезы о принадлежности значений выборки определённому теоретическому закону распределения. В нашем случае мы хотим проверить принадлежит ли фактическое распределение частоты голов в сезоне 2021/22 распределению Пуассона.
Статистика критерия задается формулой
![]()
где Fn(x) – эмпирическая интегральная функция на участке от 0 до х; F(x, Θ) – теоретическая интегральная функция с параметром Θ на участке от 0 до х; х – значения, для которых получено эмпирическое распределение, в нашем случае – число голов от 0 до 7; n – объем выборки, в нашем случае – 760; sup – супремум, почти синоним максимума. В нашем примере теоретическая функция с параметром Θ – это распределение Пуассона с неизвестным параметром λ. Мы заменяем неизвестный параметр λ, значением 1,409, полученным из экспериментальных данных (см. дополнение от 10.12.2022 ниже).
Изобразим наши данные в терминах уравнения (2):
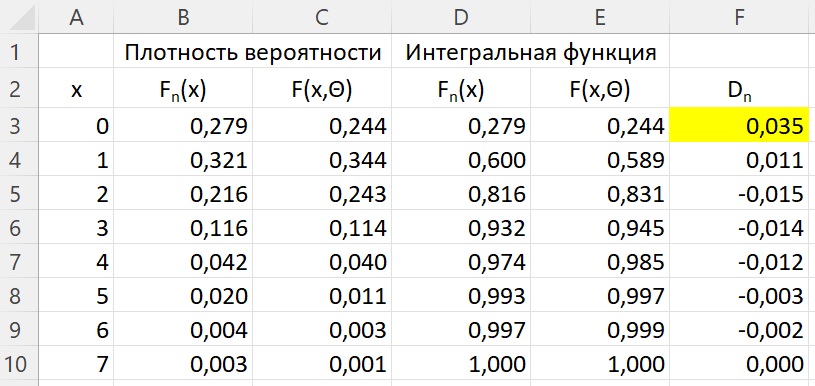
Рис. 3. Разница Dn интегральных функций распределения: фактической и Пуассона
Здесь в столбцах D и E я отразил интегральные (накопленные) частоты, как сумму частот для отдельных значений из столбцов В и С. В столбце F подсчитана разность значений соответствующих строк столбцов D и E. Видно, что максимальная разница между интегральными функциями фактического и распределения Пуассона достигается в первой точке при х = 0.
Распределение Колмогорова
Распределение Колмогорова имеет вид (k – целое):
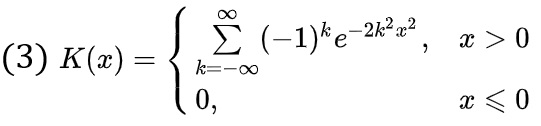
Современный Excel позволяет построить распределение Колмогорова на основании формулы (3) без обращения к таблицам из справочников (см. Excel-файл лист «Рис. 4»)
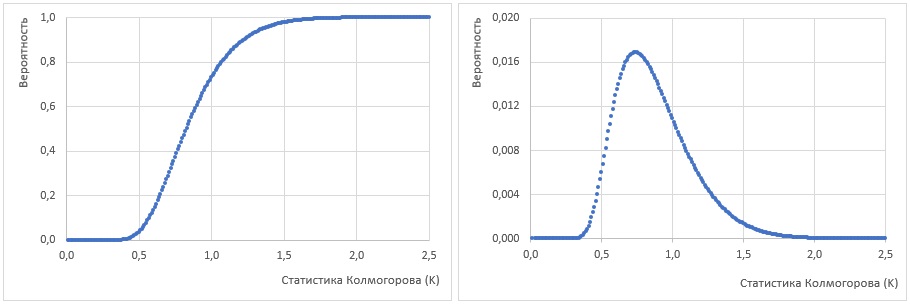
Рис. 4. Функция распределения Колмогорова: а) интегральная; б) плотность вероятности
Кривая плотности вероятности распределения Колмогорова подобна нормальной, но с ярко выраженным правым хвостом.
Статистика Колмогорова является правосторонней, и в соответствии с теоремой Колмогорова…
![]()
… позволяет находить доверительные интервалы теоретической функции распределения F(x,Θ).
Критерий Колмогорова
Следуя традиции, можно использовать два доверительных интервала для отклонения нулевой гипотезы Н0: 95%-ный и 99%-ный:
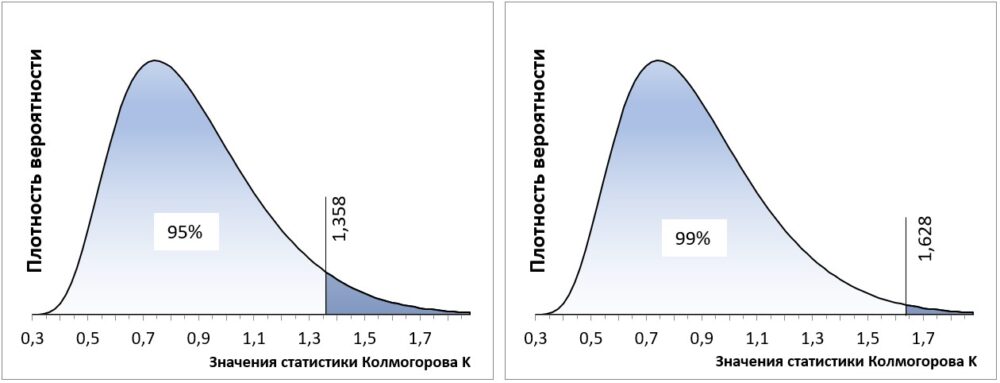
Рис. 5. Области отклонения нулевой гипотезы (более темные), и соответствующие им значения статистики Колмогорова (K)
Таким образом, для отклонения нулевой гипотезы с достоверностью 95% необходимо, чтобы эмпирическое значение статистики Колмогорова (K) превысило K95% = 1,358. Для отклонения нулевой гипотезы с достоверностью 99% необходимо, чтобы эмпирическое значение статистики Колмогорова (K) превысило K99% = 1,628.
Проверка соответствия частоты голов распределению Пуассона
Теперь осталось сравнить Dn = 0,035 (см. рис. 3) со значениями критерия Колмогорова для n = 760 при уровне значимости α = 0,05 и α = 0,01. Для этого надо перейти от Dn к K, используя формулу (4).
![]()
Результат сравнения удобно изобразить на числовой прямой:

Рис. 6. Зоны отклонения нулевой гипотезы
Нулевую гипотезу о соответствии распределения частот голов в сезоне 2021/22 распределению Пуассона с λ = 1,409 на основании критерия Колмогорова отклонить нельзя. Т.е., частота голов в английской премьер-лиге сезона 2021/22 подчиняется распределению Пуассона.
Дополнение от 10.12.2022. Дмитрий в комментариях обратил мое внимание, что использование распределения Колмогорова для статистического вывода о Kэксп. = 0,954 не корректно. Т.е., сравнение Kэксп. = 0,954 нужно вести не с K95% = 1,358 и K99% = 1,628, а с другими значениями, полученными не на основании распределения Колмогорова (3), а на основании иного распределения.
В нашем примере теоретическая функция с параметром Θ – это распределение Пуассона с неизвестным параметром λ. Если бы мы знали параметр λ, то могли бы сравнить статистику критерия Колмогорова (2) с распределением Колмогорова (3). Что я и сделал в заметке. Мы же знаем только оценку параметра λ, подсчитанную по выборке за сезон 2021/22 и равную 1,409. Когда по анализируемой выборке оцениваются параметры теоретического закона, согласие с которым проверяется, статистика критерия Колмогорова может существенно отличаться от распределения Колмогорова. Как считает Александр Иванович Орлов если пренебрегать этим отличием, согласие с проверяемым законом будет подтверждаться чаще, чем следует. Математический аппарат, который используется в этом случае, выходит за рамки уровня моего блога))
При беглом знакомстве с работами А.И. Орлова я нашел лишь критику использования распределения Колмогорова, когда по анализируемой выборке оцениваются параметры теоретического закона, согласие с которым проверяется. Позитивную программу, что делать в этом случае, я нашел в работах Бориса Юрьевича Лемешко, к которым отсылаю заинтересованных читателей.
Добрый день.
А как Вы определили значение лямбда для проверки? Взяли среднее по выборке?
Да. Я пишу «В нашем примере теоретическая функция с параметром Θ – это распределение Пуассона с неизвестным параметром λ. Мы заменяем неизвестный параметр λ, значением 1,409, полученным из экспериментальных данных. Это ослабляет мощь критерия Колмогорова, но его всё еще можно использовать.»
Посмотрите статьи или учебники профессора А.И. Орлова. В Вашем случае, когда параметры генеральной совокупности неизвестны и определяются по выборке, то это критерий типа Колмогорова-Смирнова. У него распределения и критические значения другие и уже зависит на соответствие какому распределению проверяется выборка.
Дмитрий, спасибо. Согласен с вашим замечанием. Опубликовал дополнение.