Говоря о вероятностях важно различать априорную, эмпирическую и субъективную вероятности. В первом случае вероятность события оценивается на основе теоретической (априорной) частоты. Например, вероятность появления шестерки при бросании кости равна ⅙. Эмпирическая вероятность изучается на опыте. Например, контрольная карта Шухарта позволяет оценить вероятность того, что параметр процесса будет находиться внутри контрольных границ. Субъективная вероятность представляет собой шанс, который приписывается событию человеком. Другой человек может иначе оценивать шансы того же события.
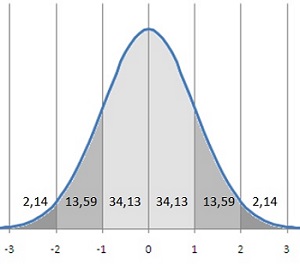
Нормальное распределение: по оси абсцисс – число стандартных отклонений; десятичные числа на диаграмме – вероятность в процентах попадания случайной величины в диапазон
Предыдущая глава Оглавление Следующая глава
Скачать заметку в формате Word или pdf
Нормальное распределение
Многое в мире подвержено вариациям. Например, рост человека, интернет-трафик или доходы на семью. Всё это примеры случайной величины. По определению, – это такая величина, которая в результате измерения может принять некое значение, причем какое именно заранее неизвестно. Случайные величины измеряются в различных единицах (см, МБ, руб.), но путем преобразований их можно привести к стандартному виду. Это позволяет изучать форму распределения случайной величины, не отвлекаясь на ее физическую суть.
Одно из наиболее важных в статистике — нормальное распределение, или распределение Гаусса. Оно имеет вид симметричного колокола с тонкими хвостами. Так что в диапазон µ ± 3σ (среднее ± три стандартных отклонения) попадает 99,73% всех измерений. Финансовые модели, основанные на этом свойстве нормального распределения, выглядят обманчиво надежно. А реальность такова, что кризисы случаются существенно чаще… просто потому, что мир финансов основан на распределениях с толстыми хвостами.
Качество шесть сигм
Шесть сигм – концепция управления, разработанная в корпорации Motorola в середине 1980-х. Качество шесть сигм означает, что бизнес-процесс налажен таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазоне µ ± 6σ, всё еще удовлетворяет требованиям (допускам). Это достигается за счет уменьшения рассеяния. На графике представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества доля брака сокращается. Помните, что границы заданы извне, а кривая построена на основе измерений.
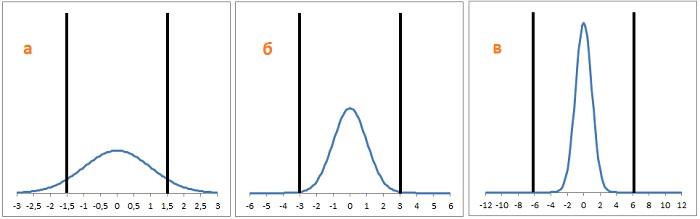
Качество, измеренное в сигмах
(а) в границы допуска попадают значения случайной величины, находящиеся в диапазоне µ ± 1,5σ, за границами остается довольно много значений, и всё это – брак; (б) в границах допуска находится значительно больше измерений: µ ± 3σ, но по-прежнему 6 измерений из 100 относятся к зоне брака; (в) в границах допуска почти все измерения: µ ± 6σ, брак составляет 3 измерения на 1 000 000.
Условная вероятность
Два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. И наоборот. Если вероятность наступления события А будет различной, в зависимости от того, произошло ли событие В, то можно подсчитать условную вероятность:
Р(А|В)
Читается: вероятность события А при условии наступления события В. Понятие условной вероятности является очень важным в теории вероятностей и в жизни. Однако люди плохо оценивают условную вероятность, подменяя ее эвристикой доступности, т.е. интуитивным процессом, в котором вместо частоты события оценивается лёгкость, с которой аналогии всплывают в памяти. Даниел Канеман приводит такой пример.
Некто описывает своего соседа: «Стив очень застенчив и нелюдим, всегда готов помочь, но мало интересуется окружающими и действительностью. Он тихий и аккуратный, любит порядок и систематичность и очень внимателен к деталям». Кем вероятнее работает Стив: фермером или библиотекарем? Все немедленно отмечают сходство Стива с типичным библиотекарем, но почти всегда игнорируют статистику: на каждого мужчину-библиотекаря в США приходится более 20 фермеров.
Закон больших чисел
Чем большее число раз выполнить один и тот же эксперимент, тем ближе среднее значение по выборке будет к истинному среднему генеральной совокупности. Возьмем монету, присвоим орлу значение 1, а решке 0, и покажем, как меняется среднее с увеличением числа бросков:
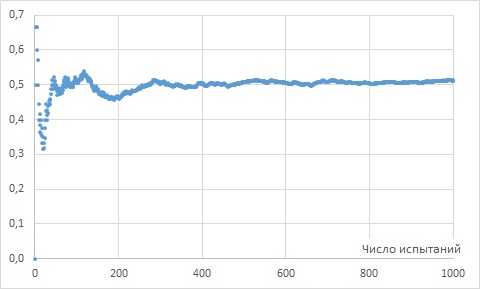
Иллюстрация закона больших чисел: с увеличением числа бросков среднее стремится к 0,5
В повседневной жизни люди строят выводы на основе нескольких, а то и одного прецедента. Даниел Канеман назвал это законом малых чисел, который
…создает чересчур осмысленную картину реальности. Рассматривая событие со статистической точки зрения, мы интересуемся его связью с тем, что могло произойти, а не как именно оно произошло. Никакой особой причины не было, случай выбрал его среди других. Сколько выгодных сделок должен заключить ваш финансовый консультант, прежде чем вы решите, что он необычайно эффективен? Какое количество успешных приобретений убедит совет директоров, что у генерального директора талант к подобным сделкам? Простой ответ на эти вопросы гласит, что, следуя интуиции, вы чаще воспримете случайное событие как закономерное.
Нормальное распределение. Построение графика в Excel. Концепция шести сигм: https://baguzin.ru/wp/?p=1170
Левин, Дэвид М., Стефан, Дэвид, Кребиль, Тимоти С., Беренсон, Марк Л. Статистика для менеджеров с использованием Microsoft Excel, 4-е изд. — М.: Издательский дом «Вильямс», 2004. — 1312 с. Раздел 6.1. Нормальное распределение.
Питер С. Пэнди, Роберт П. Ньюмен, Роланд Р. Кэвенег. Курс на Шесть Сигм. Как General Electric, Motorola и другие ведущие компании мира совершенствуют свое мастерство. – М.: Издательство ЛОРИ, 2002. – 400 с. Конспект: https://baguzin.ru/wp/?p=16912
Питер Панде, Ларри Холп. Что такое «шесть сигм»? Революционный метод управления качеством. – М.: Альпина Бизнес Букс, 2005. – 160 с. Конспект: https://baguzin.ru/wp/?p=2405
Дэниэль Канеман. Думай медленно… решай быстро. – М.: АСТ, 2013. – 656 с. Конспект: https://baguzin.ru/wp/?p=7840