Юрий Адлер. Введение в планирование эксперимента

Когда я учился в школе (1970-е) мои родители работали в НИИ, и слова «планирование эксперимента» я слышал постоянно. Похоже, что эта культура за время новой России утрачена или, как минимум, подзабыта. Предмет редко преподается в вузе, упоминание о нем почти не встретишь в Инете. Это небольшое учебное пособие предназначено для первого знакомства с планированием эксперимента. Оно не требует никаких предварительных знаний о предмете. К сожалению, автор пособия – Юрий Павлович Адлер, гуру менеджмента качества – умер 12 ноября 2020 г.

Юрий Павлович Адлер. Введение в планирование эксперимента. – М.: Изд. дом МИСиС, 2014. – 36 с.

Скачать конспект в формате Word или pdf, примеры в формате Excel

Купить цифровую книгу в ЛитРес

Глава 1. Пробуем приготовить шоколадный напиток

Планирование эксперимента – важный элемент исследований. Благодаря планированию мы сокращаем число опытов и получаем оценку неопределенности результатов, а также возможность их  визуализировать. Последнее способствует обмену мнениями и выдвижению новых гипотез. Это создает систематическую методологию исследования.

Планирование эксперимента отвечает на три вопроса: сколько опытов провести, в каких условиях, в каком порядке. Можно выделить целый ряд практических задач, подразумевающих планирование эксперимента:

• Оценка константы. Скорость звука, постоянная Планка, температура плавления.
• Аппроксимация. Оценка параметров математической модели, градуировка измерительной системы.
• Оптимизация. Нахождение значений переменных, приводящих к оптимуму системы.
• Адаптация. Оптимизация во времени. Определение параметров при изменяющихся внешних условиях, например, при изменении свойств сырья.
• Отсеивание. Выбор из множества возможностей одной или нескольких, наиболее полно соответствующих набору критериев. Выбор катализатора, растворителя, добавки.
• Дискриминация. Отсеивание не на множестве объектов, а па множестве моделей. Надо найти модель, наилучшим образом согласующуюся с результатами эксперимента.

Успех планирования эксперимента зависит от априорных знаний о предмете исследования. Используем поиск рецепта приготовления горячего жидкого шоколада в качестве сквозного примера. Априорная информация гласит, что предпочтения потребителя зависят от шести переменных, которые в планировании эксперимента принято называть факторами:

1. доля шоколада;
2. сливочность (отношение молоко/сливки);
3. консистенция (густота);
4. температура напитка;
5. сладость (связана с долей шоколада);
6. интенсивность (уровень) чувства голода.

Исследования показали, что существует оптимальное соотношение какао (шоколада) и сахара, поэтому они не рассматриваются в данной работе как независимые факторы. Значит, фактор 5 учитывается как фиксированное значение (уровень) для соответствующего уровня фактора 1 и в нашем исследовании не участвует. Таким образом факторы 1, 2, 3 дают рецепт напитка, а 4 и 6 – это условия внешней среды. О температуре известно, что ее оптимум соответствует 66…77 °C для любых горячих напитков. Поскольку голод влияет на степень удовлетворенности потребителя любой пищи, поэтому пробы надо проводить в одно и то же время или при одном и том же уровне голода, иначе результаты будет трудно сравнивать. Мы также знаем, что один человек в короткое время не может сравнить более 5–6 вариантов. Благодаря априорным знаниям нам удалось свести задачу с шестью факторами всего к трем.

Современный подход к планированию позволяет проводить опыты так, чтобы одновременно изменялись уровни всех факторов. Последующий анализ даст возможность рассматривать каждый фактор отдельно. Это повышает эффективность экспериментов и их точность. Можно было бы зафиксировать сливки и консистенцию, и менять только уровень шоколада. Найдя наилучший уровень шоколада, и зафиксировав его, можно было бы менять уровень сливок, сохраняя постоянной консистенцию. И действовать так, пока не кончатся рассматриваемые факторы. Такой эксперимент принято называть однофакторным.

Приступим к построению программы эксперимента. Смеси будем делать с разными уровнями какао (и сахара), сливок, консистенции (объема сгустителя). Были определены диапазоны уровней для каждого ингредиента, которые затем разбили на 11 категорий:

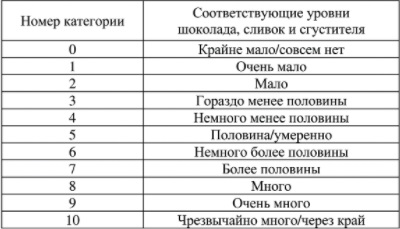
Рис. 1. Уровни для ингредиентов горячего жидкого шоколада

Степень удовлетворенности потребителя оценивалась по субъективной стобалльной шкале.

Поскольку с чего-то надо начать, наша команда за точку отсчета приняла смесь, соответствующую 5-й категории для сливок и шоколада и 3-й категории – для консистенции. Для сравнения разных вариантов удобнее рассматривать уровни ингредиентов, расположенные симметрично относительно этой центральной точки. Чем большее влияние фактора мы ожидаем, тем меньший шаг его изменения следует взять. Формируя первую серию экспериментов, мы решили отступить от среднего значения на два уровня:

Рис. 2. Факторы и их уровни для первой серии экспериментов с жидким шоколадом

Переберем три фактора на двух уровнях каждый (8 вариантов), плюс исходная точка. Результаты девяти дегустаций:

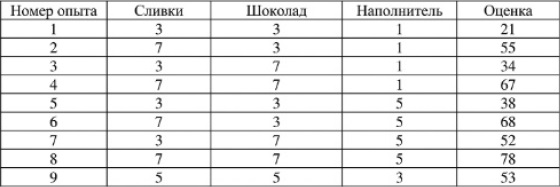
Рис. 3. План первой серии экспериментов и ее результаты

Наши исходные гипотезы не выдержали проверки. Предпочтение было отдано смесям с большим содержанием ингредиентов (№ 8). Примем восьмую смесь за новую точку отсчета, и во второй серии экспериментов будем «плясать» от нее, причем уменьшим шаг до одной категории:

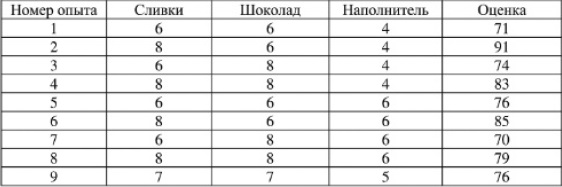
Рис. 4. План и результаты второй серии экспериментов

Победила смесь номер 2, а кучность результатов возросла. Получается, что рецепт требует много сливок, умеренное количество шоколада и среднюю консистенцию. Обратите внимание, нам потребовалось 18 экспериментов. Если бы вы захотели перебрать все 11 градаций для каждого из трех факторов, то вам потребовалось бы проделать 3¹¹ = 177 147 различных опытов!

2. Учимся считать

Изучим математический аппарат, лежащий в основе планирования эксперимента. Факторы принято обозначать заглавными или строчными латинскими буквами х с индексами. В примере с шоколадом обозначим сливки через х₁, шоколад – х₂ и наполнитель – х₃. А вместо номеров уровней этих факторов, используют обозначения: 0, +1 и -1. Такие обозначения называют «кодированными»:

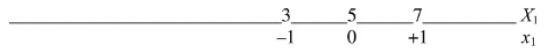
Рис. 5. Кодирование уровней факторов

Над осью указаны физические значения фактора, а под осью – кодированные. Использование кодированных переменных создает огромные преимущества при расчетах. После кодирования факторы и их уровни для первой серии экспериментов с шоколадом приобретут вид (сравни с рис. 2):

Рис. 6. Кодированные факторы и их уровни

Схема кодирования преобразует шкалы факторов так, чтобы расстояния от нулевой точки до любого уровня (верхнего или нижнего) было одинаковым для всех факторов. Благодаря этому для трех факторов координаты точек, в которых мы будем проводить опыты, соответствуют вершинам куба:

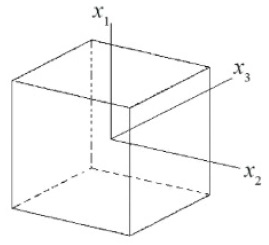
Рис. 7. Факторы в пространстве

После кодирования план первой серии экспериментов и его результаты примут вид:

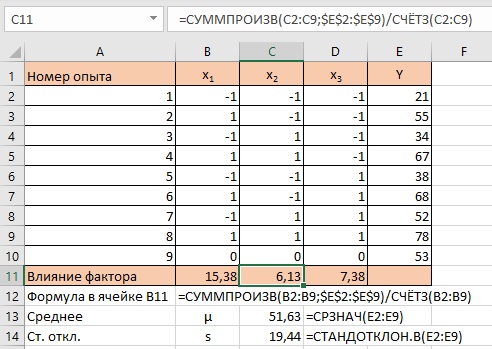
Рис. 8. План и результаты первой серии экспериментов

Y используется для обозначения результатов опытов. Их принято называть «откликами». Теперь можно выяснить, как влияют на отклик все факторы в отдельности, и наблюдаются ли совместные эффекты факторов. Для начала оставим в стороне девятый опыт, и представим, что факторы на результат не влияют. Тогда различия в откликах обусловлены только естественной вариабельностью системы. Для восьми опытов определим средний отклик и стандартное отклонение: μ = 51,63, s = 19,44. Если бы вариации не было, то стандартное отклонение было бы близким к нулю. Столь значительная вариации говорит, что за ней может скрываться влияние факторов.

Рональд Фишер, создатель концепции планирования экспериментов, назвал это «информационным количеством». Если эффект фактора оказывается существенным, его можно «вычесть» из общего информационного количества. Оно тогда уменьшится, и в нем останется меньше возможностей для обнаружения других эффектов. Так постепенно можно выделить все важные эффекты. То, что останется – будет «шумом». Шум характеризует естественную вариацию отклика при «одинаковых» условиях проведения опытов.

Чтобы оценить вклад факторов в информационное количество нужно найти сумму произведений откликов и значений фактора (вот где полезно, примененное нами кодирование ±1). Если поделить эту сумму произведений на число опытов, получим величину, называемую эффектом фактора х_i (на рис. 8 показаны в ячейках В11:D11 для факторов х₁, х₂, х₃). Мы видим, что вклад всех трех факторов положителен. Это означает, что от нулевого уровня надо двигаться в сторону увеличения значений факторов для нахождения оптимума.

Важное замечание. План первой серии экспериментов предполагал, что факторы связаны с откликом неким уравнением. Мы не знаем каким, но надеемся, что линейным:

или

Вообще, уравнения нужны для того, чтобы предсказывать результаты опытов, которые не были проведены. Но сначала интересно выяснить, как они справляются с предсказанием тех результатов, которые у нас уже есть:

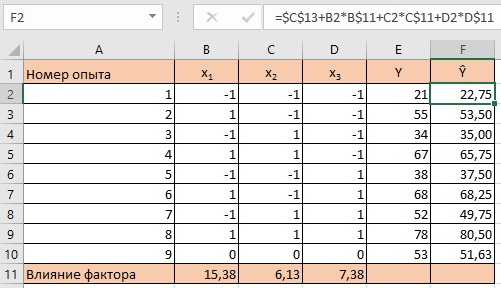
Рис. 9. План и результаты первой серии экспериментов и предсказанные отклики

Знак «крышечка» используется чтобы отличить предсказанные значения отклика от экспериментальных данных. Важно подчеркнуть, что мы подставили кодированные значения факторов. При подстановке натуральных значений (от 0 до 10) все нарушится. Вообще, только коэффициенты уравнения, полученного для кодированных переменных, имеют физический смысл и их можно интерпретировать независимо друг от друга. Наш план эксперимента устроен так, что обладает свойством независимой оценки роли факторов. Математики называют это свойство плана – «ортогональностью».

Теперь, когда мы вычислили коэффициенты уравнения плоскости и сделали предсказания для экспериментальных точек, возникает вопрос: хорошо ли предсказывает наше уравнение, значение отклика или плохо? Ясно, что уравнением плоскости нельзя описать все процессы, какие только есть на свете. Бывают и другие поверхности и соответствующие им уравнения. Нужна какая-то мера «качества» соответствия. Первое, что приходит в голову, – это требование абсолютно точного соответствия фактических и предсказанных значений.

Однако, воспользоваться этим критерием нельзя. В XIX в. немецкий математик Карл Вейерштрасс сформулировал теорему. Ее смысл заключается в том, что если есть в пространстве некоторой размерности определенное множество несовпадающих точек, то всегда существует полином, степень которого не выше, чем число точек минус единица, причем такой, что он пройдет в точности через каждую точку. Выходит, что достаточно взять в полиноме не четыре коэффициента, а восемь, как все экспериментальные точки обязательно совпадут с расчетными. Когда вид уравнения известен заранее, можно говорить об изучении разностей двух последних столбцов таблицы на рис. 9, которые принято называть «остатками». Но и тогда нужен некоторый «эталон сравнения». Наша ситуация сложнее: мы не знаем ни «правильного» уравнения, ни эталона. Приходится двигаться последовательно. Сначала мы предполагаем, что уравнение задано. Например, что это то уравнение, которое мы построили. Тогда попытаемся подыскать эталон для его остатков.

Сначала вычислим квадраты остатков:

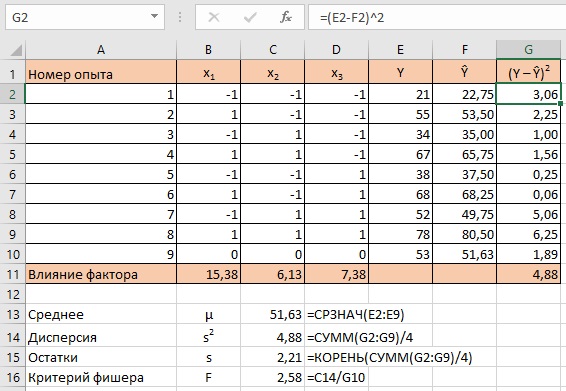
Рис. 10. Предсказанные значения и квадраты остатков

Остаточная дисперсия s² выборки равна сумме квадратов остатков, деленной на число степеней свободы df. df = число опытов минус число коэффициентов в уравнении = 8 – 4 = 4. s² = 4,88 а s = 2,21.

Обратите внимание, насколько эти остатки меньше первоначального значения стандартного отклонения в предположении, что вся изменчивость отклика является случайной. Тогда s равнялось 19,44. Это означает, что наше уравнение лучше описывает точки, чем гипотеза, предполагающая, что факторы не оказывают влияния на отклик.

Но насколько уравнение лучше? Для ответа на этот вопрос мы и припасли опыт в нулевой точке. В ней квадрат отклонения равен 1,89. А отношение дисперсий s² для восьми точек и для нулевой точки в статистике называется критерием Фишера F = 4,88/1,89 = 2,58. Много это или мало? Пока мы не можем ничего сказать о критерии Фишера: слишком мало данных.

3. Экономим опыты

Вернемся к эксперименту с шоколадом, и покажем прямую дорогу от результатов первой серии опытов к оптимальной смеси. Это направление называется направлением градиента, а движение в этом направлении – движением по градиенту. Источником информации о направлении градиента служит уравнение (2). Это линейное уравнение плоскости в четырехмерном пространстве:

Повторим таблицу на рис. 8. В ней условия опытов принято записывать в кодированном виде, а вот вычисления направления градиента и условий опытов, которые ему соответствуют, удобнее вести снова в натуральных значениях факторов (см. рис. 11).

Свободный член не участвует в вычислении градиента. Коэффициенты при значениях факторов – тангенс угла наклона плоскости к соответствующей координатной оси. Если тангенс угла наклона умножить на интервал варьирования, который одновременно служит прилежащим катетом прямоугольного треугольника, то получится противолежащий катет. А его верхняя точка как раз и будет лежать на градиенте. Если проделать эту операцию со всеми тремя факторами, то получится строка: 30,75; 12,25; 14,75.

Точка с такими координатами принадлежит градиенту, но находится далеко от рабочей области. Разделим эти координаты на некое число, чтобы вернуться в область исследования, например, на 60. Результат показан в строке «Шаги». Выбор делителя произволен, но не влияет на результаты. Надо просто найти точки на градиенте внутри куба и в его окрестности. Ставить дополнительные опыты внутри куба вряд ли имеет смысл. Там мы и так все знаем. А за границами куба на градиенте лежат точки, часть из которых стоит реализовать в эксперименте. Благодаря такому эксперименту мы надеемся найти наилучшее возможное значение отклика.

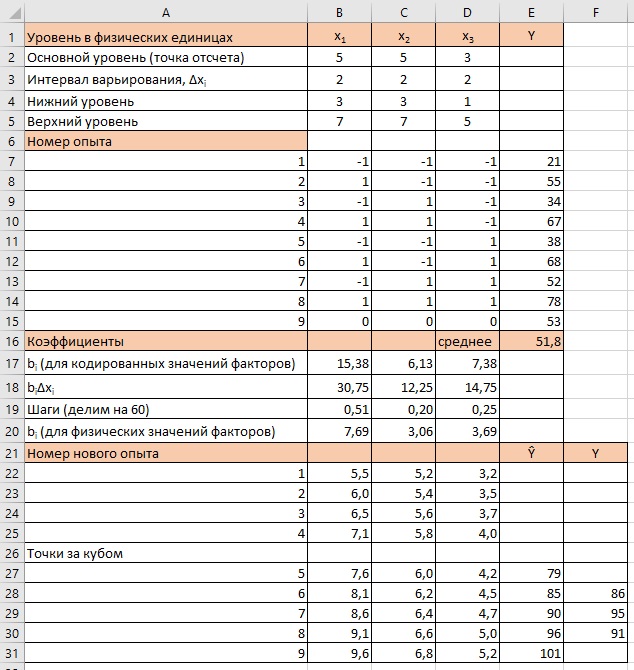
Рис. 11. Расчет градиента (формулы см. в прикрепленном файле Excel

Мы последовательно прибавляем шаги к значениям факторов в нулевом опыте. На рис.11 приведены девять мысленных опытов, причем первые четыре – внутри куба, а остальные пять – за его границами. И для них по нашему уравнению вычислены предсказанные значения Ŷ. В первой части заметки для нахождения оптимума мы провели вторую серию опытов. А здесь надеемся обойтись 2–3 экспериментами.

Реализуем, например, опыты 6, 7 и 8. В нашем случае задача усложняется тем, что дробные доли трудно реализовать. Это снизит точность опытов. Мы получили следующие результаты: 86; 95; 91. Оптимум – 8,6 сливок, 6,4 шоколада и 4,7 наполнителя – похож на результат, полученный в первом разделе, но достигнут быстрее. Это и демонстрирует силу планирования эксперимента и оправдывает усилия, связанные с овладением этой техникой.

4. Даешь подробности!

А нельзя ли еще сократить число опытов? Иногда можно. Для этого рассмотрим дробный факторный эксперимент. Вспомним, что число степеней свободы df равнялось 4. Это было связано с тем, что экспериментов 8, а коэффициентов 4.

Для начала упростим задачу. Допустим у нас только два фактора, тогда нам достаточно провести 4 эксперимента:

Рис. 12. Условия первой серии опытов для плана с двумя факторами

По результатам этих четырех опытов можно найти уравнение плоскости в трехмерном пространстве, в котором три неизвестных: свободный член и два коэффициента при факторах. Значит, у нас есть одна степень свободы! Как ее можно использовать? Можно, например, найти коэффициент, характеризующий взаимодействие между двумя нашими факторами. Его называют эффектом взаимодействия двух факторов или взаимодействием первого порядка. Если такой коэффициент статистически значим, т.е. не случайно отличается от нуля, то зависимость между нашими факторами описывается уже не уравнением плоскости, а более сложным неполным квадратным уравнением.

Итак, мы добавляем столбец с взаимодействием двух факторов. Столбец парного взаимодействия получается перемножением х₁х₂ = х₁*х₂.

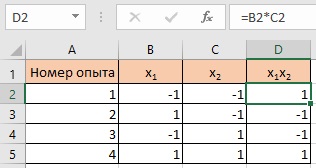
Рис. 13. План для двух факторов со столбцом парного взаимодействия

Но зачем нам уравнение второй степени, если мы заранее знаем, что наша зависимость хорошо описывается уравнением плоскости!? «Лишнюю» степень свободы можно использовать гораздо лучше – для подстановки х₁х₂ = х₃. Давайте найдем строки, представленные на рис. 13 в результатах опытов, представленных в таблице на рис. 10:

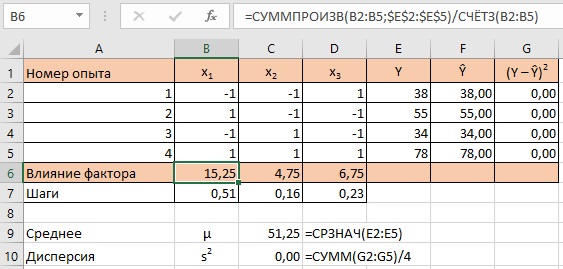
Рис. 14. Дробный факторный эксперимент для трех факторов с четырьмя опытами

В таблице на рис. 10 это опыты с номерами 5, 2, 3, 8. Данные на рис. 14 приводят к уравнению:

Поскольку число степеней свободы df теперь равно нулю, то и остатков регрессии нет. Найденная плоскость в четырехмерном пространстве в точности проходит через наши точки.

Как убедиться, что направление нового градиента мало отличаться от полученного нами ранее? Найдем точки, которые лежат на направлении нового градиента и сравним их с теми, что мы нашли раньше по полному факторному плану из рис. 11. Там для первого, второго и третьего факторов, пропорция была 0,51; 0,20; 0,25 (см. строку «Шаги»). Если теперь мы проделаем то же самое с нашим новым уравнением, то получим 0,51; 0,16; 0,23. В пределах точности нашего эксперимента получилось практически то же самое направление градиента. А опытов теперь меньше!

К сожалению, в реальной жизни существует масса препятствий, которые не гарантируют успех такой экономии. Но регулярная процедура, описанная в предыдущих главах, практически гарантирована. У нас здесь слишком мало факторов, чтобы рассчитывать на большую экономию числа опытов.

Надеюсь, что теперь вы готовы самостоятельно решать простые задачи и читать специальные учебники и публикации.

Библиография

Hoerl R.W., Snee R.D. Statistical Thinking: Improving Business Performance. – Duxbury: Thomson Learning. – Australia, Canada, a.o., 2002.-526 p. (P. 288-291).

Налимов В.В. Теория эксперимента. – М.: Наука, 1971. – 208 с.

Адлер Ю.П. Введение в планирование эксперимента. – М.: Металлургия, 1969. – 158 с.

Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование экспериментов при поиске оптимальных условий. – М.: Наука, 1976.

Адлер Ю.П. Предпланирование эксперимента. – М.: Знание, 1978. – 72 с.

Fisher R.A. The Design of Experiments. – Edinburgh: Oliver and Boyd, 1935.