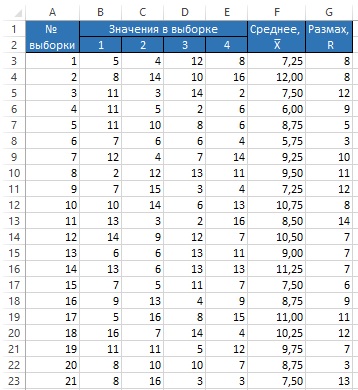
В настоящей заметке представлены удобные шаблоны в Excel для построения контрольных карт Шухарта. Если эта тема для вас новая, предлагаю начать с книги Д. Уилер, Д. Чамберс. Статистическое управление процессами. Существует много видов контрольных карт (см., например, ГОСТ Р 50779.42-99. Статистические методы. Контрольные карты Шухарта). Но основных – два: карта средних и индивидуальных значений. Если контролируемый процесс устроен так, что некоторые значения образуют естественные группы, то рекомендуется использовать контрольную карту средних. Исходные данные следует собрать в группы, рассчитав для каждой из них среднее значение и размах (размах – разность между максимальным и минимальным значением в группе; рис. 1).
Рис. 1. Исходные данные для построения карты среднего и размаха
Скачать заметку в формате Word или pdf, примеры в формате Excel
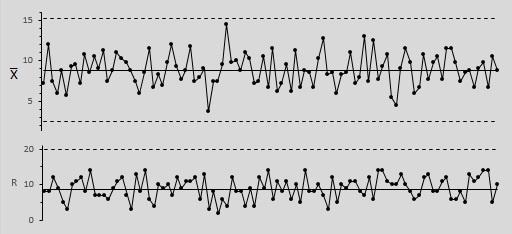
Рекомендуется накопить 20–30 средних значений, и уже по ним строить карту. Карта среднего и размаха содержит два графика (рис. 2), на верхнем – карта среднего, на нижнем – карта размаха. На карте среднего отображают средние значения отдельных групп, а также три линии: центральную (среднее средних) и две контрольные границы – верхнюю и нижнюю. Если в контексте данных отрицательные значения не имеют смысла (например, анализируются проценты), а расчетное значение для нижней границы меньше нуля, эту границу, либо не наносят на карту, либо проводят на отметке ноль. На карте размаха наносят средний размах, верхнюю и нижнюю контрольные границы. Здесь нижняя контрольная граница всегда неотрицательна, а присутствует она для n ≥ 7 (при меньших n коэффициент D3 равен нулю).
Границы рассчитывают по следующим формулам:
UCLX̅ = X̿ + A2R̅ – верхняя граница карты средних;
CLX̅ = X̿ – центральная линия карты средних;
LCLX̅ = X̿ – A2R̅ – нижняя граница карты средних;
UCLR = D4R̅ – верхняя граница карты размахов;
CLR = R̅ – центральная линия карты размахов;
LCLR = D3R̅ – нижняя граница карты размахов.
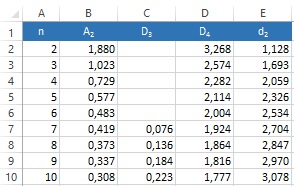
Здесь Х̅ – среднее значение в одной выборке, X̿ – среднее по нескольким значениям средних Х̅, R̅ – среднее по размахам в нескольких выборках, A2, D3, D4 – коэффициенты, зависящие от размера выборок n (рис. 3). При построении карты на рис. 2 использованы 30 первых значений.
Рис. 2. Карта среднего и размаха; значение D3 для n = 4 отсутствует, поэтому нижней границы на карте размаха нет
Рис. 3. Константы для контрольных карт среднего и размаха (A2, D3, D4) и индивидуальных значений (d2)
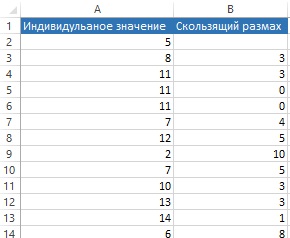
Если данные образуют некий ряд, не подлежащий группировке, применяются карты индивидуальных значений и скользящего размаха. Они получили название XmR-карт. Скользящий размах есть модуль разности последовательных значений (рис. 4; использованы данные из столбца В на рис. 1).
Рис. 4. Исходные данные для построения XmR-карты
Для XmR-карты границы рассчитывают по следующим формулам:

нижняя граница карты размахов отсутствует.
Здесь ![]() – средний скользящий размах, а значения коэффициентов d2 и D4 берутся для n = 2 (см рис. 3). Почему так? Потому что карта скользящего размаха фактически использует группы из двух последовательных измерений для вычисления размаха. Для расчета всех линий использованы первые 30 значений.
– средний скользящий размах, а значения коэффициентов d2 и D4 берутся для n = 2 (см рис. 3). Почему так? Потому что карта скользящего размаха фактически использует группы из двух последовательных измерений для вычисления размаха. Для расчета всех линий использованы первые 30 значений.
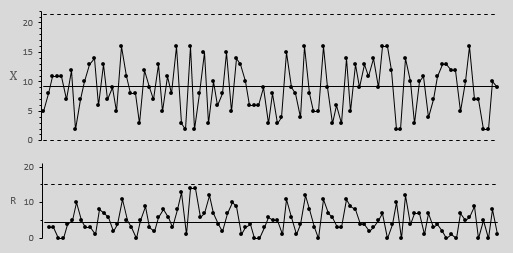
Рис. 5. XmR-карта индивидуальных значений и скользящего размаха
Если сравнить карту средних (рис. 2) и индивидуальных значений (рис. 5), видно, что последняя обладает большей волатильностью, и диапазон между нижней и верхней контрольными границами шире. Это не удивительно, так как на карте средних используется усреднение по четырем значениям. Если выполнить усреднение по еще большему числу значений, границы станут еще ближе.
Важным моментом при построении контрольных карт является использование двух статистик: средних и размахов. Часто используемый неверный способ расчета контрольных границ заключается в том, что используется лишь одна статистика. Например, при построении карты как на рис. 5, использовались бы только индивидуальные значения и их дисперсия. В этом случаев границы рассчитывались бы по следующим формулам:

Поскольку при таком подходе используется единая статистика рассеяния, карты размахов в данном случае нет. Вычисление контрольных пределов, основанное на использовании единой статистики рассеяния, приведет к неправильному результату. Подобные вычисления приводят к расширению полосы между контрольными пределами. Правильный путь вычисления контрольных пределов для карты индивидуальных значений всегда должен использовать двухточечные скользящие размахи.
Эта заметка была полностью переработана в октябре 2016 г. Оказалось, что в первоначальном варианте я предлагал неверное решение. С первоначальным вариантом, представляющим лишь исторический интерес, можно ознакомиться здесь.
Возможно вас также заинтересует:
Контрольные карты Шухарта. Правила определения отсутствия управляемости
Рациональная группировка данных при построении контрольной карты Шухарта
Большое спасибо за публикацию. На вашем примере быстро построила свои карты, хотя теорию до этого читала долго и мучительно. Пишите учебники:)
Спасибо, Светлана. Уже начал писать «Современный управленческий учет» (см. соответствующий раздел меню сайта). Наверное, следующим будет учебник по инструментам менеджмента качества…
Есть замечание: при построении контрольных карт Шухарта нужно использовать другие параметры, а не среднее и дисперсию.
Сигма, которую мы видим — это не среднеквадратичное отклонение.
http://habrahabr.ru/post/139596/
http://habrahabr.ru/post/136193/
http://www.stabbs.ru/download/gost_r_50779.42-99-SPC.pdf
Андрей, возможно, я чего-то не понял в Вашем замечании… но среднеквадратичное отклонение и стандартное отклонение (сигма) это синонимы. См., например, Википедию. В книге Д. Уилер, Д. Чамберс «Статистическое управление процессами» довольно много разнообразных правил построения контрольных карт. Я использую одно из них. В какой-то мере, я согласен, что мои построения не слишком строгие, и, возможно, не соответствуют приведенному Вами ГОСТу, но… Шухарт вкладывал именно экономический смысл в определение границ. В этом я ему не противоречу 🙂
Спасибо, ваш сайт просто кладезь полезной информации.
«Важно подчеркнуть, что Шухарт не вкладывал в квадратичные ошибки («сигмы») никакого статистического смысла. Это вовсе не оценки случайных величин. Это детерминированные константы, вычисленные таким способом, который провоцирует мысль об их статистической природе.»
Адлер Ю. П., Методы Менеджмента Качества №6, 2012 г.
Алексей, я читал указанную замечательную статью Юрия Павловича Адлера. В этом месте готов поспорить… Работы Шухарта на русский язык не переводились, а моего английского недостаточно, чтобы читать в оригинале. Но, как я понял Деминга (см., например, Выход из кризиса, глава 11), границы контрольной карты напрямую зависят от среднего размаха изучаемой выборки, т.е., являются не константами, а зависят от анализируемых данных. У Деминга в качестве оценки кучности данных используется размах, но стандартное отклонение однозначно связано с размахом коэффициентами. Поэтому я и считаю, что верхняя и нижняя границы контрольной карты есть функция средней величины и стандартного отклонения (см. рисунок ).
Но в подразделе 3.5 у Уилера и Чамберса говорится, что вместо групповых размахов можно использовать среднеквадратические и как раз стандартные отклонения. Т.е. сигма не приравнена к стандартному отклонению. Как вы и написали — это функция групповых среднего и статистики рассеяния (размаха, стандартного или среднеквадратического отклонения). Т.е. просто вопрос терминологии: если называть сигму стандартным отклонением — будет путаница.
Здравствуйте! я исследую контрольные карты с памятью, КУСУМ, EWMA. у вас есть информация про них?
Настя, рекомендую почитать здесь
можно в Excel создать массивы данных 5000 50000 чисел с нормальным, равномерным и гамма распределениями ?есть функция по созданию любых массивов?
генерация данных
Настя, я подробно описал использование опции Генерация случайных чисел надстройки Пакет анализа в заметке Выборочные распределения
Контрольные карты Шухарта в Excel вот я тоже делал http://vk.com/labcristal
Сергей, спасите.
Ранее, я спокойно, не думая не о чем строил, Карты при помощи показателя d2 (последние формулы). И мне в голову не приходило, что есть другие способы построения.
Объясните, пожалуйста, доступным языком разницу в А2, d2, D2
Вот ссылка, где я услышал о 6 сигмах. По этому принципу и строил все свои Карты — https://www.youtube.com/watch?v=K3Cc71RfXXo
Не могу понять, когда и какой способ нужно выбирать для построения карт: средний чек в день, кол-во посещений на сайте, кол-во негативных отзывов и тд.
Спасите
Владимир, рекомендую прочитать целиком книгу Уилера и Чамберса «Статистическое управление процессами», недавно вышедшую в Альпине вторым тиражом. Или, по крайней мере, конспект этой книги, на который есть ссылка в начале заметки.
Ваша страница мне очень помогла.
Спасибо.
P.S. Исправьте пожалуйста «Индивидульаное» на «Индивидуальное» (на странице и в файле).
Вячеслав, спасибо. Однако… я не нашел ни одного неверного написания слова «индивидуальное»))
Добрый день! мне нужно построить карту Шухарта для индивидуальных измерений, но данные необходимо найти самостоятельно. Буду благодарна за подсказку, какие открытые данные можно этим способом проанализировать (и откуда их лучше взять).
Заранее спасибо!
Софья, в этом и заключается задание, чтобы найти данные самостоятельно)) Например, можно взять разницу между
временем прилета по расписаниюи фактическим…Сергей, спасибо за идею!
Боже, с чего начать, чтобы понять как и для чего нужны эти карты?
Можно построить карты шухарта для гост 2177 фракционный состав
Помогите, пожалуйста, построить карту риска в EXCEL.
Построение контрольных карт в Excel описано также на http://arhiuch.ru
Здравствуйте, Сергей.
Я менеджер по качеству одной частной маленькой компании по производству пластиковых авто компонентов. Я недавно ушёл с одной западной известной автомобильной компании (со сборочного производства) и устроился на новую работу. Естественно в маленькой российской компании технологи и производственники понятия не имеют о таких инструментах качества, как SPC и MSA (только в общих чертах). Поэтому мне пришлось включать опыт и мозги, чтобы с нулевым бюджетом как-то внедрить эти инструменты.
Спасибо Вам за ваш сайт, в частности данный блог. Благодаря последнему смог внедрить в производство control chart, не покупая сторонние программы. На Вашу личную почту я скинул пару шаблонов с Xbar-R и I-MR картами, и вместе с этим хотел только попросить Вас, чтобы Вы, так сказать, проверили мои файлы и формулы в них (взгляд со стороны), а также можете эти файлы опубликовать у себя на сайте (я не против), чтобы другие не мыкались и могли сразу использовать готовые шаблоны.
Спасибо.
Руслан, рад, что мои материалы приносят практическую пользу. Вот ваши файлы: I-MR-chart.xls, Xbar-R chart.
Добрый день! Работаю на фар. предприятии, подскажите какой алгоритм статистической обработки данных лучше подойдет для «Обзоров по качеству продукции». И какие меры принимать, если Ср/Срк <1, точки лежат в пределах спецификации? Помогите построить контрольные карты в XL (упрощенный вариант)
Пределы спецификации (верхний и нижний предел спецификации задан, прописан по ДФУ)
Доброго дня!
Решил спросить Вас по картам Шухарта:
1. Есть ли у Вас внедрения на предприятиях мясопереработки?
2. Можете ли Вы порекомендовать, какие показатели можно отобрать для сбора и последующего анализа производства мясных продуктов? В принципе, для использования описанного Вами метода можно (и нужно) собирать статистические данные о потерях на каждом переделе. Однако некоторые из них в условиях конкретных предприятий собрать затруднительно. Поэтому я и хотел узнать Ваше мнение о том, по каким критериям нужно отбирать параметры для систематического сбора информации по ним.
С уважением, Константин
1. Нет такого опыта.
2. Для предприятий мясопереработки не подскажу.
Сейчас заканчиваю читать книгу Юрия Адлера и Владимира Шпера «Практическое руководство по статистическому управлению процессами» (скоро появится в блоге). Общая рекомендация: следить нужно за параметрами, которые важны для клиентов процесса, ответственных за процесс и руководства компании.
Начните с того, что прочитайте эти 2 книги:
https://nice-books.ru/books/knigi-o-biznese/korporativnaya-kultura-biznes/276297-eliyahu-goldrat-cel-process-nepreryvnogo.html
https://nice-books.ru/books/knigi-o-biznese/upravlenie-podbor-personala/16134-genri-niv-organizaciya-kak-sistema-principy.html
Добрый день!
Подскажите, пожалуйста, по какой формуле рассчитывается коэффициент d2 Рис.3?
Галя, коэффициент d2 рассчитывается с помощью сложной формулы на основе интегралов. Подробнее см. H.L. Harter, Tables of Ranges and Studentized Ranges, Annals of Mathematical Statistics, v. 31, p. 1122–1147, 1960), раздел 2.2. Поэтому коэффициент d2 для использования в контрольных картах Шухарта всегда приводится в таблицах.
Спасибо!
Добрый день!
Подскажите, пожалуйста, какие ограничения накладываются на исходные данные, могут ли быть в подгруппах объем выборки различный, например в одной n=4, в другой — n=5?
Например, идет сигнал от датчика давления каждый час поступает сигнал, например в один час мы получаем 5 сигналов, а во втором 4 сигнала, в какой-то час сигнала нет вообще, как в таком случае группировать данные?
Галя, а вы что измеряете? Число сигналов каждый час, или какую-то метрику самих сигналов?
Датчик измеряет давление в трубе
Тогда, я бы рекомендовал каждый час делать одинаковое число замеров давления, например, 4. И наносить на ККШ среднее давление по этим четырем измерениям.
Например мы в час имеем 5 значений давления, в другой час пришло 6 значения давления, примерно через каждые десять минут приходят значения давления
Мы не можем контролировать датчик, иногда он может по какой-то причине не отправить сигнал, или он не дошел
Если значения приходят с приблизительно равными интервалами времени, лучше использовать XmR-карту. См. текст выше после рис. 3.
Здесь проблема получается в нахождении контрольных границ, при вычислении коэффициентов, так как требуется определенное число n.
Спасибо!
Почитайте внимательно. Для XmR-карты n=2.
Поняла, спасибо!
Здравствуйте! Очень нужна ваша помощь! В лаборатории 2 человека, одна лаборатория, один метод, одно оборудование, одна проба. Нужно построить карту значений для валидации метода. По методике нужно сделать всего 2 испытания одной пробы. Для того, чтобы построить карту для оценки повторяемости получится только 4 точки (2 значения одного оператора и 2 другого)?? Или можно провести анализ, например, по 5 анализов каждому оператору? И будут ли это карты индивидуальных значений Х и Rm? Как будет выглядеть карта, чтобы рассчитать внутрилабораторную претизиозность, если 2 оператора, но проба одна и время одно и оборудование? Помогите, пожалуйста, разобраться!
Доброй ночи! Есть три выборки контроля качества продукци, тоесть три разные серии продукта по 10 проб с каждой по показателю «количественное определение». Нужно построить контрольную карту. Помогите, пожалуйста, какого вида контрольную карту можно построить в таком случае.
Спасибо.
Толково, лучшее, что я нашел.
Возникла необходимость построить X-S карту. Но данные индивидуальные, то есть несгруппированы в количестве 100 измерений.
Насколько я понял, что для такого вида карт обязательно должны быть группы, исходя из числа которых определяются коэффициенты для средней и среднеквадратического отклонения.
Это так или я что-то не понимаю?
Валерий, для несгруппированных данных строят диаграмму среднего и скользящих размахов. XmR-карту. Ее построение описано в заметке. Используются коэффициенты для n = 2.
Спасибо! Я так и думал.
Добрый день, Сергей. Еще раз попрошу вашей помощи, поскольку с картами Шухарта мне раньше не приходилось иметь дело.
Строю X-S карту для 20 подгрупп, в каждой из которых по 5 наблюдений. Но для S-карты для 5 наблюдений в подгруппе отсутствует значение В3, необходимое для нахождения контрольной границы LCL. Как поступать в таком случае?
И еще. Может подскажите мне, где посмотреть пример построения X-S карты.
Заранее вам благодарен.
Валерий, пример такой карты на рис. 2 Размах по определению не может быть отрицательным, и отсутствие D3 означает, что нижней границы, действительно, нет. Можно считать, что она проходит в точке 0, но тогда границы будут отстоять от среднего размаха на разную величину. При больших n нижняя граница лежит выше нуля.
Большое спасибо.
Правда, я строю карту для средних и стандартного отклонения (у вас — вариация). Но, надо понимать, все сказанное справедливо и для стандартного отклонения, а карта — аналогична?
Размах вариации, естественно!
Здравствуйте, подскажите пожалуйста. Мне нужно сделать работу и пункт в ней называется «Совершенствование системы менеджмента качества технологической подготовки производства».
У меня имеется корпусная деталь-кронштейн. В ней я выявила несколько точных размеров по квалитету.И также определила отклонения этих размеров.
И мне нужно это как-то всё совместить с контрольными картами Шухарта, подскажите пожалуйста, как?
С чего нужно начать?
Здравствуйте помогите мне пожалуйста. ни как не могу понять. Не вошли в голову
Большое спасибо!
Очень нравится ваш подход к делу, вы явно технарь по образованию!)))
Многоуважаемый Сергей! Спасибо вам огромное за такой понятный разбор и пример построения.
Два вопроса:
1.Вы производите расчёт средних индивидуальных значений Х только по з0 образцам, почему не берёте больше? и Надо ли всегда брать для расчёта одинаковое кол-во?
2 В расчёте нижнего предела Х (LNPLx) используется коэффициент 0.729 (-0.729R). Что это такое?Заранее благодарна.
Ольга, про 30 первых значений есть упоминание в книге Дональда Уилера и Дэвида Чамберса Статистическое управление процессами. В ГОСТах я не встречал такого ограничения. В разных экспериментах можно использовать разное число точек для расчета границ. 0,729 — это коэффициент А2 для выборок n = 4.
Сергей, здравствуйте! спасибо Вам огромное за Вашу помощь и консультацию. Подскажите, пожалуйста, если пределы допустимых значений для исследуемых показателей (например рН) оказываются на диаграмме ниже рассчитанной верхней границы (UNPLx) средних значений или выше нижней границы (LNPLx), но при этом точки диаграммы не выходят за пределы допустимых и рассчитанных значений — как это можно объяснить и почему так получилось? Может быть можно на диаграмме индивидуальных значений не выставлять допустимые пределы по НД?
2. Можно ли строить диаграмму по шести показателям (шесть серий)?
3. Если средние значения диаграммы сливаются (разница 0,0001) со средней линией? Что не так?
Заранее примите нашу огромную благодарность.
Ольга, обращаю ваше внимание, что верхняя и нижняя границы ККШ — линии, построенные на основе экспериментальных данных. А допустимые значения (нормы) — это некая хотелка. Границы ККШ и нормы могут взаимно располагаться как угодно. Если границы ККШ глубоко внутри норм, процесс настроен отлично! Если границы ККШ выходят за нормы, это означает, что точки измерений также будут выходить за нормы, т.е., относиться к «браку». Вы спрашиваете: Как так получилось? Процесс на грани стабильности. Его нужно улучшить, чтобы снизить вариабельность.
2. Шесть точек мало, но с чего-то начинать нужно)) Просто понимайте, что полученные по 6 точкам линии менее надежны. Например, получилось, что границы ККШ внутри допусков. Неплохо! Но не спешите почивать на лаврах. Когда наберете статистику, ситуация может измениться.
3. Увеличьте масштаб по оси ординат. Не показывайте на ККШ нормы (допуски). Если на ККШ только экспериментальные данные и границы ККШ, ничего не сольется))