В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных. [1]
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х1, Х2, …, Xk). [2]
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Виды регрессионных моделей
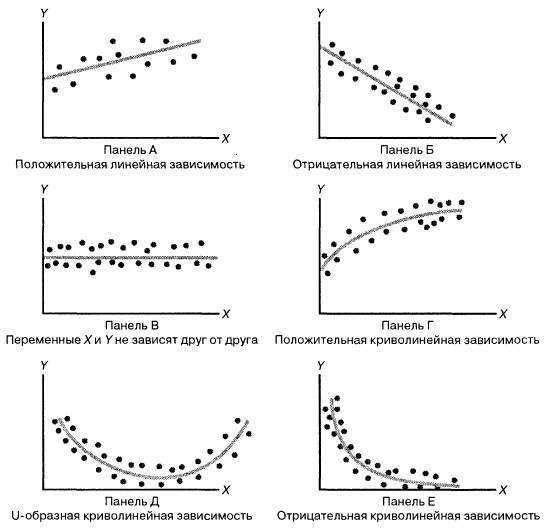
В заметке Представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 1.
Рис. 1. Положительная линейная зависимость
Простая линейная регрессия:
(1) Yi = β0 + β1Xi + εi
где β0 — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β1 — наклон прямой Y, εi— случайная ошибка переменной Y в i-м наблюдении.
В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β0 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2.
Рис. 2. Диаграммы разброса, иллюстрирующие разные виды зависимостей
На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.
Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.
Вывод уравнения простой линейной регрессии
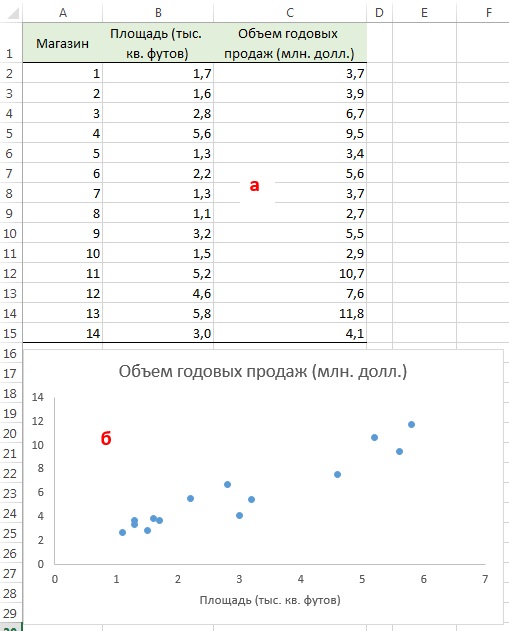
Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (рис. 3).
Рис. 3. Площади и годовые объемы продаж 14 магазинов сети Sunflowers: (а) исходные данные; (б) диаграмма разброса
Анализ рис. 3 показывает, что между площадью магазина X и годовым объемом продаж Y существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследования является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.
Метод наименьших квадратов
Данные, представленные на рис. 1а, получены для случайной выборки магазинов. Если верны некоторые предположения (об этом чуть позже), в качестве оценки параметров генеральной совокупности (β0 и β1) можно использовать сдвиг b0 и наклон b1 прямой Y. Таким образом, уравнение простой линейной регрессии принимает следующий вид:
где ![]() — предсказанное значение переменной Y для i-гo наблюдения, Xi — значение переменной X в i-м наблюдении.
— предсказанное значение переменной Y для i-гo наблюдения, Xi — значение переменной X в i-м наблюдении.
Для того чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии — сдвиг b0 и наклон b1 прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения. Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями Yi, и предсказанными значениями ![]() . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
. Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
Поскольку ![]() = b0 + b1Xi, сумма квадратов принимает следующий вид:
= b0 + b1Xi, сумма квадратов принимает следующий вид:
Параметры b0 и b1 неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b0 и наклона b1 выборки Y. Для того чтобы найти значения параметров b0 и b1, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. При любых других значениях сдвига b0 и наклона b1 сумма квадратов разностей между фактическими значениями переменной Y и ее наблюдаемыми значениями лишь увеличится.
До того, как Excel взял на себя всю рутинную работу, вычисления по методу наименьших квадратов были очень трудоемкими. Excel позволяет решать подобные задачи двумя способами. Во-первых, можно воспользоваться Пакетом анализа (строка Регрессия). Результаты представлены на рис. 4. Во-вторых, можно, выделив точки на графике (как на рис. 3б), кликнуть правой кнопкой мыши и выбрать Добавить линию тренда. Далее можно выбрать вид линии тренда (в нашем случае – Линейная), отформатировать линию, показать на графике уравнение и величину достоверности аппроксимации (R2) (рис. 5).
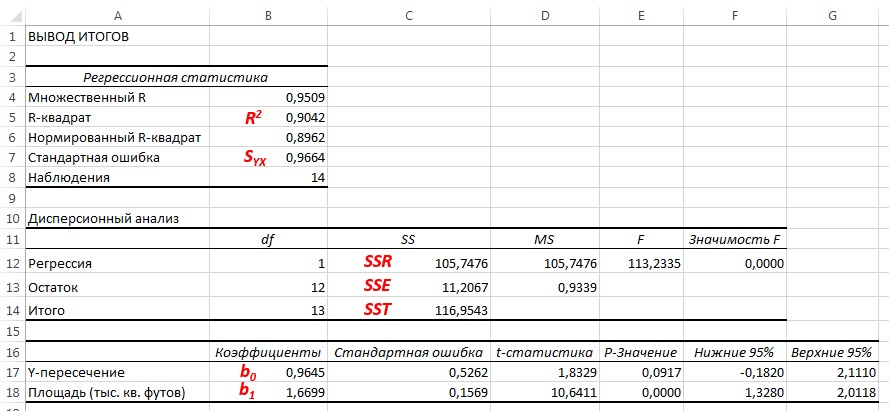
Рис. 4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью Пакета анализа Excel)
Рис. 5. Диаграмма разброса и линия регрессии (тренда) в задаче о выборе магазина
Как следует из рис. 4 и 5, b0 = 0,9645, а b1 = 1,6699. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид: ![]() = 0,9645 + 1,6699Xi. Вычисленный наклон b1 = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b0 = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b0 необходимо относиться внимательно.
= 0,9645 + 1,6699Xi. Вычисленный наклон b1 = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b0 = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b0 необходимо относиться внимательно.
Пример 1. Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: Ŷi = –5,0 + 7Хi. Какой смысл имеют параметры сдвига b0 и наклона b1.
Решение. Сдвиг регрессии b0 равен –5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон b1 равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.
Пример 2. Вернемся к сценарию, изложенному в начале заметки. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров. Предположим, что площадь магазина равна 4000 квадратных футов. Какой среднегодовой объем продаж можно прогнозировать?
Решение. Подставим значение X = 4 (тыс. кв. футов) в уравнение линейной регрессии: ![]() = 0,9645 + 1,6699Xi = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.
= 0,9645 + 1,6699Xi = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала не всегда релевантна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (рис. 3а), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Оценки изменчивости
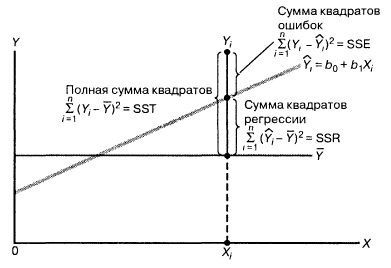
Вычисление сумм квадратов. Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений Yi вокруг среднего значения ![]() . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).
. В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).
Рис. 6. Оценки изменчивости в модели регрессии
Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷi (предсказанным значением переменной Y) и ![]() (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
(средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:
(3) SST = SSR + SSE
Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением:
Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:
Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:
Суммы квадратов, вычисленные с помощью программы Пакета анализа Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 4.
Полная сумма квадратов разностей равна SST = 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR) равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.
Коэффициент смешанной корреляции. Величины SSR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции r2:
Коэффициент смешанной корреляции оценивает долю вариации переменной Y, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476 и SST = 116,9543. Следовательно, r2 = 105,7476 / 116,9543 = 0,904. Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина r2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.
Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен в таблице Регрессионная статистика на рис. 4.
Среднеквадратичная ошибка оценки. Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное ранее, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 5.
Среднеквадратичная ошибка оценки
где Yi — фактическое значение переменной Y при заданном значении Xi, Ŷi — предсказанное значение переменной Y при заданном значении Xi, SSE — сумма квадратов ошибок.
Поскольку SSE = 11,2067, по формуле (8) получаем:
Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл. (т.е. 966 400 долл.). Этот параметр также рассчитывается Пакетом анализа (см. рис. 4). Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная Y. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Cреднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной Y.
Предположения
Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы:
- Ошибка должна иметь нормальное распределение.
- Вариация данных вокруг линии регрессии должна быть постоянной.
- Ошибки должны быть независимыми.
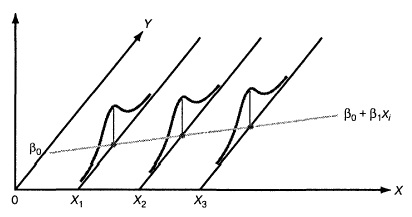
Первое предположение, о нормальном распределении ошибок, требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 7). Как и t— и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.
Рис. 7. Предположение о нормальном распределении ошибок
Второе условие заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (см. рис. 7). Это свойство очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами.
Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.
Анализ остатков
Чуть выше при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.
Оценка пригодности эмпирической модели. Остаток, или оценка ошибки еi, представляет собой разность между наблюдаемым (Yi) и предсказанным (Ŷi) значениями зависимой переменной при заданном значении Xi.
(9) ei = Yi – Ŷi
Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения Xi — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями Xi и остатками еi.
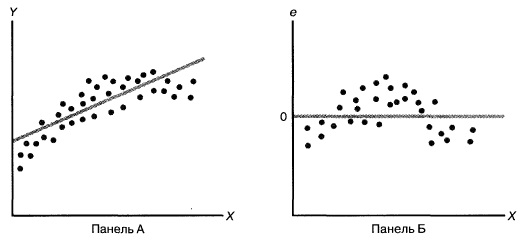
Рассмотрим примеры (рис. 8). Панель А иллюстрирует возрастание переменной Y при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной Y падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными лучше подойдет квадратичная модель. Особенно ярко квадратичная зависимость между величинами Xi и ei проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и Y и выявить недостаточную точность модели простой линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью.
Рис. 8. Исследование эмпирической модели простой линейной регрессии
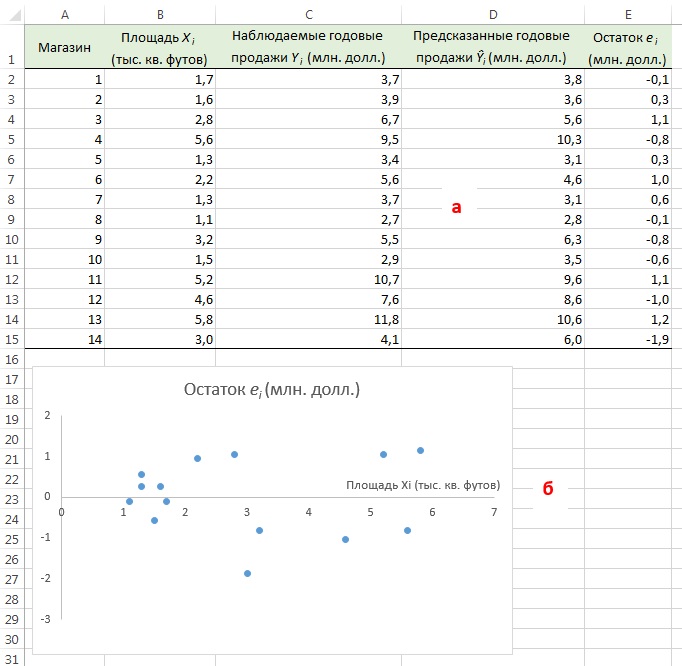
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные и расчеты приведены на рис. 9а (формулы можно посмотреть в Excel-файле). Построим диаграмму разброса, откладывая по вертикальной оси остатки ei, а по горизонтальной — независимую переменную Xi (рис. 9б). Несмотря на большой разброс остатков, между ei и Хi нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.
Рис. 9. Остатки ei, вычисленные при решении задачи о сети магазинов Sunflowers
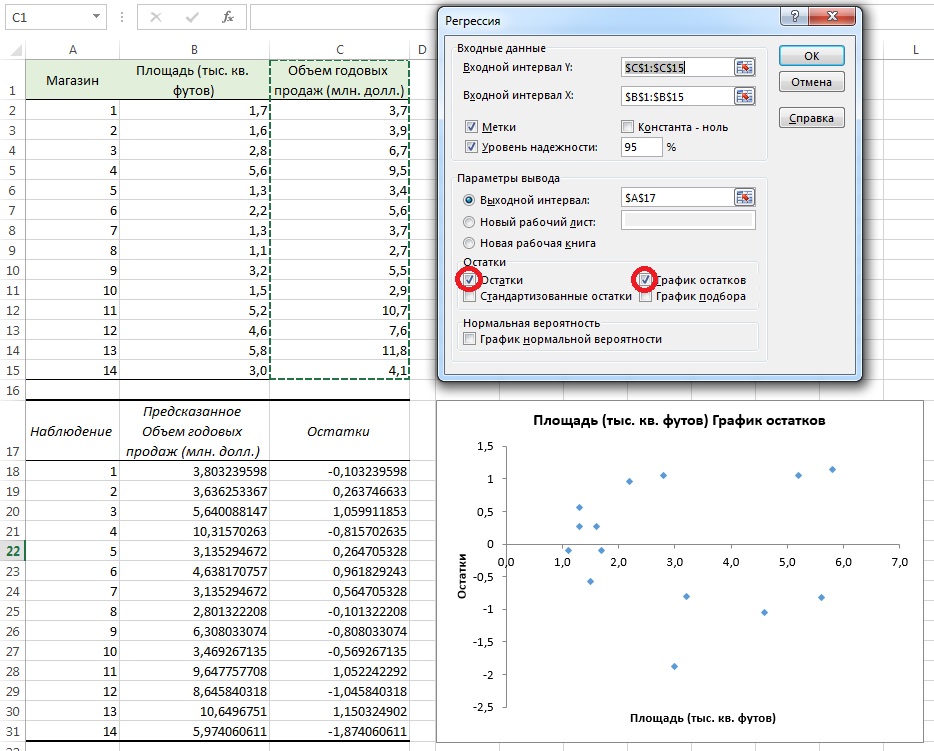
Значения остатков (таблица на рис. 9а) и график остатков (аналог рис. 9б) можно получить непосредственно в процедуре Регрессия Пакета анализа. Просто поставьте соответствующие галки (рис. 10).
Рис. 10. Остатки ei и график остатков полученные с помощью Пакета анализа
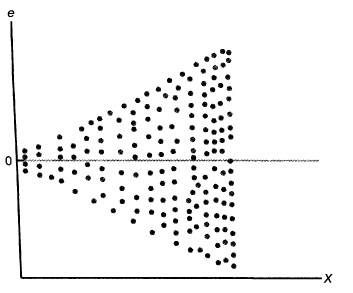
Проверка условий. График остатков позволяет оценить вариации ошибок. На рис. 10 нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы. Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 11). На этом рисунке изображен эффект веера: при возрастании значений Хi ошибки увеличиваются. Таким образом, изменчивость значений Yi при разных значениях Хi является непостоянной.
Рис. 11. Пример нарушения условия независимости вариаций ошибок от Xi
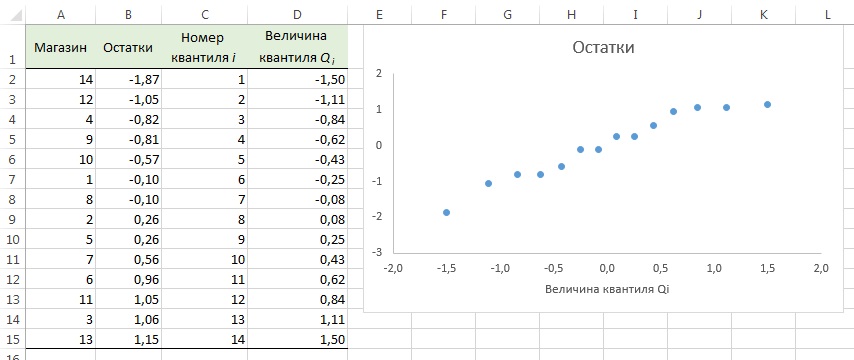
Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим график нормального распределения на основе точечного графика, на вертикальной оси которого отложены значения остатков, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). Для построения такого графика значения остатков должны быть упорядочены по возрастанию (рис. 12). График нормального распределения может быть построен одним кликом с помощью Пакета анализа Excel – просто поставьте соответствующую галочку в окне Регрессия (см. рис. 10, самый низ окна Регрессия – опция График нормальной вероятности).
Рис. 12. График нормального распределения для остатков
Без визуализации данных (с помощью гистограммы, диаграммы «ствол и листья», блочной диаграммы или графика как на рис. 12) проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.
Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независимости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (см. ниже). Если данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени, гипотезу об их независимости проверять не имеет смысла.
Измерение автокорреляции: статистика Дурбина–Уотсона
Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией. Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.
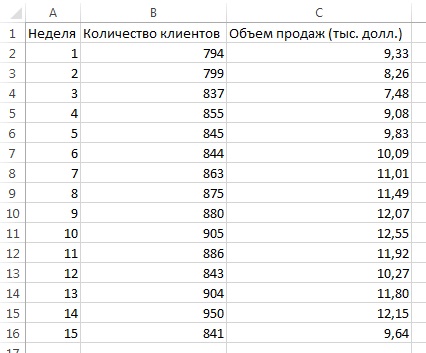
Распознавание автокорреляции с помощью графика остатков. Для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером. Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель (рис. 13).
Рис. 13. Количество клиентов и объемы продаж за 15 недель
Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Построим регрессию с использованием Пакета анализа; включим вывод Остатков, но не будем включать График остатков (рис. 14).
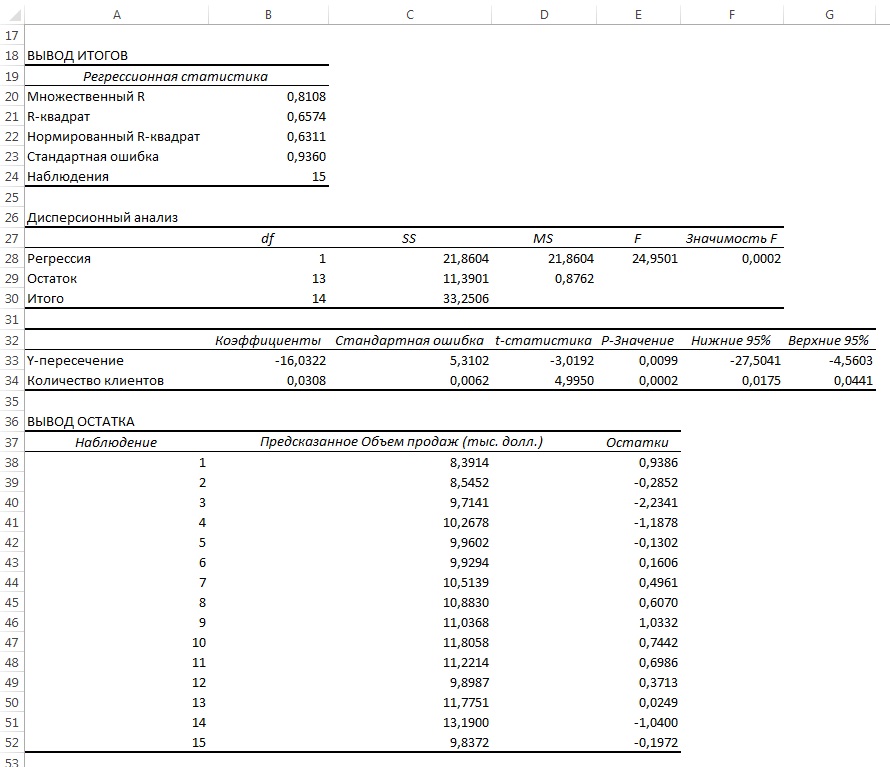
Рис. 14. Параметры линейной регрессии, полученные с использованием Пакета анализа
Анализ рис. 14 показывает, что r2 = 0,657. Это значит, что 65,7% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг b0 переменной Y равен –16,032, а наклон b1 = 0,0308. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 15).
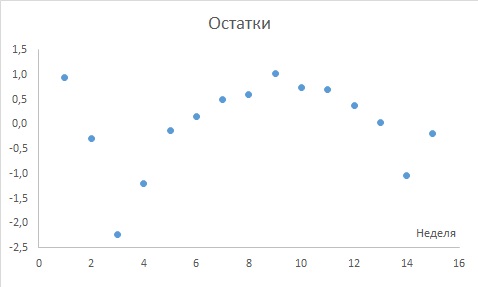
Рис. 15. Зависимость остатков от времени
Анализ рис. 15 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу о независимости остатков следует отклонить.
Статистика Дурбина-Уотсона. Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона. Эта статистика оценивает корреляцию между соседними остатками:
где еi — остаток, соответствующий i-му периоду времени.
Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части. Числитель представляет собой сумму квадратов разностей между соседними остатками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является суммой квадратов остатков. Вот, что по этому поводу написано в Википедии:
где ρ1 – коэффициент автокорреляции; если ρ1 = 0 (нет автокорреляции), D ≈ 2; если ρ1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ1 = -1 (отрицательная автокорреляции), D ≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями dL и dU для заданного числа наблюдений n, числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < dL, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > dU, гипотеза не отвергается (то есть автокорреляция отсутствует); если dL < D < dU, нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с dL и dU сравнивается не сам коэффициент D, а выражение (4 – D).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D = 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (dL и dU), зависящими от числа наблюдений n и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, dL= 1,08 и dU = 1,36. Поскольку D = 0,883 < dL= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t-критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y. Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = 0 (нет линейной зависимости), Н1: β1 ≠ 0 (есть линейная зависимость). По определению t-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11) t = (b1 – β1) / Sb1
где b1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, ![]() , а тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
, а тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t-критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t-критерия, полученные с помощью Пакета анализа Excel
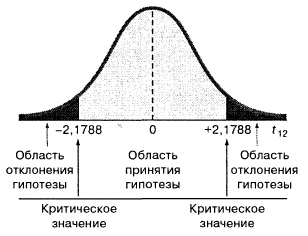
Поскольку число магазинов n = 14 (см. рис.3), критическое значение t-статистики при уровне значимости α = 0,05 можно найти по формуле: tL =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; tU =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t-статистика = 10,64 > tU = 2,1788 (рис. 19), нулевая гипотеза Н0 отклоняется. С другой стороны, р-значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н0 снова отклоняется. Тот факт, что р-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение F-критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. Однофакторный дисперсионный анализ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных k), к дисперсии ошибок (MSE = SYX2).
По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR/MSE, где MSR = SSR / k, MSE = SSE/(n– k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F-распределение с k и n – k – 1 степенями свободы.
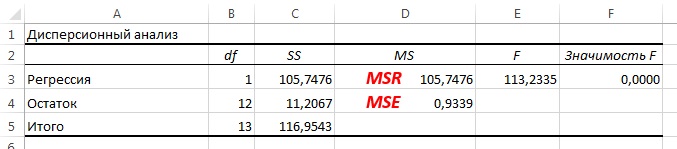
При заданном уровне значимости α решающее правило формулируется так: если F > FU, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t-критерию F-критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F-статистике – на рис. 21.
Рис. 21. Результаты применения F-критерия, полученные с помощью Пакета анализа Excel
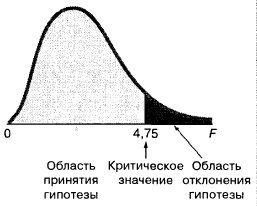
F-статистика равна 113,23, а р-значение близко к нулю (ячейка Значимость F). Если уровень значимости α равен 0,05, определить критическое значение F-распределения с одной и 12 степенями свободы можно по формуле FU =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > FU = 4,7472, причем р-значение близко к 0 < 0,05, нулевая гипотеза Н0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β1. Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β1 и убедиться, что гипотетическое значение β1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β1, является выборочный наклон b1, а его границами — величины b1 ± tn–2Sb1
Как показано на рис. 18, b1 = +1,670, n = 14, Sb1 = 0,157. t12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b1 ± tn–2Sb1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование t-критерия для коэффициента корреляции. Ранее был введен коэффициент корреляции r, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: ρ = 0 (нет корреляции), Н1: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r = +![]() , если b1 > 0, r = –
, если b1 > 0, r = –![]() , если b1 < 0. Тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
, если b1 < 0. Тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
В задаче о сети магазинов Sunflowers r2 = 0,904, а b1— +1,670 (см. рис. 4). Поскольку b1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.
Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов) регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. Ранее для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X:
где 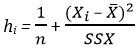 ,
, ![]() = b0 + b1Xi – предсказанное значение переменное Y при X = Xi, SYX – среднеквадратичная ошибка, n – объем выборки, Xi — заданное значение переменной X, µY|X=Xi – математическое ожидание переменной Y при Х = Хi, SSX =
= b0 + b1Xi – предсказанное значение переменное Y при X = Xi, SYX – среднеквадратичная ошибка, n – объем выборки, Xi — заданное значение переменной X, µY|X=Xi – математическое ожидание переменной Y при Х = Хi, SSX = 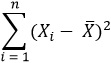
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений Xi. Если значение переменной Y предсказывается для величин X, близких к среднему значению ![]() , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
, доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика YX=Xi при конкретном значении переменной Xi определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
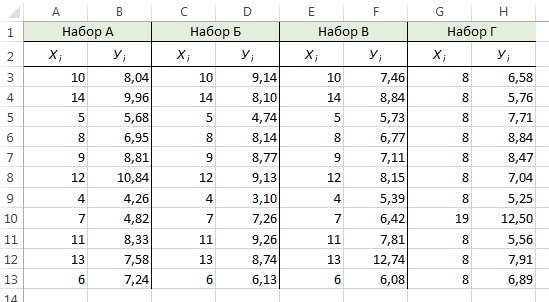
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
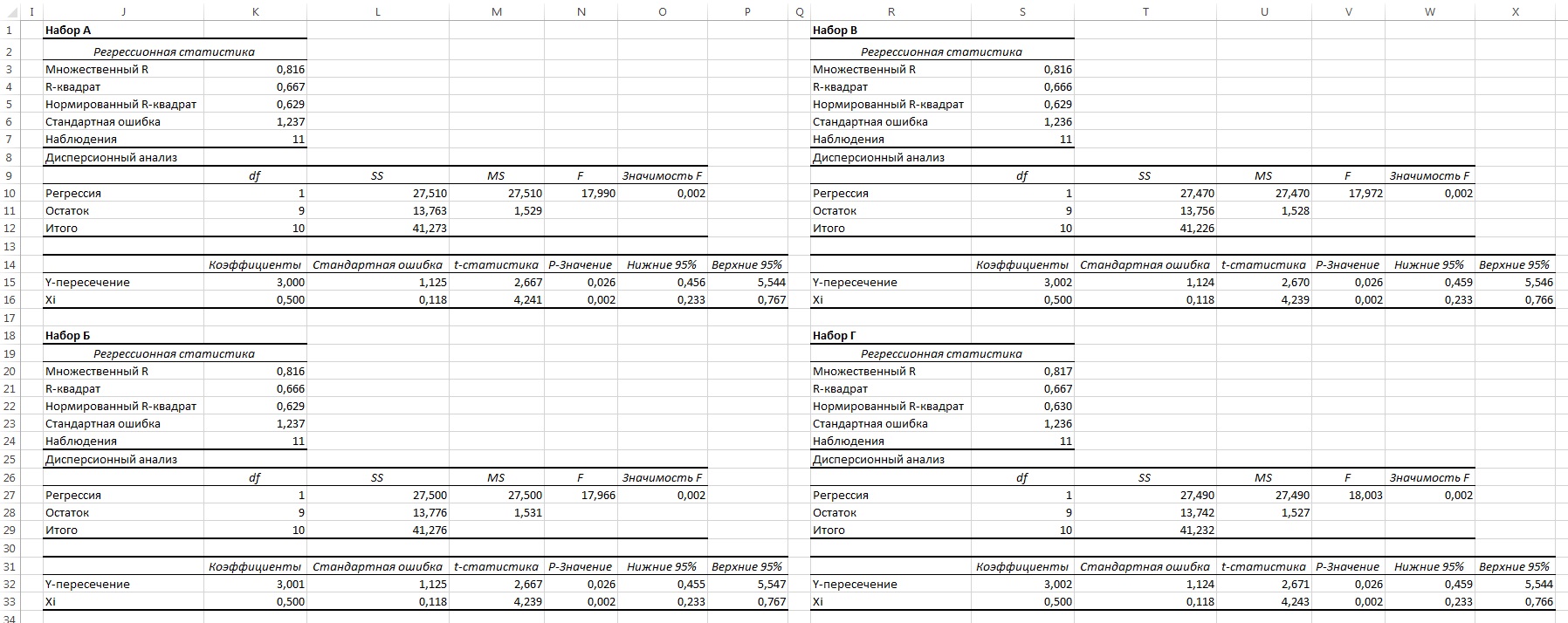
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)
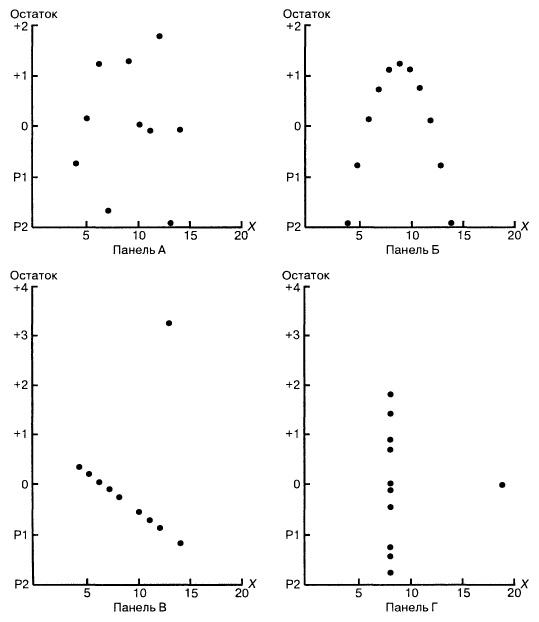
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х8 = 19, Y8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
- Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
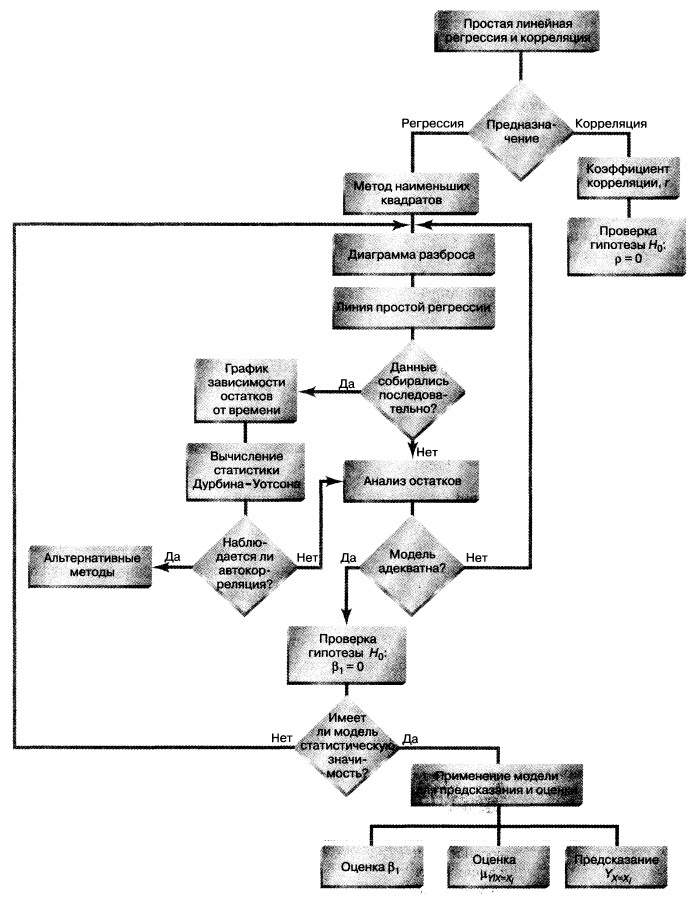
Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Предыдущая заметка Критерий согласия «хи-квадрат»
Следующая заметка Введение в множественную регрессию
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
[2] Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
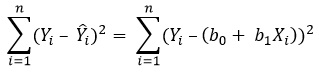


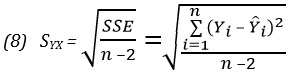
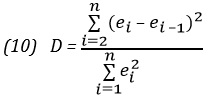
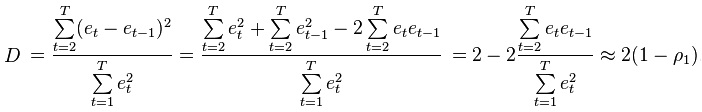










Интересная статья и очень полезный ресурс!
Хочу поделиться полезной программой — надстройка к Excel по выполнению регрессии — http://www.EVArisks.com (все на русском).
Она в автомате не только строит график, но и подбирает лучший тип регрессии (R-квадрат максимальный), а также фильтрует исходную выборку на выбросы значений (иногда на глаз это делать неудобно, да и не всегда очевидно для разных типов регрессии).
Вот видео пример, там за пару кликов очень приличный результат выходит — https://youtu.be/pj928oaWkIo
очень полезные материалы. Спасибо
В тексте вы пишите b0 = 1,6699, а b1 = 0,9645, а на рис.4 все наоборот. Ошибка?
Антон, спасибо. В этом фрагменте содержался целый ряд неточностей. Поправил.
Здравствуйте!
В разделе «Статистика Дурбина-Уотсона» указано, что если D < dL, то присутствует автокорреляция и метод наименьших квадратов применять нельзя. Дайте, пожалуйста совет, как действовать дальше в этом случае. Есть другой метод? Насколько важен уровень значимости 0,05? В моем случае, если взять уровень значимости 0,1, то тогда автокорреляция отсутствует. Насколько это может повлиять на конечный результат?
Максим, регрессионный анализ не чистая математика, но и отчасти искусство. Разные исследователи на одном исходном наборе данных вполне могут прийти к различным зависимостям. Попробуйте провести анализ при уровне значимости 0,1. Постройте диаграмму разброса. Возможно, расположение точек подскажет вам, иной вид зависимости (нелинейный, например, квадратичный). Постройте несколько линий тренда (линейную, степенную, …). Посмотрите, для какой из них значение R-квадрат максимальное. Наконец, проведите
множественную регрессию.Спасибо большое! Мне необходимо было более детально изучить материал по теме,но я не знал, в каком направлении двигаться.
Здравствуйте!
подскажите, пожалуйста, как посчитать максимальную относительную погрешность для регрессионной зависимости?
Гостья, я не могу однозначно понять, что значит «максимальная относительная погрешность для регрессионной зависимости»? Почитайте выше раздел «Оценка изменчивости» (особенно тщательно разберитесь в рис. 6). Могу предположить, что вас интересует величина SSE. А корень из SSE — среднеквадратичное отклонение — σ. Еще есть параметр R2, который характеризует, насколько точно регрессионная кривая (прямая) описывает исходные данные. Чем ближе R2 к единице, тем лучше описывает.
c max относительной погрешностью разобралась. помогите со следующим, поясняю: Я получила некоторые регрессионные зависимости, далее с помощью MATLAB получила уравнение регрессии с коэффициентами, R-квадрат, среднеквадратичной ошибкой уравнения и суммой квадратов остатков. так как я не изучала статистику, теперь у меня возникли сложности с определением критериев Фишера и Стьюдента. подскажите, пожалуйста, формулы для расчета указанных критериев для проверки полученного уравнения регрессии. можно еще и хи-квадрат, заранее благодарна.
По Фишеру рекомендую
Проверка гипотез: двухвыборочные критерии, раздел Использование F-критерия для оценки разности между двумя дисперсиями. По Стьюденту —Построение доверительного интервала для математического ожидания генеральной совокупности. По хи-квадрат —Применение χ2-критерия для проверки гипотезы о равенстве двух или нескольких долейиПрименение χ2-критерия независимости.спасибо
very well;
Подробно и информативно, разобралась с обозначениями элементов регрессии в экселе) Спасибо!
спасибо, великие ) помогли
Добрый день! Спасибо за обсуждение важной темы. Вопрос. Правильно ли я поняла, что если данные собирались не последовательно, например, отбор проб почв в один день, то автокорреляцию остатков модели по критерию Дарбина-Уотсона считать не нужно?
Добрый день! Помогите подобрать уравнение зависимости удорожания работ от исходных данных по работам. Линейная регрессия в excel получается с R2=0.59 и плохими p-значениями для коэффициентов
Большое спасибо! Очень полезно
Добрый вечер.
1. У меня есть следующий вопрос:
если t-критерий меньше 0,05, а F-критерий равен или больше 0,05, то насколько стат значимы такие результаты (при отсутствии авто корреляции)?
2. В статье в пункте «применение t-критерия» при определении гипотез, как я понял, опечатка знака «не равно» нулю.
3. Подскажите, пожалуйста: что делать в случае, если возникнет в разные периоды разная зависимость? (На этапе графического определения вида зависимости)
Выбирать наиболее подходящее уравнение ко всему ряду?
4. Исходя из того, что я читал у меня сложилось впечатление, что множ регрессия может использоваться для определения зависимости, при большем количестве переменных (большем, чем 2). Хотелось бы уточнить: так ли это?
Очень хотелось бы получить ответы на данные вопросы. Заранее спасибо.
1. Для простой регрессии (с одной предсказательной переменной) F-критерий равен квадрату t-критерия. Подробнее см. Конрад Карлберг. Регрессионный анализ в Microsoft Excel. Вы не путаете t-критерий и α-область? Если всё верно, и t-критерий =0,05, то он статистически не значим, так как интегральная вероятность при таком значении t-критерия, например, при 20 степенях свободы = 52% Ее можно найти по формуле в Excel =СТЬЮДЕНТ.РАСП(0,05;20;ИСТИНА). Обычно статистически значимые величины t-критерия <-2 или >2. Подробнее см. t-статистика Стьюдента в Excel.
2. Спасибо. Поправил.
3. Для данных, собранных на протяжении последовательных временных интервалов, используйте анализ временных рядов.
4. Простая регрессия используется для одной независимой переменной и одной зависимой. Множественная регрессия используется для более чем одной независимой переменной и одной зависимой. Подробнее см. Введение в множественную регрессию.
Подскажите, пожалуйста! требуется построить график стандартных ошибок, как это сделать? Я не понимаю, как должен выглядеть так график. ( стандартные ошибки посчитаны)
Вопрос мне не понятен. Стандартная ошибка — это одно значение для выборки. Если у вас несколько выборок и для каждой выборки подсчитана своя стандартная ошибка, то вы можете построить для этих значений любой график. Например, отложив по оси Y значения стандартных ошибок, а по оси Х — номера выборок.
Возможно, вы имеете ввиду график остатков, т.е., отклонение каждой точки в одной выборке от среднего. График остатков можно построить, пройдя по меню: Данные -> Анализ данных (если нужно, предварительно активировав соответствующую надстройку) -> Регрессия. И в открывшемся окне поставить галочку напротив опции «График остатков».
Здравствуйте,подскажите пожалуйста,могу ли я рассчитать критерий Стьюдента для Y и для Х1 и х2?Преподаватель говорит что критерий Стьюдента подходит только для х.Напишите пожалуйста ,как с вами можно связаться7
Екатерина, почитайте t-статистика Стьюдента в Excel. Может быть, найдете ответы на свои вопросы.
Здравствуйте, Сергей !
У Вас в статье есть формула «Среднеквадратичная ошибка оценки», где знаменатель равен (n-2).
В задачах по машинному обучению, которые я сейчас разбираю, используется MSE, что по смыслу вроде бы эквивалентно, но там знаменатель равен (n). Поясните, пожалуйста, этот момент.
Михаил, знаменатель зависит от числа степеней свободы. В общем случае число степеней свободы df = n — k. Здесь n — общее число наблюдений, k — количество параметров, которые оцениваются в модели. Вот что пишет ChatGPT (и я с ним согласен).
Параметры (k) представляют собой количественные характеристики или переменные, которые вы используете для построения модели или оценки статистических параметров. Они могут включать в себя коэффициенты регрессии, средние значения, дисперсии и т.д.
k = 0: В этом случае отсутствуют параметры, оцениваемые в модели. Примером может быть просто вычисление среднего значения для набора данных. df = n — 0 = n.
k = 1: Это может быть случай, когда вы оцениваете один параметр. Например, при проведении t-теста для сравнения средних значений двух групп. В этом случае df = n — 1.
k = 2: Это может быть случай использования регрессии с одной независимой переменной. Каждая независимая переменная добавляет один параметр в модель. Таким образом, если у вас есть две независимые переменные, df = n — 2.
k = 3: Это может быть пример использования анализа дисперсии (ANOVA) с тремя группами. В ANOVA оцениваются средние значения для каждой группы, и df = n — 3.
Обратите внимание, что общее количество наблюдений (n) остается постоянным для данного набора данных, а число степеней свободы (df) зависит от количества параметров (k), которые вы оцениваете в вашей статистической модели.